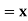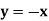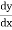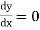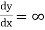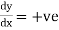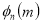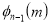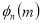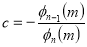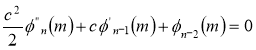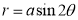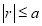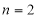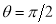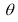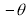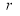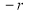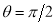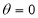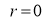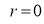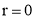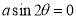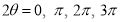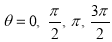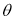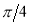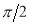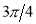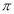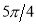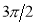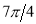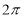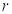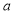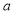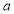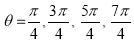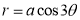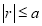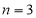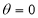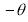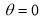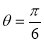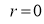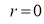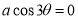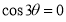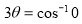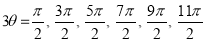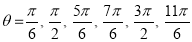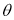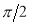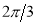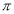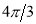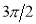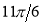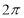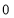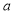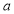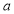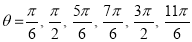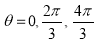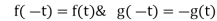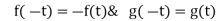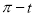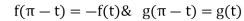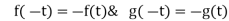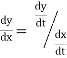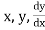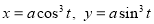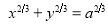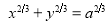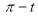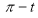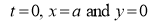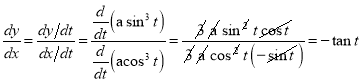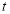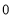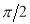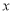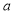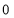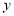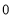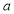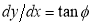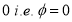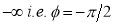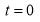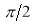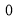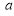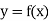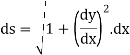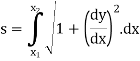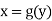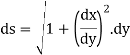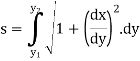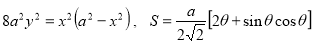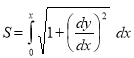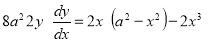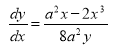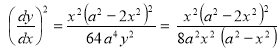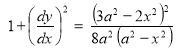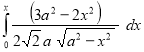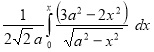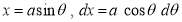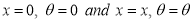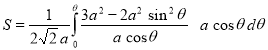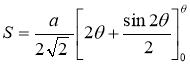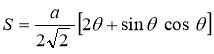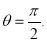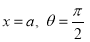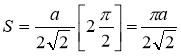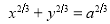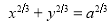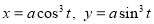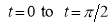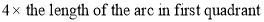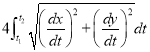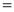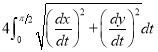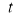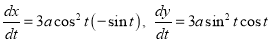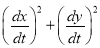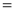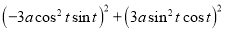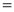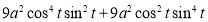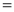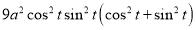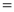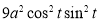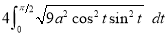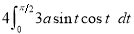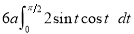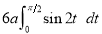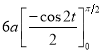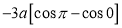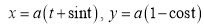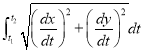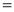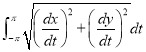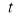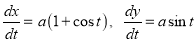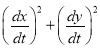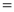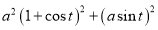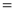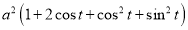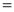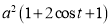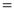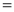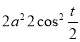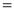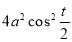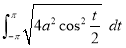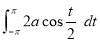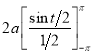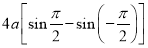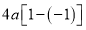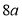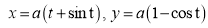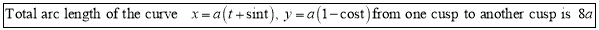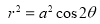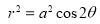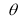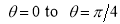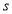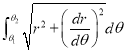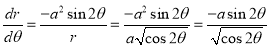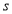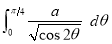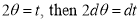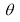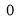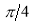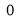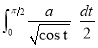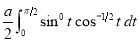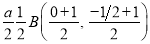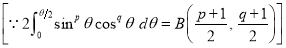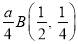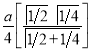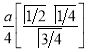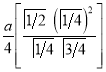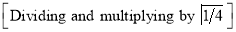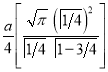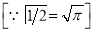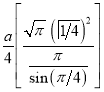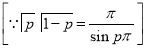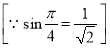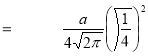Unit-4
CURVE TRACING
BASIC DEFINITIONS
- Convex Upwards: If the portion of the curve on both sides of point ‘A’ lies below the tangent at A, then the curve is convex upwards.
- Convex Downwards:If the portion of the curve on both sides of point ‘A’ lies above the tangent at A, then the curve is convex downwards.
- Singular points:An unusual point on a curve is called a singular point such as a point of inflexion, a double point, a multiple point, cusp, node or a conjugate point.
- Point of Inflexion: The point that separate the convex part of a continuous curve from the concave part is called the point of inflexion of the curve. i.e. A point where the curve unusually crosses its tangent is called a point of inflexion.
- Multiple Point:A point through which more than one branches of a curve pass is called a multiple point of the curve.
- Double point: A point on a curve is called a double point, if two branches of the curve pass through it.If r branches pass through a point, the point is called a multiple point of rth order.
- Node: A double point is called node if the branches of curve passing through it are real and the tangents at the common point of intersection are distinct.
- Cusp: A double point is called Cusp if the tangents at that point to the two branches of the curve are coincident.
- A Conjugate Point: A Point P is called a conjugate point on the curve if there are no real points on the curve in the vicinity of the point P. It is also called as an isolated Point.
Tracing of Cartesian curves The following rules will help in tracing a Cartesian curve. Rule 1: Symmetry (a) Symmetry about X-axis: If the equation of curve containing all even power terms in ‘y’ then the curve is symmetric about X-axis. (b) Symmetry about Y-axis: If the equation of curve containing all even power terms in ‘x’ then the curve is symmetric about Y-axis (c) Symmetry about both X and Y axes: If the equation of curve containing all even power terms in ‘x’ and ‘y’ then the curve is symmetric about both axes. (d) Symmetry in opposite quadrants: If the equation of curve remains unchanged when x and y are replaced by –x and –y respectively then the curve is symmetric in opposite quadrants. (e) Symmetry about the line (f) Symmetry about the line Rule 2: Points of intersection (a) Origin: If the equation of curve does not contain any absolute constant then the curve passes through the origin. (b) Intersection with the co-ordinate axes: Intersection with X-axis: put y=0 in the given equation and find the value of x. Intersection with Y-axis: put x = 0 in the given equation and find the value of y. (c) Points on the line of symmetry: If y=x is the line of symmetry then put y=x to find the points on line of symmetry. Rule 3:Tangents (a) Origin:If the curve passes through origin then the equations of the tangent at origin can be obtained by equating the lowest degree terms taken together to zero. (b) Other points: Tofind nature of tangent at any point find Case 1: If Case 2: If Case 3: If Case 4: If Rule 4:Asymptotes: (a) Parallel to X-axis: Asymptotes parallel to X-axis are obtained by equating the coefficient of highest degree term in x to zero. (b) Parallel to Y-axis: Asymptotes parallel to Y-axis are obtained by equating the coefficient of highest degree term in y to zero. (c) Oblique asymptote: Asymptotes which are not parallel to co-ordinate axes are called as Oblique asymptotes. Method 1: Let y=mx+c be the asymptote. The point of intersection with the curve f(x, y)=0 are given by f(x, mx+c)=0. Equate to zero the coefficients of two successive highest power of ‘x’, giving equations to determine m & c. Method 2:
Rule 5:Special points on the curve:Find out such points on the curve whose presence can be easily detected. Rule 6:Region of absence of the curve: Findthe values of x(or y) where y(or x) becomes imaginary, then the curve does not exists in that region. | |||||||||||||||||||||||||||||||||||||||||||
Q1) Trace the following curve: Sol)
| |||||||||||||||||||||||||||||||||||||||||||
Q2) Trace the following curve:
Sol)
| |||||||||||||||||||||||||||||||||||||||||||
|
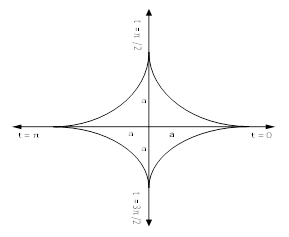
The following rules will help in tracing a Parametric curve Rule 1:Limitations of the curve: If possible, find the greatest and least values of x & y for a proper value of t. Rule 2: Symmetry: (a) Symmetry about X-axis: If ‘x’ is even and ‘y’ is odd w. r. t ‘t’ i.e. (b) Symmetry about Y-axis: 1. If ‘x’ is odd and ‘y’ is even w. r. t ‘t’ i.e. 2. For trigonometric functions if ‘x’ is odd and ‘y’ is even w. r. t ‘ i.e. axis. Symmetry in opposite quadrants: If ‘x’ and ‘y’ both are odd w. r. t ‘t’ i.e. quadrants. Rule 3: Points of intersections: It will pass through the origin if on putting t = 0 we obtain x = 0 and y = 0 . Also find the points of intersection of the curve and the axes. Rule 4: Nature of tangents: 1) 2) Form the table of values of Rule 5: Asymptotes and region: 1) Find asymptotes if any. 2) Find region of absence. | ||||||||||||||||||||||||||||||||||||
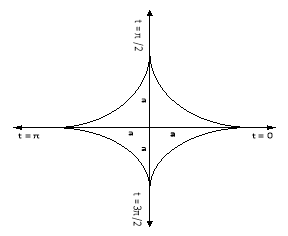
Q1) Trace the following curve:
Sol)
|
RECTIFICATION OF CURVES (Parametric and Polar Form) |
In this session we shall consider the application of integration to measure the length of an arc of Cartesian curve.
In this session we shall consider the application of integration to measure the length of an arc of parametric and polar curves. |
Ex1) Find the total arc length of the curve Sol)
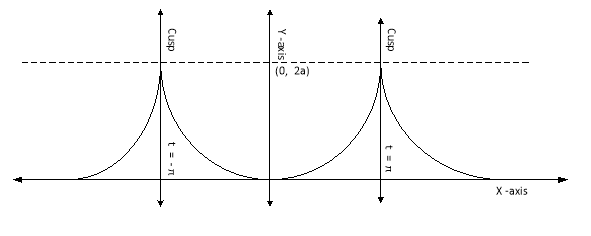
Ex2) Find the arc length of the cycloid Sol)
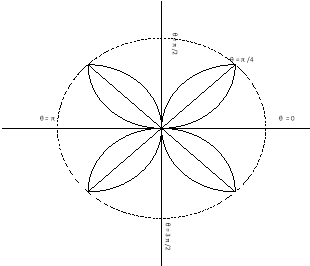
Ex3) Solve the following problems on Rectifications. (i) Find the length of upper arc of one loop of the curve Sol)
|
References:
- Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I and II) by P.N. Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune.
6. Differential Equations by S. L. Ross (John Wiley and Sons)