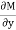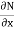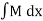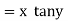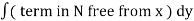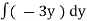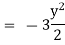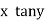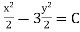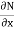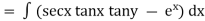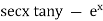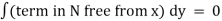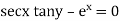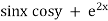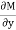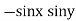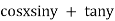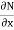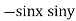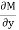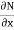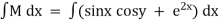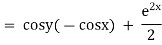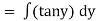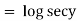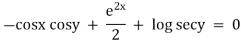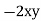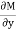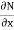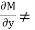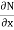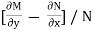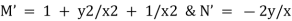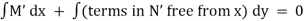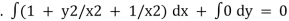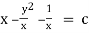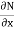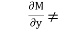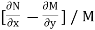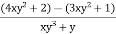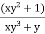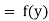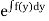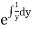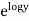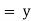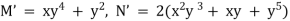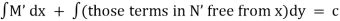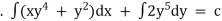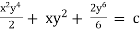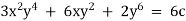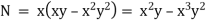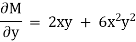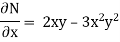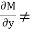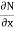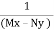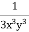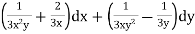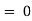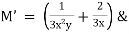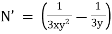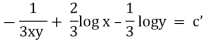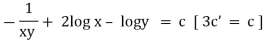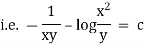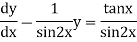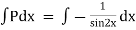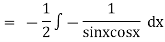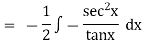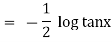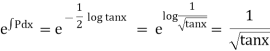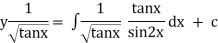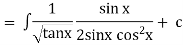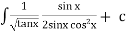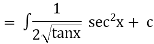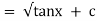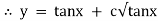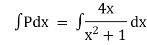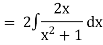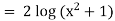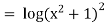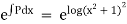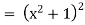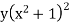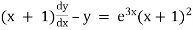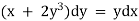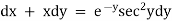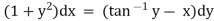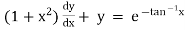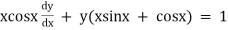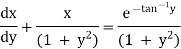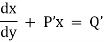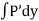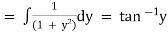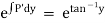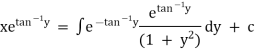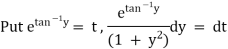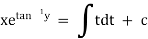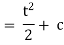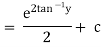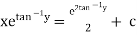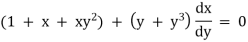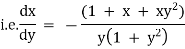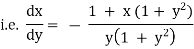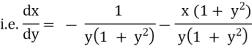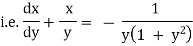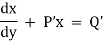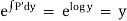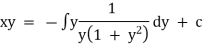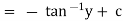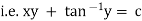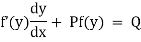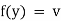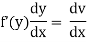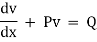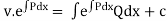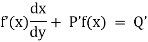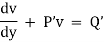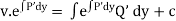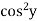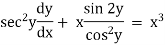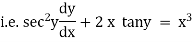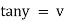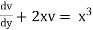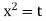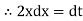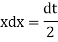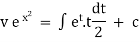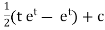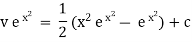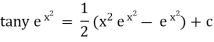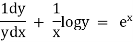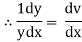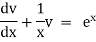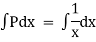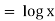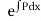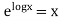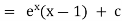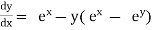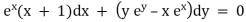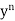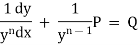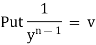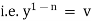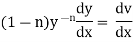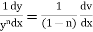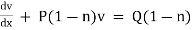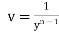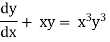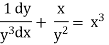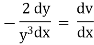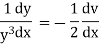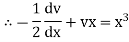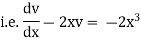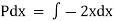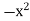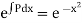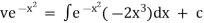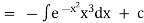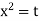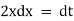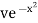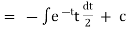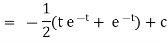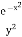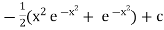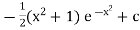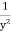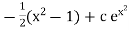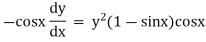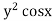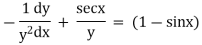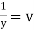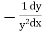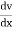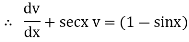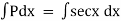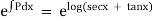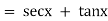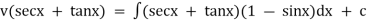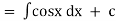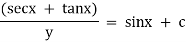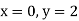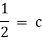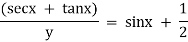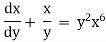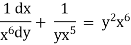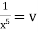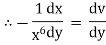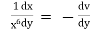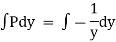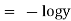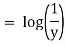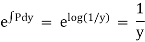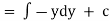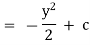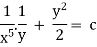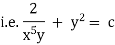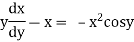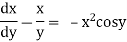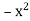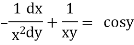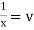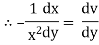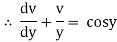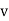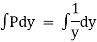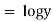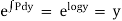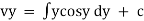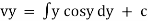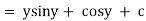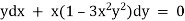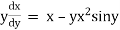Unit – 1
First Order Ordinary Differential Equation
Introduction :-
We know that how to form a differential equation from a given primitive. Now in this chapter we find the primitive from a given differential equation.
The process of obtaining such a primitive from a given differential equation is called solving the differential equation.
Differential Equation :-
An equation involving derivatives or differential coefficient is called differential equation.
Moreover if these derivatives are ordinary, then it is called ordinary differential equation and if they are partial then corresponding equation is called partial differential equation.
Order of the differential Equation :-
The order of differential equation is the order of highest order derivative occurring in that equation.
Eg. i). 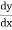 + cosx = 0
+ cosx = 0
is of order 1
ii). 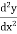 –
– 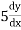 + 6y = 0 is of order 2.
+ 6y = 0 is of order 2.
Degree of the differential Equation :-
The degree of the differential eqn is the power / degree / index of the highest order derivative occurring in that equation.
Eg. (i). 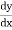 + sinx = 0
+ sinx = 0
Is of degree 1.
(ii). (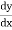 )2 – 5y = 0
)2 – 5y = 0
Is of degree 2.
First order First degree differential equationn :-
An equation of the form,
 or
or 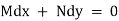
Where 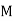 and
and 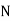 are functions in
are functions in 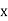 &
& 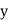 is called first order first degree differential Equation.
is called first order first degree differential Equation.
Solution of the differential Equation :-
Any relationship between dependent and independent variable, which satisfies the given differential equation is called solution of that differential Equation.
There are different methods for solving the differential equation of first order and first degree differential equation.
Viz.
(1). Exact differential Equation
[reducible to exact differential equation]
(2). Linear differential Equation
[ Reducible to Linear differential Equation ]
(3). Bernoulli’s differential Equation
Exact differential equation :-
A differential equation which is obtained from its primitive by differentiation only & without any operation of elimination or reduction is called exact differential equation.
Thus if u = c, where u is a function of 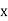 &
&  is a primitive then,
is a primitive then,
du = 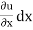 +
+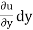
Rule for finding the solutions :
If 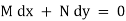 is an exact differential equation, it must have been obtained by equating to zero, total differential du of some function u of
is an exact differential equation, it must have been obtained by equating to zero, total differential du of some function u of 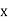 &
& 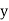 .
.
Since,
du = 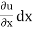 +
+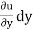
i.e. M = 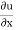 & N =
& N =  then
then
 we get a part of u & it’s partial derivative w. r .t
we get a part of u & it’s partial derivative w. r .t 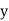 is in
is in 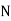 . the term in u which are free from x do not appear in M but they appear in N. Hence the remaining part of u is obtained by integrating w.r.t. y those terms in N. which are free from x. thus we get,
. the term in u which are free from x do not appear in M but they appear in N. Hence the remaining part of u is obtained by integrating w.r.t. y those terms in N. which are free from x. thus we get,
The Rule :-
Integrate 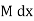 w.r.t. x treating y const, Integrate only those terms in N which are free from x w.r.t. y. equate the sum to a constant which is the required solution.
w.r.t. x treating y const, Integrate only those terms in N which are free from x w.r.t. y. equate the sum to a constant which is the required solution.
Ex : 1. Solve( tany + 3 ) dx + ( x sec2y – 3y ) dy = 0
Sol)
Here M = tany + x & N = xsec2y – 3y |
|
Now, |
|
|
& |
= |
|
The solution is |
|
Ex.2. solve(secx tanx tany - ex ) dx + secx sec2y dy = 0
Sol)
Here M = secx tanx tany |
|
& N = secx sec2y |
|
|
Given equation is an exact differential equation . |
Now |
|
= |
|
Thus |
|
which is the required solution |
Ex3) Solve(sinx cosy + e2x)dx + (cosx siny + tany) dy = 0
Sol)
Here M = |
|
& N = |
|
|
Given equation is an exact differential equation . |
Now |
|
|
& |
|
|
The solution is |
|
which is the required solution |
Equations Reducible to Exact differential Equation.
Sometimes the given differential equation is not exact but we can convert it into exact differential equation by multiplying it by a suitable factor, called integrating factor.
Then resultant equation can be solved by exact differential Equation method.
Rules for finding Integrating factor (I.F.)
Rule 1:-If 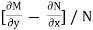 is a function in x only or constant say f(x) then
is a function in x only or constant say f(x) then 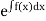 is an integrating factor.
is an integrating factor.
Ex1) Solve (x2 + y2 + 1)dx – 2xydy = 0
Sol)
Here M = x2 + y2 + 1, N = |
|
|
Given differential equation is not exact. |
Now consider, |
|
|
I.F. = |
= |
= |
= |
Multiplying IF to given diff equation we get an exact differential equation as, |
[ 1 + y2/x2 + 1/x2 ] dx – 2y/x dy = 0 |
Here |
Hence its solution is given by, |
|
i.e |
i.e. |
is the required solution of given differential equation. |
Exercise
Solve the following
(i). (x4ex – 2mxy2)dx + 2mx2y dy = 0
(ii). (2x2 - y)dx + (xy2 + 1)xdy = 0
(iii). (xsec2y – x2cosy)dy = (tany – 3x4)dx
Rule 2:- If  is a function of y only or constant say f(y) then
is a function of y only or constant say f(y) then 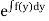 is an Integrating factor.
is an Integrating factor.
Ex) Solve(xy3 + y)dx + 2(x2y2 + x + y4)dy = 0
Sol)
Here M = xy3 + y, N = 2(x2y2 + x + y4) |
|
|
|
Given differential equation is not exact . |
|
Now consider, |
|
|
|
= |
|
IF = |
|
= |
|
= |
|
|
|
|
(xy4 + y2)dx + 2(x2y3 + xy + y5)dy = 0 |
|
Here |
|
Hence it’s solution is given by, |
|
|
|
i.e |
|
i.e. |
|
|
|
Is the required solution. |
Exercise
(i). (x2 + y2 + x)dx + xydy = 0
(ii). xex(dx - dy) + exdx + yeydy = 0
(iii). ydx – xdy = 0
Rule 3 :- If the equation is of the form f(xy) y dx + g(xy)xdy = 0 and
Mx – Ny ≠ 0 then 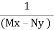 1is an integrating factor.
1is an integrating factor.
Rule 4 :- if the equation is of the form Mdx + Ndy = 0 where M and N are homogeneous expressions of same degree in x & y and Mx + Ny ≠ 0 then 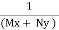 is an integrating factor.
is an integrating factor.
Ex) Solve y(xy + 2x2y2)dx + x(xy – x2y2)dy = 0
Sol)
Here |
|
|
|
|
Thus |
Given differential equation is not exact. |
Now consider, |
|
|
Then |
P.I = |
Now multiplying given equation by I.F. we get an exact differential Equation as |
|
Here, |
Hence its solution is given by, |
|
|
|
|
|
is the required solution of given differential equation. |
Exercise :-
Solve the following.
(i). y(1 + xy + x2y2)dx + x(1 – xy + x2y2)dy = 0
(ii). y(sinxy + xy cosxy)dx + x(xy cosxy - sinxy)dy = 0
(iii). (x2y – 2xy2)dx – (x3 – 3x2y)dy = 0
(iv). x2ydx – (x3 + y3)dy = 0
(v). y(x + y)dx – x(y - x)dy = 0
Linear Equations :-
A differential equation is said to be linear if the dependent variable and its derivatives appears only in the first degree. The form of the linear differential equation of the first order is

Where P & Q are functions of x or constant only.
A linear equation of the form 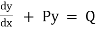 is not solvable as it is.
is not solvable as it is.
However if we multiply it by the factor 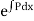 it becomes exact & hence can be solved by the usual method.
it becomes exact & hence can be solved by the usual method.
To solve the equation 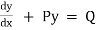 :-
:-
Multiply the given equation by the I.F. 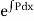 , we get,
, we get,
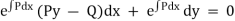
Since, it is exact, we have
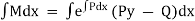

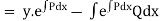
Since there is no term in N free from x, the solution is
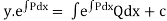
Remark :-To solve a linear differential equation, first write the equation with the coefficient of  unity.
unity.
i.e. in the form 
Then find 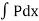 and further
and further 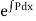
Then the solution is.
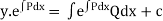
Ex) sin2x 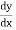 = y + tanx
= y + tanx
The given equation can be written as, |
|
which is a linear diff. eqn. |
Now |
|
|
|
|
Thus the solution is. |
|
|
= |
|
|
|
Which is the required solution. |
Ex) 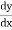 +
+ 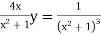
Sol)
This is a linear differential equation |
Considr |
|
|
|
|
|
|
Hence it’s solution is, |
|
|
|
Exercise:
Another form of linear differential equation :-
A differential equation of the form

where 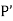 &
& 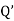 are functions of y only is also a linear differential eqn with x & y having interchanged positions & Hence it’s solution is
are functions of y only is also a linear differential eqn with x & y having interchanged positions & Hence it’s solution is

Ex) 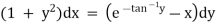
Sol)
The given eqn can be written as, |
|
which is a linear diff eqn of the form |
|
Now |
|
Hence it’s solution is |
|
|
|
|
|
|
Thus |
|
Is the required solution of given du=ifferential equation. |
Ex) (1 + x + xy2)dy + (y + y3)dx = 0
Sol)
The given eqn can be written as, |
|
|
|
|
|
which is of the form, |
|
Now, |
|
|
Hence solution is, |
|
|
|
Equation reducible to the linear form. |
An equation of the type |
|
where P and Q are functions of x only can be reduced to the lined form as, |
put |
|
given eqn becomes |
|
which is a linear & it’s solution is |
|
Simillarly an equation of the form. |
|
can be reduced to |
|
& it’s soln is |
|
Ex) 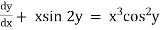
Sol)
Dividing by |
|
|
|
Put |
|
|
|
|
Hence it’s solution is |
|
Put |
|
|
|
= |
Thus |
|
i.e. |
Ex) 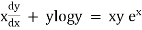
Sol)
Dividing by |
|
Put |
|
Thus we get, |
|
which is a linear equation |
Now consider |
|
|
Thus |
I.F.= |
Hence it’s solution is given by , |
|
|
|
Thus |
Is the required solution. |
Exercise
An equation of the form
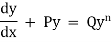
where P and Q are functions of x alone, is called Bernoulli’s equation & it is reducible to linear form by dividing it by 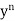 and then putting
and then putting 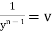 v. after simplification it can be solved by previous method.
v. after simplification it can be solved by previous method.
Method to solve |
Dividing by |
|
|
|
|
|
i.e. |
thus we get, |
|
i.e. |
which is a linear in x. after solving it we substitute |
Ex) 
Sol)
The given eqn can be written as |
|
This is a Bernoullis eqn. |
Dividing by |
|
Put |
|
|
|
|
which is a linear equation in v |
Now ∫ |
Thus I.F.= |
Thus it’s solution is, |
|
|
Put |
|
|
Thus |
|
|
Thus |
|
Which is the required solution. |
Ex) 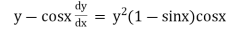
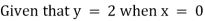
Sol)
We have, |
|
Dividing by |
|
Put |
|
|
which is a linear equation in v. |
Now |
|
|
|
Hence It’s soln is, |
|
|
|
|
|
Thus |
|
which is the required soln. |
Now when |
|
|
is the required solution. |
Exercise :
Solve 
Solve 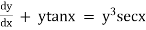
Solve 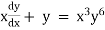
Another form of Bernoulli’s equation:-
A differential equation of the form 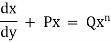
is also of Bernoulli’s form with x & y having change their positions. By dividing by 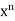 and putting
and putting 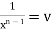 we can reduce it to a linear form.
we can reduce it to a linear form.
Ex) 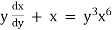
Sol)
The given eqn can be written as, |
|
Dividing it by |
|
Put |
|
i.e. |
|
which is a linear equation in v |
Now |
|
|
|
|
Hence It’s solution is, |
|
|
|
Thus |
|
|
which is the required solution. |
Ex) 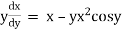
Sol)
The given eqn can be written as, |
|
|
dividing it by |
|
|
Put |
|
|
which is a linear in |
|
|
|
Thus soln is, |
|
|
|
|
Thus |
|
is the required solution. |
Exercise :
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I and II) by P.N. Wartikar and J.N.Wartikar Vidyarthi
Griha Prakashan, Pune.
6. Differential Equations by S. L. Ross (John Wiley and Sons)