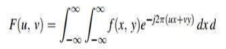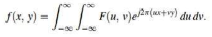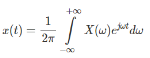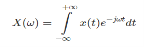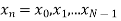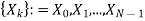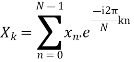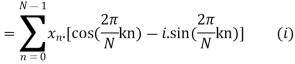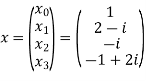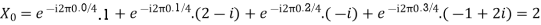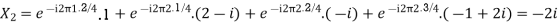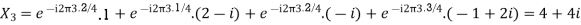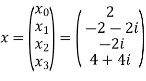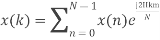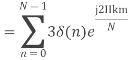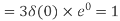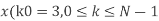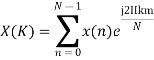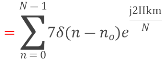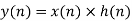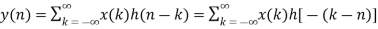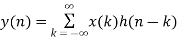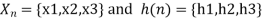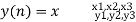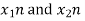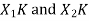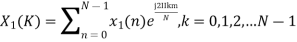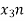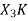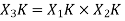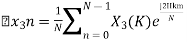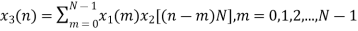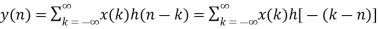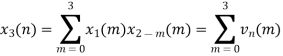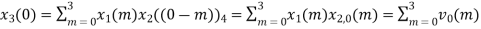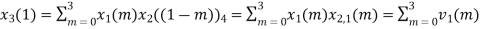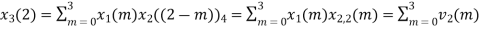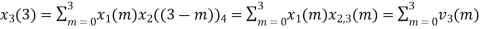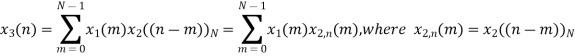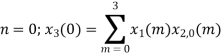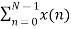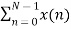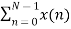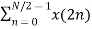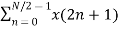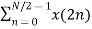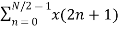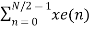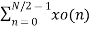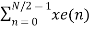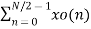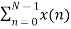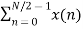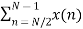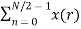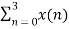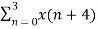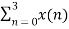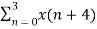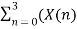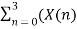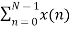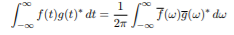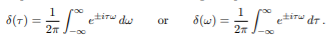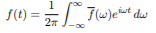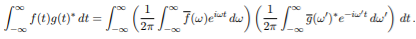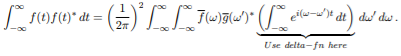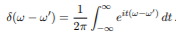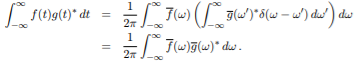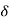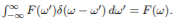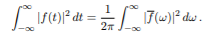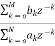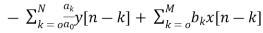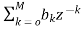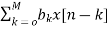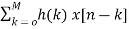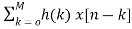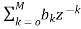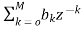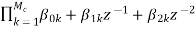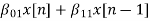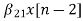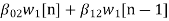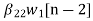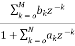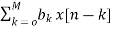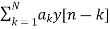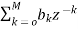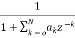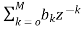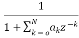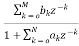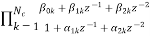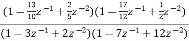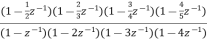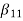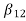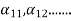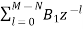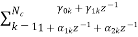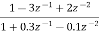Unit-3
Discrete Fourier Transform
We first transform the image to its frequency distribution. Then our black box system performs whatever processing it has to performed, and the output of the black box in this case is not an image, but a transformation. After performing inverse transformation, it is converted into an image which is then viewed in spatial domain. A signal can be converted from time domain into frequency domain using mathematical operators called transforms. There are many kinds of transformation that does this. Some of them are given below.
Fourier series simply states that, periodic signals can be represented into sum of sines and cosines when multiplied with a certain weight.It further states that periodic signals can be broken down into further signals with the following properties.
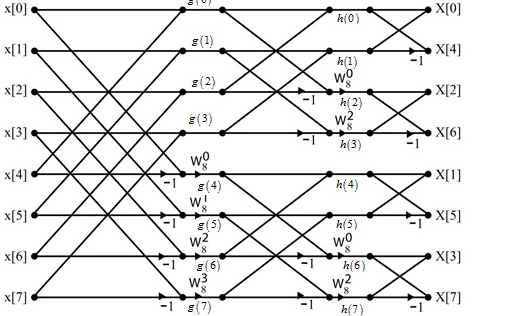
The Fourier Series is given by
The inverse is given by
The Fourier transform simply states that that the non-periodic signals whose area under the curve is finite can also be represented into integrals of the sines and cosines after being multiplied by a certain weight. The Fourier transform is given by
The inverse is given as
The Fourier transform has many wide applications that include, image compression (e.g JPEG compression), filtering and image analysis.
Key takeaway The Fourier transform is given by
|
The discrete Fourier transform transforms a sequence of N complex numbers
Example: Let N =4 and
Here we demonstrate how to calculate the DFT of x using equation (1)
|
Linear Property If x(t) -> X(w) Y(t) -> Y(w) then a x(t) + b y(t) -> a X(w) +b Y(w)
If x(t)⟷F.TX(ω) Then Time shifting property states that x(t−t0)⟷F.T e−jω0t X(ω)
If x(t)⟷X(ω) Then frequency shifting property states that ejω0t.x(t)⟷X(ω−ω0)
If x(t)⟷X(ω) Then Time reversal property states that x(−t)⟷X(−ω)
If x(t)⟷X(ω) Then Differentiation property states that dx(t)dt⟷jω.X(ω) dnx(t)dtn⟷(jω)n.X(ω)
Integration Property Integration property states that ∫x(t)dt⟷1jω X(ω)
Then
∭...∫x(t)dt⟷(jω)n X(ω)
Multiplication and Convolution Properties If x(t)⟷X(ω) y(t)⟷Y(ω) Then multiplication property states that x(t).y(t)⟷X(ω)∗Y(ω) and convolution property states that x(t)∗y(t)⟷1/2πX(ω).Y(ω)
Key takeaway
Examples
Compute the N-point DFT of x(n)=3δ(n).
Compute the N-point DFT of x(n)=7(n−n0) Solution − We know that,
Substituting the value of x(n),
|
Linear Convolution states that y(n) = x(n) * h(n)
Example 1: h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n). METHOD 1: GRAPHICAL REPRESENTATION Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n)) Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1
METHOD 2: MATHEMATICAL FORMULA Use Convolution formula
k= 0 to 3 (start index to end index of x(n)) y(n) = x(0) h(n) + x(1) h(n-1) + x(2) h(n-2) + x(3) h(n-3)
METHOD 3: VECTOR FORM (TABULATION METHOD) X(n)= {x1,x2,x3} & h(n) ={ h1,h2,h3}
y(-1) = h1 x1 y(0) = h2 x1 + h1 x2 y(1) = h1 x3 + h2x2 + h3 x1 …………
METHOD 4: SIMPLE MULTIPLICATION FORM
Circular convolution
Let us take two finite duration sequences
Now we will try to find the DFT of another sequence
By taking the IDFT of the above we get
After solving the above equation finally we get
Methods of Circular Convolution Generally, there are two methods, which are adopted to perform circular convolution and they are −
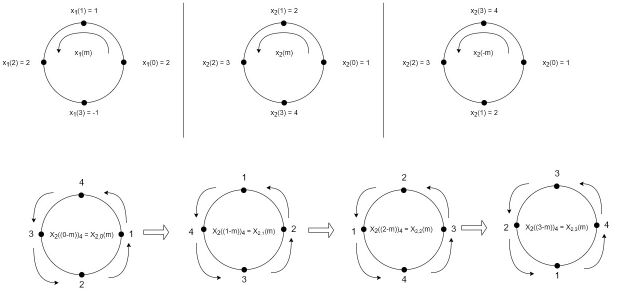
Let x1(n) and x2(n) be two given sequences. The steps followed for circular convolution of x1(n) and x2(n) are
Matrix method represents the two given sequence x1(n) and x2(n) in matrix form.
Key takeaway y(n) = x(n) * h(n)
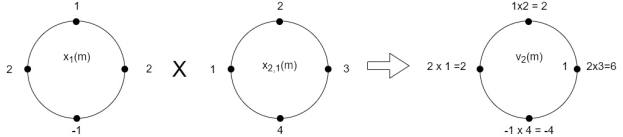
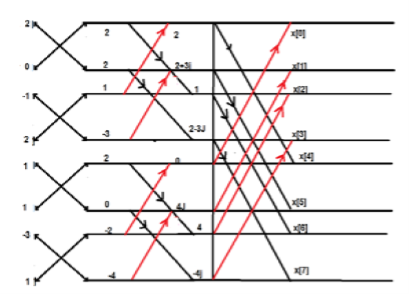
Examples Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4} Sol:
Fig 1 Circular Convolution of x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}
(2)
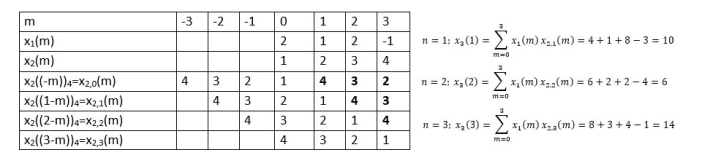
When n=0;
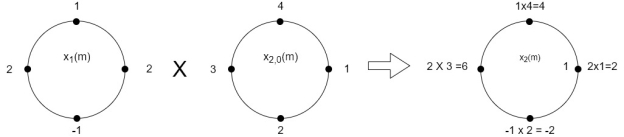
The sum of samples of v0(m) gives x3(0) ⸫ x3(0)=2+4+6-2=10 When n=1;
The sum of samples of v1(m) gives x2(1) ⸫ x3(1)=4 + 1 +8-3=10
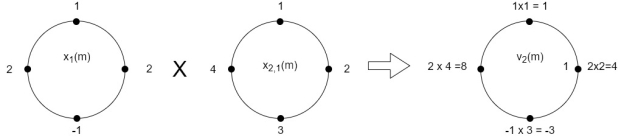
(3)When n=2;
The sum of samples of v2(m) gives x3(2) ⸫ x3(2)=6+2+2-4=6
(4) When n=3;
The sum of samples of v3(m) gives x3(3) ⸫ x3(3)=8+ 3+ 4-1= 14 x3(n)={10,10,6,14}
= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3) = 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10 |
Certain algorithms permit implementations of Discrete Fourier transform with considerable savings in computation time. These algorithms are known as Fast Fourier Transform.
FFT algorithm are based on fundamental principle of decomposing the computation of DFT of sequence length into successively smaller discrete Fourier transforms.
They are basically two classes of FFT algorithms
Decimation-in-time algorithm
This algorithm is known as Radix-2 DIT-FFT algorithm which means the number of output points N can be expressed as a power of 2 that is N = 2M where M is an integer.
Let x(n) be a sequence where N is assumed to be a power of 2. Decimate or break this sequence into two sequences of length N/2 where one sequence consists of even-indexed values of x(n) and the other of odd-indexed values of x(n). xe(n) = x(2n) n= 0,1,……….. N/2-1 xo(n) = x(2n+1) n= 0,1,……….. N/2 -1 The N-pt DFT of x(n) can be written as X(k) = Separating x(n) into even and odd indexed values of x(n) we obtain X(k) = ( n even) (n odd)
= = X(k) = WN2 =( e-j2π/N) 2 = e-j2π/N/2 = W N/2 . WN2 = W N/2 X(k) =
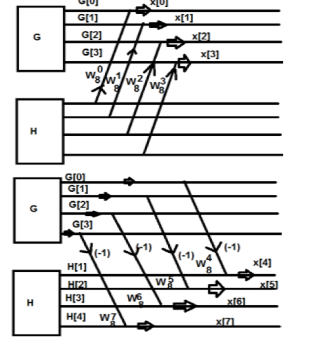
Fig 2 Decimation in time algorithm
W84 = -1 W8 5 = - W 81 W86 = - W82 W87 = - W83 G(0) – H(0) = x(4) G(1) - W 81 H(1) = x(5) G(2) - W82 H(2) = x(6) G(3) - W83 H(3) = x(7)
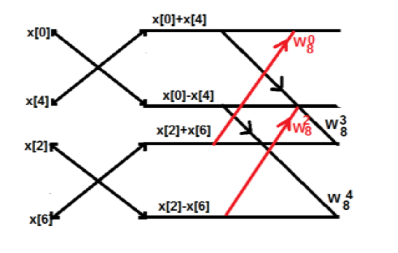
Fig 3 Butterfly Diagram to find W08-W38 Consider the sequence x[n]={ 2,1,-1,-3,0,1,2,1}. Calculate the FFT. Arrange the sequence as x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7) Since N=8 find the values W8 0 to W 87 Apply the butterfly diagram to obtain the values.
Fig 4 Butterfly Diagram
Decimation in Frequency FFT Apart from time sequence, an N-point sequence can also be represented in frequency. Let us take a four-point sequence to understand it better.
Let the sequence be x[0],x[1],x[2],x[3]………..x[7]
Mathematically, this sequence can be written as; X(k) = Now let us make one group of sequence number 0 to 3 and another group of sequence 4 to 7. Now, mathematically this can be shown as = Let us replace n by r, where r = 0, 1 , 2….N/2−1. = We take the first four points x[0],x[1],x[2],x[3] initially, and try to represent them mathematically as follows –
= = X[0] = X[1] =
= X(0) – X(4) + (x[1] – X[5]) W8 1 + ( X[2] – X[6] )W82 + X(3) – X(7) W8 3
Fig 5 DIF –FFT Algorithm
Find the DIF –FFT of the sequence x(n)= { 1,-1,-1,1,1,1,-1} using Dif-FFT algorithm.
X(0)= 20 X(4) =0 X(1) = -5.828- j2.414 X(5) = -0.1716 + j 0.4141 X(2) = 0 X(6) = 0 X(3) = -0.171 – j 0.4142 X(7) = -5.8284 + j2.4142
Key takeaway The N-pt DFT of x(n) can be written as X(k) =
|
The below give equation is called as Plancherel’s formula
The integral of delta function is given as shown below
The inverse Fourier transform is shown as
From 1 can write
Rearranging the above equation we have
The integral representation of
The equation 7 is obtained because of the
The Parseval’s Theorem is given below
|
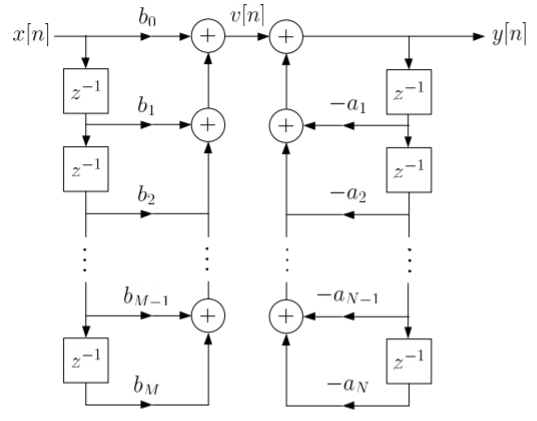
The basic realization techniques used for filters are direct form, cascade form and parallel form. In this section we will study all in detail. This section overviews ability to implement finite impulse response (FIR) and infinite impulse response (IIR) filters using different structures in terms of block diagram and signal flow graph. For an LTI system the transfer function is given as H(z)= The difference equation can be written as
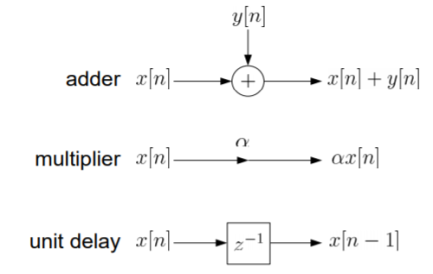
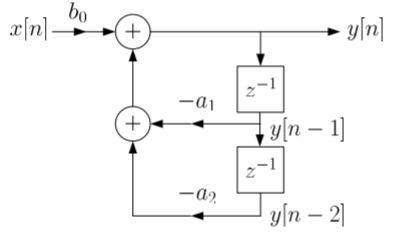
x(n)= system input y(n)=system output when a0≠ The above equation implementation requires some basic blocks shown below Fig 6 Block diagram representation The above blocks can be easily understood with the help of one example. For the standard LTI system with difference equation Y[n]=-a1y[n-1]-a2y[n-2]+b0x[n]. Draw the block diagram for the given equation.
Sol: We already know that x[n] and y[n] are the input and output to the system respectively.
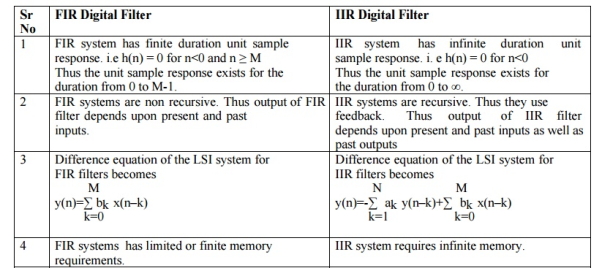
Fig 7: Block diagram representation FIR FILTER: The standard equation for representing the FIR filter is shown below H(z)= From equation (1) and (4) we can conclude that FIR filters do not contain any pole. The difference equation will be Y[n]= a) Direct Form: The direct form is directly derived from the difference equation. It can be represented as y[n]= where h(k) is the system impulse response. Expanding the above equation, we get Y[n]= The block diagram representation for above direct form is shown below.
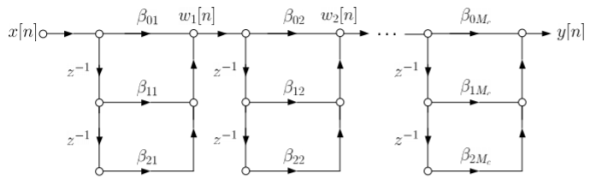
Fig 8: Direct form realization of Fir filter b) Cascade Form: As we already know H(z)= The above equation can be represented as a product of second order polynomial as H(z)= Mc=|(M+1)/2| The above equation can be further simplified with intermediate output of system 1 w1(n) fed to the input of second cascade structure and so on. The difference equation is given as w1(n)= w2(n)=
Fig 9: Cascade form FIR filter
IIR FILTER: The transfer function of IIR filter is given as H(z)= From above equation we can conclude that an IIR filter contains at least one pole. a) Direct Form: The direct form is realised directly from its difference equation v[n]=
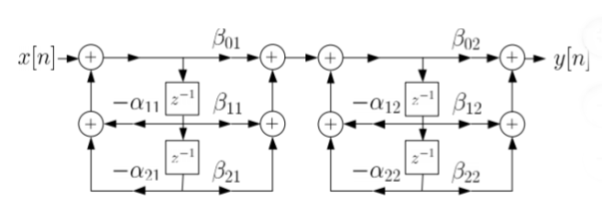
y[n]=- Another way to obtain direct form is by decomposing H(z) into two transfer functions H(z)=H1(Z). H2(z) H1(Z)= H2(z)= V(z)=X(z). H1(Z)=X(z) Y(z)=V(z). H2(z)=V(z) The final realisation block diagram representation of direct form for IIR filter is shown below Fig 10: Direct Form realization of IIR Filter b) Cascade form: To find the transfer function for cascade for we need to factorize the numerator and denominator polynomials in terms of second order polynomial. H(z)= Nc=|(N+1)/2| Let us consider M=N=4. Then the cascade realisation for IIR filter is shown below.
Fig 11: Cascade Form realisation of IIR Filter
Que) For the following LTI system H(z)=
Sol: H(z)= The above function can be simplified as H(z)= Hence, using the above structure and placing the values of
c) Parallel form: The parallel form is given as H(z)= Nc=(N=2)/2
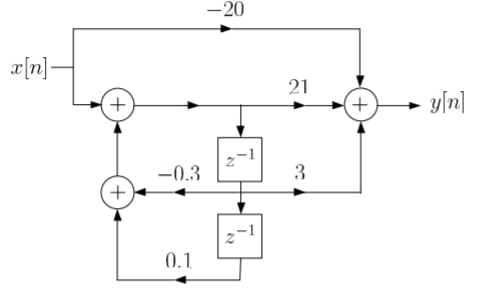
Que) Draw block diagram for the function using parallel form H(z)= Sol: H(z)= Writing above transfer function in standard form for parallel realisation we get H(z)=-20+ The structure is shown below
Key takeaway
|
References:
1. S. K. Mitra, “Digital Signal Processing: A computer based approach”, McGraw Hill, 2011.
2. A.V. Oppenheim and R. W. Schafer, “Discrete Time Signal Processing”, Prentice Hall, 1989.
3. J. G. Proakis and D.G. Manolakis, “Digital Signal Processing: Principles, Algorithms And Applications”, Prentice Hall, 1997.
4. L. R. Rabiner and B. Gold, “Theory and Application of Digital Signal Processing”, Prentice Hall, 1992.
5. J. R. Johnson, “Introduction to Digital Signal Processing”, Prentice Hall, 1992.
6. D. J. DeFatta, J. G. Lucas andW. S. Hodgkiss, “Digital Signal Processing”, John Wiley & Sons,1988.