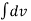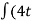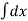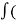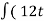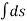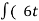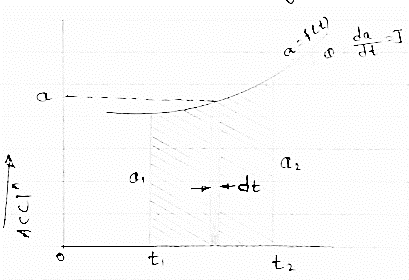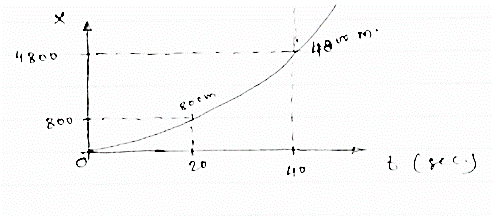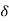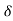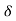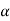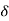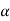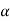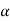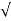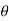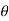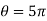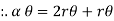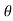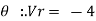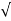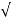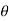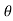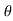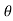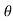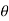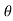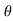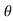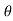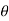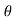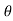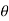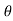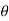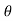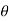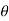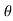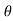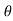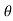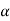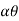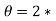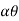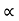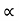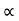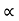UNIT 5
Kinematics of Particle
Motion:
A body is said to be motion it is changing its position w. r.t. reference point.
Speed:
Role of change of distance w.r.t. time but irrespective of the direction. It is scalar quantity. It is always positive.
Velocity: (V=x/t)
Rate of change of displacement w.r.t. time in a particular direction. It is vector quantity.
Displacement: (change in position of particle)
Shortest distance between initial and final position of a particle during motion. It may positive or negative. It is denoted by ‘s’ or ‘x’.
Distance:
Total path covered by α particle during given time interval. It is always positive. It is denoted by ‘s’ or ‘d’.
Distance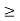 Displacement
Displacement
Average speed and instantaneous speed:
The avg. speed of particle is the distance travelled in the particular time interval.
If particle travels the distance ‘s’ in the time t1 to t2 then avg. speed,
Vavg = 
Instantaneous speed is the speed of particle at a particular instant when time interval approaches to zero. Then instantaneous speed,
V = 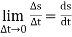
Average velocity and instantaneous velocity: -
Avg. velocity is the ratio of displacement as (or ∆x) to the time interval ∆t
Avg. velocity =∆x/∆t
Instantaneous velocity is the role of change of displacement when time interval Approaches to zero.
Instantaneous velocity=
V=dx/dt
Velocity may be positive or negative.
Avg. acceleration and instantaneous acceleration: -
Avg. acceleration is the rate of change of velocity of a particle for the time interval ∆t.
A (avg.) = ∆v/∆t
Instantaneous acceleration is the rate of change of velocity of a particle at particular instant when time interval ∆t approaches to zero.
Instantaneous acceleration = A = = dv/dt
= dv/dt
But v = dx/dt ; A = d/dt (dx/dt)
; A = x/
x/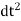
By chain rule ,
A = dv/ ds x ds/dt
A = dv/ds x v
; A = v. dv/ds
It may be positive or negative
Rectilinear Motion
Linear (Rectilinear) motion: -
The motion of the particle along the straight line is called as Rectilinear motion.
Uni-directional → Particle moving only in one direction.
Uni-directional → Forward & reverse motion of particle.
Uniform motion (u.m.)
[motion with zero acceleration]: -
If the particle is moving with constant velocity and zero acceleration.
The motion the particle is called as uniform motion.
Thus, here,
V=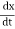 = constant.
= constant.
Taking integration,
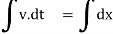
V 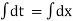
 V
V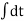
X = V × t
X = velocity x time
Examples on Uniform Motion – Velocity constant
(acceleration is zero)
1)In a race of 100 m distance, a runner runs at constant velocity from 30 m to 100 m position at velocity 12 m/s. Find the time required for the runner to cover the distance from 30 m position to 70 m position.
→V = 12 m/s
X1= S1 = 30m
X2= S2 = 70m
Distance covered / displacement = find position - initial position.
X =S = S2 - S1 = X2 – X1
= 70 - 30
X = S =40 m
For uniform motion
Displacement / Distance = V x T
40 = 12 x t
T = 40 / 12
T = 3.3.33 sec.
2) a train accelerates uniformly & gains the speed of 90 kmph. & runs at this speed for 17 minutes before getting slowed down due to work in progress .Find the distance covered by the train while running at the constant speed.
→
V =90 kmph = 90 x 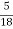 = 25 m/sec.
= 25 m/sec.
T = 17 minutes = 17 x 60 =1020 sec.
Distance covered / displacement
Of train while running = v x t
At constant speed
S = x = v x t
S = x = 25 x 1020
= 25500 m.
S = x = 25.5 km
Train covers 25.5 kms before getting slowed down due to work in progress.
sRectilinear motion with uniform (constant) acceleration :- [ U.A.M. - uniform acceleration motion]
|
→ Consider linear motion of particle starting from a & moving along ox with uniform acceleration .
→ let P is the position of particle after T sec.
→ Let u = initial velocity
V = final velocity
T = time taken by particle to change its velocity from u to v.
A = uniform positive acceleration
X or S = Displacement in ‘ t ‘ seconds .
Since , in ‘t’ seconds velocity of particle has increased steadily from ( u ) to ( v )
At the rate of acceleration ‘a’ ,
Total increase in velocity
= at
Final velocity , V = u + at - (1)
Average velocity = (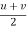 )
)
As we know that , Displacement by the particle ,
S = avg. velocity x time
S = (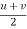 ) t → (11)
) t → (11)
Substituting value of v from equation (1)
S = (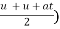 t
t
= (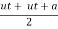 t2)
t2)
= (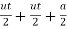 t2)
t2)
= (ut + t2)
t2)
S =ut +  at2 - eqn.. (11)
at2 - eqn.. (11)
From eqn.. (1) , V = u + at
T =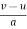 - put this value in (11)
- put this value in (11)
S = ( )
)
= v2 – u2 / 2a
2as = v2 - u2
V2 = U2 + 2as - (iv)
Thus the equations of motion are
1) V = u + at
2) S = ut +  at2
at2
V2= u2 + 2a
Examples on – motion with uniform acceleration
UAM – uniform acceleration motion.
(acceleration is constant )
1) a car starting from rest is accelerated at the rate of 0.4 m/s2 , find the distance covered by the car in 20 seconds.
→
GIVEN :- initial velocity = u= 0 ---------------- car is starting from rest.
Acceleration = a = 0.4 m/s2
Time = t = 20 sec.
We know that the equation of motion for displacement.
S =ut +  at2
at2
= (0 x 20 ) +  x 0.4 x202
x 0.4 x202
S = 80m.
Car will cover 80 m distance in 20 seconds .
2) a train travelling at 27 kmph is accelerated at the rate of 0.5 m/sec2 . what is the distance travelled by train in 12 seconds .
→
GIVEN :- initial velocity = u = 27 kmph = 27 x 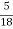 = 7.5 m/sec.
= 7.5 m/sec.
Acceleration = a = 0.5 m/sec2
Time = t = 12 sec.
From eqn of motion ,
S =ut +  at2
at2
= (7.5 x 12 ) + (  x 0.5 x 122)
x 0.5 x 122)
S = 90 + 36
‘ S = 126 m.’ ---------------------- distance travelled by train
A car comes to complete halt from an initial speed of 50 kmph in distance of 100 m. with same constant retardation what would be stopping distance from an initia speed of 70 kmph ?
→
GIVEN:- U1 = 50 kmph = 13.89 m/sec.
S1 = 100 m
V1 = 0
When initial speed is 50 kmph ,
We know that , V12= U12 + 2 as1
0 = 13.892 + 2a x 100
0 = 192.9 + 200 a
A =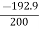
A = -0.964 m/s2 (-ve sign indicates retardation)
When initial speed is 70 kmph
i.e. u = 70 kmph = 70 x 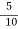 = 19.44 m/sec
= 19.44 m/sec
then ,
V22= U22 +2 as2
0 = 19.442 + 2 x (-0.964) x S2
0 = 378.09 -1.928 S2
-1.928 S2 = -378.09
S2 = 
S2 = 196.10 m
If the initial speed of the car is 70 kmph , then it will stop after covering 196.1 m distance.
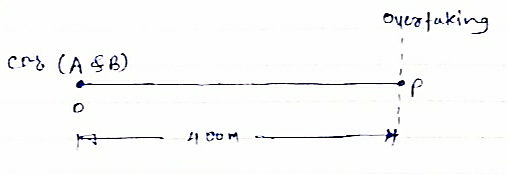
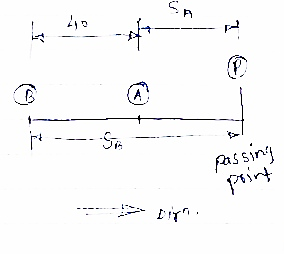
Two trucks A & b travelling in the same direction on same adjacent lanes are stopped at traffic signal. As the signal turns green , truck a accelerates at a constant rate of 20 m/sec2 . three seconds later , trucks B starts and accelerates at 3.6 m/s2 .find (1) when & where truck B will overtake (2) speed of each truck at the same time .
→
Truck A→ u = 0 m/s
a = 2 m/s2
Diagram
|
Truck B → u = 0 m/s
a= 2 m/s2
tb = time required = ( tA - 3) ( from signal to point p ).
(1) For truck a ,
Distance covered from signal to point ‘p’ = Sa
SA = utA +  atA2
atA2
= 0 +  x 3.6 ( tA - 3)2
x 3.6 ( tA - 3)2
SB = 1.8 (tA - 3)2--------------------------(11)
As the distance covered by both trucks from signal to point P is same ,
SA = SB
TA2 = 1.8 (tA – 3)2
TA2 = 1.8 ( tA2 - 6tA + 9 )
TA2- 1.8 tA2 + 10.8 TA - 16.2 = 0
-0.8tA2 + 10.8 tA - 16.2 = 0
Solving aboveeqn , tA= 1.718 sec &tA = 11.78 sec.
As tA = 1.718 < 3 sec , it can’t be considered .
TA = 11.78 sec
Truck B will overtake A at tA = 11.78 sec.
Distance covered by truck a during 11.78 sec ,
SA = tA2 = 11.782 = 138.76 m.
Truck B will overtake truck A after 138.76 m from signal.
3) speed of each truck. After t= 11.78 sec & at s = 138.76 m.
VA = u + at
VA =uA + aAtA
VA = 0 + 2 x 11.78
VA = 23.56 m/sec.
Similarly ,
VB = UB + aBtB
VB= 0+ 3.6 + ( tA – 3)
= 0 + 3.6 (11.78 - 3)
VB = 31.608 m/sec.
Ans:
Time required to overtake = 11.78 sec.
Distance covered before overtaking = 138.76 m
VA = 23.56 m/s
VB = 31.608 m/ sec. while overtaking
A train which is at rest starts from station with constant acceleration of 5 m/s2 , 3 seconds later another train passes the same station on the same line & in same direction with constant velocity . find the velocity of 2nd train to just avoid collision .
→
Let train A = a train starts from the station .
Train B a train passing the same station after 3 seconds .
(1) Consider train A - constant acceleration (UAM)
U = 0………..starts from rest
A = 5 m/s2
Let tA = time taken by train to cover SA distance .
S = utA +  atA2
atA2
S = (0 x tA ) + ( x 5 x tA2 )
x 5 x tA2 )
SA = 2.5 tA2 - (1)
2) consider Train B - constant velocity - (UM ) - :-
Let tB = time taken by train B to cover SB distance
TB = ( tA - 3 ) sec
For uniform motion ,
S = velocity x time
SB = vB x ( tA– 3) -------(2)
Now to just avoid the collision distance travelled by both trains must be same .
SA = SB
2.5 tA2 = VB ( tA - 3)
VB = 2.5 tA2/ (tA - 3 ) ---------------------- (3)
But ,
As velocity of train B is constant .
i.e. VB= constant ,
dvA /dt = aB = 0
thus,
dvA / dt = d / dt ( 2.5 tA2 / tA - 3 )
using quotient rule to take derivative.
dvA/ dt = aB = ( tA-3 ) ( 5tA) - ( 2.5 tA2) (1) / ( tA – 3 ) 2
0 = 5tA2 - 15 tA - 2.5 tA2 / ( tA – 3)2
0 = 5 tA2 - 15 tA - 2.5 tA2
2.5 tA2- 15 tA =0
2.5 tA2= 15tA
2.5 tA = 15
[ TA = 15 / 2.5 ]
{ TA = 6 sec. }
From equation (1)
S = 2.5 tA2
= 2.5 x 6 x 6
SA = 90 m
From equation (3)
VB = 2.5 tA2 / ( tA - 3)
=2.5 x 6 2 / (6 -3 )
[ VB = 30 m/sec ]
From equation (2 )
SB = VB (tA– 3 )
= 30 (6 -3 )
SB = 90m
Ans:-
Velocity of second train to just avoid collision should be
[ VB= 30 m/sec ]
A car A starts from rest and accelerates uniformly on the straight road. Another car B starts from the same point after 6 sec; with zero initial velocity & accelerates at 5m/sec2 uniformly. If car B overtakes car A at 400m from starting point; determine acceleration of car A & velocity of each car while overtaking
|
(1 ) for car A - (UAM ) from 0 to p.
U = 0 S = 400m
aA= ? time of journey from 0 to p= t
S =ut +  aBt2
aBt2
400 = 0 + 0.5 x 5 x ( t - 6 )2
400 / 2.5 = ( t- 6 )2
( t – 6)2 = 160
T - 6 = 12.649
[ t = 18.649 sec ] ----- put in equation (1)
aA= 800 / t2 = 800 / 18.6492 = 2.3 m/s2
[aA= 2.3 m/s2]
VA( at p) = u + at
= 0 + ( 2.3 x 18.649 ) { VA = 42. 9 m/s }
VB(at p) = u + at
= 0 + 5 x ( 18.649 - 6) { VB = 63.245 m/sec }
Two cars A & B travelling at constant speed of 160 kmph car A leads car B by 40 m. at t=0 , both car accelerate at constant rates , at t = 8 sec , car B passes car A & velocity of car A is 220 kmph. Find accelerations of A& B .
→
(1)Car A : -
UA= 160kmph = 160 x 5/18 = 44.45 m/sec.
VA = 200 kmph = 220 x 5/18 = 61.11 m/sec.
T = 8 sec.
We know that ,
V = u + at
VA = uA +aAt
61.11 = 44 .45 + aA x 8
|
aA= ( 61.11 - 44.45) / 8
{ aA = 2.08 m/sec2
As,
S = ut +  at2
at2
SA =UAt +  aA t2
aA t2
= 44.45 x 8 +  x 2.08 x 82
x 2.08 x 82
SA = 422.16 m .
At t= 8 sec ; car B passes car A thus car B has to travel the distance ( SB = 40 + SA) as initially car A was leading by 40 m distance . thus in the same time t = 8 sec ; car B travels ( 40 + SA) distance .
SB = 40 + SA = 40 + 422.16 = 462.16 m.
We know that ,
SB = UB t +  aB t2
aB t2
But initially both cars are having same velocity .
UA =UB= 44.45 m/sec.
462.16 = 44.45 x 8 +  x aB x 82
x aB x 82
462.16 = 355.6 + 32 aB
aB= ( 462.16 - 355.6) / 32
{aB = 3.33 m/s2}
Displacement in nth second :-
( with uniform or constant acceleration )
|
Consider the motion of particle moving along straight line with uniform / constant
Acceleration.
Let the particle start from 0 & moves along ox.
Let u= initial velocity of particle
V= final velocity
a= constant positive acceleration
let- the particle move from 0 to Q in ‘n’ seconds &
the particle move from 0 to p in ‘(n- 1)’ seconds
Sn= Xn = displacement in n seconds
Sn-1 = Xn-1 = displacement in (n-1) seconds
Therefore S = X = Sn- Sn-1 = Xn– Xn-1 = displacement in nth second
n = no. of seconds .
we have equation of motion for displacement,
S = ut + ½ at2
For t= n,
Sn= u (n) + ½ an2
For t = n-1,
Sn-1= u (n-1) + ½ a (n -1) 2
∴ Displacement by particle in nth seconds is given by,
S =Sn- Sn– 1
Or
X =Xn– Xn-1
∴ S = [ un + ½ an2] - [ u(n -1) + ½ a (n -1)2]
∴ S = un + ½ an2 - [ un - u + ½ a ( n2 - 2n + 1)
∴ S = un + ½ an2 - un + u - ½ a ( n2 + 1 -2n )
∴ S = un + ½ an2 - un + u - ½ an2 - ½ a + an
∴ S = ½ an2 + u - ½ an2 - ½ a + an
∴ S = u - ½ a + an
∴ S = u + a ( - ½ + n )
= u + a ( n - ½ )
∴ { s = u + a/2 ( 2n - 1 ) } OR.
{ x = u + a/2 ( 2n - 1 ) }
Distance covered / travelled :
(1) For uni –directional motion along straight line distance covered in
T sec .is given by ,
D = | xt - xo | = | St - So |
(2) for uni – directional motion , i. e. when particle reverses the direction in between 0 & t sec :
Assume that particle velocity is zero at t1 , t2 , t3 ( where t1 , t2 ,t3 lie between 0 & t ) . then ,
D = | xt1 - x0| + | xt2 - xt1 | + |xt - xt2| OR
D = | st1 - s0| + |st2 - st2 | + |st - st2 |
Examples on distance travelled in nth second .
(UAM)
A train starts from rest & move with uniform acceleration along the straight line . it covers 120 m distance in 8th second find uniform acceleration of train .
→
For train , u = 0 , Sth = 120 m.
Using distance travelled in nth second ,
Sth= u + a/2 ( 2n – 1)
S th = u + a/2 ( 2n – 1) ………. Here n =8 sec.
120 = 0 + a/2 (2 x 8 - 1 )
120 = 7.5 a
[ a = 16 m/sec2 ]
A particle covers 90m in 5th sec ; & 140 m in 9th sec of its journey with uniform acceleration find the distance travelled in 15th sec.
→
When n=5 , S = 90m
N = 9 , S = 140 m
∴ using 1st condition
Sth= u + a/2 ( 2n – 1)
A 90 = u + a/2 ( 2 x 5 - 1)
∴ 4.5a + u = a90 …………….(1)
Using 2nd condition ,
Sth = u + a/2 ( 2n-1)
∴ 140 = u + a/2 ( 2 x a – 1)
∴ 140 = u + 8.5 a
∴ 8.5 a + u = 140 -----------(2)
Solving (1) & (2) , we get
[ a = 12.5 m/s2] & [ u = 33.75m/sec.]
S15th= 33.75 + 12.5/2 ( 2 x 15 - 1) = [215 m]
Motion under the gravity
( linear motion with uniform gravitational acceleration)
In this type of motion , the vertical motion of the particle under the influence of constant gravitational acceleration is considered .
G = 9.81 m/s2 ----- gravitational acceleration .
The equations of motions for motion under the gravity are as follows :-
a)when particle motion is towards earth surface
( downward motion of particle )
V = u + gt
V2 = u2 + 2gs
S =ut + ½ gt2
b)when particle motion is away from earth surface against the gravity force
( upwardmotion )
V = u - gt
V2 = u2 - 2gs
S = ut - ½ gt2
Examples on motion with uniform acceleration (UAM)
Motion under the gravity
( g = constant )
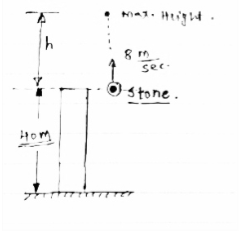
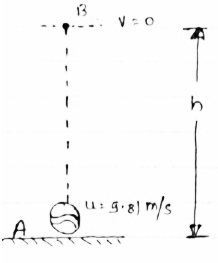
Q.1 From the top of the tower which is 40m high , a stone is thrown vertically upwards with a velocity of 8 m/s. How long does the stone take to reach the ground? Also find out the velocity with which it strikes the ground.
→
Diagram
|
U = 8m/sec.
Tower height = 40 m.
1] consider upward motion of stone
When stone is thrown upward,
Let h = max. height reached by stone.
∴ we have v= u + gt
As stone will stop at max height thus v1 =0
Also g = - 9.81 m/s2 for upward motion.
Thus, equation becomes ;
V1 = u1 – gt1
0 = 8- 9.81 x t1
∴ t1 =8/9.81
T1 = 0.81 sec time required to reach max. height
Now,
Let h = max. height reached by stone during upward motion
∴thus we have, v2 = u2 + 2 as;
Here for upward motion g = - 9.81 m/s2
∴
V12= u1 - 2gh
0 = 82 - 2 x x 9.81 x h
0 = 64 - 19.62 x h
∴ 19.62 h = 64
∴ h = 64/ 19.62
[ h = 3.26 m] -----------above the tower.
(2) now consider downward motion of the stone from the max . height (h) .
Thus in this case , stone will cover ( h + 40 )
Meter distance while coming down .
∴ S2 = h + 40 = 40 + 3.26 = 43.26 m
While starting downward motion ,
Initial velocity = u2 = 0
&final velocity = V2 = ?
We have , V2 = u2 + 2as .
As g = 9.81 m/s2 for down ward motion ,
∴ V22 - U22 = 2gs .
∴ V22 - 0 = 2 x 9.81 x 43.26
∴ V22 = 848.76
∴[V2 = 29.1 m/sec] with this velocity , stone will strike the ground .
Now, let t = time req. for stone to reach ground level from the max height (h).
We have ,
∴ v2 = u2 + gt2
∴ 29.1 = 0 + 9.81 x t2
∴t2= 29.1/9.81
∴[t2 = 2.97 sec ] -------for downward motion .
∴ total time required for stone to reach the ground = time required upward motion + time required for downward motion
T = t1 + t2
T = 0.81 + 2.97
[ t = 3.78 sec.]
Q.(2) A ball is released from a building ( top of building ) of height ‘h’ meter . it comes a vertical distance h/2 during its last second of descend . find the height of building .
→ let h = total height of building
Let the ball is released from the top of the building . from point ‘A’.
B. is the start point at last second of the travel of the ball .
G. is the ground level .
T1 = time required A to B.
|
h/6 = distance covered during last second.
T2 = time required from B to G.
5h/6 = remaining distance covered .
T = total time req. = t1 + t2 = ( t1 + 1) sec.
1) Consider motion from A to B :-
U1 =0 , g = 9.81 m/s2 , S1 = 5h/6
From equation of motion , S = ut + ½ at2
S1 = u1t1 + ½ gt12
Putting the value ,
∴ 5h/6 = 0 + ½ x 9.81 x t12
∴ 5h = 29.43 t12
∴ h = 5.886 t12-----------(1)
2) Consider motion from A to G .
S = ut + ½ gt2
H = 0 + ½ x 09.81 x ( t1+ 1)2
H = 4.905( t1 + 1) 2 -----(2)
Equating (1) & (2) as LHS are same ,
∴ 5.886 t12 = 4.905 ( t1 + 1) 2
∴ = 4.905 ( t12 + 2t1 + 1)
5.886 t12 = 4.905 t12 + 9.81 t1 + 4.905
0.981 t12 + 9.81 t1 - 4.905 = 0 ----------------solving this …
[t1= 10.477 sec .] ∴ h = 5.886 t12 = [ 646.09 m]
∴ [ height of building = h = 646.0 m]
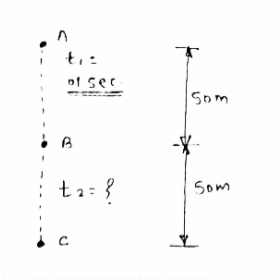
Q.3 A particle freely falls 50 m under gravity in a certain second . calculate the time required to cover next 50 m.
Consider particle freely falls from point
A to B (50m) in 1 sec .
∴ t1 = time req. from A to B .
T1 = 1 sec.
|
Let particle covers next 50 m i.e.
From B to C in time t2 sec .
1) consider motion from A to B.
U1 = 0 , t1 = 01 sec . , S1 = 50m.
Using equation of motion,
∴ s1 = u1t1 + ½ g t12
∴ 50 = u1 + 9.81 x 12
∴ st = u1 + 4.905
∴ u1 = 45.095m/sec
V1 = velocity at point B - is given by ,
V1 = U1 + gt1
= 45.095 + (9.81 x 1
V1 = 54.905m/sec
2) consider the motion from B to C:-
At the start point of motion i.e. at B,
V1 = 54.905 = u2
& s2 = 50 m(from B to C).
Thus,
A stone is thrown vertically downwards from the top of a 49m high tower. A second later one ball is thrown vertically upward from the ground with a velocity of 12.5m/sec. at what distance above the ground will both the stones cross each other?
|
Let A – point from which stone is thrown
G - ground level (ball is thrown up)
C - crossing point of stone & ball
Let d = distance covered by stone from
A to c (crossing point)
(49-d) = distance covered by ball from ground to crossing point ‘c’
T = time taken by stone to reach from A to C
(T -1) = Time taken by ball to reach from G TO C.
(1) Consider motion from A to c (for stone) → u =0
S =ut + ½ gt2
D = 0xt + ½ x 9.81 t2
∴ d = 4.905 t2 ………(1)
(2) consider motion from G TO C
S =ut – ½ gt2
(49-d) = 12.5t x (t -1) – ½ x 9.81 x (t-1)2
= 12.5 t – 12.5 – 4.905(t2 -2t + 1)
49 –d = 12.5 t - 12.5 -4.905t2 + 9.81 t - 4.905
∴ d= 4.905 t2 - 22.31t + 66.405 -------(2)
Equating (1) & (2)
∴ 4.905 t2 = 4.905 t2 - 22.31 t + 66.405
∴ 22.31 t = 66.405
∴ [ t = 2.37 sec] ≈ 3sec
∴ d = 4.905 x t2 = 4.905 x 32
∴[d = 44.14 m]
∴ (49 – d) = 4.85 m. -------[ both objects cross each other at 4.85m above ground.
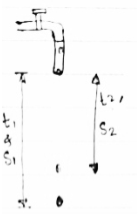
Water drops from a tap at the rate of five drops per second . determine the vertical separation between two conservative drops after the lower drop has attained a velocity of 7 m/sec.
→
Rate of droplets = 5 drops per second .
∴time difference between two consecutive drops = 1/5 = 0.2 sec.
Let us assume that , 1st or lower drop attains the velocity of 7 m/sec after ‘t1’ sec.
Then 2nd drop will take (t1 - 0.2) sec. = t2
|
1)consider first drop & its motion .
U1 = 0 , v1 = 7 m/sec
∴ v1 = u1 + gt1
7 = 0 + 9.81 xt1
∴ [ t1 = 0.714 sec. ]
During this time , distance travelled by 1st droplet will be ,
S1 = u1t1 + ½ gt12
= 0 + ½ x 9.81 x 0.714 2
[ S1 = 02.497 m.]
2)consider 2nd drop & its motion .
∴ time for 2nd drop = t1 - 0.2
= 0.714 - 0.2
T2 = 0.514 sec.
∴ distance travelled by 2nd drop in 0.514 sec.
S2 = u2t2 + ½ gt22
= 0 + ½ x 9.81 x 0.514 2
[ S2 = 1.296 m ]
The vertical separation between two drops
= S1- S2
= 2.497 - 1.296
= 1.201 m.
Q.6 A ball is projected vertically upward with a velocity of 9.81 m/s determine maximum height travelled by the ball , velocity at which it strikes the ground & total time of journey .
|
A)Consider the motion of ball from A to B :-
U1 = 9.8 m/s
V1 = 0 m/s
S1= h = max . height travelled by ball .
T1= time taken by ball for motion from
A to B.
Using equation of motion V 2 =U2 + 2as
∴V12 = U12 - 2gs
∴ 0 = 9.812 - 2 x 9.81 x h
∴ h = 9.812/ 19.62
∴[ h = 4.905 m ] --------- max. height reached .
Now using
S1 = h = U1t1 - ½ g1t12
∴4.905 = 9.81 t1 – 0.5 x 9.81 x t1
∴ 4.905 t12 - 9.81 t1 + 4.905 = 0
Solving
[ t1 = 01 sec.] -----------for upward motion of ball.
2) consider downward motion of ball ,
U2= 0 , V2 = ? , S = h = 4.905 m
∴
Using V2 - U2 = 2as
V22 - U22 = 2gs2
V22 - 0 = 2 x 9.81 x 4.905
∴ [V2 = 9.81 m/s ] ---------------- with this velocity , ball will strike the ground .
Now using
V2 = U2 + gt2
9.81 = 0 + 9.81 t2
∴ [ t2 = 01 sec.]
Total time of journey = t1 + t2 = 2 sec.
We know , velocity of a body is
V = (ds/dt) OR V =( dx / dt)
&
Acceleration ,
A = dv / dt | a = dx / dt
= d/dt ( ds/dt) | = d / dt (dx / dt)
A = d2s/ dt2 | a = d2x/ dt2
= V. dv/ds | = V.dv/dx
A body or particle sometimes moves along the straight line with variable acceleration .
This variable acceleration may be the function of time or position or velocity .
(1) When acceleration is function of time (t) [ a= f(t) ]
a= dv /dt ) = f (t)
∴ dv = f(t) dt
Integrating both sides , we got
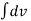 =
= 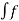 (t) dt
(t) dt
This will give us equation for velocity as a function of time
V = f (t)
Velocity,
V = ds / dt = f (t)
∴ ds = f (t) dt .
Integrating above equation we get S ( displacement ) in terms of ‘t’.
While solving the problems on variable acceleration , following cases will arise :-
(1)Given equation of motion is in terms of displacement (s) & time (t)
S = f (t) or x = f (t)
Differentiating both sides will give , ( w.r.t. time t)
V = ds / dt = f(t) or V = dx / dt = f (t)
Again differentiating above equation , w.r.t. (t)
A= dv /dt = d2s / dt2 = v . dv/ds = f (t) OR ∴ a= dv/dt = d2x/dt2 =v. dv/dx = f (t)
(2) given equation is in terms of acceleration (a) & time (t) .
A = f (t)
Integrating once will give us velocity . &
Integrating again will give us the displacement .
(3) given equation is in terms of acceleration (a) & displacement ( x or s)
A = f (s) or a = f(x)
Integrating once will give us velocity equation
Integrating twice will give the equation of motion for displacement
(4) given equation is in terms of velocity (v) & time (t)
V = f (t)
Integrate above equation to get displacement .
Differentiate above equation to get acceleration .
( in all above cases , use given condition to find the constants of integration .)
Examples based on variable acceleration :-
(equation in terms of s & t or x & t – given)
1 ) the position of a particle which moves along a straight line is defined by the relation S= t3 - 6t2 - 15 + 40 , where S is in meters and t in sec ;
Determine :- a) time at which velocity will be zero .
b) position & distance travelled by particle at that time .
c) acceleration at that time .
d) distance travelled by particle from t= 4 sec to t= 6sec
→ s = t3 - 6t2 - 15t + 40
Differentiating w.r.t. time ‘t’
Ds/dt = 3t2 - 12t - 15
∴ v = ds/dt = 3t2 - 12 t - 15
Again differentiating w.r.t. time ‘t’
a= dv/dt = d2s/ dt2 = 6t -12
a ) time at which velocity will be zero
for , V =0
∴ v = 3t2 - 12t - 15
∴ 0 = 3t2 - 12t -15
Solving the equation
[ t = 5 sec]
B ) t = 5 sec. at this time ,
Displacement will be ,
∴ Ss= t2 - 6t2 – 15t +40
∴ Ss =( 5)2 - ( 6 x 52) - (15 x 5 ) + 40
∴ Ss = -60 m.
At t = 0 sec ; displacement will be ,
S0 = t2 - 6t2 – 15t + 40
∴ S0 = 40 m.
2 ) the motion of particle is defined by x = t3 - 6t2 - 36 t - 40 . in meter . determine (1) when the velocity is zero . (2) velocity , acceleration & total distance travelled when x = 0 .
→given ,
X = t3 - 6t2 - 36t - 40
Differentiating w.r.t. t , we get ,
∴ v = dx /dt = 3t2 – 12t - 36
Again differentiating w.r.t. ‘t’
∴ a= dv/dt = d2x/ d2t = 6t – 12
( 1) when the velocity is zero .
For , v= 0 ;
V = 3t2- 12t - 36
0 = 3t2 - 12t - 36
Solving above equation , we get
[ t = 6 sec.]
( 2) velocity , acceleration & total distance travelled at x=0 .
For x = 0 , x = t3 - 6t2 – 36t – 40
O = t3- 6t2 – 36t -40
Solving above equation, we get
T = 10sec.
∴ velocity (for t =0)
V10 = 3t2 – 12 t – 36
=(3x102)- (12x10)-36
V10 = 144m/sec
∴ acceleration (for t = 10)
A = 6t – 12
= (6x10)-12
A = 48m/sec2
Distance travelled = |x10 – x6| + |x6 –x0|
∴ x10 = 103 – ( 6 x 102)- ( 36 x 10 ) – 40
= 1000 – 600 – 360- 40
X10 = 0m
∴ x6 = 63 – (6x62) –(36x6) – 40
X6 = -256m
∴ x0 = 03 – 6 x 02 -36x 0 -40
X0 = -40 m
∴ distance travelled = |0 – (-256)| + |-256 –(-40)|
= 256 + 216
= 472m
Distance travelled = |ss- s0|
= |-60-40|
=100m
(c) acceleration at t = 5 sec
A = 6t - 12
= (6 x 5) -12
A = 18 m/s2
(d) distance travelled from 4 to 6 sec
As at t = 5sec , v = 0
Thus,
Distance travelled = distance travelled from 4 to 5 sec + distance travelled from 5 to 6 sec.
= |s5 – s4|+ |s6 – s5|
∴at t = 6, s6 = 63 - (6 x 62) – (15 x 6) + 40
=-50m
At t =4, s4 = 43 - (6 x 42) – (15 x 4 ) + 40
= -52m
Distance travelled = | -60 – (-52)| + |-50 – (-60)|
= 8+10
= 18m
a small part in the mechanism travels on straight line such that its position is x =t4 - 10t2 + 24 where x is in & t in sec determine (a)when velocity is zero (b) when acceleration is zero (c) minimum speed reached by partical (d) distance travelled in 3 sec. (e) expression of x in terms of a.
→
X= t4– 10 t2 + 24
∴differentiating w.r.t “t”
V = dx/dt = 4t3 – 20t
Again differentiating w.r.t “t”
A = dv/dt = 12t2 – 20
(a) When velocity is zero (v=0)
∴ v = 4t3 – 20t
∴ 0 = 4t3 - 20t
∴ 0 = t (4t2 - 20)
∴ t = 0 and 4t2 - 20 = 0 solving this equation
T = 2. 23sec
∴ velocity is zero at
T = 0 & t = 2.23sec
( b) when acceleration is zero i.e. (a=0)
∴ a = 12t2 - 20
∴ 0 = 12t2 - 20
Solving this equation
T = 1.29 sec
∴ t = 1.29 sec, acceleration is zero
(c) minimum speed reached by particle
∴ minimum speed will be reached when dv/dt =0
i.e. a=0 & for a = 0 t = 1.29 sec
thus minimum speed will be reached at t 1.29 sec
∴ |VT = 1.29| = |4t3 -20t|
= |4 x 1.293 – 20 x 1.29|
V1.29 = 1%21 m/sec
(d) distance travelled in 3 sec
D = |x3 - x2.23| + |x2.23 - x0|
∴ x3= 34 – 10 x 32 +24
∴ x3 = 15m ……..position at t = 3 sec
∴ x2.23 = 2.234 - 10 x 2.232 +24
∴ x2.23 = -0.99m ……. Position at t = 2.23sec
&
X0 = 04 - 10 x 02 +24
X0 = 24m ……position at t = 0sec
∴ distance travelled = | 15 – (-0.99)| + |(-0.99)-24|
= 15.99 + 24.99
= 40.98m
(e) relation x in terms of a
∴ we have a = 12t2 -20 ∴ t2 = a =20/12
Substituting this value in the equation of x we get,
∴ x = t4 - 10t2 + 24
∴ x = ( a= 20/ 12 )2 - 10 ( a + 20 / 12) + 24
∴ x = a2 + 40a + 400/ 144 - 10/12 (a +20 ) +24
∴ x = a2 + 40a + 400/144 - 10( a+20 )/12 +24
∴ 144x = 144 (a2 +40a + 400)/144 - 14 x 10 (a + 20)/12 + 24 x 144
∴ 144x = a2 + 40a + 400 - 120a - 2400 + 3456
∴ 144x = a2 - 80a + 1456
Example on motion with variable acceleration (equation in terms of a & t i.e. a = f(t) is given)
a particle moves along straight line with an acceleration a = (4t2 - 2) where a is in m/s 2& t is in se. when t = 0 the particle is at 2m to the left of origin & when t =2sec particle is at 20m to the left of origin determine line position of particle at t = 4sec.
→
Given a = 4t2 - 2 When t = 0 , x = -2m T = 2, x -20m ∴ a = dv/dt = 4t2 - 2 ∴ dv = ( 4t2 - 2 )dt ∴ ∴ V = 4t2/ 3 - 2t + c1 ∴dx/dt = 4t3/ 3 - 2t + c1 ∴ dx = [ 4t3 / 3 - 2t + c1 ] dt ∴ ∴ x = t4/3 - t 2 + c1 t + c2 Now , at t = 0 , x = -2 | at t = 2 , x = -20 | ∴ -20 = 24/3 - 22 + c1 x 2 - 2 ∴ -2 = 0 -0 + 0 + c2 | ∴ -20 = 16/3 - 4 + 2 c1 -2 ∴ [ c2 = - 2 ] | ∴ [ c1 = -9.67]
Thus , x = t4/3 - t2 - 9.67t -2 ∴ at t= 4 , ∴ x = 44/ 3 - 42 - 9.67 x 4 - 2 ∴ x = 256/3 - 16 - 38.68 -2 [ x = 28.65 m]
|
2 ) The acceleration of a point moving along a straight line is given by the equation a = 12 t - 20 . it is known that its displacement s= -10 m at time t=0 & s = + 10m at time t = 5 sec . derive equation of motion .
→
a = 12 t - 20, given condition : 1) s = -10 m at t= 0 sec. 2) s = 10 m at t = 5 sec ∴ we know that , ∴ a= dv/dt = 12t - 20 ∴ dv = ( 12 t – 20) dt Taking integration ∴ ∴ v = 6t2 - 20 t + c1 ∴ ds/dt = 6t2 - 20t + c1 ∴ ds = ( 6t 2 - 20t + c1 ) dt Integrating again ∴ ∴ s = 2t3 - 10 t2 + c1 t + c2 Now using given conditions , 1) s = -10 & t= 0 2) s = 10 & t = 5 ∴ -10 = 2 x 103 - 10 x 0 2 + c1 x 5 - 10 ∴ 10 = 250 - 250 + 5c1 - 10 ∴ 10 +10 = 5c1 ∴ c1 = 20/5 [ c1 = 4]
|
Thus equation of motion is [ s = 2t3 - 10t2 + 4t - 10 ]
Examples based on motion with variable acceleration
( equation in terms of a & x is given i.e. a f (x))
1 ) A particle oscillates between the points x= 40 mm & x = 160 mm with an acceleration a = k (100 – x) where k is constant . the velocity of particle is 18 mmm/sec when x = 100mm & is zero at both x = 40 mm & 160 mm. determine 1) value of k . 2) the velocity when x =120 mm.
→ a = k (100 – x) ------given relation
Given conditions are : 1) v = 18 mm/s at x = 100mm
2) v = 0 mm/sec at x = 40 mm
3) v = 0 mm/s at x = 160 mm
∴
A= v.dv/dx = k (100 - x)
∴v. dv = k ( 100 – x ) dx
∴  =
=  (100 – x) dx -------------- integrating in this
(100 – x) dx -------------- integrating in this
∴ v2/2 = k ( 100x - x2/2) + c1
Now using conditions 1) & 2)
∴ 182/2 = k (100 x100 - 1002/2 ) + c1 | 0 =k (100x40 – 402/2)+c1
∴162 = 5000 k + c1 | 0 = 3200k +c1
∴ 162 = 5000k - 3200k | ∴ c1= -3200k
∴ 162 = 1800k
∴ [k=0.09] & c1 = -3200 x 0.09
∴ [ c1 = -288]
The equation of velocity becomes ,
∴ v2/2 = 0.09 ( 100x - x2/2 ) -288
∴ v2 = 0.18 ( 100x - x2/2 ) - 576
Now for x = 120 mm ,
V2 = 0.18 ( 100 x 120 - 120 x120 / 2 ) - 576
[ v = +- 16.97 mm/sec
2 ) A particle travels in a straight line with accelerated motion such that a = - kx , where x is the distance from starting point . find constant k if for x = 2m , velocity is 4 m/sec . and for x = 3.5 m , the velocity is 10 m/sec . also find x when the velocity is zero.
→given data : conditions given :
A = -kx. 1 ) x = 2m , v = 4 m /sec .
2 ) x = 3.5 m , v = 10 m/sec .
Find 1) k & 2) find x for v= 0
∴ a= v.dv/dx = - k . x
∴ v.dv = - kx dx .
∴  dv = - k
dv = - k 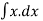
V2/2 = - k x2/2 + c1
Using 1 st condition , x = 2 , v = 4 m/sec .
∴ 42/2 = -k x 22/2 + c1
∴ 8 = -2k + 4 --------1)
Using 2nd condition x = 3.5 , v = 10
102/2 = -k x 3.5 2/2 + c1
50 = - 6.125 k + c 1 --------2)
Solving equation 1) & 2) we get
[ C1 = -12.36] & [ k = -10.18]
∴equation of velocity is v2/2 = 10.18 x2/2 - 12.36
∴ v2 = 10.18 x2 - 24.72
For , v=0, 0 = 10.18 x2 - 24.72
∴ solving above equation for x.
[ x = 1.558 m]
Example an motion with variable acceleration
( equation is given in terms of v & t I .e. v = f(t) )
A particle moves along a straight line with velocity v = 3t2 – 6t (in m/sec.) if it is initially at origin . determine the average velocity , average speed & distance travelled during interval 0≤ t ≤ 3.5 sec
→ given v = 3t2 - 6t
If t = 0 then v =0 & also x =0
∴v = 3t2 - 6t
∴v = dx/dt = 3t2– 6t
∴ dx = (3t2 – 6t) dt
Integrating above equation ,
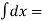 ∫(3t2 – 6t) dt
∫(3t2 – 6t) dt
X = T3– 3T2 + c1
From the condition t =0 ,x =0
∴ 0 = 03 – 3x 0 + c1
∴ c1= 0
∴ x= t3 - 3t2
(1) Average velocity = change in position/ time interval
Vavg= x3.5 - x0/ 3.5- 0
∴ x3.5 = 3.53 – 3 x 3.52 = 6.125m
X0 =03 - 3 x 0 = 0m
∴ Vavg= 6.125 - 0/ 3.5 -0 = 1.75m/sec
(2) Average speed
To find avg. speed always check where the velocity is zero & then find distance travelled.
∴ v = 3t2- 6t
∴ 0 = 3t2 – 6t
Solving this equation,
T=0 & t = 2 sec
Distance travelled = |X3.5 – X2 | + |X2 – X0 |
∴ X3.5= 6.125m
∴ X0= 0m
X2= 23 - 3 x 22
= 8 – 12
X2 = -4m
∴thus, distance travelled Is,
D = |6.125 -(-4)| + |-4 -0|
= 10.125 + 4
= 14.125m
∴ avg. speed =distance travelled/3.5 = 14.125/3.5
∴ avg. speed = 4.08m/sec
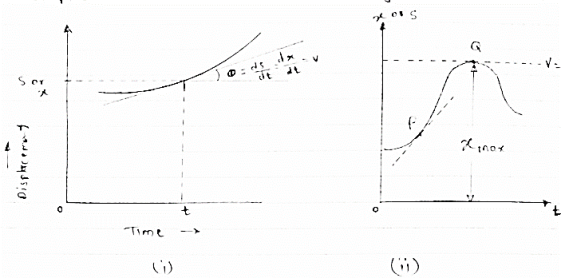
MOTION DIAGRAM (MOTION CURVES):-
it is a graphical representation of displacement velocity acceleration with time.
(1) Displacement - time curve : (x –t diagram)
(2) |
(3)
This diagram represents position of particle w.r.t to time here time is taken on x axis & displacement (s or x) is taken on y axis
Slope x t diagram at any point represents the velocity at the instant
∴at any instant t (time)
Velocity is given by v = ds/dt = dx/dt
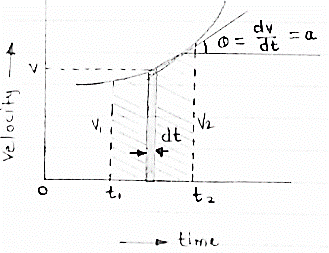
(2)velocity time curve: [ v - t diagram ]
|
this diagram represents velocity of particle w.r.t. time here velocity is taken on y axis & time on x axis
(a)the slop of v – t diagram represents acceleration at that instant
∴a = dv/dt
(b)area under the curve (v –t curve)represent change in displacement (x or s)between two instant of time
∴let us select elementary trip betweent1 & t2.
∴ the area of strip da = v x dt
Area bounded between t1 &t2can be find out by integrating area of elementary strip.
∴da = v. dt
∴ ∫da = ∫v.dt
∴ A =
But v=dx/dt b ∴ v.dt = dx
∴ A = 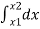 =[
=[
∴ A = area between (t1 & t2 ) = x2 - x1
(3) acceleration - time diagram (a –t curves):
|
This representation acceleration of particle w.r.t. time ‘t’. acceleration is plotted on y axis & time is plotted on x axis.
The slope of the curve representation jerks J = da/dt
The area under a- t diagram between two instant of time (t1 & t2) represent change in velocity
Let us consider an elementary strip
∴ area of strip da = na.dt
∴ total area a = 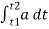 but a = dv/dt∴ a. dt = dv
but a = dv/dt∴ a. dt = dv
∴ a = 
∴ area a= v2 - v1
The position co ordinate (x) is directly found out from the following moment equation (from a – t diagram)
X1 = x0 + v0 t + mt
Where,
Xt= position of particle at time ‘t’
X0 =initial position of particle
V0 = initial velocity of particle
Mt = moment of area under a - t diagram about the instant t.
Velocity - displacement diagram (v -x)
|
Here plot or graph of velocity (on y axis ) & displacement on (x axis) is drawn.
If a normal is drawn to the tangent on curve the subnormal on x axis represents the acceleration
Let pr is the normal drawn at p
The subnormal = pq.tanθ
=v.tanθ
= v.dv/dx
= a
∴ a = V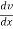
∴ Acceleration = velocity x slope of v- x diagram
Numerical on motion diagram
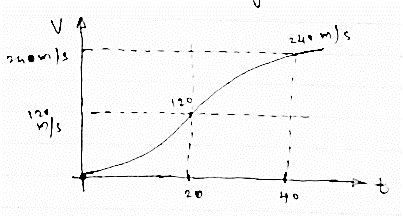
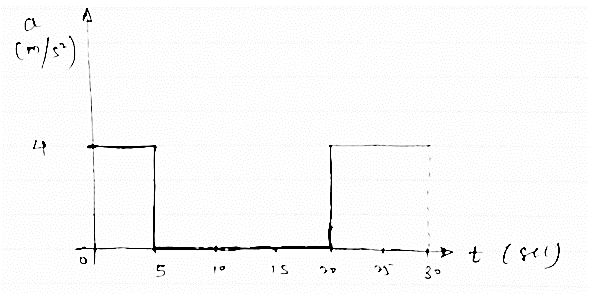
the acceleration versus time for a particle moving along x axis is given in the figure given below. The time interval is 0 to 40 sec for some time interval plot
(1) V-t diagram (2) x – t diagram (3) also find max speed attained & max distance covered
Diagram
|
We know that,
Change in velocity = area under a-t diagram from the given a – t diagram
∴at T = 20sec
V20 - v0 = 1/2 x 20 x 12
V20- v0 = 120 m/sec
But at T =0 , v0 = 0
∴ 20= 120m/sec
Now,
At t =40 sec
∴ v40- v20= ½ x 20 x 12 = 120
∴ v40 = 120+v20
∴ v40 = 240m/sec
Thus v -t diagram will be as follows
|
Now from above v - t diagram
Change in displacement = area under v- t diagram
At t=20sec
X20 - X 0 = 1/3 x 20x 120 = 800m
As (X0 = 0 at t = 0 )
∴X20 = 800m
At t =40sec
X40 - X20 = (20x 120) + (2/3 x20 x120)
X40 = 2400+1600+ X20
X40 = 24001600+800
X 40= 4800m
∴ x -t diagram will be as follows
|
Max speed attained = 240m/sec
Max distance travelled = 4800m
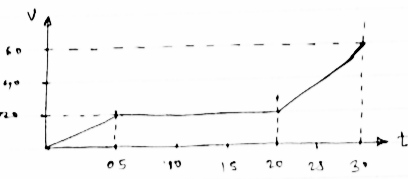
The figure below shows v.t graph of jet plane travelling along runway construct x –t & a –t graph for the motion of jet plane the plane starts from rest.
Diagram
|
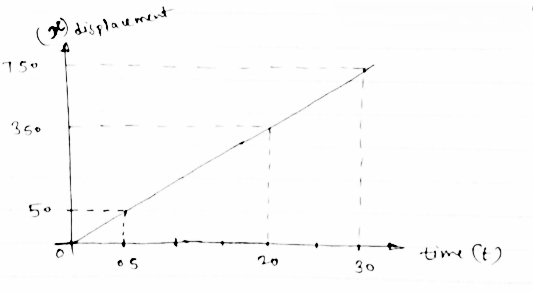
(1) X- t diagram;- ∴ change in displacement = area under v-t diagram
At t =0 , x=0
At t=5sec
X5 -X0 =1/2 x 5 x20 =50
∴ X5 =50 - X0
X5 =50m
At t =20 sec
∴ X20 - X5 = 15 x 20 = 3000
∴ X20 = 300 + X5 = 300 +50 =350m
At t = 30 sec
∴ X30 -X20 = (10X20) + (1/2 x 10 x 40)
= 200 + 200
X30 = 400 + 350
X30 = 750M
∴ THIS X – T DIAGRAM IS BELOW
|
Now,
From given v- t diagram ,
Slope of v - t diagram = acceleration
At t=0 slope a = 20/5 = 4m/s2
Before t = 5 , slope a = 20/5 =4m/s2
After t =5 , slope a = 0 as v constant
Before t = 20 , slope a = 0
After t 20 , slope a 40/10 = 4m/s2
At t = 30,
Slope a =40/10= 4m/s2
∴a -t diagram is drawn below
|
When a particle moves along a curved path, then motion of the particle is said to be curvilinear.
Basic terminology used to describe curvilinear motion: -
- Position vector: - (
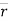 )
)
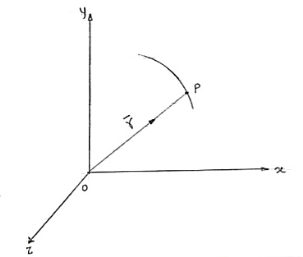
- Consider that particle is moving along the curve as shown in figure.
|
b. Let ‘P’ is the position of particle at any time instant ‘t’.
c. Let we have fixed reference axes x,y,z as shown.
d. The line ‘OP’ represents the position of particle &it is known as position vector of particle at time ‘t’.
 position vector
position vector 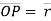
e. 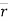 = xi + yj + zk and
= xi + yj + zk and
 - magnitude of position
- magnitude of position
2. Displacement and distance:
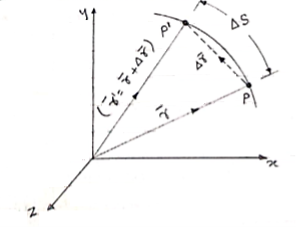
- Consider that particle is moving along the plane curve P-P’ as shown in figure.
|
- Let particle is located at point P at time instant ‘t’.
Position of particle at point P is given by vector 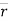 . Now after time (t + ∆t), let particle is moved to a new position P’. This position of particle is given by the vector (
. Now after time (t + ∆t), let particle is moved to a new position P’. This position of particle is given by the vector (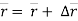 )
)
- The vector joining P & P’ is ∆
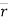 . (dashed line)
. (dashed line)
∆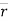 = change of position of particle during the time interval ∆t.
= change of position of particle during the time interval ∆t.
∆ = displacement of particle.
= displacement of particle.
- The distance travelled by the particle along the curve from point P to P’ is ∆s. this is measured along the curved path & is scalar quantity.
3. Velocity :
In above figure ∆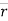 = displacement vector
= displacement vector
∆r = displacement of particle (magnitude).
∆t = time taken by particle to move from P to P’.
Avg. velocity = 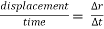 = vavg.
= vavg.
- When the time interval approaches to zero, ∆t → 0.
Instantaneous velocity at P will be,
V = 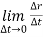
V = 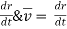
Speed = 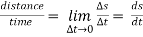
4. Acceleration: -
Avg. acceleration a = 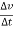
For very small interval of time ∆t → 0
Thus a =  &
&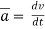
The acceleration at point P = 
(Instantaneous acceleration)
Co-ordinate systems in curvilinear motion: -
There are 3 different co-ordinate systems that are used to describe the motion of particle along the curved path.
- Rectangular co-ordinate system
Also known as Cartesian co-ordinate system
2. Normal & tangential co-ordinate system.
Also known as path variables or path co-ordinates
3. Radial & transverse co-ordinate system.
Also known as polar co-ordinate system.
1) Rectangular / Cartesian co-ordinate system
If particle is moving along curved path, we can split its motion into x, y, z directions as an independently performing rectilinear motion.
|
- In the figure (i) above,
Consider the particle moving along the curve & at any instant ‘t’, it is at point P(x, y,z). Thus, position vector for particle at P is
 …………… Position vector
…………… Position vector
Where x,y,z are the functions of time (t).
To find velocity & acceleration of particle, let us differentiate position vector 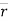 w.r.t. ‘t’ (time)
w.r.t. ‘t’ (time)
 = xi + yj + zk
= xi + yj + zk
Taking derivative,
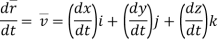
 vxi + vyj + vzk ……………. velocity vector
vxi + vyj + vzk ……………. velocity vector
Where,
vx = 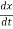 , vy =
, vy = 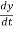 & vz =
& vz = 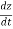
vx, vy, vz = x,y,z component of velocity respectively.
Magnitude of velocity = v =  for space curve
for space curve
v = 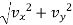 for plane curve
for plane curve
Direction of velocity = tan α = 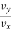 for plane curve
for plane curve
Now differentiating velocity w.r.t. time
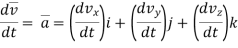
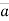 = axi + ayj + azk ------acceleration vector
= axi + ayj + azk ------acceleration vector
Where
ax = 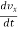 ----------- x component of acceleration
----------- x component of acceleration
ay =  ----------- y component of acceleration
----------- y component of acceleration
az =  ----------- z component of acceleration
----------- z component of acceleration
magnitude of acceleration
a =  ----- for space curve
----- for space curve
a =  ------for plane curve
------for plane curve
direction of acceleration
tan β =  -----for plane curve
-----for plane curve
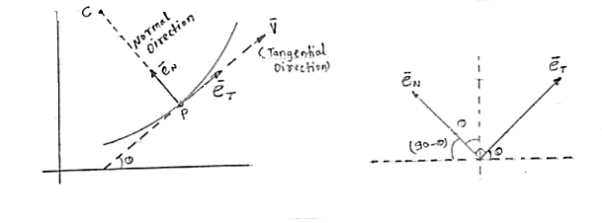
2) normal & tangential co-ordinate system: - [path variables]
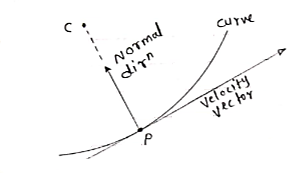
- We know that, velocity of particle is always tangential to the path along which it is moving.
|
(consider a particle moving along curve & is located at point P at any instant ‘t’)
So the tangent drawn at that point (at point P) represents the tangential direction. &
The direction which is perpendicular to the velocity vector (or tangent at P) & passing through center of curvature is known as normal direction.
|
- Let us consider the particle moving along a curve contained in the plane as shown in figure above.
Let P is the position of the particle at a given instant. Now, let us attach unit vector  at point P.
at point P. 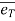 is along tangential direction
is along tangential direction 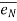 is along normal direction.
is along normal direction.
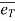 = unit vector along tangential direction
= unit vector along tangential direction
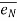 = unit vector along normal direction.
= unit vector along normal direction.
- Unit vectors can be written as
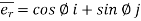 &
& =
= 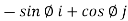
Differentiating above equation w.r.t. Ø
We get,

 --------- (2)
--------- (2)
- Velocity components
As the velocity is always tangential to the path along which partial moves, Then,
Tangential component of velocity is equal to velocity itself and normal component will be zero.
vT = v
vN = 0
the velocity vector of particle is tangent to path.
It will be
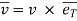
- Acceleration of particle
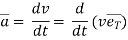
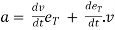 --------(3)
--------(3)
But  by double chain rule
by double chain rule
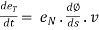 ----------(4)
----------(4)
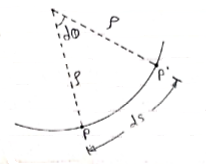
- Now let us find the value of
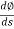
|
Consider particle moving along curve is at P at time t. Then after small time interval ∆t, particle attains new position at P’. during this it covers ‘ds’ distance along the curve.
Let C = center of radius of curvature.
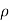 = radius of curvature of curved path
= radius of curvature of curved path
- Then arc length = radius × angle subtended by arc
ds = 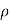 × dØ
× dØ

Putting above value in equation (4), we get,

Putting this value in equation (3)


 --------acceleration vector
--------acceleration vector
Where,
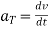 & -----tangential component of acceleration
& -----tangential component of acceleration
 ----------normal component of acceleration
----------normal component of acceleration
Magnitude of acceleration (total)
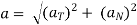
Direction of total acceleration is,
tan α = 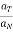 where α = angle made by acceleration with normal direction
where α = angle made by acceleration with normal direction
- aN is always directed toward center of curvature.
- aT reflects the change in speed of particle.
- aN reflects the change in direction of motion.
- When
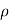 become infinity at inflection point then aN = 0
become infinity at inflection point then aN = 0
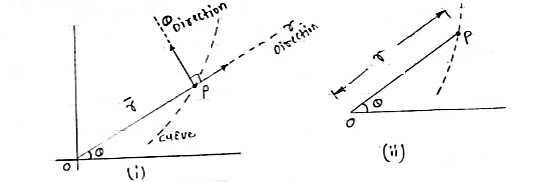
3) Radial & transverse co-ordinates system [Polar co-ordinates]
|
- Consider a particle moving along the curve & located at point P at any instant ‘t’.
- To define the position of the particle, we can say that P is located at a radical distance r from origin & at an angular measurement Ø to the radial line. (fig 2)
- Thus, the direction along the position vector
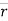 is called as radial direction (r) and the direction which is perpendicular to the position vector
is called as radial direction (r) and the direction which is perpendicular to the position vector  is called as transverser direction (Ø). (fig 1)
is called as transverser direction (Ø). (fig 1)
- Let particle is moving along a curve & is located at point P at any time instant ‘t’. let r is radial distance &Ø is angle made by radial direction.
- Let us attach unit vector
 at point P along radial direction &
at point P along radial direction &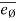 at point P along transverse direction.
at point P along transverse direction.
- Unit vector
 defines radial direction & unit vector
defines radial direction & unit vector 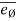 defines transverse directions.
defines transverse directions.
- Unit vectors can be written as,
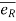 = cosØ i + sinØ j and
= cosØ i + sinØ j and  = - sinØ i + cosØ j
= - sinØ i + cosØ j
Differentiating above vectors with ‘Ø’.
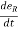 = - sinØ i + cosØ j and
= - sinØ i + cosØ j and 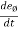 = - cosØ i – sinØ j
= - cosØ i – sinØ j
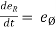 ------(1) and
------(1) and  = - (cosØ i + sin Ø j)
= - (cosØ i + sin Ø j)
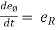 ------(2)
------(2)
Now by chain rule,
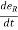 =
= 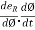 and
and  =
= 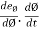
Let  = time derivative of Ø ; then,
= time derivative of Ø ; then,
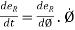 and
and 
 and
and 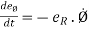 -----------(3)
-----------(3)
Velocity component: -
We know that,
Position vector = magnitude × unit vector along the direction

Differentiating this w.r.t. time,

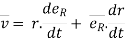
 by using equation (3)
by using equation (3)
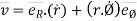 where
where 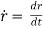
 = (vR)
= (vR) + (vØ)
+ (vØ)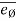 ………where
………where
Radial component of velocity = vR = 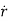 =
= 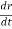
Transverse component of velocity = vØ= r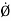
Resultant velocity or total velocity,
v = 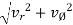 ---------magnitude
---------magnitude
direction of velocity, tan α =  where
where
α = angle made by velocity with radial directions.
Acceleration component: -
We know that,
Acceleration vector,
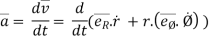
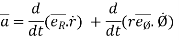
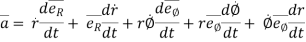
= 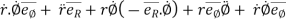
= 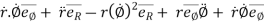
= 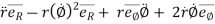
= 
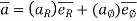 ---------acceleration vector
---------acceleration vector
Where,
 = radial component of acceleration =
= radial component of acceleration = 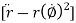
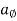 = transverse component of acceleration =
= transverse component of acceleration = 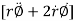
Resultant or total acceleration =  ------magnitude
------magnitude
tan β =  -----------direction of acceleration
-----------direction of acceleration
where β = angle made by acceleration with radial direction.
Speed case of curvilinear Motion
(Circular motion)
For the motion in circular path -: (r is constant)
- Radial component of velocity = vR = 0
- Transverse components of velocity = v = vØ = r

- Radial component of acceleration =
 = -r
= -r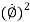
- Transverse component of acceleration =
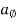 = r
= r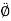
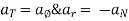
Radius of curvature
- When rectangular components of velocity & acceleration are known,
Radius of curvature = 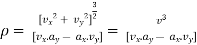
2. When 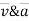 are known, Then,
are known, Then,
- Magnitude of
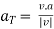
- Magnitude of
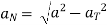
- Radius of curvature =
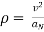
- When path equation y = f(x) is given,
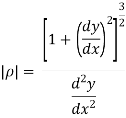
Numerical on rectangular co-ordinates/equation of motion in Cartesian co-ordinates
Que 1. A particle moves along a curved path given by the relation y = 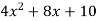 starting with initial velocity
starting with initial velocity 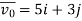 . If vx = constant, determine of vy& ay at x = 3m. Also determine the magnitude of velocity and acceleration.
. If vx = constant, determine of vy& ay at x = 3m. Also determine the magnitude of velocity and acceleration.
→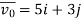 so, vx0 = 5m/sec and vy0 = 3m/sec
so, vx0 = 5m/sec and vy0 = 3m/sec
y = 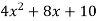
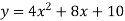
Differentiating w.r.t. ‘t’
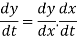
vy = (8x + 8)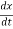
= (8x + 8)vx
vy = 8x.vx + 8vx
again differentiating w.r.t. ‘t’

 vx
vx
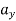 = [0 + 8vx + 0]vx
= [0 + 8vx + 0]vx
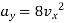
Now at x = 3m,
Vy = 8.x.vx + 8vx
= (8 × 3 × 5) + (8 × 5)
= 120 + 40
= 160 m/sec
(as vx = constant)
(vx0 = vx = 5 m/sec)
 = 8.vx2
= 8.vx2
= 8 × 52
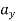 = 200 m/s2
= 200 m/s2
 = 0
= 0
Magnitude of velocity
v = 
v = 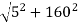
v = 160.07 m/s
magnitude of acceleration
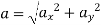
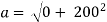
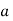 = 200 m/s2
= 200 m/s2
Que 2. A particle along the path 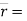 (8t2)i + (t3 + 5)j. where ‘t’ is in seconds. Determine the magnitude of particle velocity and acceleration when t = 4 sec. find the equation of path, y = f(x).
(8t2)i + (t3 + 5)j. where ‘t’ is in seconds. Determine the magnitude of particle velocity and acceleration when t = 4 sec. find the equation of path, y = f(x).
→ given : 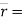 (8t2)i + (t3 + 5)j position vector
(8t2)i + (t3 + 5)j position vector
x = 8t2& y = t3 + 5
differentiating w.r.t. t
vx = 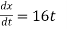 & vy =
& vy = 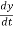 = 3t2
= 3t2
again differentiating w.r.t. t
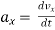 = 16t &
= 16t &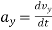 = 6t
= 6t
Now, at t = 4 sec
Vx = 16t = 16 × 4 = 64 m/sec
Vy = 3t2 = 3 × 42 = 48 m/sec
Magnitude of velocity
v = 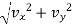
v = 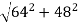
v = 80 m/sec
 = 16 m/s2
= 16 m/s2
 = 6t = 6 × 4 = 24 m/s2
= 6t = 6 × 4 = 24 m/s2
Magnitude of acceleration
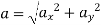
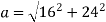
 28.84 m/s2
28.84 m/s2
Now as,
X = 8t2
t2 = x/8
t = 
but y = t3 + 5
put the value of t in this equation
y = [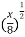 ]3 + 5
]3 + 5
y = 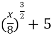 ---------path equation
---------path equation
Que 3. The y co-ordinate of the particle is given by y=4t3 – 3t. If ax = 12t m/s2& vx = 8 m/s at t = 0. Calculate the magnitude of velocity & acceleration of particle at time t = 2 seconds.
→ given : at t = 0, ax = 12t & vx = 8 m/s
at t = 2, v = ? a = ?
y=4t3 – 3t ------given
differentiating w.r.t. time ‘t’
 12t2 – 3
12t2 – 3
Vy = 12t2 – 3 ----------(1)
Differentiating again
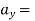 24t ----------(2)
24t ----------(2)
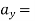 12t ----------(3) given
12t ----------(3) given
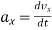 = 12t
= 12t
dvx= 12t dt
taking integration
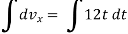
Vx = 12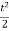 + c1
+ c1
Vx = 6t2 + c1
Now using the given condition
t = 0, vx = 8 m/s
8 = 6 × 0 + c1
c1 = 8
vx = 6t2 + 8 ---------(4)
at time t = 2 sec
vx = 6t2 + 8
= 6 × 22 + 8
Vx = 32 m/s
Vy = 12t2 – 3
= 12 × 22 – 3
Vy = 45 m/s
ax = 12t
= 12 × 2
ax = 24 m/s2
ay = 24t = 24 × 2 = 48 m/s2
magnitude of velocity at t = 2,
v = 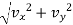
= 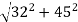
V = 55.21 m/s2
Magnitude of acceleration at t=2
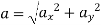
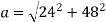
 53.66 m/s2
53.66 m/s2
Que 4. A particle is moving along a curve y = x -  . If vx = 4 m/s and is constant. Determine the magnitude of velocity & acceleration when x = 30 m.
. If vx = 4 m/s and is constant. Determine the magnitude of velocity & acceleration when x = 30 m.
→ given vx = 4 m/s (constant)
y = x - 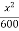
given equation of curve is
y = 
differentiating this w.r.t. ‘t’
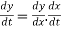 -------- by chain rule
-------- by chain rule
Vy = 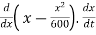
= (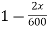 ).vx
).vx
= (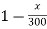 ).vx
).vx
Vy = vx (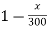 ) -------(1)
) -------(1)
Again differentiating w.r.t. ‘t’
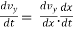 ---------using chain rule
---------using chain rule
ay = 
= [vx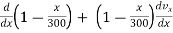 ]
]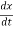
ay = [vx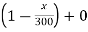 ]vx
]vx
= 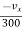 . vx
. vx
ay =  ------(2)
------(2)
now at x = 30 m
vx = 4 m/s
vy = vx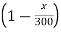
vy = 4
vy = 3.6 m/s
now as
vx = constant
ax = 0 &
ay = 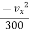
ay = 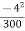
ay = - 0.053 m/s2
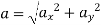
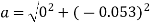
 0.053 m/s2 ↓
0.053 m/s2 ↓
As ax = 0 a must be downward because ay is negative.
Numerical on Tangential & Normal Components (Eqn of Motion in path coordinates)
*A car is travelling on a cured portion of Highway of radius 350 m at a speed of 72 kmph. The brakes are suddenly applied, Causing the speed to decrease at a constant rate of 1.25 mph. Determine the magnitude of total ace of car (a) immediately after the brakes have been applied (b) 4 sec. later.

Given:  = 350 m
= 350 m
V 72 = kmph = 20 m/s
 T = Tangenhal accn represents change in speed.
T = Tangenhal accn represents change in speed.
:.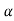 t = -1025 m/2
t = -1025 m/2
At the instant when brakes are applied;
Speed of car = v = 20/s
:. an = V2/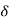 = 202/350 = 10143 m/
= 202/350 = 10143 m/ 2
2
:. Magnitude of Total Acc/n is
A=  aT2+aN2 =
aT2+aN2 =  (1.25)2 + 1.1432 = 1.69
(1.25)2 + 1.1432 = 1.69
:.a = 1069 m/s2
After t= 4 sec,
Velocity of car will be decreased due to application of brake.
:. Final velocity after 4 sec = V
Initial velocity before 4 sec = u = 20 m/sec.
:. Using V = u+aT t = 20+(-1025)*4 = 20-5
:. V 15 m/sec.
:. awn= v2/ = 152/350 = 0.64m/s2
= 152/350 = 0.64m/s2
:. Magnitude of Total Ac(1.252)c/n is,
a= 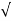 aT2+ aN2 =
aT2+ aN2 = 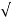 (1.25)2+ 0.642 =a= 1.4m/s2
(1.25)2+ 0.642 =a= 1.4m/s2
*A rocket a path such that its accn is given by a = (4i +tj) m/s2 at x =0 it start from rest. t= (4i +tj) m/s2 at x= 0 it start from rest.t= 20 sec., determine, 1) speed of rocket,2) Radius of curvature of its path  ) Magnitude of Tagential & Normal components of acceleration.
) Magnitude of Tagential & Normal components of acceleration.
a = ai + tj Radius of curvature ( :. a = dv/dt = 4i + tj ( Integrating Both sides, δ dv =[ (4i + tj)dt [ :. V = [(4 dt )I + [ ( tdt ) j V = ( 4t)I + ( t2/2) j + c1. :. | Now, at t=0, v=0, Normal Acc/n, :. C1= 0 Now At t= 20 sec. aN = V/ a = 4i + tj :. aN = 3.71m/s2 a = 4i + 20 j :. Ax = 4 m/s2 & ay = 20m/s2 Tangential Acc/n Also, V = (4t) I + (t2/2) j aT = = (4*20) I + (202/2) j :. V = 80 I + 200 j :.V 80 m/s & Vy = 200 m/sec. aT 20.04 m/s2 :. Magnitude of velocity V = Magnitude of Acceleration. a = :. a= 20.39 m/s2
|
Determine the distance travelled & time taken by a car starting from rest, moving on a circular curve having a radius of 275m, and accelerates at constant rate of tangential accln of m\s2& total accln of 1.4 m\s2.
Given : 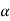
: 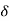 = 275m
= 275m
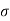 = 1 m\s2 - constant
= 1 m\s2 - constant
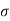 = 1.4 m/s2
= 1.4 m/s2
u = 0 m/sec – car starting from Rest.
Normal component of Acc/n,
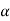 N =
N = 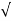 a2 - a2T
a2 - a2T
= 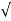 1.42- a2
1.42- a2
AN = 0.979 m/s2
But aN = V2/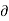 :. V2 = aN.
:. V2 = aN.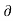
:. V2 = 0.979 * 275
:. V = 16.41 M/s
As AT = constant, Motion is UAM. Using eqn of motion,
V2 = u2 + 2aT S.
:. 16.412 = 0+ 2* a* S.
S = 134. 64 m. – distance travelled.
Using V = u+ 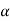 T t
T t
:. 16.41 = 0 + 1*t
:. T = 16.41 sec - time taken.
- A particle travels a curved path of radius 600 m with a speed of 108 kmph & a tangential acceleration of 4 m/s2 . Determine the total Acceleration of the particle.
Given 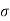 = 600 =
= 600 =
V = 108 kmph = 108 * 5/18 = 30 m/sec.
 T = 4 m/ sec2.
T = 4 m/ sec2.
:. We know that
Normal component of Acc/n is given by
 N = V2/
N = V2/ 
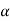 N = 302/600 = 900/600 = 1.5 m/ s2
N = 302/600 = 900/600 = 1.5 m/ s2
magnitude of total acc/n of a particle is,
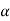 =
= 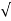 a2 T +aN2
a2 T +aN2
 =
=  42 + 1.52
42 + 1.52
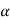 = 4.27 m/s2
= 4.27 m/s2
Magnitude of total acc/n of a particle is,
 =
= 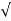 a2T + aN 2
a2T + aN 2
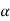 =
= 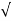 42 +1.52
42 +1.52
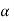 = 4.27 m/s2
= 4.27 m/s2
- A particle along a curve y = 1+ ws X with constant speed of 4m/s. find Tangential & Normal component of velocity & Acc/n,
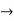 V = 4m/s - constant
V = 4m/s - constant
:.  T = 0
T = 0
Tangential component of velocity = VT = V = 4m/s
Normal component of velocity = VN = 0.
:. Y = 1+ cosx putting all values in above eq/n of ‘ ’
’
:. Dy/dx = -sin x |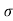 | = [ 1+ (-sin x )2] 3/2/-cosx = (1+ sin2) 3/2/ cosx
| = [ 1+ (-sin x )2] 3/2/-cosx = (1+ sin2) 3/2/ cosx
:. d2y/ dx2 = -cosx :. 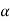 N = V2/
N = V2/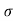 = 42/(1+sin2x)3/2/cosx
= 42/(1+sin2x)3/2/cosx
|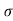 |= [1+(dy/dx)2]3/2/d2y/2 :. :.
|= [1+(dy/dx)2]3/2/d2y/2 :. :.  N = 16cosx/(1+ sin2X) 3/2
N = 16cosx/(1+ sin2X) 3/2
Numerical on Radial & Transverse Co- ordinates. (Eqn of motion in poplar Co- ordinates
- A particle moves in a circular path of radius 0.4m. Calculate magnitude of Acc/n of the particle if its speed is 0.6 m/sec but it is increasing at a rate of 1.2/sec each second.
 Given :
Given : 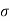 = 0.4 m
= 0.4 m
V = 0.6 m/s
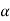 =
=  T = 1.2 m/s2
T = 1.2 m/s2
In case of circular motion 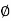 & tangential direction
& tangential direction
Coincides :.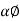 =
=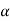 T = 1.2 m/s2
T = 1.2 m/s2
Also, positive r dirn is in negative Normal dirn.
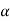 r = -aN ,
r = -aN ,
:. :. Total Acc/n = :. :. A particle moves an a curved path defined by polar co- ordinates. At certain instant,
:. 16 =( 2r * 0.5 + 5*4) :. r = -4 mm/s V = ear+ (r :. V = -4 eR + 2.5 e :. V =
|
A particle position is described by co- ordination r= 2sin 2 meterits &
meterits &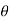 = (4t) rad, where t is in second. Determine the radial & transverse component of its velocity & Acc/n at t = 1 sec.
= (4t) rad, where t is in second. Determine the radial & transverse component of its velocity & Acc/n at t = 1 sec.
r = 2 sin2 Differentiating w.r.t t, dr/dt = dr/d :. r = 2*2 cos2 = 4 cos 2 r = 4 Again differnating w.r.t t Dr/dt = dt/d r = 4 = 4( .. r = - 8 ( Nt t=1, :. t= 1, :. r=2 sin 2 :. r = 4 :. r = 4 rad/s
Vr = r = - 2.33 m/s. :. Vr = -2.33 m/s V V
= - 18.64 m/s2 :.
|
*Projectile Motion *
* When a particle is freely thrown in the air along any direction other than vertical it follows it follows the parabolic path .The motion of a particle along this parabolic path is called as projectile motion.
* i.e. when we project the particle in the space, its motion is a combination of horizontal & vertical motion. This motion is called as projectile Motion.
* Wind Resistance, curvature & rotation of the earth affects the actual path.
But these parameters are neglected.
- The path Traced by projectile is called as Trajectory.”
- The motion of projectile in Horizontal direction is uniform motion.
- Ax = Horizontal component of acceleration = 0
- The acceleration in vertical direction is affected by gravity. Thus motion in y direction is considered as “Motion under gravity.”
:. 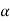 y = -
y = -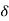
* Basic Terms involved in the projectile Motion *
1) Time of flight :- (t)
- The time by the projectile to move from point of projection to the point of target is called as “Time of flight.”
- It is the total time during which projectile remains in space.
2) “Horizontal Range” :- (R)
It is Horizontal distance from point of projection the point of target. OR
It is Horizontal distance bet/n point of projection & point of landing.
3) Maximum Height :- (H) or (Hmax) .
It is the vertical distance bet/n the point of projection and the point © where the vertical component of velocity is zero.
4) Angle of projection :( 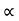 )
)
- It is the angle made by velocity with the Horizontal.
- If velocity is directed up the horizontal, then it is called as angle of elevation.
-If the velocity is directed down the Horizontal, then it is called as angle of depression.
5) Trajectory:-
It is the path traced by a projectile during its motion. It is parabolic in nature.
*projectile on Horizontal plane*
Consider a projectile projected from point A with
u= initial velocity of projection &
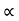 angle of projection.
angle of projection.
Let t = total time of flight.
Thus projectile will land at point b after time ‘t’ Both point A& B are Qn H.P
Diagram
|
As the air resistance is neglected, the motion in X-direction is uniform motion & y dirn motion is Motion under Gravity”.
a) Time of flight (t)
t 2 u sin /
/
b) Horizontal Range (R)
R = u2. Sin2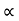 /
/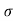
c) Maximum Range (R max)
For maximum Range angle of projection must be 45
R max = u2/
d) Maximum Height
H = u2. Sin2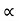 /2
/2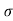
*Derivation of path Equation*
[ Eqn of Trajectory]
Vx= u cos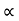 = constant.
= constant.
Vy = u sin 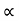
|
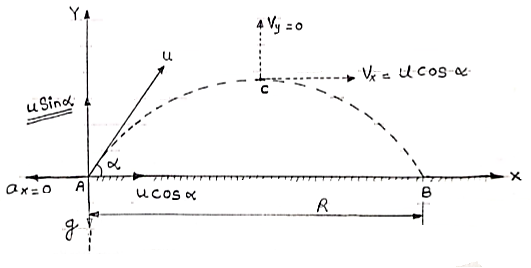
Consider a particle projected from A with initial velocity ‘u’ & angle of projection ‘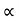 ’.
’.
Let after time ‘t’ , the particle has reached at point p (x,y).
Consider the motion of projectile in X dirn ( VM) :- [ A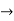 p]
p]
S= velocity * time
X = u cos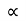 . t1
. t1
:. t1 = X/ u cos  . t1
. t1
:. t1 = X/ u cos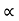 . --------- (1)
. --------- (1)
Consider the motion of projectile in y dir/n ( m. U.G) [ A 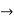 p]
p]
:. Sy= uyt1- ½  t2
t2
Y = u sin  .t1 – 1/2
.t1 – 1/2 t12
t12
From eq/n (1), put the value of time t1
:. y = u sin 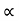 .(x/ucos
.(x/ucos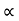 .) – ½
.) – ½  (x/ u-cos
(x/ u-cos .)2
.)2
:. y = X. tan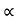 - gx2/u2 cos2
- gx2/u2 cos2 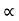
:. y X. tan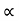 - gX2/2u2 cos2
- gX2/2u2 cos2 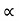
Eqn of Trajectory.
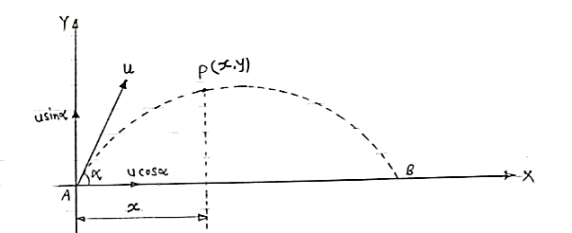
*projectile on Inclined plane*
|
Let projectile is projected from point A.
let
 angle projection with (inclined) plane.
angle projection with (inclined) plane.
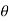 = Angle of inclined plane with Horizontal.
= Angle of inclined plane with Horizontal.
Now let us select X axis along the inclined plane and y –axis perpendicular to the inclined plane.
:. X component of velocity = u cos
:. Y - ----- -------------------- u sin 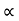
Similarly for gravitation Acc/n ‘g’
X component = g sin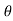
y component = g cos 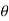
a) Time of flight (t) b) Range along the plane (R)
t= 2u. sin 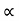 /g cos
/g cos  R= 2 u2 sin
R= 2 u2 sin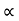 / g cos2
/ g cos2 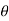 . Cos (
. Cos (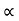 +
+ )
)
c) Maximum Range (Rmax) d) Max. Height (lar to plane)
Rmax = u2/g (1+sin ) H = u2 sin2
) H = u2 sin2 / 2g. cos
/ 2g. cos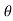
*Special cases of projectile*
*projectile projected with Horizontal velocity:-*
X motion
Consider motion A  B
B
(V.M)
X = u*t
|
Consider Motion (y- motion)
From A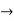 B (M.V.G)
B (M.V.G)
S = ut + ½ gt2
h= 0 + ½gt2
:. t=  2h/g
2h/g
:. Horizontal distance, = X = u 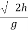
Y = x tanx - gx2/u2 cos 2 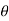 -eqn of trnjectory
-eqn of trnjectory
But 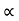 = 0 At point A.
= 0 At point A.
:. –h = -y = 0 - gx2/2u2
:. h = gx2 / 2u2
*for given values of u, two angle gives us the same Range.
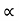 1 =
1 = 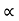
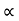 2 = π/2 -
2 = π/2 -
Numerical on projectile Motion. (Projectile on Horizontal plane)
*A projectile is fired with a velocity of 60 m/s on Horizontal plane. Find its time of flight in the following 3 cases.
a) is Range is 4 times the max . Height
b) Its max height is 4 times Horizontal range.
c) Its max. Height & Horizontal range are equal.
 u = 60m/s
u = 60m/s
a) When R = 4 H
u2 sin 2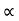 /g=4 [ 4 2.sin2
/g=4 [ 4 2.sin2 /2g]
/2g]
:. u2/g 2sin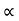 cos
cos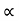 = 242/g sin2
= 242/g sin2
:. Cos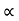 = sin
= sin 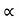
:. Cos  - sin
- sin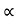 =o
=o
:. = 45
= 45
Time of flight t= 2usin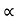 /g = 2* 60* sin 45/9081 = 8.65 sec.
/g = 2* 60* sin 45/9081 = 8.65 sec.
b) When H = 4R
:. u2sin2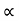 /2g = 4[ 42 sin 2
/2g = 4[ 42 sin 2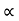 /g]
/g]
:. Sin2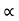 = 8 sin 2
= 8 sin 2
:. sin =(2*8) cos
=(2*8) cos
:. sin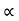 = 16 cos
= 16 cos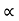
:. tan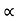 = 16 &
= 16 &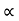 = 86.42
= 86.42
t= 2usin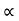 /g = 2*60*sin86.42?9.81 = 12.21 sec
/g = 2*60*sin86.42?9.81 = 12.21 sec
c) When H = R
u2sin2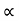 /2g = u2 sin2
/2g = u2 sin2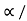 g t= 2usin
g t= 2usin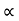 /g
/g
:. Sin2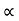 /2 = sin2
/2 = sin2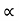 = 2*60*sin75.96?9.81
= 2*60*sin75.96?9.81
:.Sin2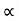 = 2*2 sin
= 2*2 sin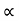 cos
cos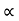
:. Sin 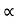 = 4 cos
= 4 cos t = 11.87 sec.
t = 11.87 sec.
:. tan =4 :.
=4 :. = 75.96
= 75.96
A projectile is aimed at an object Qn a H.p through the point of projection and tall 8 M 8 short when the angle of projection is 15 , while it overshoots the the object by 18 m when the angle of projection is 45
, while it overshoots the the object by 18 m when the angle of projection is 45 Determine the angle of projection to Hit the object exactly.
Determine the angle of projection to Hit the object exactly.
 let R = actual Range Required to hit the object.
let R = actual Range Required to hit the object.
 ax I -
ax I - 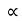 =15
=15
Range = R -8
:. u2* sin(2*15)/g = (R-8)
:. Multiply both sides by 2
:. 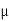 2/g = 2R-16----------(1)
2/g = 2R-16----------(1)
Cos (2) 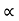 =45
=45
Range = R +18
u2 sin2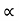 /g = R+18
/g = R+18
u2/g. sin 90 = R +18
:. 42/g = R =18------------ (2)
From (1) & (2) R +18 = 2 R- 16
:. 2R – R = 18+16 = 34.
:. 2R = 34m ---- Actual Range to hit the object
Actual Range
R (42/g) sin 2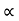
34 = (R +18) sin2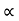
34 = (34+18) sin2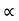
34 = 52 sin 2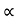
:. Sin 2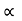 = 0.653
= 0.653
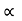 = 20.38
= 20.38 - Angle of projection to hit the object
- Angle of projection to hit the object
A shot is fired from the gun .After 2 sec. the velocity of shot is inclined at 30 up the horizontal After 1 more second. It attains max height. Determine the initial velocity and angle of projection.
up the horizontal After 1 more second. It attains max height. Determine the initial velocity and angle of projection.
Let, u = initial velocity 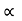 = angle of projection. Let, after. 2 second, the shot fired from gun reaches at point D Here Vo makes 30
= angle of projection. Let, after. 2 second, the shot fired from gun reaches at point D Here Vo makes 30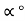 angle with Horizontal.
angle with Horizontal.
&
|
Let after one more second , shot attains max , Height at point C as shown in figure.
At point D, V0 makes 30 with Horizontal.
with Horizontal.
:. X component of velocity at ‘D’ = VD cos 30
But we know that velocity in X dirn is constant (U.m.) :. VD cos 30 = u cos :. 0.87 VD cos 30 = ucos Consider y-Motion from A to D. By substituting the value of VD in eqn (1) & (2) This is Motion under gravity 0.87 VD = u cos :. V = u +at : U cos :. VD sin 30 = usin :. 0.5 VD = usin :.0.5 VD = usin Now Consider y motion from D-c ,(M.V.G) Also, usin V = u +at = 0.5*19.62+ 19.62 0 = VD sin30 – g*tDC =u sin 0= 0.5 VD – 9.81 *1 from eqn (3) & (4) :. 0.5 VD = 9.81 usin :. VD = 19.62 m/s : tan :.
|
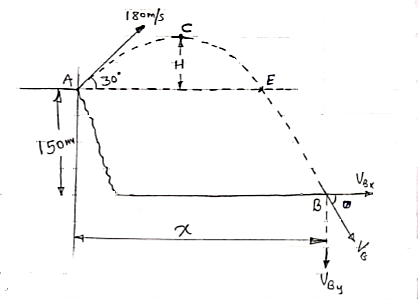
A projectile is fired from the edge of 150 m cliff an initial velocity of 180 m/s at 30 angle with Horizontal. Find 1) The Horizontal distance from the gun to the point where the projectile strikes the ground 2) The greatest elevation above the ground reached by projectile 3) striking velocity. Refer the given figure.
angle with Horizontal. Find 1) The Horizontal distance from the gun to the point where the projectile strikes the ground 2) The greatest elevation above the ground reached by projectile 3) striking velocity. Refer the given figure.
|
Let
X= Horizontal distance between A& B
A= point of projection
B= point of striking. We can see from the fig that A& B are not on same level. TAB = time Req = tAB Consider the Horizontal motion from A to B (U.M) :. Distance = velocity * time X = 180 cos 30 * tAB X= 155.88 tAB ------ (1) Consider vertical motion from A to C, H+ 150+ ½*9.81* t2CB : V = u + at 412.84+ 150 = 4.905 +tCB Vcy = 180sin30- g*tAC : t2CB = 562.84/4.905 :0 = 90 – 9.81 tAC :. t2CB = 114.748 :tAC = 90/9.81 :. tCB = 10.71 sec :tAC = 9.17 sec. tAB = 9.17 + 10.71 = 19.88 sec H = u2sinsin2 X = 3098.9 m H = 412.84 m. :. Now using. Eqn of motion S = ut + ½ gt2
Horizontal distance from the to the point of striking is X = 3098.9 m Time req. from A to B = tAB = 19.88 sec. Greatest Height Reached by projectile above the ground is Hmax H + 150 = 412.84+150 Hmax = 562.84 m Now, Consider that VB = striking velocity. & Ø = angle made by striking velocity with Horizontal. As shown. Let VBX = X component of VB. VBy = y component of VB. But we know that,in X dirn, motion is uniform. Thus VBX = u cos To find VBy consider the motion from C to B. :. V = u + gt VBy = Vcy + g * tCB VBy = 0 + 9.81 * 10.71 VBy = 105.06 m/sec :. VB = VB = 187.9 m/sec Tanø = VBy/ VBX = 105.06/155.88 :. Ø = 33.97
|
|
Reference Books:
1. Engineering Mechanics by S. P. Timoshenko and D. H. Young, McGraw- Hill publication
2. Engineering Mechanics by J. L. Meriam and Craige, John Willey
3. Engineering Mechanics by F L Singer, Harper and Rowe publication
4. Engineering Mechanics by A. P. Boresi and R. J. Schmidt, Brooks/Cole Publication