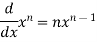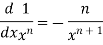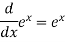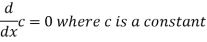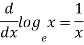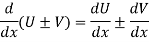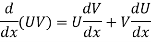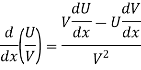Unit-3
Derivatives and applications of derivatives
Limits-
The function f(x,y) is said to tend to limit ‘l’ , as x →a and y→bIff the limit is dependent on point (x,y) as x →a and y→b
We can write this as,
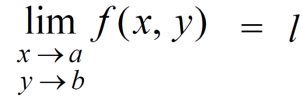
Example-1: evaluate the 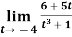
Sol. We can simply find the solution as follows,

Example-2: evaluate 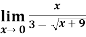
Sol.
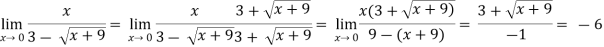
Example-3: evaluate 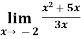
Sol.
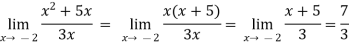
Increment-
Increment of a variable means the difference of initial value from the final value
Increment = final value – initial value
Let x change its value from 2 to 8, increment of x = 8 – 2 = 6
Note- increment can be negative or positive.
Here we will denote the increment of x by 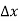
If in y = f(x), the independent variable x changes to 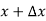 then the increment of x =
then the increment of x = 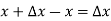
So y = f(x) changes to y = f(x + 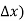
Increment of y = f(x + 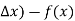
Then the increment ratio-
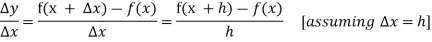
If the ratio 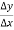 tends to a limit, as
tends to a limit, as 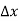 ® 0 from either side, then this limit is known as the derivative of
® 0 from either side, then this limit is known as the derivative of
y [ = f(x)] with respect to x.
A function y = f(x) is said to be derivable at x if
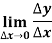
Or

Or

Derivative of y = f(x) with respect to x is denoted by dy/dx or 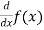
Some useful derivatives-
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
Example: Find dy/dx of the following functions-
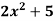
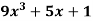
Sol.
Let y = 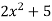
Then-
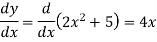
and
Let y = 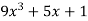
Then-
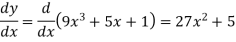
Example: Differentiate 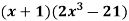 with respect to x.
with respect to x.
Sol.
Let 
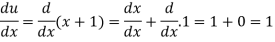

Now
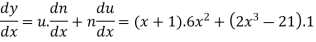
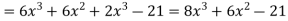
Example: if 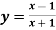 then find dy/dx.
then find dy/dx.
Sol.
Suppose y = u/v where u = x - 1 and v = x + 1
Then
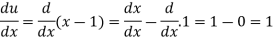
And
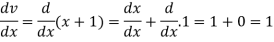
So that-
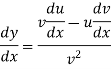
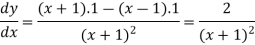
Derivative of function of a function-
If y = f(z), z = 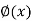 then y = f{
then y = f{
Now if y = f(z) and z = z = 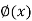 then-
then-
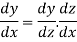
Derivative of logarithmic function and exponential function-
If y = log x then its derivative will be-

If y = 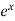 then its derivative-
then its derivative-
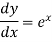
Note- derivative of a constant is always zero.
Example: if y = 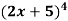 then find dy/dx.
then find dy/dx.
Sol.
Suppose z = 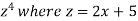
Now-
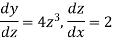
So that-
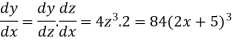
Example: if y = 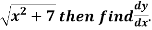
Sol.
Suppose y = 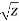 where z =
where z = 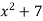
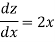
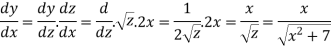
Example: If y = log loglog then find dy/dx.
then find dy/dx.
Sol.
Suppose y = log u where u = log v and v = log 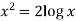
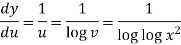
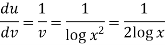
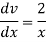
So that-
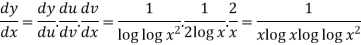
Example: if y = 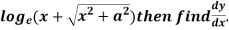
Sol.
Let y = log u where u = 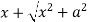
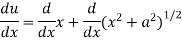

Now
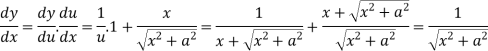
Example: find the derivative of the function f(x) = 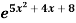 .
.
Sol.
Let y = f(x) then
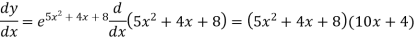
Example: Find the derivative of 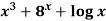
Sol.
Let y = 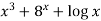 then
then

Implicit function and inverse function-
Functions are also classified into two categories- implicit and explicit.
Explicit function- the function where one variable can be expressed as a function f another variable only as y = f(x) otherwise the function is taken as implicit function
Or we can define the implicit function as follows-
Implicit function is one where the independent input and its dependentoutput are not given directly as is done with y = f(x)
For example- y = 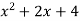 is an explicit function and y =
is an explicit function and y = 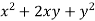 is an implicit function.
is an implicit function.
Partial derivative
First order partial differentiation-
Let f(x, y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as 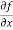 and defined as follows:
and defined as follows:
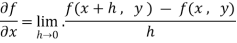
Now the partial derivative of f with respect to f can be written as  and defined as follows:
and defined as follows:
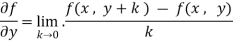
Note: a. while calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating, as constant.
b. we apply all differentiation rules.
Higher order partial differentiation-
Let f(x , y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives.
These are second order four partial derivatives:
(a) 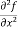 =
= 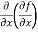
(b) 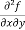 =
= 
(c)  =
= 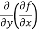
(d) 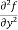 =
= 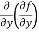
b and c are known as mixed partial derivatives.
Similarly we can find the other higher order derivatives.
Example-1: Calculate  and
and 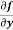 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate 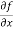 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
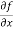 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 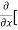 3x³] -
3x³] -  5y²] +
5y²] +  [2xy] -
[2xy] -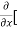 8x] +
8x] +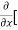 4y] -
4y] - 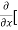 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
 =
= 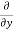 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 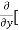 3x³] -
3x³] - 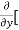 5y²] +
5y²] + 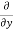 [2xy] -
[2xy] -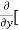 8x] +
8x] +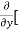 4y] -
4y] - 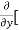 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Example-2: Calculate 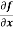 and
and  for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Sol. To calculate 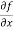 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)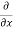 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8) (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Example-6: if 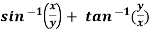 , then show that-
, then show that- 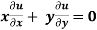
Sol. Here we have,
u = 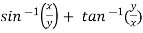 …………………..(1)
…………………..(1)
now partially differentiate eq.(1) w.r to x and y , we get
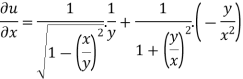
= 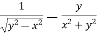
Or
 ………………..(2)
………………..(2)
And now,
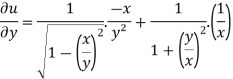
= 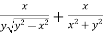
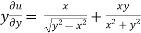 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
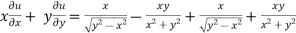 = 0
= 0
Hence proved.
Key takeaways-
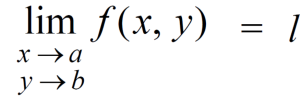
2. Increment of a variable means the difference of initial value from the final value
Increment = final value – initial value
3. the increment ratio-
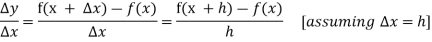
4. A function y = f(x) is said to be derivable at x if

5. Derivative of y = f(x) with respect to x is denoted by dy/dx or 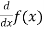
6. 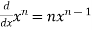
7. 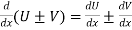
8. 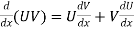
9. 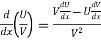
10. Implicit function is one where the independent input and its dependent output are not given directly as is done with y = f(x)
11. the partial derivative of f with respect to f can be written as 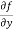 and defined as follows:
and defined as follows:
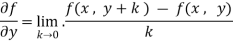
12. while calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating, as constant
13. We apply all differentiation rules.
The derivative of dy/dx is known as the second order derivative of y.
It is denoted by 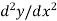
Example: if y = log x/ x a then find 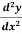
Sol. First we will find the first derivative-
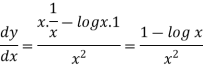
Now
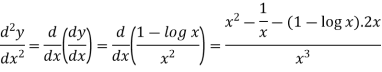
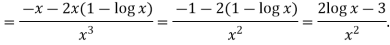
Example: if y = 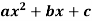 then find
then find 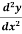
Sol.
Here
y = 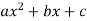
diff. W.r.t. x, we get-
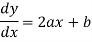
Now
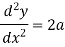
Example: if y = 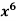 then find
then find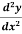
Sol.
Here
y = 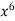
then
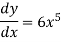
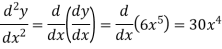
A function f(x) is said to be maximum at x = a if f(a) is greater than every other value of f(x) in the immediate neighbourhood of x = a (i.e., f(x) ceases to increase but begins to increase at x = a. Similarly the minimum
value of f(x) will be that value at x = b which is less than other values in the immediate neighbourhood of x= b.
Maxima and minima of function of two variables-
As we know that the value of a function at maximum
Point is called maximum value of a function. Similarly the value of a function at minimum point is called minimum value of a function.
The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complement of each other.
Maxima and Minima of a function of one variables
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point 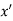 if and only if
if and only if 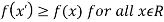
Minima is a minimum point  if and only if
if and only if 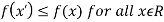
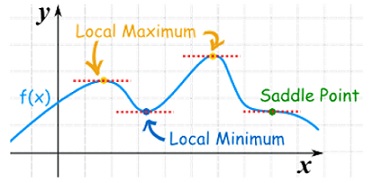


Maxima and Minima of a function of two independent variables
Let 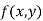 be a defined function of two independent variables.
be a defined function of two independent variables.
Then the point  is said to be a maximum point of
is said to be a maximum point of 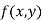 if
if
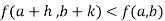
Or 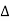 =
= 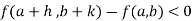
For all positive and negative values of h and k.
Similarly the point 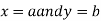 is said to be a minimum point of
is said to be a minimum point of  if
if
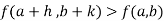
Or 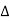 =
= 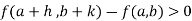
For all positive and negative values of h and k.
Saddle point: Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
Note-
Criteria for maximum and minimum-
For a function y = f(x) to attain a maximum point at x = a,
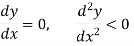
For minimum point-
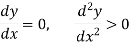
Conditions for max. and min-
Necessary Condition- If a function f(x) is maximum or minimum at a point x = b and if f’(b) exists then f’ (b) = 0.
Sufficient Condition-If b is a point in an interval where f(x) is defined and if f ‘(b) = 0 and f’’(b) 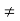 0, then f(b) is maximum if f’’(b) <0 and is minimum if f’’(b) > 0. (The proof is not shown at present).
0, then f(b) is maximum if f’’(b) <0 and is minimum if f’’(b) > 0. (The proof is not shown at present).
Working Rule:
First derivative method
To find the maximum or minimum point of a curve y = f(x).
Find f ‘(x) and equate it to zero. From the equation f ‘(x) = 0, find the value of x, say a and b.
Here the number of roots of f ‘(x) = 0 will be equal to the number of degree of f ‘(x) = 0.
Then find f ‘(a – h) and f ‘(a + h), then note the change of sign if any (here h is very small).
If the change is from positive to negative, f(x) will be maximum at x = a. If again the change of sign is from negative to positive, f(x) will be maximum at x = a.
Similarly for x = b.
Second derivative method-
First we find the first derivative of y = f(x) i.edy/dx and make it zero.
From the equation 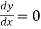 find the value of x say a and b.
find the value of x say a and b.
The again we find the second derivative of y or 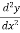 .
.
Put x = a in 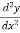 , if
, if 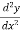 at x = a is negative then the function is maximum at x = a and maximum value will be f(a).
at x = a is negative then the function is maximum at x = a and maximum value will be f(a).
If the value of 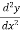 at x = a is positive, then the function is minimum and the minimum value will be f(a)
at x = a is positive, then the function is minimum and the minimum value will be f(a)
Similarly we take for x = b.
Example: Examine for maximum and minimum for the function f(x) = 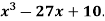
Sol.
Here the first derivative is-

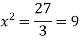
So that, we get-
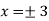
Now we will get to know that the function is maximum or minimum at these values of x.
For x = 3
Let us assign to x, the values of 3 – h and 3 + h (here h is very small) and put these values at f(x).
Then-
 which is negative for h is very small
which is negative for h is very small
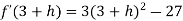 which is positive.
which is positive.
Thus f’(x) changes sign from negative to positive as it passes through x = 3.
So that f(x) is minimum at x = 3 and the minimum value is-
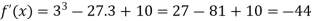
And f(x) is maximum at x = -3.
Example: Find out the value of x for which the function f(x) = 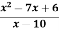 is minimum of maximum.
is minimum of maximum.
Sol.
Let y = f(x) = 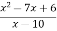
Then the first derivative will be-
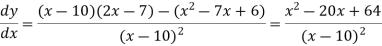
Putting 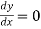 , we get-
, we get-

By using middle term splitting-
We get-
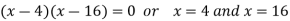
Now we will find the second derivative-
We get-
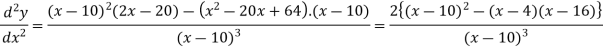
Here
At x = 4, 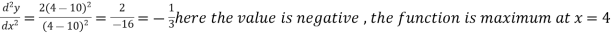
At x = 16, 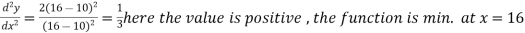
Key takeaways-
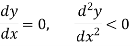
For minimum point-
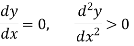
3. Necessary Condition- If a function f(x) is maximum or minimum at a point x = b and if f’(b) exists then f’ (b) = 0.
Sufficient Condition- If b is a point in an interval where f(x) is defined and if f ‘(b) = 0 and f’’(b)  0, then f(b) is maximum if f’’(b) <0 and is minimum if f’’(b) > 0. (The proof is not shown at present).
0, then f(b) is maximum if f’’(b) <0 and is minimum if f’’(b) > 0. (The proof is not shown at present).
Some important definitions-
Fixed cost- The cost remains constant for all levels of output.
For example, cost of machinery orrent of factory building
Total Cost- Total cost is the sum of two components, viz., fixed costand variable cost. Symbolically, TC= FC+ VC, where TC= total cost,
FC= fixed cost and VC= variable cost.
Variable Cost- The cost varies with level of output. For example, costof raw materials forms a part of variable cost
Average Cost- which is defined as per unit cost of production andwritten as
AC = TC/q
where q is units of output
Marginal Cost- which is the rate of change in total cost when q units are produced and written as-
MC = d TC/ dq
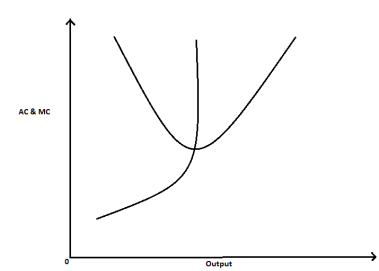
Graph of the relationship between the average cost and marginal cost-
Note-
Example: The total cost function of the firm is given by-
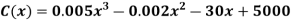
Where x is the output.
Find out-
Sol.
Here we have-
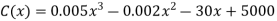
Now
FC = 5000
2. Average cost = TC/x = 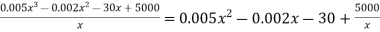
3. MC = d TC / dx 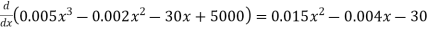
4. Marginal average cost = d AC / dx = 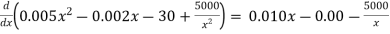
Example: if TC = 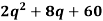 then calculate AC and MC at q = 3.
then calculate AC and MC at q = 3.
Sol. here we have-
TC = 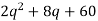
Therefore-
AC = TC/q


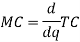
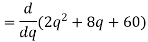

When q = 3, MC = 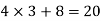
Total revenue-
Revenue function shows the relation between price of the commodity andoutput sold. If X units of an output are sold at a price p per unit, then the totalrevenue R(x) is given by-
R(x) = x· p
Marginal revenue-
Marginal Revenue (MR)is the change in total revenue resulting from anadditional unit of output sold. Thus,
The marginal revenue represents the change in TR for each additional unit of sale
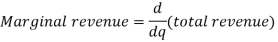
Note:For profit maximisation, MR = MC.
Example: A manufacturer can sell x items per month at a price p = 300 – 2x rupees. Produced items cost the manufacturer y rupees y = 2x + 1000. How much profit will yield maximum profits
Sol.
Profit (P) = Sale – total cost = x. p – y
= x (300 – 2x) – (2x + 1000) = 298x – 2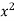 – 1000
– 1000
For maximum profit-

Again the second derivative is-

Hence the profit will be maximum for 74 items.
Example: The sum of two numbers is 12. Find the maximum value of their product.
Sol.
Let the two numbers be x and y, so that x + y = 12
Product (P) = xy = x (12 – x) = 12x –

For product maximum-

Again-
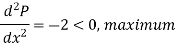
The required product = x (12 – x) = 6 (12 – 6) = 6.6 = 36
Revenue function-
The revenue function is the relationship between revenue and output.
Let us write the total revenue,
TR = p.q = p f(q)
where p is the price per unit of the good and q is the number of units of the commodity sold.
To see the nature of relationship between revenue and output, we need to check the price elasticity and demand,
Let the total revenue be-
TR = pq
If let the price changes to be p +  and the quantity changes to q +
and the quantity changes to q + 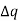 ,
,
The revenue becomes-
R = (p + 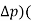 q +
q + 

Subtracting TR from R, we get-

For small values, we can neglect the last term and then we get-
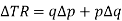
The rate of change of revenue per unit change in price is given as-
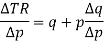
Note-
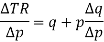
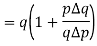
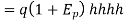
Here 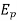 is price elasticity of demand.
is price elasticity of demand.
We know that the elasticity of demand is negative so that we can write it as-
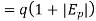
Elasticity and marginal revenue-
We know that the change in revenue is given by-
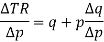
Or
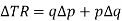
Divide by  both sides-
both sides-
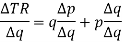
Or
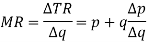
Or
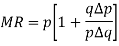
Note-
We can write it as-
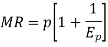
Note- if elasticity of demand is −1, then marginal revenue is zero.
Maximizing of total revenue-
If the demand function of a firm is given then we can find the corresponding level of output whose total revenue is maximum by using the concept of maxima and minima.
The total revenue is maximum when marginal revenue is zero.
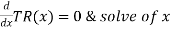
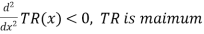
Example: A belt manufacturer produces high grade and low grade shoes in x units (hundred pairs) and y units (hundred pair) per day respectively.
Assume that the equipment is capable of producing the belts in the following relationship-
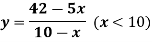
If the high grade belt are sold at a price twice the low grade belts.
Determine the pairs of both the belts he should produce to maximize his total revenue.
Sol. let the price of low grade belt be Rs. p per pair, then the price of high grade belts will be rs. 2 p per pair.
The total revenue will be-

Or
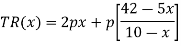
For maximizing TR(x), take its first derivative w.r.t. x, put it equal to zero and solve for x,
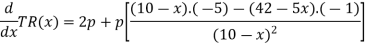
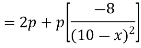
Now put it equals to zero and solving for x,
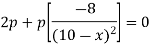
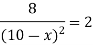
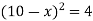
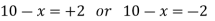
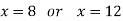
So that,
x = 8 [ x< 10, and x = 12 is not possible]
Now at x = 8,
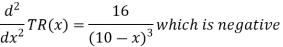
RT(x) is maximum at x = 8
Put this value in the function-
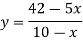
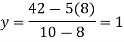
So that we can conclude that the total revenue is maximum when the manufacturer produces 800 pairs of high grade and 100 pairs of low grade.
Example: Find the total revenue and marginal revenue of the perfect competitive firm with current price of Rs. 10 per unit.
Sol.
Given, P= 10.
If q units are sold in the market then
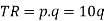
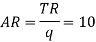
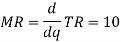
Therefore, P = AR = MR = 10 which is constant.
Under monopoly, price is determined by the firm and not given to it by the market. The total revenue will be maximum at a level of output where first order differentiation of total revenue is zero and second order derivative is less than zero
Example: For the following demand and cost functions-
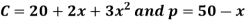
Find the output level and price at which the profit is maximized.
Sol.
Revenue (TR) = p.x = x (50-x) = 50x - 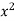
Profit ( = TR – TC
= TR – TC
= 50x - 
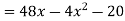
Diff w.r.t. x,
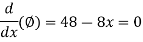
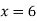
Now calculating second order derivative-
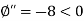
Hence, profit is maximum at x = 6, equilibrium price is-
P = 50 – x = 50 – 6 = 44
Hence, equilibrium output is 6 units and equilibrium price is 44.
Key takeaways-
AC = TC/q
where q is units of output
5. Marginal Cost- which is the rate of change in total cost when q units are produced and written as-
6. MC = d TC/ dq
7. Total revenue-
Revenue function shows the relation between price of the commodity and output sold. If X units of an output are sold at a price p per unit, then the total revenue R(x) is given by-
R(x) = x· p
8. 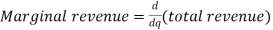
9. For profit maximisation, MR = MC
10. 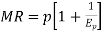
11. - if elasticity of demand is −1, then marginal revenue is zero.
The most common use of elasticity in economics and business studies is price elasticity of demand
This concept is based on law of demand. Law of demand means the quantitative relationship between price and quantity demanded and if the price is high, quantity demanded is low.
Price elasticity of demand is always negative because of negative relationship between price and quantity defined by law of demand.
If the price of a mineral water bottle were to increase, the quantity sold will be influenced
Suppose that in 2016, Bisleri increased the price of water bottle from Rs.
20.00 to Rs. 22.00. Due to such a change, the demand for water bottles dropped
from 500 units per day to 498 units per day.
Then the percent change in price P-
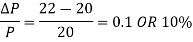
The percent change in demand Q-
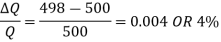
Thus the price elasticity of demand can be defined as-
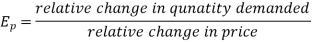
Or
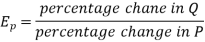
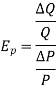
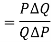
Now-
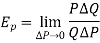
Which is-
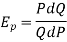
Example: If the demand function of a commodity is Q= 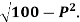 then determine the price elasticity of demand-
then determine the price elasticity of demand-
Sol.
Q = 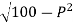
When, P= rs. 8 Q = 6 units
And when P = rs. 6 Q = 8 units.
So that,
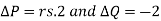
We know that-

2. At P = rs. 8, Q = 6 units,
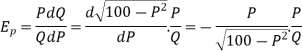

Example: The Namkeen industry decides to reduce the price of its product, from Rs.100 to Rs. 75. The company expects that the sales of Namkeen will increase from 10,000 units a month to 20,000 units a month. Calculate and comment on the price elasticity of demand.
Sol.
First, we need to calculate the percentage change in quantity demandedand percentage change in price. So,
% Change in Price = (Rs. 75-100)/(Rs.100) = -25%
% Change in Demand = (20,000-10,000)/(10,000) = 100%
Therefore, the Price Elasticity of Demand = 100%/-25% = -4.
This means the demand is relatively elastic
Key takeaways-
References-