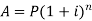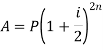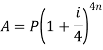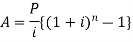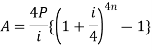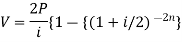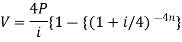Unit-1
Elementary Financial Mathematics
Calculation of interest is one of the most basic uses of mathematics in finance.
We can define the simple interest as- “the price has to be paid for the use of a certain amount of money or principal for certain period, is called interest”
Amount- This is the sum of the principal and the interest at any time.
The rate of interest is denoted by ‘i’.
Let the principal is 100 rs. And the interest is 8 then we can say that the rate of interest is 8 percent per annum or we can write it as r = 8%
Suppose ‘P’ is the principal and ‘n’ is the time for which the principal is given and ‘r’ be the rate of interest per annum
‘I’ be the amount of interest
And ‘i’ be the rate of interest per unit
Then-
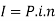
Here- i = r/100
We can calculate the amount as-
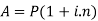
Example: Sushmita invested 5000rs. At the rate of 8 per cent per annum then what will be the value of the amount she invested in 5 years.
Sol.
Here P = 5000, i = 8/100 = 0.08, n = 5, now
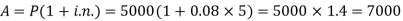
Hence the required amount is - 7000
Example: Find out the simple interest on 5600 rs. At 12 percent per annum from July 15 to September 26, 2020.
Sol.
Here we calculate the time-
Total days from july 15 to sept 26 = 73 days or 73/365 = 1/5 years
And P = 5600, i = 12/100 = 0.12
Simple interest = P.i.n. = 5600 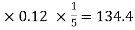
Hence the simple interest is – 134.40
Example: Harpreet invests 1200rs. At 10 percent per annum for some time and it becomes 1560 then find the principal when that will become 2232 at 8 percent p.a. in the same time.
Sol.
Here in first situation- P = 1200, A = 1560 and i = 0.10
So that,
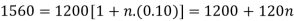
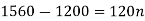
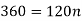
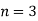
In second situation-
A = 2232, n = 3, i = 0.08
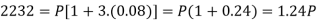
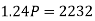
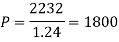
Compound interest-
In compound interest, the principal does not remain same but increases at the end of each interest period.
Let-
P- Principal
A - Amount
i = interest on re. 1 for a year
n = interest period
then the amount can be calculated as-
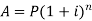
And
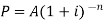
Note- By using algorithm the above formula can be written as-
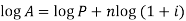
Note- if the compound interest is paid half-yearly, quarterly, monthly instead of a year the there will be different formulae as given in the table below-
Time | Amount |
Annually |
|
Half-yearly |
|
Quarterly |
|
Example: Aman invests 1000 rupees at 5 percent p.a for four years then find the compound interest on it.
Sol.
Here P = 1000, i = 0.05 and n = 4
Then we know that-
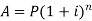

On taking log, we get-
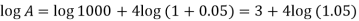
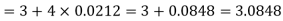
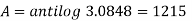
Compound interest will be-
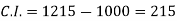
Which is the required answer.
Example:A sum of money invested at C.I. payable yearly amounts to 10, 816 rs. at the end of the second year and to 11,248.64 rs. at the end of the third year. Find the rate of interest and the sum.
Sol.
Here A1 = 10,816, n = 2, and A2 = 11,248.64, n = 3
We know that
A = P (1 + i)n we get,
10,816 = 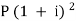 … (i)
… (i)
11,248.64 =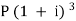 … (ii)
… (ii)
Here on dividing equation (2) by (1)-
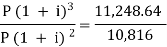
We get-
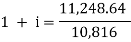

And
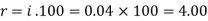
Hence the rate is 4 percent.
Now from first equation-
10,816 = 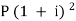
Or

Now-
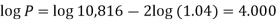
P = antilog 4.000 = 10,000
Therefore the require answer- 10,000
Nominal and effective rate of interest-
Nominal rate of interest is the rate of interest per annum which is compounded yearly, half yearly, quarterly, monthly, n times in a year or continuously.
Effective rate of interest is the rate of interest per annum compounded only once in a year.
There is a relationships between nominal and effective rate of interest under two different conditions-
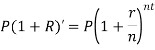
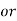
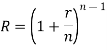
Where ‘r’ is nominal rate and ‘R’ is effective rate.
2. If compounding is continuous-
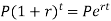
Or
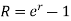
Relationship between two nominal rates-
If interest is compounded quarterly at 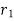 percent and the interest is compounded half yearly at
percent and the interest is compounded half yearly at 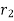 percent, then the relationship between the two is-
percent, then the relationship between the two is-
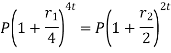

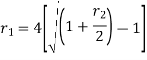
Example: Ronak deposited Rs. 10,000 in a bank for 3 years. Bank gives two offers either 10 percent compounded quarterly or 8% compounded continuously, then which offer is preferable for Ronak?
Sol.
Balance after three years under first offer-
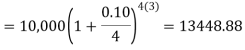
Balance after 3 years under second offer-
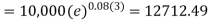
So that we can conclude that the first offer is preferable for Ronak
Key takeaways-
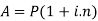
3. Compound interest- 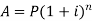
4. Nominal rate- Nominal rate of interest is the rate of interest per annum which is compounded yearly, half yearly, quarterly, monthly, n times in a year or continuously.
5. Effective rate- Effective rate of interest is the rate of interest per annum compounded only once in a year.
6. 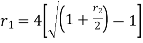
Annuity-
An annuity is a fixed sum paid at regular intervals under certain conditions.
The length of time during which the annuity is paid can either be until the death of the recipient or for a guaranteed minimum term of years, irrespective of whether the annuitant is alive or not.
Amount of an annuity:
Amount of an annuity is the total of all the installments left unpaid together with the compound interest of each payment for the period it remains unpaid.
The formulas to find the amount of annuity are given below-
| When annuity is payable annually and interest is also compounded annually |
| annuity is payable half-yearly and interest is also compounded half-yearly |
| annuity is payable quarterly and interest is also compounded quarterly |
Present value of an annuity-
Present value of an annuity is the sum of the present values of all payments (or installments) made at successive annuity periods
The formulas to calculate present value ‘V’ of an annuity P are given below-
| When V of an annuity P payable annually |
| When V of an annuity P payable half-yearly |
| When V of an annuity P payable quarterly |
Example:Sundar decides to deposit20,000rs. at the end of each year in a bank which pays 10% p.a. compound interest.
If the installments are allowed to accumulate, what will be the total accumulation at the end of 9 years?
Sol.
SupposeA rs. be the total accumulation at the end of 9 years. Then we get-
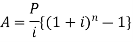
Here P = 20,000 rs., i = 10/100 = 0.1 and n = 9
Then
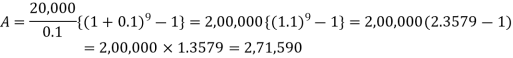
Hence the total required accumulation is 2,71,590 rs.
Example: Rajeev purchased a flat valued at 3,00,000rs. He paid 2,00,000 rs. at the time of purchase and agreed topay the balance with interest of 12% per annum compounded half yearly in 20 equal half yearly installments.
If the first installment is paid after six months from the date of purchase, find the amount of each installment.
[Given log 10.6 = 1.0253 and log 31.19 = 1.494]
Sol.
Here2,00,000 has been paid at the time of purchase when cost of the flat was 3,00,000, we have to
consider 20 equated half yearly annuity payment P when 12% is rate of annual interest compounded half
yearly for present value of 1,00,000rs.
So that-
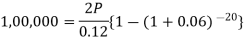
Or
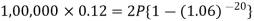
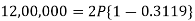
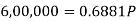
Then-
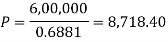
Hence the amount of each installment = 8,718.40
Suppose,
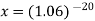
Taking log-
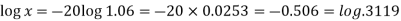
Hence
X = 0.3119
Sinking funds-
A sinking fund is a special type of investment in which a constant amount is invested each year, usually with a view to reaching a specified value at a given point in the future.
Key takeaways-
An annuity is a fixed sum paid at regular intervals under certain conditions.
The length of time during which the annuity is paid can either be until the death of the recipient or for a guaranteed minimum term of years, irrespective of whether the annuitant is alive or not.
2. Amount of an annuity:
Amount of an annuity is the total of all the installments left unpaid together with the compound interest of each payment for the period it remains unpaid.
3. Present value of an annuity-
Present value of an annuity is the sum of the present values of all payments (or installments) made at successive annuity periods
Depreciation-
Depreciation is defined as the expensing of the cost of an asset involved in producing revenues throughout its useful life.
Depreciation expense affects the values of businesses and entities because the accumulated depreciation disclosed for each asset will reduce its book value on the balance sheet. Depreciation expense also affects net income. Generally the cost is allocated as depreciation expense among the periods in which the asset is expected to be used. Such expense is recognized by businesses for financial reporting and tax purposes.
Depreciation does not actually represent any kind of cash transaction. Instead, it simply represents how much of an asset's value has been used up over time and can be deducted as an expense.
The total depreciation over a period of time is known as "accumulated depreciation". The "book value" of an asset is calculated by deducting the accumulated depreciation from the original purchase price. The book value is what is reflected as the asset's value on the balance sheet.
There are four criteria used to calculate depreciation-
1- The initial cost of the asset.
2- The expected residual value (also known as salvage value) - this is the value of asset at the end of its useful life, which may be zero.
3- The estimated useful life of the asset.
4- An appropriate method of apportioning the cost of the useful life of the asset.
Equated monthly instalments-
An equated monthly installment(EMI) is a fixed payment amount made by a borrower to a lender at a specified date e ach calendar month. Equated monthly installments are used to pay off both interest and principal each month so that over a specified number of years, the loan is paid off in full.
Note-
The EMI flat-rate formula is calculated by adding together the principal loan amount and the interest on the principal and dividing the result by the number of periods multiplied by the number of months.
The EMI reducing-balance method is calculated using the formula shown below, in which P is the principal amount borrowed, I is the annual interest rate, r is the periodic monthly interest rate, n is the total number of monthly payments, and t is the number of months in a year.
Example: A man buys a machine for Rs.20,00. What its value be after 6 years, if it is assumed to depreciate at a fixed rate of 12% per annum.
Sol.
Here we have P = 20,000, n = 6 and r = -0.12 (rate of interest is negative in depreciation)
Then,
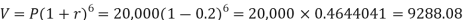
So that the value of the machine in 6 years will be = 9288.08
Example: A machine valued at 500,000 depreciates at 6% per annum then in how many year its value will reduce to 100,000?
Sol. Here P = 500,000, r = 0.06, n = ? and the final value is = 100,000
We know that-

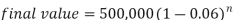
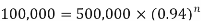
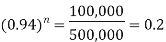
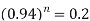
Taking log on both sides-
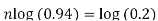
So that-
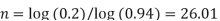
Therefore approximately it will take 26 years for the value decline to 100,000
Example: Ayesha invests Rs. 3000 initially and then Rs. 1800 at the end of the first, second and third years and finally Rs. 600 at the end of 4th year.
If the interest is paid annually at the rate of 6.5% then find the value of the investment at the end of 5th year.
Sol.
Rs. 3000 is invested for 5 years and grows to-
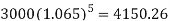
The three sums of Rs. 1800 are invested for 4, 3 and 2 years and grow in total-

And Rs. 600 is invested for 1 year and grows to-
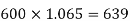
Then the total value at the end of 5 years will be 11,280.81
Key takeaways-
An equated monthly installment(EMI) is a fixed payment amount made by a borrower to a lender at a specified date e ach calendar month. Equated monthly installments are used to pay off both interest and principal each month so that over a specified number of years, the loan is paid off in full.
2. An equated monthly installment (EMI) is a fixed payment made by a borrower to a lender on a specified date of each month.
3. EMIs can be calculated in two ways: the flat-rate method or the reducing-balance method.
4. EMIs allow borrowers the peace of mind of knowing exactly how much money they will need to pay each month toward their loan.
There are two broad types of functions- algebraic and transcendental functions.
Algebraic function: A function in the form of a polynomial with finite number of terms is known as algebraic function.
Domain and Range of a Function:
The set of values of independent variables x is called the ‘Domain’ of the function and the set of corresponding values of f(x) i.e. the dependent variable y is called the ‘Range’ of the function. These functions can be constructed using only a finite number of elementary operations, such as plus, minus, multiplication and division.
Polynomial Function-
A polynomial in the variable x is a function that can be written in the form-

Here  are constant.
are constant.
The term containing the highest power of x are called the leading term
The degree of the polynomial is the power of x in the leading term degree 0, 1, and 2 are polynomials which are constant, linear and quadratic functions while degree 3, 4, and 5 are polynomials with special names: cubic, quartic, and quintic functions. Polynomials with degree n > 5 are just called 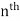 degree polynomials.
degree polynomials.
Constant Function: A constant function is a linear function for which the range does not change no matter which member of the domain is used.
Linear Function: Linear functions are those whose graph is a straight line.
A linear function has the following form. y = f(x) = a + bx.
Quadratic Function: A quadratic function is one of the forms: f(x) = 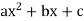 , where a, b, and c are numbers with a ≠ 0
, where a, b, and c are numbers with a ≠ 0
Power Function: A power function is a function that can be represented in
the form:
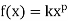
where k and pare real numbers, and x is known as the coefficient
Rational Function-
A rational function is defined by a rational fraction, i.e., an algebraicfraction such that both the numerator and the denominator are polynomials.
Note- the value of denominator should not be equal to zero.
Example: Find the domain and range of the function f(x) = 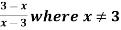
Sol.
f(0) = 3/-3 = -1
f(1) = -1
f(2) = -1
f(3) = -1
so that the domain is = {-1, 0, 1, 2, 4,….} and range = {-1, -1, -1, -1,…..}
Example: find the value of f(2), f(0) and f(3) of the given function-
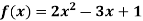
Sol.

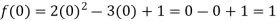
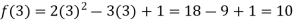
Example: if f(x) =  then prove that
then prove that 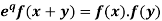
Sol.
By taking LHS-
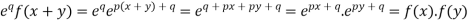
Hence proved
Key takeaways-
Domain and Range of a Function:
A polynomial in the variable x is a function that can be written in the form-
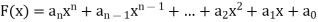
Here 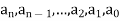 are constant.
are constant.
The term containing the highest power of x are called the leading term
3. Constant Function: A constant function is a linear function for which the range does not change no matter which member of the domain is used.
4. Power Function: A power function is a function that can be represented in
the form:

where k and p are real numbers, and x is known as the coefficient
Permutations-
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are- 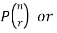
Example 1: Consider the three letters x, y, z. The arrangements of the letter x, y, ztaken two at a time are-
xy, yx, xz, zx, yz, zy
∴The number of 2-arrangements are 6 i.e., the number of permutation of 3 letters taken 2 at a time
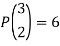
Note-A permutation of n objects taken r at a time is also called r-permutation
Factorial function-
The product of the positive integers from 1 to n is denoted by n!and we read it as “factorial “
Expressed as-

Note- 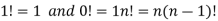
Binomial coefficient-
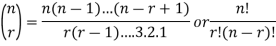
Example:
1. 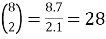

Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any 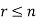 of these objects in a given order is said to be r-permutation.
of these objects in a given order is said to be r-permutation.
The number of permutations of n objects taken r will be denoted as-
P(n, r)
Formula- 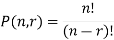
Permutation with repetitions-
The number of permutations of n objects of which are  are alike,
are alike, 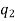 are alike,
are alike, 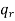
are alike is-
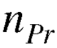
Sampling with or without replacement-
Suppose we chose the samples with repetition, from example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition
Then the product rule tells us that the number of such samples is-
n.n.n.n.n……….n.n = 
And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.
So that in this case the number of samples are given as-
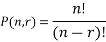
Example-
Three cards are chosen one after the other from a 52-card deck. Find the number m of ways
This can be done: (a) with replacement; (b) without replacement.
Sol.
(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.
(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-
P(52, 3) = 52(51)(50) = 132 600
Example-
There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?
Solution: Total number of balls = 4 black + 3 green + 5 red = 12
The black balls are alike,
The green balls are, and the red balls are alike,
The number of ways in which the balls can be arranged in a row =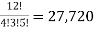
Example- A box contains 10 light bulbs. Find the number n of ordered samples of:
(a) Size 3 with replacement,
(b) Size 3 without replacement.
Solution:
(a) n= 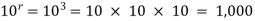
(b) P (10, 3) = 10 × 9 × 8 = 720
Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.
Hence the number of circular permutations of n different objects = (n – 1)!
Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
Note-
1. property-1
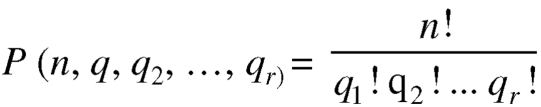
2. property-2
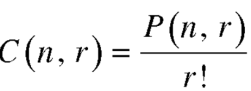
3. property-3
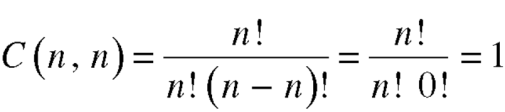
Example: From a class of 3 students, 4 students are to be chosen for competition, in how many ways they can be selected?
Sol.
The number of combinations will be-
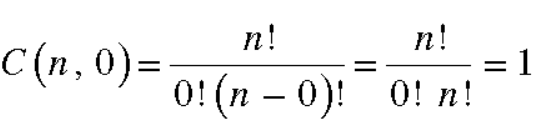
Example:
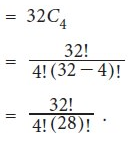
Sol.
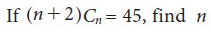
n = -11 is not possible,
therefore-
n = 8
Example:
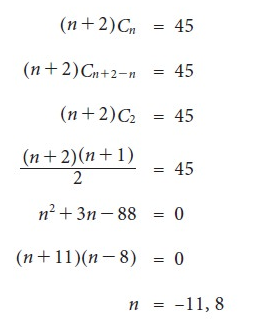
Sol.
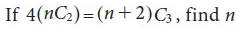
Key takeaways-
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are- 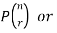
2. Binomial coefficient-
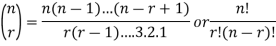
3. Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any 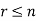 of these objects in a given order is said to be r-permutation.
of these objects in a given order is said to be r-permutation.
4. Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
5. Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
References-