UNIT – 3
WAVE MECHANICS AND ELECTROMAGNETIC THEORY
Quantum mechanics began with two deceptively simple formulas
E=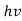 and p= h/λ
and p= h/λ
These are the Einstein and de Broglie relations, respectively.
De Broglie Hypothesis of Matter Waves
As we know in the Photoelectric Effect, the Compton Effect, and the pair production effect—radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal.
In 1923, the French physicist Louis Victor de Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
All material particles should also display dual wave–particle behaviour. That is, the wave–particle duality present in light must also occur in matter.
So, starting from the momentum of a photon p = hν/c = h/λ.
We can generalize this relation to any material particle with nonzero rest mass. Each material particle of momentum 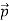 behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector  are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
λ =  =
=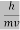 …….(1)
…….(1) 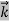 =
=  …….(2)
…….(2)
Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation.
λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment.
However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c.
Therefore
 =
= 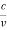 = λ
= λ
Matter waves: According to De-Broglie, a wave is associated with each moving particle which is called matter waves.
That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p = h ν /c = h/λ, we can generalize this relation to any material particle with nonzero rest mass: each material particle of momentum 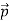 behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector are governed by the speed and mass of the particle.
are governed by the speed and mass of the particle.
λ = 
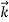 =
= 
Wave has wavelength λ here h is Planck's constant and p is the momentum of the moving particle.
We have seen that microscopic particles, such as electrons, display wave behaviour. What about macroscopic objects? Do they also display wave features? They surely do. Although macroscopic material particles display wave properties, the corresponding wavelengths are too small to detect; being very massive, macroscopic objects have extremely small wavelengths.
At the microscopic level, however, the waves associated with material particles are of the same size or exceed the size of the system. Microscopic particles therefore exhibit clearly noticeable wave-like aspects.
The general rule is: whenever the de Broglie wavelength of an object is in the range of, or exceeds, its size, the wave nature of the object is detectable and hence cannot be neglected.
But if its de Broglie wavelength is much too small compared to its size, the wave behaviour of this object is undetectable.
For a quantitative illustration of this general rule, let us calculate in the following example the wavelengths corresponding to two particles, one microscopic (electron) and the other macroscopic (ball).
DE BROGLIE WAVELENGTH OF MATTER WAVES: IN TERMS OF KINETIC ENERGY AND ASSOCIATED WITH PARTICLE IN THERMAL EQUILIBRIUM
De-Broglie wavelength expressed in term of kinetic energy
If a particle has kinetic energy K.E., then
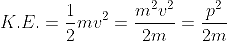
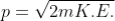
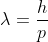
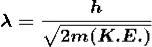
De-Broglie wavelength associated with particle in thermal equilibrium
If the particle is in thermal equilibrium at temperature T, then their kinetic energy is given by
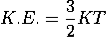
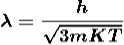
Where K = 1.38 X 10-23 J/K
For an electron
m = 9.1X 10-31 Kg; e = 1.6 X 10-19 C; h = 6.62 X 10-34 J.s
Therefore
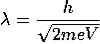
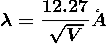
Example: What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?
Solution:
(a)For the electron:
Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s.
Then, momentum
p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s)
p = 4.92 × 10–24 kg m/s
De Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s
λ= 0.135 nm
(b)For the ball:
Mass m’ = 0.150 kg,
Speed v ’= 30.0 m/s.
Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s)
p’= 4.50 kg m/s
De Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m
The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement.
PROPERTIES OF MATTER WAVES
- Matter waves are the waves associated with matter in motion. Wavelength of the matter waves is given by λ=h/p.
- Matter waves are not progressive waves. They are localized waves.
- Matter waves are not single waves. They are group of waves (wave packet) assumed formed due to the superposition of two or more progressive waves.
- Matter waves called pilot waves and they represent the direction of propagation of matter.
- Unlike electromagnetic waves, matter waves will not have constant speed. The speed of matter waves depends on the mass of the particle.
- Vg x Vp=C2 shows that Vp, phase velocity of matter waves is greater than velocity of light. This shows that matter waves not physical waves
- Lighter the particle, greater is the De-Broglie wave length.
- The faster the particle moves, the smaller is its De-Broglie wave length.
- The De-Broglie wave length of a particle in independent of the charge or nature of the particle.
- The matter waves are not electromagnetic in nature. The electromagnetic waves are produced only by charged particle.
Key Takeaways
- Quantum mechanics began with two deceptively simple formula E=
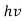 and p= h/λ. These are the Einstein and de Broglie relations respectively.
and p= h/λ. These are the Einstein and de Broglie relations respectively. - De Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
- All material particles should also display dual wave–particle behaviour. That is, the wave–particle duality present in light must also occur in matter.
- The expressions known as the de Broglie relation
λ =  =
=
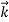 =
= 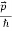
Where ℏ = h/2π. The expression known as the de Broglie relation
Quantum theory and determinism usually do not go together. A natural combination is quantum theory and randomness. Indeed, when in the end of 19th century physics seemed to be close to provide a very good deterministic explanation of all observed phenomena, Lord Kelvin identified “two clouds” on “the beauty and clear-ness of the dynamical theory”. One of this “clouds” was the quantum theory which brought a consensus that there is randomness in physics. Recently we even “certify” randomness using quantum experiments
The quantum theory of the wave function of the Universe is a very successful deterministic theory fully consistent with our experimental evidence. However, it requires accepting that the world we experience is only part of the reality and there are numerous parallel worlds. The existence of parallel worlds allows us to have a clear deterministic and local physical theory.
Wave Function
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as
ψ(x, y, z, t) = a + ib
And its complex conjugate as
ψ*(x, y, z, t) = a – ib.
The product of wave function and its complex conjugate is
ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2
a2 + b2 is a real quantity.
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
- The wave function must be single valued at each point.
- The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.
- ψ must be finite everywhere.
- ψ must be continuous everywhere and
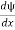 must also be continuous everywhere except where V(x) is infinite.
must also be continuous everywhere except where V(x) is infinite. - ψ (x) must vanish ψ
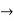 0 as x
0 as x .
. - The wave function should satisfy the normalization condition. Normalization condition of a wave function ψ is mathematical statement of existence of the particle somewhere. So that if we sum up all possible values ∑|ψ(xi,t)|2∆xi we must obtain 1. The total probability of finding the particle anywhere must be one. Normalization condition is given as
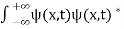 dx =1
dx =1
Only wave function with all these properties can yield physically meaningful result.
Physical significance of wave function
- The wave function ‘Ѱ’ has no physical meaning. It is a complex quantity representing the variation of a matter wave.
- The wave function Ѱ(r,t) describes the position of particle with respect to time .
- It can be considered as ‘probability amplitude’ since it is used to find the location of the particle.
- The square of the wave function gives the probability density of the particle which is represented by the wave function itself.
- More the value of probability density, more likely to find the particle in that region.
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.
All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics.
Statistical Interpretation
It is not possible to measure all properties of a quantum system precisely. Max Born suggested that the wave function was related to the probability that an observable has a specific value.
In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2’. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’ . Thus Ψ2 is a measure of particle density.
According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dxdydz) is given by
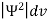 =
= 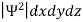
Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space. i.e.
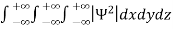 =1
=1
Or 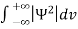 =1
=1
This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function.
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
Key Takeaways
- The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable.
- The wave function must be single valued at each point. The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1. ψ must be finite everywhere.
- According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dxdydz) is given by
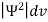 =
= 
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So We have
E= K+V = mv2+V(x) =
mv2+V(x) =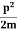 +V(x) ……….. (1)
+V(x) ……….. (1)
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk.
Using this equation (1) for the energy will become
ℏω = 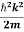 + V(x) ……….. (2)
+ V(x) ……….. (2)
A wave with frequency ω and wave number k can be written as usual as
ψ(x, t) =Aei(kx−ωt) ……….. (3)
The above equation is for one dimensional and for three dimensional we can write it as
ψ(r, t) =Aei(k·r−ωt) ……….. (4)
But here we will stick to one dimension only.
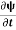 =−iωψ ⇒ ωψ=
=−iωψ ⇒ ωψ=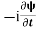 ……….. (5)
……….. (5)
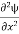 =−k2ψ ⇒ k2ψ = -
=−k2ψ ⇒ k2ψ = - 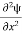 ……….. (6)
……….. (6)
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain
ℏ(ωψ) = 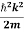 ψ+ V(x) ψ ⇒
ψ+ V(x) ψ ⇒ 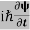 = -
= - 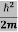
 + V(x) ψ ……….. (7)
+ V(x) ψ ……….. (7)
This is the time-dependent Schrodinger equation.
If we put the x and t in above equation then equation (7) takes the form as given below
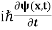 = -
= - 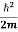
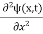 + V(x) ψ(x,t) ……….. (8)
+ V(x) ψ(x,t) ……….. (8)
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the 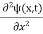 term becomes ∇2ψ.
term becomes ∇2ψ.
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
 = -
= - 
 + V(x) f(x) ……….. (9)
+ V(x) f(x) ……….. (9)
We already know that E=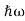 . However ψ(x, t) is general convention to also use the letter ψ to denote the spatial part. So we will now replace f(x) with ψ(x)
. However ψ(x, t) is general convention to also use the letter ψ to denote the spatial part. So we will now replace f(x) with ψ(x)
Eψ = - 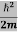
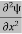 + V(x) ψ ……….. (10)
+ V(x) ψ ……….. (10)
This is called the time-independent Schrodinger equation.
Key Takeaways
- Schrodinger wave equation, is the fundamental equation of quantum mechanics
- The time-dependent Schrodinger equation is given by
⇒ 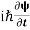 = -
= - 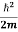
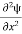 + V(x) ψ
+ V(x) ψ
- The time-independent Schrodinger equation is given by
Eψ = - 
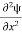 + V(x) ψ
+ V(x) ψ
Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
The potential function is expressed as
V= 0 for 0 ………. (1)
………. (1)
V= 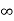 for x <0, x>L ………. (2)
for x <0, x>L ………. (2)

Figure 1: Particle in deep potential well
The probability of finding the particle outside the well is zero (i.e. Ѱ =0)
Inside the well, the Schrödinger wave equation is written as
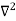 ψ +
ψ +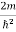 E ψ =0 …………….(2)
E ψ =0 …………….(2)
Substituting 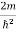 E = k2 …………….(3)
E = k2 …………….(3)
Writing the SWE for 1-D we get
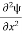 + k2 ψ =0 …………….(4)
+ k2 ψ =0 …………….(4)
The general equation of above equation may be expressed as
ψ = Asin (kx + ϕ) …………….(5)
Where A and ϕ are constants to be determined by boundary conditions
Condition I: We have ψ = 0 at x = 0, therefore from equation
0 = A sinϕ
As A 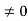 then sinϕ =0 or ϕ=0 …………….(6)
then sinϕ =0 or ϕ=0 …………….(6)
Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5)
0 = Asin kL
As A 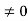 then sinkL =0 or kL=nπ
then sinkL =0 or kL=nπ
k = 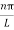 …………….(7)
…………….(7)
Where n= 1,2,3,4………
Substituting the value of k from (7) to (3)
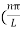 )2 =
)2 = 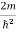 E
E
This gives energy of level
En = 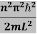 n=1,2,3,4…so on …………….(8)
n=1,2,3,4…so on …………….(8)
From equation En is the energy value (Eigen Value) of the particle in a well.
It is clear that the energy values of the particle in well are discrete not continuous.
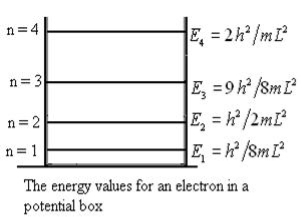
Figure 2: The energy values for an electron in a potential box
Using (6) and (7) equation (5) becomes, the corresponding wave functions will be
ψ = ψn = Asin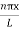 …………….(9)
…………….(9)
The probability density
|ψ(x,t)|2 = ψ ψ*
|ψ(x,t)|2 = A2sin2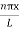 …………….(10)
…………….(10)
The probability density is zero at x = 0 and x = L. Since the particle is always within the well
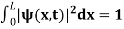 …………….(11)
…………….(11)
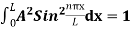
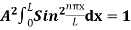
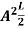 =1
=1
A = 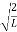
Substituting A in equation (9) we get
ψ = ψn =  sin
sin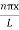 n=1,2,3,4….. …………….(12)
n=1,2,3,4….. …………….(12)
The above equation (12) is normalized wave function or Eigen function belonging to energy value En
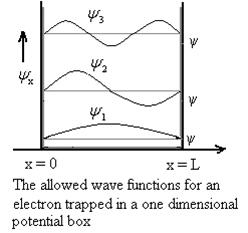 F
F
Figure 3: Wave function for Particle
Key Takeaways
- It is assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
- The probability of finding the particle outside the well is zero (i.e. Ѱ =0)
- The energy values of the particle in well are discrete not continuous and Energy of level is given by
- En =
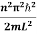 n=1,2,3,4…so on
n=1,2,3,4…so on - The probability density is given by
- |ψ(x,t)|2 = A2sin2

ELECTROSTATICS
Electrostatics, the study of electromagnetic phenomena that occur when there are no moving charges—i.e., after a static equilibrium has been established. Charges reach their equilibrium positions rapidly, because the electric force is extremely strong.
Electrostatics, as the name implies, is the study of stationary electric charges. A rod of plastic rubbed with fur or a rod of glass rubbed with silk will attract small pieces of paper and is said to be electrically charged. The charge on plastic rubbed with fur is defined as negative, and the charge on glass rubbed with silk is defined as positive.
There are some important laws we used in electrostatics.
Coulomb’s Law:
The magnitude of the electric force that a particle exerts on another particle is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. The direction of the force is along the line joining the particles.
Mathematically, the electric force F that a particle of charge q’ exerts on a particle of charge q at a distance r is given by the formula
F =k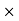
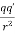
Where k is a constant of proportionality. This formula not only gives the magnitude of the force, but also the direction, if we interpret a positive value of the force F as repulsive and a negative value as attractive.
When a small positive test charge is brought near a large positive charge, it experiences a force directed away from the large charge. If the test charge is far from the large charge, the electrostatic force given by Coulomb's law is smaller than when it is near. This data of direction and magnitude of an electrostatic force, due to a fixed charge or set of fixed charges, constitutes an electrostatic field. The electric field is defined as the force per unit charge exerted on a small positive test charge (q 0) placed at that point. Mathematically,
E = 
Note that both the force and electric field are vector quantities.
Figure 4: is a pictorial representation of the electric fields surrounding a positive charge and a negative charge. These lines are called field lines or lines of force.
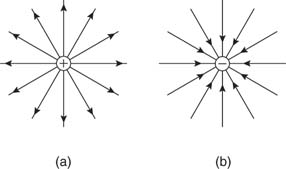
Figure 4: Electric field lines of (a) positive and (b) negative point charges.
Figure 5 shows the electric fields for opposite charges, similar charges, and oppositely charged plates.
Figure 5: Electric field lines of (a) two opposite charges, (b) two like charges, and (c) two oppositely charged plates.
Electric flux
Electric flux is defined as the number of field lines that pass through a given surface. In Figure , lines of electric flux emerging from a point charge pass through an imaginary spherical surface with the charge at its center.
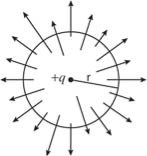
Figure 6: Electric flux
Gauss’s law of electrostatics
The law was published posthumously in 1867 as part of a collection of work by the famous German mathematician Carl Friedrich Gauss.
Gauss’s law for the electric field describes the static electric field generated by a distribution of electric charges.
It states that the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface.
Let’s calculate the electric flux through a spherical surface around a positive point charge q, since we already know the electric field in such a situation. Recall that when we place the point charge at the origin of a coordinate system, the electric field at a point P that is at a distance r
From the charge at the origin is given by
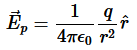
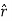 is the radial vector from the charge at the origin to the point P. We can use this electric field to find the flux through the spherical surface of radius r, as shown in Figure 7
is the radial vector from the charge at the origin to the point P. We can use this electric field to find the flux through the spherical surface of radius r, as shown in Figure 7
.
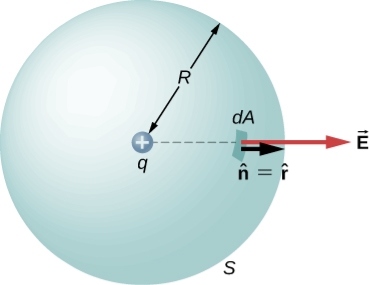
Figure 7: A closed spherical surface surrounding a point charge q.
Then we apply Φ=∫S 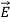 ⋅
⋅ dA
dA
To this system and substitute known values. On the sphere, 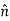 and r=R
and r=R
So for an infinitesimal area dA,
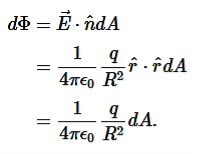
We now find the net flux by integrating this flux over the surface of the sphere
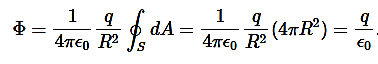
Where the total surface area of the spherical surface is 4πR2. This gives the flux through the closed spherical surface at radius r as
Φ=q/ϵ0
A remarkable fact about this equation is that the flux is independent of the size of the spherical surface. This can be directly attributed to the fact that the electric field of a point charge decreases as 1/r2 with distance, which just cancels the r2 rate of increase of the surface area.
MAGNETISM
Biot-Savart law
The Biot Savart Law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current. Biot–Savart law is consistent with both Ampere’s circuital law and Gauss’s theorem. The Biot-Savart law is fundamental to magnetostatics, playing a role similar to that of Coulomb’s law in electrostatics.
The Biot-Savart law can be stated as:
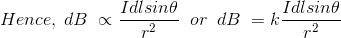 ……….(1)
……….(1)
Where, k is a constant, depending upon the magnetic properties of the medium and system of the units employed.
In the SI system of unit,
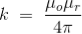 ……….(2)
……….(2)
Therefore, the final Biot-Savart law derivation is,
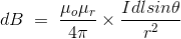 ……….(3)
……….(3)
Ampere’s law
Ampere’s circuital law (ACL) relates current to the magnetic field associated with the current. The magnetic field in space around an electric current is proportional to the electric current which serves as its source, just as the electric field in space is proportional to the charge which serves as its source.
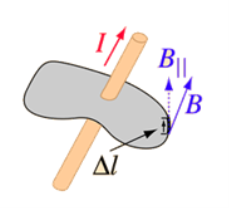
Figure 8: Ampere’s circuital law
Ampere's Law states that
The integral around a closed path of the component of the magnetic field tangent to the direction of the path equals μ0 times the current intercepted by the area within the path.
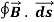 = μ0I ………..(1)
= μ0I ………..(1)
Ampere's Law tells that for any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop.
In order to apply Ampère’s Law
All currents have to be steady (i.e.do not change with time)
Only currents crossing the area inside the path are taken into account and have some contribution to the magnetic field
The total magnetic circulation is zero only in the following cases:-
- The enclosed net current is zero
- The magnetic field is normal to the selected path at any point
- The magnetic field is zero
Finally, be aware that the form of Ampère’s Law addressed here applies to magnetostatics only. In the presence of a time-varying electric field, the right side of ACL includes an additional term known as the displacement current.
Lenz’s Law
Lenz’s law states that the direction of the current induced in a conductor by a changing magnetic field is such that the magnetic field created by the induced current opposes the initial changing magnetic field which produced it.
Lenz’s Law is named after the German scientist H. F. E. Lenz in 1834.
Lenz’s law formula
Lenz’s law states that when an EMF is generated by a change in magnetic flux according to Faraday’s Law, the polarity of the induced EMF is such, that it produces an induced current whose magnetic field opposes the initial changing magnetic field which produced it
The negative sign used in Faraday’s law of electromagnetic induction, indicates that the induced EMF (ε) and the change in magnetic flux (δΦB) have opposite signs. The formula for Lenz’s law is shown below
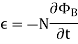
Where:
- ε = Induced emf
- δΦB = change in magnetic flux
- N = Number of turns in coil
Lenz’s law can also be understood as follow. We already know that when a current is induced by a magnetic field, the magnetic field that this induced current produces will create its own magnetic field. This magnetic field will always be such that it opposes the magnetic field that originally created it. In the example below, if the magnetic field “B” is increasing – as shown in (1) – the induced magnetic field will act in opposition to it.
When the magnetic field “B” is decreasing – as shown in (2) – the induced magnetic field will again act in opposition to it. But this time ‘in opposition’ means that it is acting to increase the field – since it is opposing the decreasing rate of change.
Lenz’s law is based on Faraday’s law of induction. Faraday’s law tells us that a changing magnetic field will induce a current in a conductor. Lenz’s law tells us the direction of this induced current, which opposes the initial changing magnetic field which produced it. This is signified in the formula for Faraday’s law by the negative sign (‘–’).
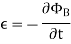
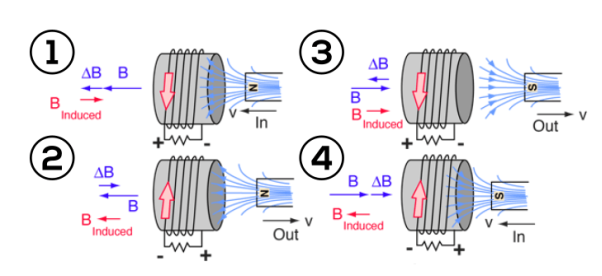
Figure 9: Lenz’s law
This change in the magnetic field may be caused by changing the magnetic field strength by moving a magnet towards or away from the coil, or moving the coil into or out of the magnetic field. In other words, we can say that the magnitude of the EMF induced in the circuit is proportional to the rate of change of flux.
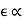
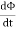
Gauss’s law for magnetism
The Gauss’s law for magnetism states that net flux of the magnetic field through a closed surface is zero because monopoles of a magnet do not exist.
∇·B = 0
FARADAY’S FIRST LAW
Any change in the magnetic field of a coil of wire will cause an emf to be induced in the coil. This emf induced is called induced emf and if the conductor circuit is closed, the current will also circulate through the circuit and this current is called induced current.
Method to change the magnetic field:
- By moving a magnet towards or away from the coil
- By moving the coil into or out of the magnetic field
- By changing the area of a coil placed in the magnetic field
- By rotating the coil relative to the magnet
FARADAY’S SECOND LAW
It states that the magnitude of emf induced in the coil is equal to the rate of change of flux that linkages with the coil. The flux linkage of the coil is the product of the number of turns in the coil and flux associated with the coil.
According to Faraday’s law of electromagnetic induction, the rate of change of flux linkage is equal to induced emf.
 ………..(9)
………..(9)
Considering Lenz’s Law
Where:
- Flux Φ in Wb = B.A
- B = magnetic field strength
- A = area of the coil
Key Takeaways
- Coulomb’s Law states that the magnitude of the electric force that a particle exerts on another particle is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. The direction of the force is along the line joining the particles.
- Electric flux is defined as the number of field lines that pass through a given surface.
- Gauss’s law of electrostatics states that the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface.
- The Biot Savart Law relates the magnetic field to the magnitude, direction, length, and proximity of the electric current. The Biot-Savart law can be stated as:

- Ampere's Law states that the integral around a closed path of the component of the magnetic field tangent to the direction of the path equals μ0 times the current intercepted by the area within the path.
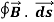 = μ0I
= μ0I - Lenz’s law states that the direction of the current induced in a conductor by a changing magnetic field is such that the magnetic field created by the induced current opposes the initial changing magnetic field which produced it.
- Faraday’s law states that the magnitude of emf induced in the coil is equal to the rate of change of flux that linkages with the coil.
- The flux linkage of the coil is the product of the number of turns in the coil and flux associated with the coil.
Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.
From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization.
We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed.
Maxwell’s four equations are given by
∇·E = ρ/ε0 (1)
∇×E = −∂B/∂t (2)
∇×H = J + ∂D/∂t (3)
∇·B = 0 (4)
These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,
∇=(∂/∂x, ∂/∂y, ∂/∂z)
E is the electric vector
B is the magnetic induction
ρ is the electric charge density
j is the electric current density
ε0 is the permittivity of free space
c is the speed of light.
In addition to Maxwell equations, the following identities are useful:
J = σE (5)
D = εE (6)
B = μH (7)
Here,
D is the electric displacement
H is the magnetic vector
σ is the specific conductivity
ε is the dielectric constant (or permittivity)
μ is the magnetic permeability
In the Gaussian systems of units, Maxwell equations are given in the form of
∇·B=0 (8)
∇·E=4πρ (9)
∇×H=(1/c)(∂D/∂t+4πj) (10)
∇×E=−(1/c)(∂B/∂t) (11)
Free space or non-conducting medium. We know that non conducting medium means no current so conductivity is zero i.e. σ=0
So current density J=σE will also become zero as σ=0 Also free space means no charges which leads to ρ=0. These points mentioned below.
(a) No condition current i.e σ=0, thus J=0 ( J=σE)
(b) No charges (i.e ρ=0)
For the case of no charges or currents, that is, j = 0 and ρ = 0, and a homogeneous medium. Using these the Maxwell equation can rewritten as
∇.D=0 or ∇.E=0 as ρ=0 (12)
∇ x E= -dB/dt or ∇ x E= -μ dH/dt because B = μH (13)
∇ x H=d D/dt or ∇ x H = ε dE/dt (J=0) and D = εE (14)
∇.B=0 (15)
Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects.
Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.
These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.
From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization.
The First Maxwell’s equation (Gauss’s law for electrostatics)
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
∇·E = ρ/ε0
0r
∇·D = ρ
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
The Gauss’s law states that flux passing through any closed surface is equal to 1/ε0 times the total charge enclosed by that surface.
Integral form of Maxwell’s 1st equation
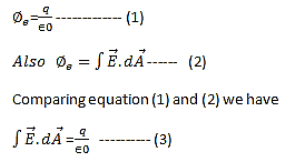
It is the integral form of Maxwell’s 1st equation.
Maxwell’s first equation in differential form
It is called the differential form of Maxwell’s 1st equation.

The Second Maxwell’s equation (Gauss’s law for magnetism)
The Gauss’s law for magnetism states that net flux of the magnetic field through a closed surface is zero because monopoles of a magnet do not exist.

We know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero.
Why? Why isn't the divergence of B equal to the magnetic charge density?
Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero:
∇·B = 0
Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.
Maxwell’s Third equation (Faraday's Law)
Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.
Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.
∇×E = −∂B/∂t
According to Faraday’s law of electromagnetic induction

It is the differential form of Maxwell’s third equation.
Maxwell’s fourth equation (Ampere's Law)
Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced.
This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon.
The modified form of ampere Law is given by
H.dL=(J+dD/dt)
Take integration on both sides we have
∫H.dL=∫(J+dD/dt).dS
Apply stoke’s theorem to L.H.S. Of above equation, we get
∫( ∇xH).dS=∫ H.dL
Now the above equation is written as
∫( ∇xH).dS =∫(J+dD/dt).dS
By cancelling the surface integral on both sides we have
∇xH =J+dD/dt
Which is the differential form of Maxwell’s equation.
This can also be written in the form B
The Ampere-Maxwell Law
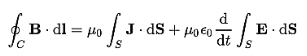
Begin with the Ampere-Maxwell law in integral form.
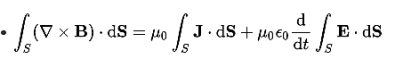
Invoke Stokes' theorem.
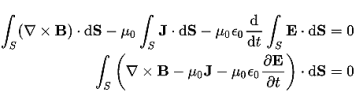
Set the equation to 0. 
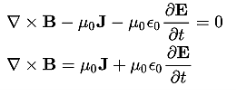
Physical Significance Of Each Equation
Physical significance of Maxwell’s Ist equation
∇·E = ρ/ε0
According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.
Physical significance of Maxwell’s 2nd equation
∇·B = 0
It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.
Physical significance of Maxwell’s 3rd equation
∇×E = −∂B/∂t
It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.
Physical significance of Maxwell’s 4th equation
∇×H = J + ∂D/∂t
This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current density and displacement current density.
Key Takeaways
- The First Maxwell’s equation is known as Gauss’s law for electrostatics. It is given by ∇·E = ρ/ε0 . According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics,
- The Second Maxwell’s equation is known as Gauss’s law for magnetism. . It is given by ∇·B = 0. The Gauss’s law for magnetism states that net flux of the magnetic field through a closed surface is zero because monopoles of a magnet do not exist.
- Maxwell’s Third equation is known as Faraday's Law. It is given by ∇×E = −∂B/∂t. Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit.
- Maxwell’s fourth equation is known as Ampere's Law. It is given by ∇×H = J + ∂D/∂t .Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current.
CONDUCTION
Conduction in metals and n-type semiconductors involves free electrons moving many atomic diameters before they lose momentum by interacting with atoms or other particles. Acceleration induced by the small applied electric field inside the conductor restores electron velocities to produce equilibrium current. The total current density J [Am-2] is proportional to the product of the average electron velocity v [ms-1] and the number density n [m-3] of free electrons. A related conduction process occurs in ionic liquids, where both negative and positive ions can carry charge long distances.
In metals there is approximately one free electron per atom and in warm n-type semiconductors there is approximately one free electron per donor atom, where the sparse donor atoms are easily ionized thermally. Since, for non-obvious reasons, the average electron velocity 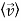 is proportional to
is proportional to 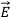 , therefore
, therefore 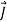 =−en
=−en = σ
= σ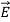 . As the conductivity σ approaches infinity the electric field inside a conductor approaches zero for any given current density
. As the conductivity σ approaches infinity the electric field inside a conductor approaches zero for any given current density 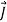 .
.
Warm donor atoms in n-type semiconductors can be easily ionized and contribute electrons to the conduction band where they move freely. Only certain types of impurity atoms function as donors those that are most easily ionized. As the density of donor atoms approaches zero and as temperature declines, the number of free electrons and the conductivity approach very low values that depend on temperature and any alternative ionization mechanisms that are present.
In p-type semiconductors the added impurity atoms readily trap nearby free electrons to produce a negative ion; this results in a corresponding number of positively ionized semiconductor atoms that act as “holes”. As a result any free electrons typically move only short distances before they are trapped by one of these holes. Moreover, the threshold energy required to move an electron from a neutral atom to an adjacent positive ion is usually less than the available thermal energy, so such transfers occur rapidly, causing the hole to move quickly from place to place over long distances. Thus holes are the dominant charge carriers in p-type semiconductors, whereas electrons dominate in n-type semiconductors.
More broadly, semiconductors have a conduction band in which free electrons can propagate long distances; this band is separated by energy of one or a few electron volts from the valence band in which electrons cannot move. The conduction band is not a location, it is a family of possible electron wave states. When electrons are excited from the valence band to the conduction band by some energetic process, they become free to move in response to electric fields.
Semiconductor conductivity is approximately proportional to the number of free electrons or holes produced by the scarce impurity atoms, and therefore to the doping density of those impurity atoms. Easily ionized impurity atoms are the principal mechanism by which electrons enter the conduction band, and impurities that readily trap adjacent electrons are the principal mechanism by which holes enter and move in the valence band.
The current leakage processes in insulators imprecisely resemble electron and hole conduction in semiconductors, and can include weak surface currents as well as bulk conduction; microscopic flaws can also increase conductivity. The conductivities of typical materials are listed in Table 1.
Table 1: Nominal conductivities σ of common materials [Siemens m-1]

In some exotic materials the conductivity is a function of direction and can be represented by the 3×3 matrix σ; such materials are not addressed here. Some materials exhibit superconductivity, or infinite conductivity. In these materials pairs of electrons become loosely bound magnetically and move as a unit called a Cooper pair.
Quantum mechanics prevents these pairs from colliding with the lattice and losing energy. Because the magnetic binding energy for these pairs involves electron spins, it is quite small. Normal conductivity returns above a threshold critical temperature at which the pairs are shaken apart, and it also returns above some threshold critical magnetic field at which the magnetic bonds coupling the electrons break as the electron spins all start to point in the same direction. Materials having critical temperatures above 77K (readily obtained in cryogenic refrigerators) are difficult to achieve.
The finite number of such pairs at any temperature and magnetic field limits the current to some maximum value; moreover that current itself produces a magnetic field that can disrupt pairs. Even a few pairs can move so as to reduce electric fields to zero by short-circuiting the normal electrons until the maximum current carrying capacity of those pairs is exceeded. If the applied fields have frequency f > 0, then the Cooper pairs behave much like collision less electrons in plasma and therefore the applied electric field can penetrate that plasma to its skin depth. Those penetrating electric fields interact - with a small number of normal electrons to produce tiny losses in superconductors that increase with frequency.
DISPLACEMENT CURRENT
Displacement current is the rate of change of electric displacement field.
The type of current which passes through a conductor is known as conduction current and is caused by the actual movement of electrons through the conductor. This type of current is mostly used in our day to day life. There is also another kind of current, which is known as displacement current. Displacement current differs from the conduction current because the displacement current does not involve electrons' movement. The displacement current has enormous importance for the propagation of electromagnetic waves. In electromagnetism, displacement current is a quantity appearing in Maxwell's equations that is defined in terms of the rate of change of electric displacement field.
Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do.
It is mathematically represented as
ID = JD S = S 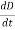
Where
S = Area of the plate of the capacitor
ID = Displacement current
JD = Displacement current density
D = εE where ε is permittivity of the medium
During the charging and discharging process of the capacitor, the electric current flows through the wires of the circuit. However, no current flow between the plates of the capacitor.
Key Takeaways
- Conduction in metals and n-type semiconductors involves free electrons moving many atomic diameters before they lose momentum by interacting with atoms or other particles.
- Displacement current is the rate of change of electric displacement field.
- Displacement current differs from the conduction current because the displacement current does not involve electrons' movement.
- The displacement current has enormous importance for the propagation of electromagnetic waves.
- Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do.
The permittivity εo of free space is 8.854×10-12 farads/meter, where
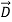 =εo
=εo 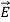 .
.
The permittivity ε of any material deviates from εo for free space if applied electric fields induce electric dipoles in the medium; such dipoles alter the applied electric field seen by neighbouring atoms.
Electric fields generally distort atoms because  pulls on positively charged nuclei (f=q
pulls on positively charged nuclei (f=q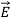 [N]) and repels the surrounding negatively charged electron clouds. The resulting small offset d of each atomic nucleus of charge +q relative to the center of its associated electron cloud produces a tiny electric dipole in each atom, as suggested in Figure: 10(a).
[N]) and repels the surrounding negatively charged electron clouds. The resulting small offset d of each atomic nucleus of charge +q relative to the center of its associated electron cloud produces a tiny electric dipole in each atom, as suggested in Figure: 10(a).
In addition, most asymmetric molecules are permanently polarized, such as H2O or NH3, and can rotate within fluids or gases to align with an applied field. Whether the dipole moments are induced, or permanent and free to rotate, the result is a complete or partial alignment of dipole moments as suggested in Figure: 10(b).
These polarization charges generally cancel inside the medium, as suggested in Figure: 10(b), but the immobile atomic dipoles on the outside surfaces of the medium are not fully cancelled and therefore contribute the surface polarization charge ρsp
Figure 10: Polarized media
Figure:10(c) suggests how two charged plates might provide an electric field  that polarizes a dielectric slab having permittivity ε > εo. The electric field
that polarizes a dielectric slab having permittivity ε > εo. The electric field  is the same in vacuum as it is inside the dielectric (assuming no air gaps) because the path integral of
is the same in vacuum as it is inside the dielectric (assuming no air gaps) because the path integral of 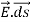 from plate to plate equals their voltage difference V in both cases. The electric displacement vector
from plate to plate equals their voltage difference V in both cases. The electric displacement vector 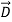 e =ε
e =ε 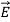 and therefore differs.] We associate the difference between
and therefore differs.] We associate the difference between 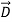 o =εo
o =εo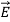 (vacuum) and
(vacuum) and 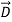 ε=ε
ε=ε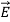 (dielectric) with the electric polarization vector P , where:
(dielectric) with the electric polarization vector P , where:
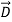 = ε
= ε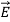 =εo
=εo 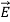 +
+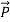 = εo
= εo 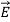 (1+
(1+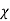 ) (8)
) (8)
The polarization vector 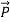 is defined by (8) and is normally parallel to
is defined by (8) and is normally parallel to 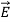 in the same direction, as shown in Figure: 10(c); it points from the negative surface polarization charge to the positive surface polarization charge (unlike
in the same direction, as shown in Figure: 10(c); it points from the negative surface polarization charge to the positive surface polarization charge (unlike  , which points from positive charges to negative ones).
, which points from positive charges to negative ones).
As suggested in (8), 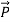 = εo
= εo 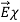 ,
,
Where χ is defined as the dimensionless susceptibility of the dielectric. Because nuclei are bound rather tightly to their electron clouds, χ is generally less than 3 for most atoms, although some molecules and crystals, particularly in fluid form, can exhibit much higher values.
Electric displacement, also known as dielectric displacement and usually denoted by D, is a vector field in a non-conducting medium, a dielectric.
In a dielectric material, the presence of an electric field E causes the bound positive and negative charges in the material to slightly separate, inducing a local electric dipole moment. The electric displacement field "D" is defined as
D= 𝜺0E+P
D =
Electric displacement
E = External electric field in which the dielectric is placed
𝜺0 = the permittivity of the free space
P = Polarization Density
In S.I. System, Unit of Electric displacement is C/m2.
D =  E+P
E+P
D= 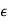 E and P =
E and P = 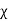 eE
eE
Key Takeaways
- The permittivity εo of free space is 8.854×10-12 farads/meter
- The electric displacement vector
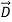 e =ε
e =ε 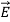 and therefore differs.] We associate the difference between
and therefore differs.] We associate the difference between 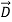 o =εo
o =εo (vacuum) and
(vacuum) and  ε=ε
ε=ε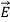 (dielectric) with the electric polarization vector P , where:
(dielectric) with the electric polarization vector P , where: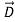 = ε
= ε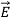 =εo
=εo 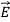 +
+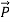 = εo
= εo  (1+
(1+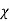 )
) - The electric displacement field "D" is defined as D= 𝜺0E+P
In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature.
Maxwell proved that both the electric and magnetic fields are perpendicular to each other in the direction of wave propagation. He considered an electromagnetic wave propagating along positive x-axis. When a rectangular parallelepiped was placed parallel to the three co-ordinate axis, the electric and magnetic fields propagate sinusoidal with the x-axis and are independent of y and z-axis.
A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.
Solutions of Maxwell’s Equations - Uniform Plane Waves
The sources of time varying electromagnetic fields are time varying charges and currents, whether man-made or naturally occurring. However, examination of Maxwell’s equations shows that, even in empty space (with no sources), and fields cause each other. This means that, although these fields must originate in source regions, they can propagate through source-free regions. Because solutions in source regions are very hard to obtain, let us consider what kind of fields can exist in source-free regions.
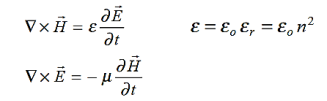
These equations are still very complicated (4 different partial derivatives). Let’s try to find simple solutions. We do this by making assumptions. After finding simplest solutions, we:
(i) Find what kind of source would generate this type of field (waves).
(ii) Show that these simple solutions are useful approximations to real electromagnetic waves.
Assumption for Solution:
Can we find a solution such that:
1.) No variation exists in x and y directions.
2.) 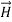 or
or 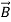 also is oriented along one of the axes.
also is oriented along one of the axes.
Ampere’s Law becomes:
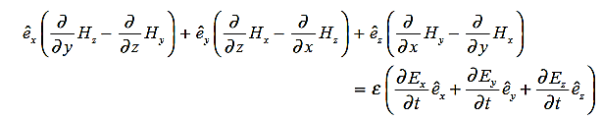
Or, with our assumptions:
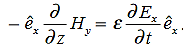
Compare for transmission line:
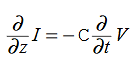
In a similar manner,
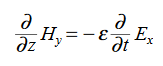 ………….(1)
………….(1)
Faraday’s Law becomes:
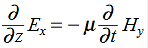 ………….(2)
………….(2)
Thus, if  is only in the
is only in the  direction, then is only in the .If we differentiate (2) with respect to z, we get:
direction, then is only in the .If we differentiate (2) with respect to z, we get:
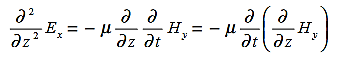
Substitute from (2),
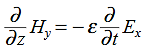
We get
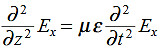
This is called the wave equation.
Compare for transmission line: (same).
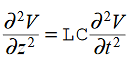
We will assume dielectric media; lossless:
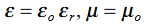
Dimensional analysis:
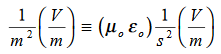
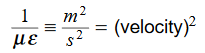
In the units we are using:
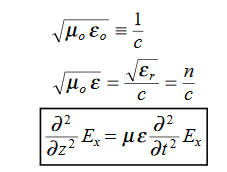
By exactly the same method, we also get:
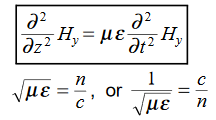
For example, the same equation is true for  and
and  . Thus,
. Thus,  and
and 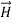 must have the same type of functional dependence. This wave equation still has many possible solutions. In fact, it can be shown by direct substitution that
must have the same type of functional dependence. This wave equation still has many possible solutions. In fact, it can be shown by direct substitution that
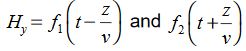
Are the solutions
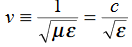
t is important to note that f1 and f2 can be any function.
The field we find directly from the equation:
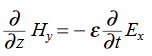
Suppose
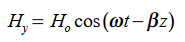 …………(3)
…………(3)
Differentiate (3) with respect to z
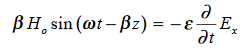 …………(4)
…………(4)
Integrate with respect to time
 …………(5)
…………(5)
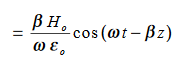
This leads to a new quantity that relates the electric and magnetic fields:
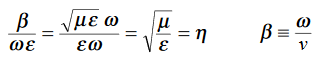
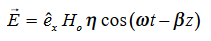
Rewriting:
Units of 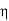 =
=  =
=  = Ω
= Ω
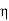 0 = Impedance of free space =
0 = Impedance of free space = 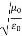 =377 Ω
=377 Ω
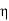 = impedance of a lossless dielectric =
= impedance of a lossless dielectric = 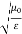 =
=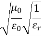 =
= 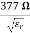
Note that 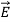 and
and 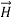 are in time phase and space quadrature
are in time phase and space quadrature
The directions of the vectors are such that:
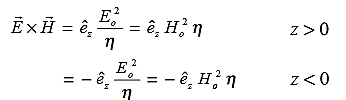
This vector 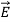
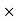
 , always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves.
, always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves.
“Plane” refers to the fact that, at any instant in time, the surfaces of constant phase are planes (here, constant).
“Uniform” means no variation in transverse direction. The wave derived here is one oscillating at a single frequency. The frequency is determined by the source. If the source has multiple frequencies, so will the wave. In communications, modulating a carrier wave results in multiple frequencies. But before we can study such fields, we must thoroughly understand single frequency sinusoidal waves.
Key Takeaways
- A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.
- This vector
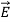

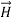 , always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves.
, always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves.
When electromagnetic wave travels in space, it carries energy and energy density is always associated with electric fields and magnetic fields.
The rate of energy travelled through per unit area i.e. the amount of energy flowing through per unit area in the perpendicular direction to the incident energy per unit time is called Poynting vector.
Mathematically Poynting vector is represented as
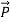 =
= 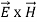 =(
=( 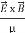 ) (i)
) (i)
The direction of Poynting vector is perpendicular to the plane containing 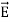 and
and 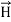 . Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer
. Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer 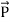 is perpendicular to both
is perpendicular to both 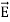 and
and . It represents the rate of energy transfer per unit area.
. It represents the rate of energy transfer per unit area.
UNIT
Its unit is W/m2.
Poynting Theorem
Poynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses.
i.e. total power leaving the volume =Rate of decrease of stored electromagnetic energy – ohmic power dissipated due to motion of charge
Proof
The energy density carried by the electromagnetic wave can be calculated using Maxwell's equations
Div 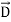 = 0 ...(i)
= 0 ...(i)
Div 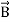 =0 ...(ii)
=0 ...(ii)
Curl 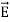 = -
= - 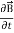 …(iii)
…(iii)
Curl 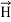 =
=  +
+ 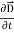 …(iv)
…(iv)
Taking scalar product of (3) with H and (4) with 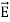
i.e. 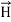 curl
curl  = -
= - 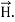
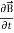 ……(v)
……(v)
And 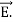 curl
curl 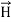 =
= 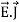 +
+ 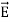 .
. 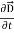 …..(vi)
…..(vi)
Doing (vi) – (v) i.e.

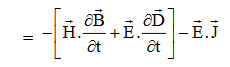
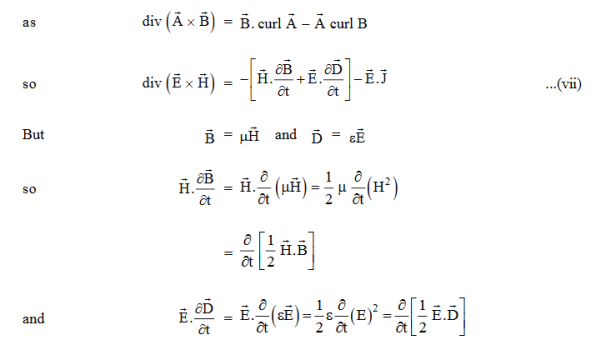
So from equation (vii)
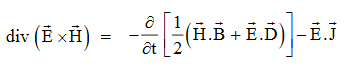
Or

Integrating equation (viii) over a volume V enclosed by a Surface S
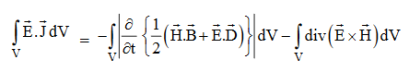
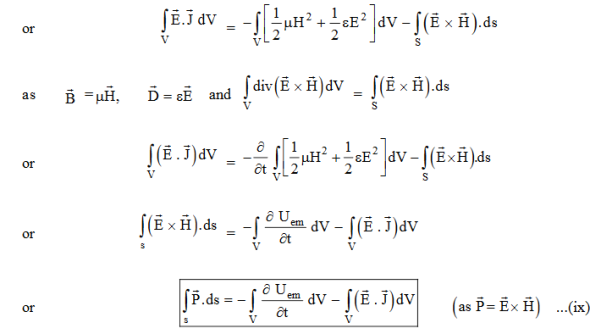
Total power leaving the volume = rate of decrease of stored e.m. Energy -ohmic power dissipated due to charge motion
This equation (ix) represents the Poynting theorem according to which the net power flowing out of a given volume is equal to the rate of decrease of stored electromagnetic energy in that volume minus the conduction losses.
In equation (ix) 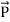 .ds represents the amount of electromagnetic energy crossing the closed surface per second or the rate of flow of outward energy through the surface S enclosing volume V i.e. it is Poynting vector.
.ds represents the amount of electromagnetic energy crossing the closed surface per second or the rate of flow of outward energy through the surface S enclosing volume V i.e. it is Poynting vector.
The term represent
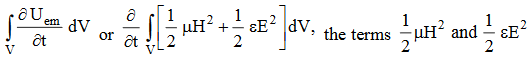
The energy stored in electric and magnetic fields respectively and their sum denotes the total energy stored in electromagnetic field. So total terms gives the rate of decrease of energy stored in volume V due to electric and magnetic fields.
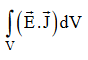
Gives the rate of energy transferred into the electromagnetic field.
This is also known as work-energy theorem. This is also called as the energy conservation law in electromagnetism.
Key Takeaways
- The rate of energy travelled through per unit area i.e. the amount of energy flowing through per unit area in the perpendicular direction to the incident energy per unit time is called Poynting vector.
- Mathematically Poynting vector is represented as
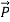 =
= 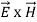 =(
=(  )
) - The direction of Poynting vector is perpendicular to the plane containing
 and
and 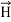 .
. - Poynting vector is also called as instantaneous energy flux density. It represents the rate of energy transfer per unit area.
- Its unit is W/m2.
References
- Richard Robinett, Quantum Mechanics
- Quantum Mechanics Concepts & Applications -- Nouredine Zettili
- Introduction to Quantum Mechanics -- David J Griffiths
- Quantum Physics -- H.C.Verma
- Introduction to Electrodynamics, David Griffiths, 4th Ed, Cambridge University Press 2017.
- Engineering physics- Gaur and Gupta, & S.Chand Publication
- Engineering physics - Avadhanalu and Kshirsagar, S.Chand Publication