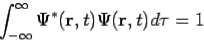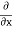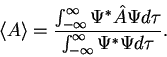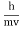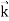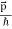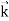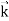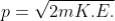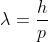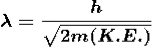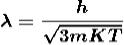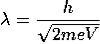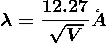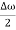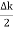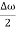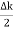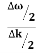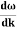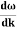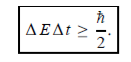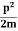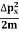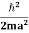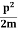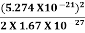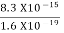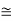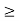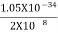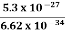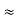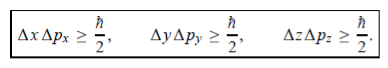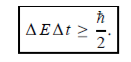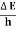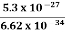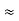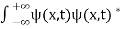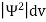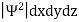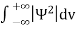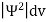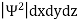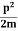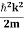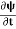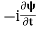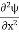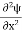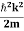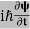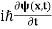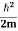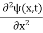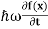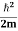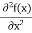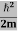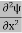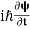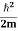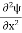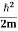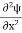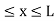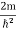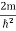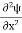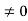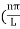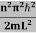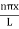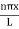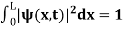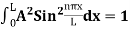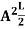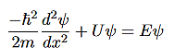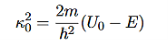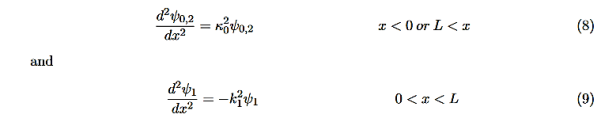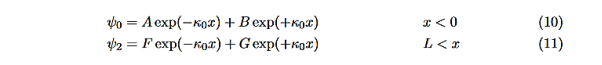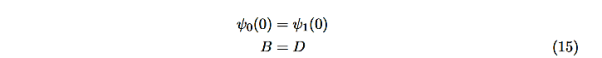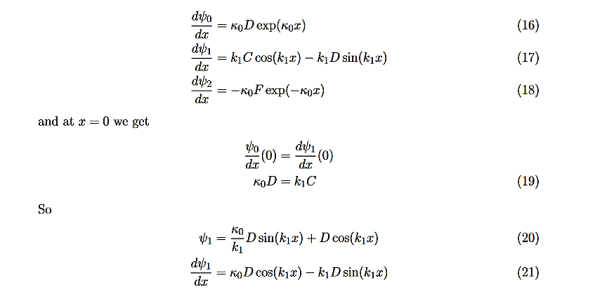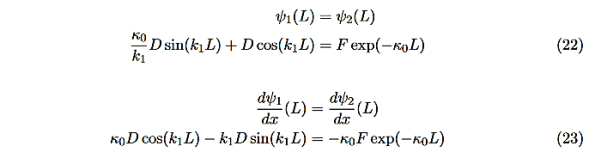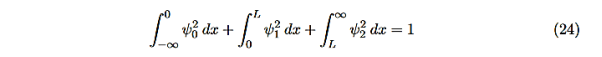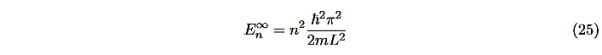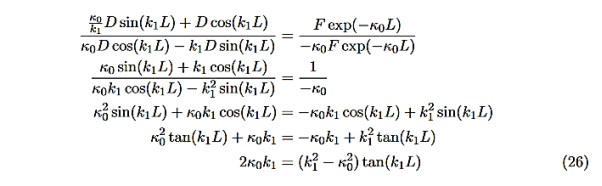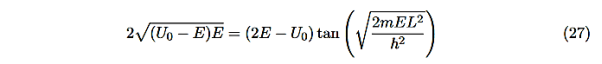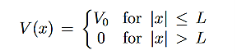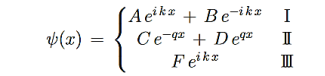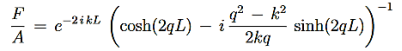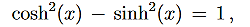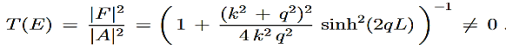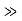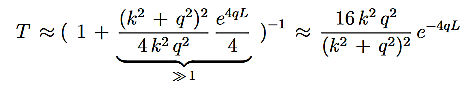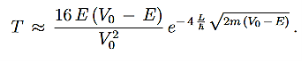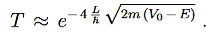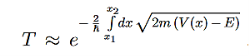UNIT – 1
Quantum Theory
If the systems of quantum theory are thought of as elementary information carriers in the first place, rather than elementary constituents of matter, and their connections are logical connections within a given algorithm, rather than space-time relations, then we need to find the origin of mechanical concepts that characterise quantum mechanics as a theory of physical systems. To this end, we will illustrate how physical laws can be viewed as algorithms for the update of memory registers that make a physical system.
The term "quantum mechanics" was first coined by Max Born in 1924.
Quantum mechanics is the branch of physics dealing with the behaviour of matter and light on the atomic and subatomic level. . It attempts to describe and account for the properties of molecules and atoms and their constituents—electrons, protons, neutrons, and other more particles such as quarks and gluons.
At the scale of atoms and electrons, many of the equations of classical mechanics which describe how things move at everyday sizes and speeds cease to be useful.
In classical mechanics objects exist in a specific place at a specific time. However, in quantum mechanics, objects instead exist in a haze of probability they have a certain chance of being at point A another chance of being at point B and so on. It results some very strange conclusions about the physical world.
At the turn of the twentieth century, however, classical physics not able to explain some of the phenomena.
Relativistic domain: Einstein’s 1905 theory of relativity showed that the validity of
Newtonian mechanics ceases at very high speeds i.e. Speeds comparable to that of light.
Microscopic domain: As soon as new experimental techniques were developed to the point of searching atomic and subatomic structures, it turned out that classical physics fails miserably in providing the proper explanation for several newly discovered phenomena. It thus became evident that the validity of classical physics ceases at the microscopic level and that new concept had needed to describe.
The classical physics fails to explain several microscopic phenomena such as blackbody radiation, the photoelectric effect, atomic stability and atomic spectroscopy
In 1900 Max Planck introduced the concept of the quantum of energy. He successfully explained the phenomenon of blackbody radiation. He introduced the concept of discrete or quantized Energy. He also explained that the energy exchange between an electromagnetic wave of frequency ν and matter occurs only in integer multiples of hν, which he called the energy of a quantum, where h is called Planck’s constant.
In 1905 Einstein provided a powerful consolidation to Planck’s quantum concept. In trying to understand the photoelectric effect, Einstein recognized that Planck’s idea of the quantization of the electromagnetic waves must be valid for light as well.
So, He Gave light itself is made of discrete bits of energy or tiny particles, called photons, each of energy hν, ν being the frequency of the light. The introduction of the photon concept enabled Einstein to give an elegantly accurate explanation to the photoelectric problem.
Bohr introduced in 1913 his model of the hydrogen atom. He explained that atoms can be found only in discrete states of energy and the emission or absorption of radiation by atoms, takes place only in discrete amounts of hν. This successfully explained to problems such as atomic stability and atomic spectroscopy
Then in 1923 Compton made an important discovery of scattering X-rays with electrons, he confirmed that the X-ray photons behave like particles with momenta hν/c, ν is the frequency of the X-rays.
Planck, Einstein, Bohr, and Compton gave the theoretical and experimental confirmation for the particle aspect of wave that means that waves exhibit particle behaviour at the microscopic scale.
Some of the most prominent scientists to subsequently contribute in the mid-1920s to what is now called the "new quantum mechanics" or "new physics" were Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, and Erwin Schrödinger.
Through a century of experimentation and applied science, quantum mechanical theory has proven to be very successful and practical.
Historically, there were two independent formulations of quantum mechanics. The first formulation, called matrix mechanics, was developed by Heisenberg (1925) to describe atomic structure starting from the observed spectral lines.
The second formulation, called wave mechanics, was due to Schrödinger (1926).
It is a generalization of the de Broglie postulate. This method describes the dynamics of microscopic matter by means of a wave equation, called the Schrodinger equation.
Dirac derived in 1928 an equation which describes the motion of electrons. This equation, known as Dirac’s equation, predicted the existence of an antiparticle.
In short, quantum mechanics is the founding basis of all modern physics: solid state, molecular, atomic, nuclear, and particle physics, optics, thermodynamics, statistical mechanics, and so on. Not only that, it is also considered to be the foundation of chemistry and biology.
Postulates of Quantum Mechanics
- The state of a quantum mechanical system is completely specified by a function (r,t) that depends on the coordinates of the particle(s) and on time. This function, called the wave function or state function, has the important property that *(r,t) (r,t)d
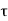 is the probability that the particle lies in the volume element d
is the probability that the particle lies in the volume element d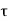 located at r at time t
located at r at time t
The wavefunction must satisfy certain mathematical conditions because of this probabilistic interpretation. For the case of a single particle, the probability of finding it somewhere is 1, so that we have the normalization condition
|
It is customary to also normalize many-particle wavefunctions to 1. The wavefunction must also be single-valued, continuous, and finite.
2. To every observable in classical mechanics, there corresponds a linear, Hermitian operator in quantum mechanics. For example, in coordinate space, the momentum operator 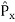 corresponding to momentum px in the
corresponding to momentum px in the 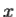 direction for a single particle is
direction for a single particle is
iℏ |
3. The average value of the observable corresponding to operator 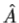 is given by
is given by
|
4. The wavefunction evolves in time according to the time-dependent Schrödinger equation.
|
5. In any measurement of the observable associated with operator 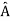 , the only values that will ever be observed are the eigenvalues a which satisfy
, the only values that will ever be observed are the eigenvalues a which satisfy 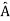 = a. Although measurements must always yield an eigenvalue, the state does not originally have to be in an eigenstate of
= a. Although measurements must always yield an eigenvalue, the state does not originally have to be in an eigenstate of 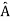 . An arbitrary state can be expanded in the complete set of eigenvectors of
. An arbitrary state can be expanded in the complete set of eigenvectors of 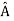 (
(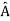 = a) as, =
= a) as, = 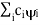 where the sum can run to infinity in principle. The probability of observing eigenvalue ai is given by ci*ci.
where the sum can run to infinity in principle. The probability of observing eigenvalue ai is given by ci*ci.
6. The total wavefunction must be antisymmetric with respect to the interchange of all coordinates of one fermion with those of another. Electronic spin must be included in this set of coordinates. The Pauli Exclusion Principle is a direct result of this antisymmetry principle.
Key Takeaways
- The term "quantum mechanics" was first coined by Max Born in 1924.
- Quantum mechanics is the branch of physics dealing with the behaviour of matter and light on the atomic and subatomic level. .
- It attempts to describe and account for the properties of molecules and atoms and their constituents—electrons, protons, neutrons, and other more particles such as quarks and gluons.
- The introduction of the photon concept enabled Einstein to give an elegantly accurate explanation to the photoelectric problem.
- The state of a quantum mechanical system is completely specified by a function
Einstein Equation
Quantum mechanics began with two deceptively simple formulas
E=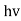 and p= h/λ
and p= h/λ
These are the Einstein and de Broglie relations, respectively.
De Broglie Hypothesis of Matter Waves
As we know in the Photoelectric Effect, the Compton Effect, and the pair production effect—radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal.
In 1923, the French physicist Louis Victor de Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
All material particles should also display dual wave–particle behaviour. That is, the wave–particle duality present in light must also occur in matter.
So, starting from the momentum of a photon p = hν/c = h/λ.
We can generalize this relation to any material particle with nonzero rest mass. Each material particle of momentum 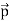 behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector 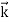 are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
λ = |
Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation.
λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment.
However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c.
Therefore
|
Matter waves: According to De-Broglie, a wave is associated with each moving particle which is called matter waves.
That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p = h ν /c = h/λ, we can generalize this relation to any material particle with nonzero rest mass: each material particle of momentum 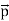 behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector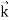 are governed by the speed and mass of the particle.
are governed by the speed and mass of the particle.
λ = |
Wave has wavelength λ here h is Planck's constant and p is the momentum of the moving particle.
We have seen that microscopic particles, such as electrons, display wave behaviour. What about macroscopic objects? Do they also display wave features? They surely do. Although macroscopic material particles display wave properties, the corresponding wavelengths are too small to detect; being very massive, macroscopic objects have extremely small wavelengths.
At the microscopic level, however, the waves associated with material particles are of the same size or exceed the size of the system. Microscopic particles therefore exhibit clearly noticeable wave-like aspects.
The general rule is: whenever the de Broglie wavelength of an object is in the range of, or exceeds, its size, the wave nature of the object is detectable and hence cannot be neglected.
But if its de Broglie wavelength is much too small compared to its size, the wave behaviour of this object is undetectable.
For a quantitative illustration of this general rule, let us calculate in the following example the wavelengths corresponding to two particles, one microscopic (electron) and the other macroscopic (ball).
Matter waves: According to De-Broglie, a wave is associated with each moving particle which is called matter waves.
That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p = h ν /c = h/λ, we can generalize this relation to any material particle with nonzero rest mass: each material particle of momentum 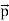 behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector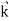 are governed by the speed and mass of the particle.
are governed by the speed and mass of the particle.
λ = |
Wave has wavelength λ here h is Planck's constant and p is the momentum of the moving particle.
We have seen that microscopic particles, such as electrons, display wave behaviour. What about macroscopic objects? Do they also display wave features? They surely do. Although macroscopic material particles display wave properties, the corresponding wavelengths are too small to detect; being very massive, macroscopic objects have extremely small wavelengths.
At the microscopic level, however, the waves associated with material particles are of the same size or exceed the size of the system. Microscopic particles therefore exhibit clearly noticeable wave-like aspects.
The general rule is: whenever the de Broglie wavelength of an object is in the range of, or exceeds, its size, the wave nature of the object is detectable and hence cannot be neglected.
But if its de Broglie wavelength is much too small compared to its size, the wave behaviour of this object is undetectable.
For a quantitative illustration of this general rule, let us calculate in the following example the wavelengths corresponding to two particles, one microscopic (electron) and the other macroscopic (ball).
De Broglie wavelength of matter waves: in terms of kinetic energy and associated with particle in thermal equilibrium
De-Broglie wavelength expressed in term of kinetic energy
If a particle has kinetic energy K.E., then
|
De-Broglie wavelength associated with particle in thermal equilibrium
If the particle is in thermal equilibrium at temperature T, then their kinetic energy is given by
|
Where K = 1.38 X 10-23 J/K
For an electron
m = 9.1X 10-31 Kg; e = 1.6 X 10-19 C; h = 6.62 X 10-34 J.s |
Therefore
|
Example: What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?
Solution:
(a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s) p = 4.92 × 10–24 kg m/s de Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s λ= 0.135 nm (b)For the ball: Mass m’ = 0.150 kg, Speed v ’= 30.0 m/s. Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s) p’= 4.50 kg m/s de Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m
|
The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement.
Example: What is the frequency of a photon with energy of 4.5 eV?
Solution:
E = (4.5 eV) x (1.60 x 10-19 J/eV) = 7.2 x 10-19 J E = hf h = 6.63 x 10-34 J x s |
Properties of matter waves
- Matter waves are the waves associated with matter in motion. Wavelength of the matter waves is given by λ=h/p.
- Matter waves are not progressive waves. They are localized waves.
- Matter waves are not single waves. They are group of waves (wave packet) assumed formed due to the superposition of two or more progressive waves.
- Matter waves called pilot waves and they represent the direction of propagation of matter.
- Unlike electromagnetic waves, matter waves will not have constant speed. The speed of matter waves depends on the mass of the particle.
- Vg x Vp=C2 shows that Vp, phase velocity of matter waves is greater than velocity of light. This shows that matter waves not physical waves
- Lighter the particle, greater is the De-Broglie wave length.
- The faster the particle moves, the smaller is its De-Broglie wave length.
- The De-Broglie wave length of a particle in independent of the charge or nature of the particle.
- The matter waves are not electromagnetic in nature. The electromagnetic waves are produced only by charged particle.
Key Takeaways
- Quantum mechanics began with two deceptively simple formula E=
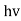 and p= h/λ. These are the Einstein and de Broglie relations respectively.
and p= h/λ. These are the Einstein and de Broglie relations respectively. - De Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
- All material particles should also display dual wave–particle behaviour. That is, the wave–particle duality present in light must also occur in matter.
- The expressions known as the de Broglie relation
- λ =
 =
=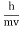
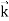 =
= 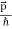
- Where ℏ = h/2π. The expression known as the de Broglie relation
- λ =
We know that in classical physics a particle is well localized in space. We can calculate its position and velocity simultaneously.
But for quantum mechanics, a particle is not well localized in space. We cannot calculate its position and velocity simultaneously.
In Quantum mechanics it is describe that the matter wave associated with the particle. Wave functions depend on the whole space. Hence, they cannot be localized.
If the wave function is made to vanish everywhere except in the neighbourhood of the particle or the neighbourhood of the classical trajectory, it can then be used to describe the dynamics of the particle. That is a particle which is localized within a certain region of space can be described by a matter wave whose amplitude is large in that region and zero outside it. This matter wave must then be localized around the region of space within which the particle is confined.
A localized wave function is called a Wave Packet or Wave Group. A wave packet or wave group therefore consists of a group of waves of slightly different wavelengths with phases and amplitudes so chosen that they interfere constructively over a small region of space and destructively elsewhere.
Wave packets are Not only useful in the explanation of isolated particles that are confined to a certain spatial region but they also play a key role in understanding the connection between quantum mechanics and classical mechanics. The wave packet concept also represents a uniting mathematical tool that describes particle-like behaviour and also its wave-like behaviour.
Phase and group velocity are two important and related concepts in wave mechanics. They arise in quantum mechanics in the time development of the state function for the continuous case, i.e. wave packets.
According to the theory of relativity particle velocity (v) is always less than the speed of light c. but according to the De-Broglie wave velocity must be greater than c. This is an unexpected result. According to this the de-Broglie wave associated with the particle would travel faster than the particle itself thus leaving the particle far behind.
The difficulty was recovered by Schrodinger. He proposed that a material particle in motion is equivalent to a wave packet rather than a single wave. Wave packet comprises of a group of waves, each with slightly different velocity and wavelength.
Such a wave packet moves with its own velocity vg called the group velocity.
The individual wave forming the wave packet possesses an average velocity vp called the phase velocity.
|
Figure 1: Wave Packet
It can be shown that the velocity of the material particle v is the same as group velocity
Let us assume two wave trains have same amplitude but different frequency and phase velocities u (x, t) =A sin(ωt - kx) …….(1) u’(x, t) =A sin[(ω+∆ω)t-(k+∆k)x] …….(2) Where ω and (ω+Δω) are angular frequencies and k and (k +Δk) are propagation constants The superposition of two waves is of the form ψ(x,t) = u +u’ = A sin(ωt - kx)sin[(ω+∆ω)t - (k+∆k)x] …….(3) As Δ ω and Δk are small therefore (ω+Δω) ψ(x,t) = 2Acos[ This equation represents a vibration of amplitude 2Acos[ The phase of the resultant wave moves with the velocity known as phase velocity vp= And the amplitude moves with the velocity known as group velocity vg = vg = |
Key Takeaways
- A localized wave function is called a Wave Packet or Wave Group. A wave packet or wave group therefore consists of a group of waves of slightly different wavelengths with phases and amplitudes so chosen that they interfere constructively over a small region of space and destructively elsewhere.
- Wave packet moves with its own velocity vg called the group velocity. vg =
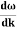
- The individual wave forming the wave packet possesses an average velocity vp called the phase velocity. vp=
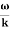
According to classical physics, given the initial conditions and the forces acting on a system, the future behaviour (unique path) of this physical system can be determined exactly. That is, if the initial coordinates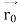 , velocity
, velocity 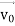 , and all the forces acting on the particle are known, the position
, and all the forces acting on the particle are known, the position 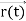 , and velocity
, and velocity 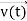 are uniquely determined by means of Newton’s second law. So, by Classical physics it can be easily derived.
are uniquely determined by means of Newton’s second law. So, by Classical physics it can be easily derived.
Does this hold for the microphysical world?
Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle.
In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
|
This principle indicates that, although it is possible to measure the momentum or position of a particle accurately, it is not possible to measure these two observables simultaneously to an arbitrary accuracy. That is, we cannot localize a microscopic particle without giving to it a rather large momentum.
We cannot measure the position without disturbing it; there is no way to carry out such a measurement passively as it is bound to change the momentum.
To understand this, consider measuring the position of a macroscopic object (you can consider a car) and the position of a microscopic system (you can consider an electron in an atom). On the one hand, to locate the position of a macroscopic object, you need simply to observe it; the light that strikes it and gets reflected to the detector (your eyes or a measuring device) can in no measurable way affect the motion of the object.
On the other hand, to measure the position of an electron in an atom, you must use radiation of very short wavelength (the size of the atom). The energy of this radiation is high enough to change tremendously the momentum of the electron; the mere observation of the electron affects its motion so much that it can knock it entirely out of its orbit.
It is therefore impossible to determine the position and the momentum simultaneously to arbitrary accuracy. If a particle were localized, its wave function would become zero everywhere else and its wave would then have a very short wavelength. According to de Broglie’s relation p = ℏ /λ,
Time Energy Uncertainty Relation
The momentum of this particle will be rather high. Formally, this means that if a particle is accurately localized (i.e., ∆x  0), there will be total uncertainty about its momentum (i.e., ∆px
0), there will be total uncertainty about its momentum (i.e., ∆px 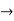 ∞).
∞).
Since all quantum phenomena are described by waves, we have no choice but to accept limits on our ability to measure simultaneously any two complementary variables.
Heisenberg’s uncertainty principle can be generalized to any pair of complementary, or canonically conjugate, dynamical variables: it is impossible to devise an experiment that can measure simultaneously two complementary variables to arbitrary accuracy. If this were ever achieved, the theory of quantum mechanics would collapse.
Energy and time, for instance, form a pair of complementary variables. Their simultaneous measurement must obey the time–energy uncertainty relation:
|
This relation states that if we make two measurements of the energy of a system and if these measurements are separated by a time interval ∆t, the measured energies will differ by an amount ∆E which can in no way be smaller than ℏ /∆t. If the time interval between the two measurements is large, the energy difference will be small. This can be attributed to the fact that, when the first measurement is carried out, the system becomes perturbed and it takes it a long time to return to its initial, unperturbed state. This expression is particularly useful in the study of decay processes, for it specifies the relationship between the mean lifetime and the energy width of the excited states.
In contrast to classical physics, quantum mechanics is a completely indeterministic theory. Asking about the position or momentum of an electron, one cannot get a definite answer; only a probabilistic answer is possible.
According to the uncertainty principle, if the position of a quantum system is well defined its momentum will be totally undefined.
APPLICATION OF UNCERTAINTY PRINCIPLE
The Heisenberg uncertainty principle based on quantum physics explains a number of facts which could not be explained by classical physics.
- Non-existence of electrons in the nucleus or Non-confinement of electron in the nucleus)
One of the applications is to prove that electron cannot exist inside the nucleus.
But to prove it, let us assume that electrons exist in the nucleus.
As the radius of the nucleus in approximately 10-14m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by
According to uncertainty principle
∆x ∆p =h/2π
Thus ∆p=h/2π∆x
Or ∆p=6.62 x10-34/2 x 3.14 x 10-14
Or ∆p=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron then the momentum of electron should be at least of this order that is p=1.05*10-20 kg m/sec.
An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formula
E = 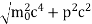
|
Therefore, if the electron exists in the nucleus, it should have an energy of the order of 19.6 MeV.
However, it is observed that beta-particles (electrons) ejected from the nucleus during b – decay have energies of approximately 3 Me V, which is quite different from the calculated value of 19.6 MeV.
Another reason that electron cannot exist inside the nucleus is that experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.
Therefore, it is confirmed that electrons do not exist inside the nucleus.
2. Ground State Energy of A Harmonic Oscillator or Calculation of zero point energy
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle. As well as atoms and molecules, the empty space of the vacuum has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions and force fields, whose quanta are bosons. All these fields have zero-point energy.
The minimum energy of a system at o k (zero kelvin) is called zero-point energy.
Consider a particle which is confined to move under the influence of potential of dimensions a. Since the particle may be present anywhere in these dimensions, so uncertainty in position
∆x = a/2 (half the diameter). |
According to uncertainty principle
∆x∆px = ℏ/2 |
or
Thus
∆px= ℏ /2∆x ∆px= ℏ /2a/2 = ℏ /a |
Uncertainty in momentum of particle along x-axis is
∆px= ℏ /a |
Assuming the momentum of particle to be at least equal to uncertainty in it, the lowest possible value of K.E. of particle is given by
K.E. = |
Where m is the mass of the particle.
Energy even at O K is given by the above equation. This minimum energy is called the zero-point energy.
This implies that even at zero kelvin, the particle is never at rest. If it is so, then ∆pX = 0, which is not possible. [It gives ∆x = ∞]
3. Existence of proton, neutron and alpha particles within the nucleus.
We know that the rest mass of the protons and neutron is of the order of
1.67x 10-27 kg. Hence, the value of momentum 5.27 x 10-21 kg.m/sec from calculation and also the value of v come out to be 3x 105m/sec.
The corresponding value of kinetic energy of a neutron or a proton is
E =
|
Since the rest mass of the a-particle is nearly four times the proton mass, therefore the alpha particle should have a minimum kinetic energy of one fourth of 52.05 keV, or about 13 keV. Since the energy carried by the protons or neutrons emitted by the nuclei are greater than 52 keV and for a-particle more than 13 keV, these particles can exist in the nuclei.
4. Size of Elementary cell in Phase space
We have studied in our previous class that state of a microsystem is defined by six variables – three are due to position and three due to momentum.
Hence, a system of N particles needs 6 N variables
If ∆ x and ∆px be the uncertainly in position and in momentum measurements then
∆ x ∆ px = |
Similarly
∆ y ∆ py = |
And
∆ z ∆ pz = |
Multiplying these three equations, we get
∆ x ∆ y ∆ z ∆ px ∆ py ∆ pz = ( |
The above product is called the volume of elementary cell in phase space.
So, volume of an elementary cell in phase space 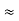 10-101 units, (for quantum statistics) being
10-101 units, (for quantum statistics) being 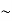
 .
.
5. Accurate limit of frequency of radiation emitted by an atom
Consider the radiation emitted from an excited atom. The energy of this atom will decrease when it emits one or more photons of characteristic frequency.
The average period between excitation of the atom and the release of energy is about 10-8 seconds.
Thus, uncertainly in energy is
∆ E |
Or
∆ E |
Or
∆ E |
Frequency of light is uncertain by
∆ ν = |
As a result, the radiation from an excited atom does not have the noted precise frequency new ν - ∆ ν and ν + ∆ ν.
Key Takeaways
- Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px).
- The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
|
3. This principle indicates that, although it is possible to measure the momentum or position of a particle accurately, it is not possible to measure these two observables simultaneously to an arbitrary accuracy. That is, we cannot localize a microscopic particle without giving to it a rather large momentum.
4. Energy and time, for instance, form a pair of complementary variables. Their simultaneous measurement must obey the time–energy uncertainty relation:
|
5. Electron cannot exist inside the nucleus because experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.
6. Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.
7. Heisenberg uncertainty principle proves proton, neutron and alpha particles exists within the nucleus.
8. Size of Elementary cell in Phase space is given by Heisenberg uncertainty principle
9. Frequency of light is uncertain by
10. ∆ ν = |
Quantum theory and determinism usually do not go together. A natural combination is quantum theory and randomness. Indeed, when in the end of 19th century physics seemed to be close to provide a very good deterministic explanation of all observed phenomena, Lord Kelvin identified “two clouds” on “the beauty and clear-ness of the dynamical theory”. One of this “clouds” was the quantum theory which brought a consensus that there is randomness in physics. Recently we even “certify” randomness using quantum experiments
The quantum theory of the wave function of the Universe is a very successful deterministic theory fully consistent with our experimental evidence. However, it requires accepting that the world we experience is only part of the reality and there are numerous parallel worlds. The existence of parallel worlds allows us to have a clear deterministic and local physical theory.
Wave Function
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as
ψ(x, y, z, t) = a + ib and its complex conjugate as ψ*(x, y, z, t) = a – ib. The product of wave function and its complex conjugate is ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2 a2 + b2 is a real quantity. |
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
- The wave function must be single valued at each point.
- The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.
- ψ must be finite everywhere.
- ψ must be continuous everywhere and
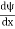 must also be continuous everywhere except where V(x) is infinite.
must also be continuous everywhere except where V(x) is infinite. - ψ (x) must vanish ψ
 0 as x
0 as x .
. - The wave function should satisfy the normalization condition. Normalization condition of a wave function ψ is mathematical statement of existence of the particle somewhere. so that if we sum up all possible values ∑|ψ(xi,t)|2∆xi we must obtain 1. The total probability of finding the particle anywhere must be one. Normalization condition is given as
|
Only wave function with all these properties can yield physically meaningful result.
Physical significance of wave function
- The wave function ‘Ѱ’ has no physical meaning. it is a complex quantity representing the variation of a matter wave.
- The wave function Ѱ(r,t) describes the position of particle with respect to time .
- It can be considered as ‘probability amplitude’ since it is used to find the location of the particle.
- The square of the wave function gives the probability density of the particle which is represented by the wave function itself.
- More the value of probability density, more likely to find the particle in that region.
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.
All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics.
Statistical Interpretation
It is not possible to measure all properties of a quantum system precisely. Max Born suggested that the wave function was related to the probability that an observable has a specific value.
In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2’. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’ . Thus Ψ2 is a measure of particle density.
According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dxdydz) is given by
|
Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space. i.e.
Or |
This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function.
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
Key Takeaways
- The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable.
- The wave function must be single valued at each point. The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1. ψ must be finite everywhere.
- According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dxdydz) is given by
|
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So We have
E= K+V = |
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk.
Using this equation (1) for the energy will become
ℏω = |
A wave with frequency ω and wave number k can be written as usual as
ψ(x, t) =Aei(kx−ωt) ……….. (3) |
the above equation is for one dimensional and for three dimensional we can write it as ψ(r, t) =Aei(k·r−ωt) ……….. (4) But here we will stick to one dimension only.
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain ℏ(ωψ) = This is the time-dependent Schrodinger equation. If we put the x and t in above equation then equation (7) takes the form as given below
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
We already know that E=
Eψ = -
This is called the time-independent Schrodinger equation.
|
Key Takeaways
- Schrodinger wave equation, is the fundamental equation of quantum mechanics
- The time-dependent Schrodinger equation is given by
|
3. The time-independent Schrodinger equation is given by
Eψ = - |
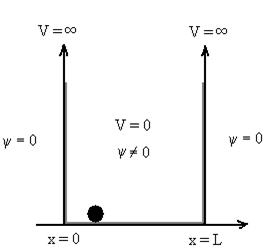
1.7.1 PARTICLE IN INFINITE POTENTIAL WELL
Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
The potential function is expressed as
V= 0 for 0 V= |
Figure 2: Particle in deep potential well |
The probability of finding the particle outside the well is zero (i.e. Ѱ =0)
Inside the well, the Schrödinger wave equation is written as
|
Substituting
writing the SWE for 1-D we get
The general equation of above equation may be expressed as ψ = Asin (kx + ϕ) …………….(5) Where A and ϕ are constants to be determined by boundary conditions Condition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5) 0 = Asin kL As A k = where n= 1,2,3,4……… Substituting the value of k from (7) to (3)
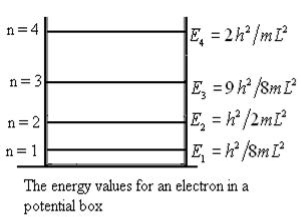
This gives energy of level En = It is clear that the energy values of the particle in well are discrete not continuous. |
Figure 3: The energy values for an electron in a potential box |
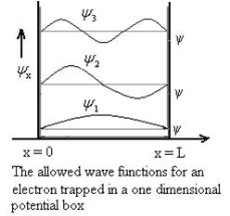
Using (6) and (7) equation (5) becomes, the corresponding wave functions will be ψ = ψn = Asin The probability density |ψ(x,t)|2 = ψ ψ* |ψ(x,t)|2 = A2sin2 The probability density is zero at x = 0 and x = L. since the particle is always within the well
A = Substituting A in equation (9) we get ψ = ψn = The above equation (12) is normalized wave function or Eigen function belonging to energy value En |
Figure 4: Wave function for Particle |
Key Takeaways
- It is assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
- The probability of finding the particle outside the well is zero (i.e. Ѱ =0)
- The energy values of the particle in well are discrete not continuous and Energy of level is given by
- En =
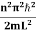 n=1,2,3,4…so on
n=1,2,3,4…so on - The probability density is given by
- |ψ(x,t)|2 = A2sin2
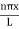
1.7.2 PARTICLE IN FINITE POTENTIAL WELL
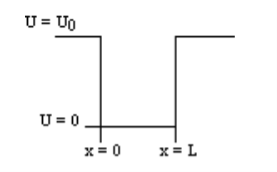
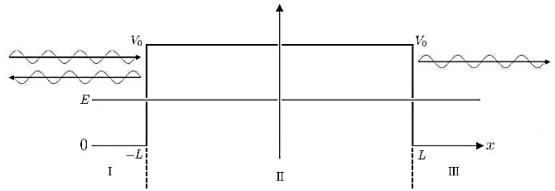
Consider the following piecewise continuous, finite potential energy: U=U0 x <0 (1) U= 0 0 U=U0 L < x. (3) We want to solve Schroedinger’s Equation for this potential to get the wave functions and allowed energies for E < U0. We will refer to the three regions as regions 0, 1, and 2 with associated wave functions ψ0,ψ1,ψ2.
Figure 5: Finite Square Well Potential Energy The time-invariant, non-relativistic Schroedinger’s equation is
that can be rearranged to give
It is convenient to define two new variables (both positive), one for regions 0 and 2, and one for region 1—they are wavenumbers:
and Schrödinger’s equation becomes
In regions 0 and 2 the general solution is a linear combination of exponentials with the same form, but with different constants, namely
In region 1 we have the same general solution that we had for the infinite square well,
Equations (10) to (12) have 7 unknowns—A,B,C,D,F,G and the energy E that is im-plicitly contained in the variables κ0,k1. Therefore we need to get 7 equations to be ableto solve for the unknowns. We will first use the requirement that the wavefunction remain finite everywhere. Consider ψ2 as x→∞. For this to remain finite we must require G= 0. Similarly, as x→−∞, we require A= 0. Our solutions become
The next step is to require that the wavefunction and its first derivative be continuous everywhere, and in our case we look at the boundaries, x= 0 and x=L.
Hence ψ0=D exp(+κ0x).Take derivatives of the wave functions,
|
|
There remain 3 unknowns, D,F, and E. Finding them is a bit messier! Consider the boundary conditions at x=L,
|
We are not going much farther, but if we divided Equation (22) by Equation (23), we can see that the constants D and F cancel leaving us with one rather difficult equation to solve for energy E (remember this is implicitly included in the values of k1and κ0.)
There is one remaining condition, normalization, that for this problem is
|
Even without solving the entire problem we can make some conclusions about the wave-function and the allowed energy levels. Recall that for an infinite square well potential of width L the allowed energies are quantized and
|
Here is Equation (22)/ Equation (23)
|
Now put in the values ofκ0andk1from Equations (6) and (7) and do some algebra to get
|
This equation is a single equation in a single unknown, E < U0. Once we have the details of our particle (its mass) and the potential energy (depth U0 and width L), we can solve it. There is no analytic solution, only a numerical one.
From equation (25) With n being any positive integer. Outside the well the wavefunction is 0. We are certain that the particle is somewhere inside the box, so ∆x ∞ =L.
With the finite well, the wavefunction is not zero outside the well,
Figure 6: Wave function in Finite well
|
So ∆x finite> L, hence from the uncertainty principle, ∆pfinite x<∆p∞x. This suggests that the average value of momentum is less for the finite well, and therefore that the kinetic energy inside the well is less for the finite well than for the infinite well. Indeed this is borne out with detailed analysis. In addition, the number of allowed energy levels is finite, and there is a possibility that a well may be sufficiently narrow or sufficiently shallow that no energy levels are allowed. Also note that the non-zero wave functions in regions 0 and 2 mean that there is a non-zero probability of finding the particle in a region that is classically forbidden, a region where the total energy is less than the potential energy so that the kinetic energy is negative.
Key Takeaways
- The average value of momentum is less for the finite well, and therefore that the kinetic energy inside the well is less for the finite well than for the infinite well.
- In addition, the number of allowed energy levels is finite, and there is a possibility that a well may be sufficiently narrow or sufficiently shallow that no energy levels are allowed.
- Also note that the non-zero wave functions in regions 0 and 2 mean that there is a non-zero probability of finding the particle in a region that is classically forbidden, a region where the total energy is less than the potential energy so that the kinetic energy is negative.
The so-called tunnel effect of quantum mechanics can be derived from a special case of the potential well, by changing −V0 into +V0, thus creating a potential barrier, as seen in Figure.
|
|
Figure 7: Tunnel effect
For a given potential barrier with height V0 the solutions of the Schrodinger equation with energy E < V0 still have a non-vanishing probability density in region III, which allows them to “tunnel” through the barrier although this would classically be forbidden.
Classically, a particle with less energy than the potential barrier could only be reflected. But in quantum mechanics, due to continuity the wave function decreases exponentially in the forbidden region II, resulting in a non-vanishing probability density in region III.
It allows the particle to pass the barrier as if it was through a tunnel, this linguistic illustration gives rise to the name tunnel effect.
Mathematically, we can use the solutions
|
Where
|
Since the exponent of the solution in region II is not imaginary anymore, So we have solution in the form their hyperbolic counterparts
Tunnelling – Transmission Coefficient
For the transmission amplitude we get the result
which, using the identity
gives the transmission coefficient
It can be simplified under the condition that q
and we can rewrite Equation (5) as
We then use Equation (2) to express the transmission coefficient by the energy and potential strength to get
Using exey=ex+y we can write the whole coefficient as an exponential function
Since we required that qL be much bigger than one and the logarithm increases only very slowly we can conclude that the first term in the exponent outweighs the second one, which we therefore neglect to obtain.
We now have a good approximation for the transmission probability of a single potential step, constant in certain interval and vanishing outside. This potential is of course
|
Figure 8: Calculation of Gamow factor: The generalization of the transmission |
coefficient, from a single constant potential barrier with width 2L, to the incorporation of a function V(x) is done straightforward by integration of infinitesimal potential barriers.
a very crude approximation of real life potentials, which usually are more complicated functions of x. To meet these concerns we can generalize the transmission coefficient of Equation (10) to the so called Gamow factor by “chopping” a given potential in infinitesimal potential steps with constant values and integrating over a reasonable range [x1,x2]for which the potential stays above a certain value, see Figure 8.
|
Physical Examples of Tunnelling
We will now briefly present some examples, where the tunnel effect explains the observed phenomena.
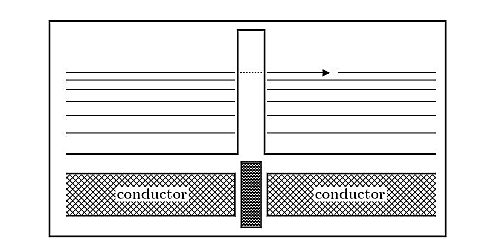
Tunnelling between conductors:
Imagine two conducting materials, separated by a thin insulating material, sketched in Figure 9. The tunnel effect then allows the electrons to tunnel through that barrier, thus creating a current. This effect is also observed for super conducting materials, where it is named Josephson effect.
Cold emission:
Electrons can be emitted from metals at very low temperatures, even without incident light if an exterior electric field is applied. Assuming that the electrons have a very low energy compared to the potential height, it is not very probable that an electron can tunnel through the potential barrier. Only if an electric field raises the energy of the electron, the transmission coefficient increases and the electron emission can be observed.
Figure 9: Tunnelling through insulator: Between two conducting materials, separated by a thin insulating barrier, the tunnel effect creates a current.
|
Key Takeaways
- In quantum mechanics, due to continuity the wave function decreases exponentially in the forbidden region II, resulting in a non-vanishing probability density in region III. It allows the particle to pass the barrier as if it was through a tunnel, this linguistic illustration gives rise to the name tunnel effect.
- The tunnel effect then allows the electrons to tunnel through that barrier, thus creating a current.
- This effect is also observed for super conducting materials, where it is named Josephson effect.
Reference
- Introduction to Solid State Physics -- Charles Kittel
- Solid State Physics-S 0 Pillai, 8th Ed New Age International Publishers-2018.
- Engineering physics- Gaur and Gupta, & S.Chand Publication
- Engineering physics - Avadhanalu and Kshirsagar, S.Chand Publication
- Semiconductor Device Fundamentals by Robert F. Pierret