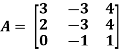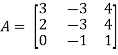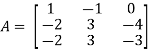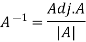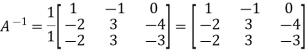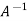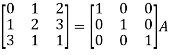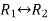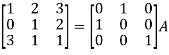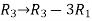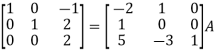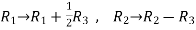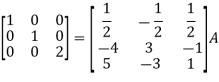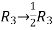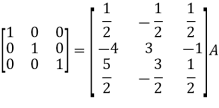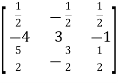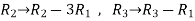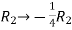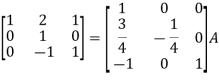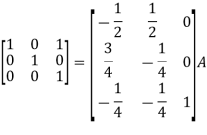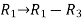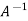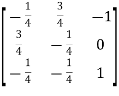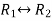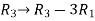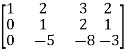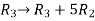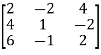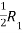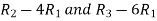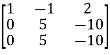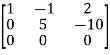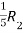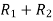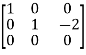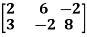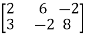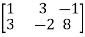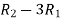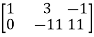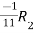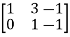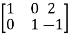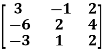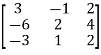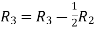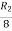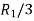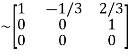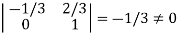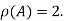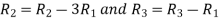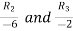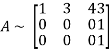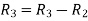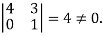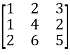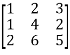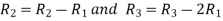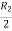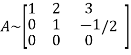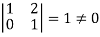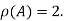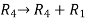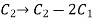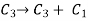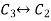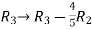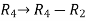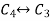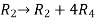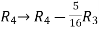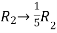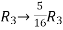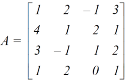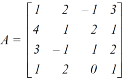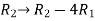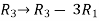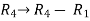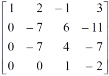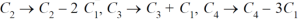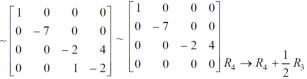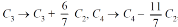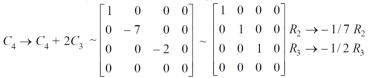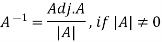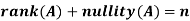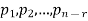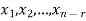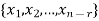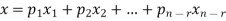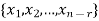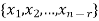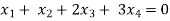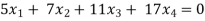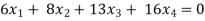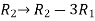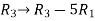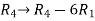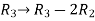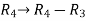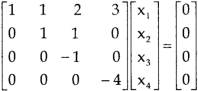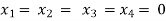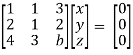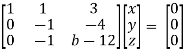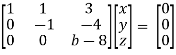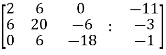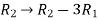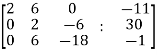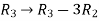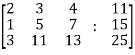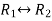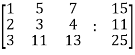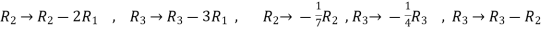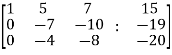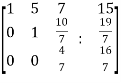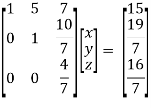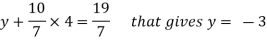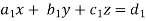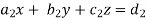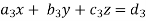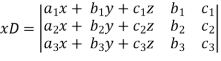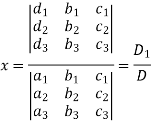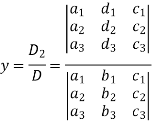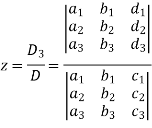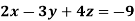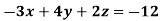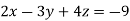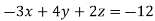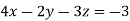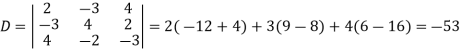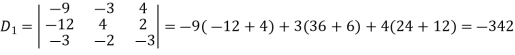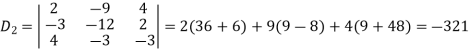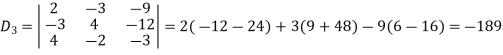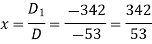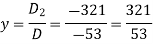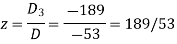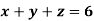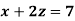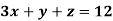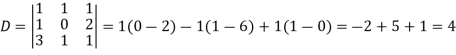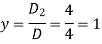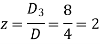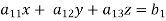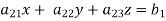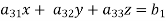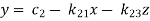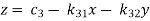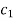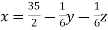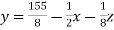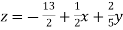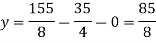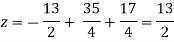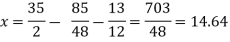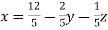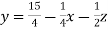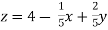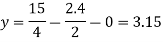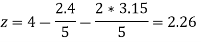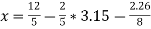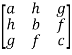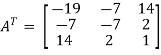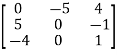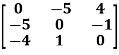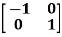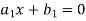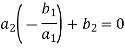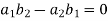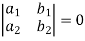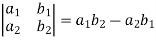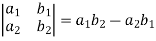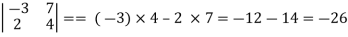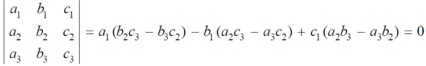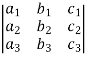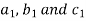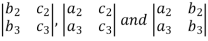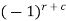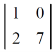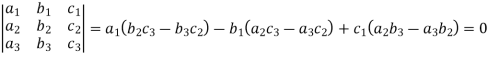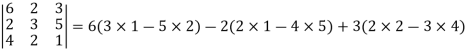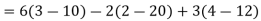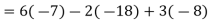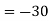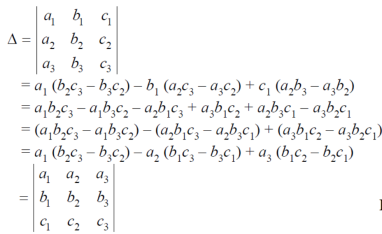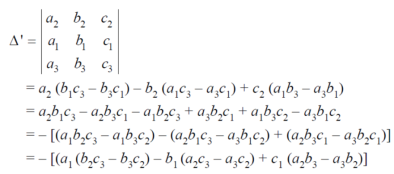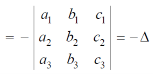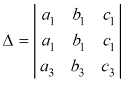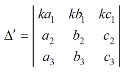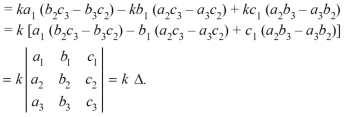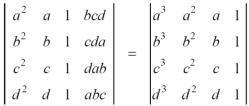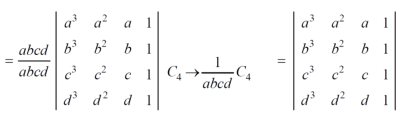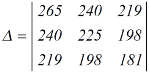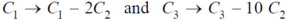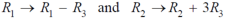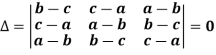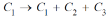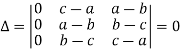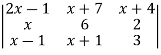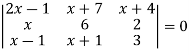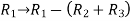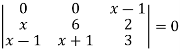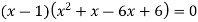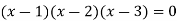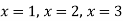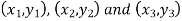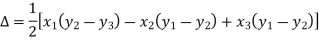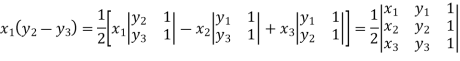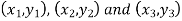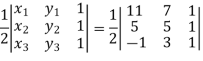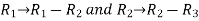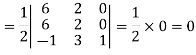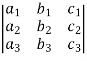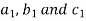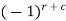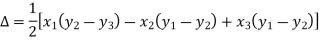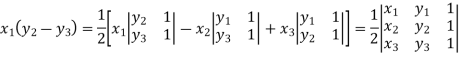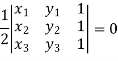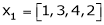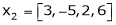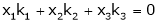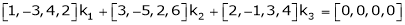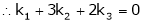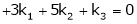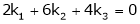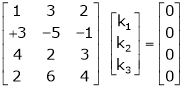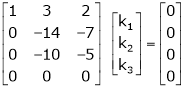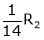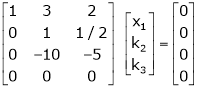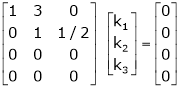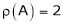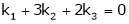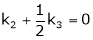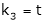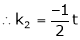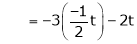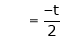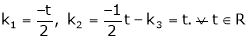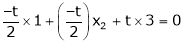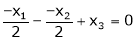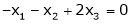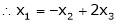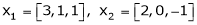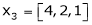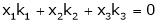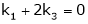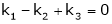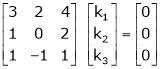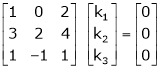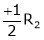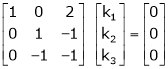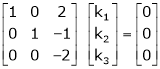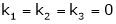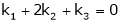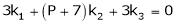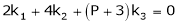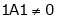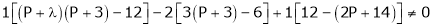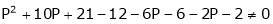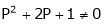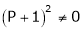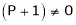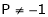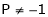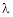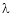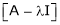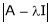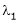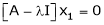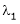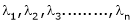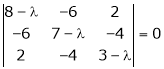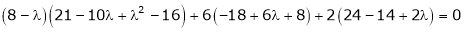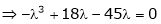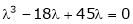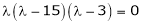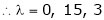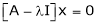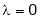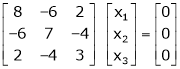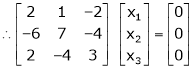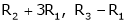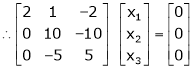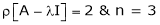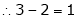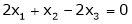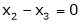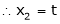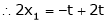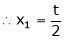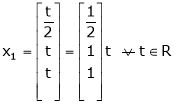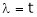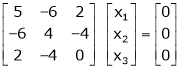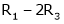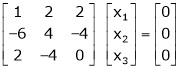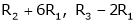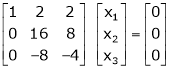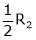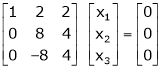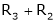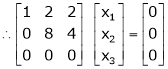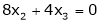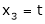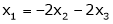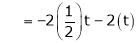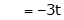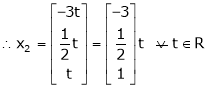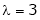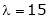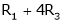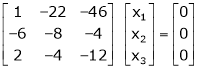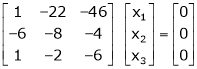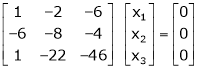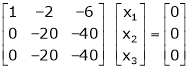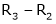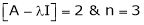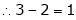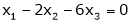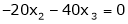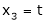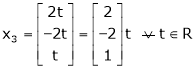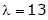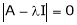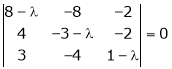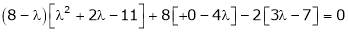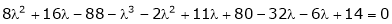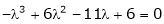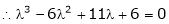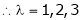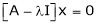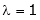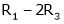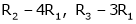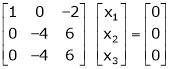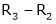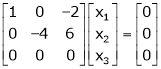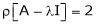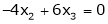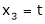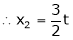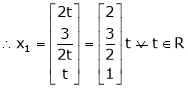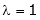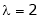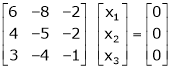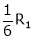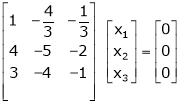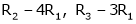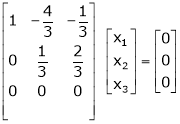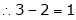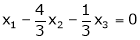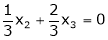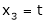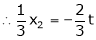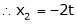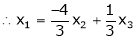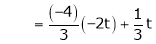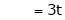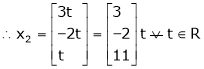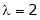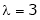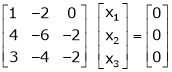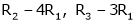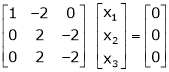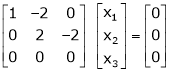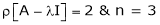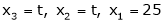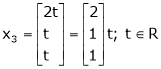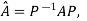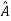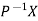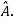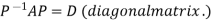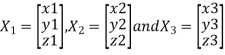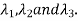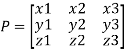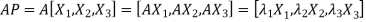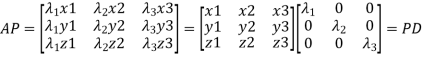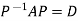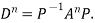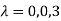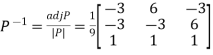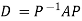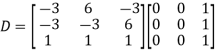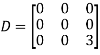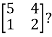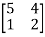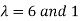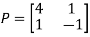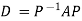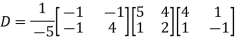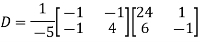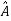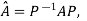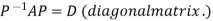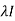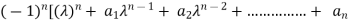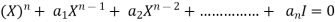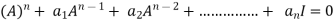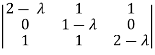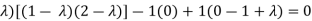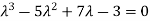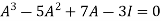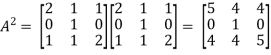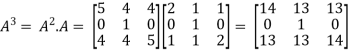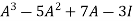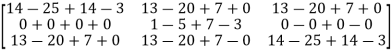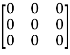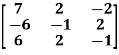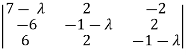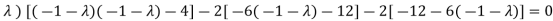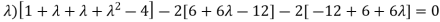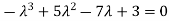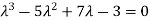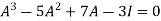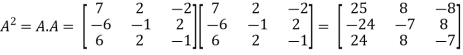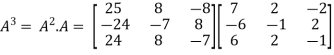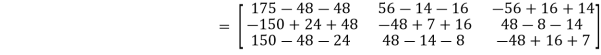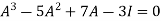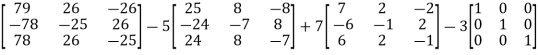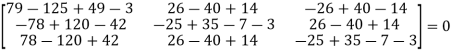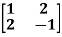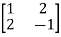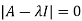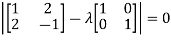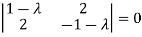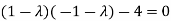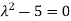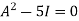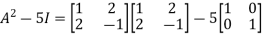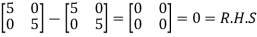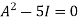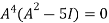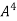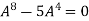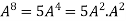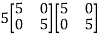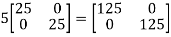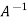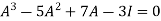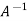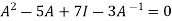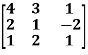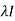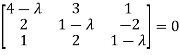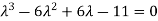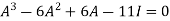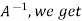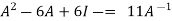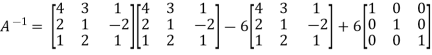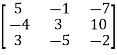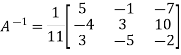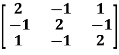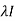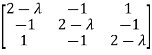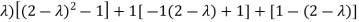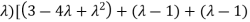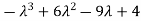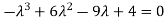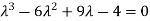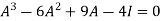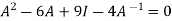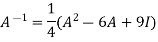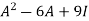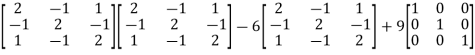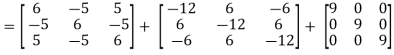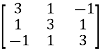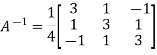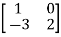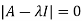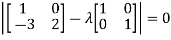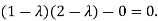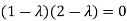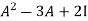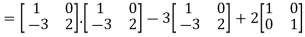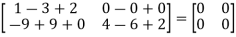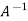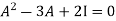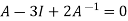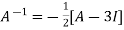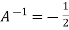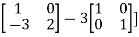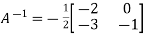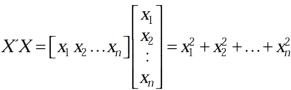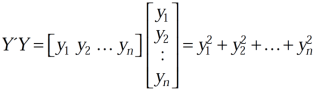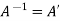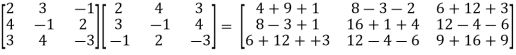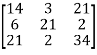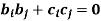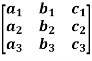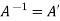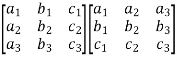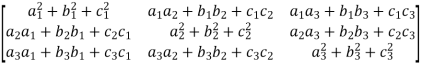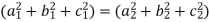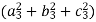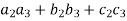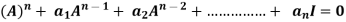UNIT-4
Linear algebra
Inverse of a matrix- The inverse of a matrix ‘A’ can be find as-
Example: Find the inverse of matrix ‘A’ if-
Sol. Here we have-
And the matrix formed by its co-factors of |A| is-
And
Therefore- We know that-
Inverse of a matrix by using elementary transformation- The following transformation are defined as elementary transformations- 1. Interchange of any two rows (column) 2. Multiplication of any row or column by any non-zero scalar quantity k. 3. Addition to one row (column) of another row(column) multiplied by any non-zero scalar. The symbol ~ is used for equivalence. Elementary matrices- If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix. Note- Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.
The method of finding inverse of a non-singular matrix by using elementary transformation- Working steps- 1. Write A = IA 2. Perform elementary row transformation of A of the left side and I on right side. 3. Apply elementary row transformation until ‘A’ (left side) reduces to I, then I reduces to
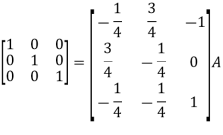
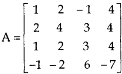
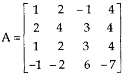
Example-1: Find the inverse of matrix ‘A’ by using elementary transformation- A = Sol. Write the matrix ‘A’ as- A = IA
Apply
Apply
Apply
Apply
Apply
So that,
Example-2: Find the inverse of matrix ‘A’ by using elementary transformation- A = Sol. Write the matrix ‘A’ as- A = IA
Apply
Apply
Apply
Apply
So that
Rank of a matrix- Rank of a matrix by echelon form- The rank of a matrix (r) can be defined as – 1. It has at least one non-zero minor of order r. 2. Every minor of A of order higher than r is zero. Example: Find the rank of a matrix M by echelon form. M =
Sol. First we will convert the matrix M into echelon form, M = Apply, M = Apply M =
Apply M = We can see that, in this echelon form of matrix, the number of non – zero rows is 3. So that the rank of matrix X will be 3.
Example: Find the rank of a matrix A by echelon form. A = Sol. Convert the matrix A into echelon form, A = Apply A = Apply A = Apply A = Apply A = Apply A = Therefore, the rank of the matrix will be 2.
Example: Find the rank of a matrix A by echelon form. A = Sol. Transform the matrix A into echelon form, then find the rank, We have, A = Apply, A = Apply A = Apply A = Apply A = Hence the rank of the matrix will be 2.
Example: Find the rank of the following matrices by echelon form? Let A = Applying A Applying A Applying A Applying A It is clear that minor of order 3 vanishes but minor of order 2 exists as Hence rank of a given matrix A is 2 denoted by
2. let A = Applying
Applying
Applying
The minor of order 3 vanishes but minor of order 2 non zero as Hence the rank of matrix A is 2 denoted by
3. Let A =
Apply
Apply
Apply
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as Hence the rank of given matrix is 2 i.e.
Rank of a matrix by normal form- Any matrix ‘A’ which is non-zero can be reduced to a normal form of ‘A’ by using elementary transformations. There are 4 types of normal forms –
The number r obtained is known as rank of matrix A. Both row and column transformations may be used in order to find the rank of the matrix.
Note-Normal form is also known as canonical form
Example: reduce the matrix A to its normal form and find rank as well.
Sol. We have,
We will apply elementary row operation,
We get,
Now apply column transformation,
We get,
Apply
Apply
Apply
Apply
Apply
As we can see this is required normal form of matrix A. Therefore, the rank of matrix A is 3.
Example: Find the rank of a matrix A by reducing into its normal form.
Sol. We are given,
Apply
Apply
This is the normal form of matrix A. So that the rank of matrix A = 3 |
Key takeaways
Inverse of a matrix-
2. Normal form is also known as canonical form
|
Let A is a matrix of order m by n, then-
Proof: If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix. So that in this case null-space (A) = {0}, so nullity (A) = 0. Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0. Let Here Moreover every solution is to Ax = 0 is a linear combination of
Which shows that Thus |
There are two types of linear equations- 1. Consistent 2. Inconsistent Let’s understand about these two types of linear equations.
Consistent – If a system of equations has one or more than one solution, it is said be consistent. There could be unique solution or infinite solution. For example- A system of linear equations- 2x + 4y = 9 x + y = 5 Has unique solution, Whereas, A system of linear equations- 2x + y = 6 4x + 2y = 12 Has infinite solutions. Inconsistent- If a system of equations has no solution, then it is called inconsistent.
Consistency of a system of linear equations- Suppose that a system of linear equations is given as-
This is the format as AX = B Its augmented matrix is- [A:B] = C (1) Consistent equations- If Rank of A = Rank of C Here, Rank of A = Rank of C = n ( no. of unknown) – unique solution And Rank of A = Rank of C = r , where r<n - infinite solutions (2) Inconsistent equations- If Rank of A ≠ Rank of C
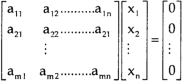
Solution of homogeneous system of linear equations- A system of linear equations of the form AX = O is said to be homogeneous, where A denotes the coefficients and of matrix and O denotes the null vector. Suppose the system of homogeneous linear equations is,
It means , AX = O Which can be written in the form of matrix as below,
Note- A system of homogeneous linear equations always has a solution if 1. r(A) = n then there will be trivial solution, where n is the number of unknown, 2. r(A) < n , then there will be an infinite number of solution.
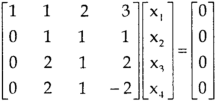
Example: Find the solution of the following homogeneous system of linear equations,
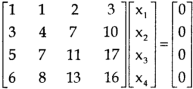
Sol. The given system of linear equations can be written in the form of matrix as follows,
Apply the elementary row transformation,
Here r(A) = 4, so that it has trivial solution,
Example: Find out the value of ‘b’ in the system of homogenenous equations- 2x + y + 2z = 0 x + y + 3z = 0 4x + 3y + bz = 0 Which has (1) Trivial solution (2) Non-trivial solution
Sol. (1) For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value. Now for non-trivial solution- (2) Convert the system of equations into matrix form- AX = O
Apply
For non-trivial solutions, r(A) = 2 < n b – 8 = 0 b = 8
Solution of non-homogeneous system of linear equations- Example-1: check whether the following system of linear equations is consistent of not. 2x + 6y = -11 6x + 20y – 6z = -3 6y – 18z = -1
Sol. Write the above system of linear equations in augmented matrix form,
Apply
Apply
Here the rank of C is 3 and the rank of A is 2 Therefore, both ranks are not equal. So that the given system of linear equations is not consistent.
Example: Check the consistency and find the values of x , y and z of the following system of linear equations. 2x + 3y + 4z = 11 X + 5y + 7z = 15 3x + 11y + 13z = 25
Sol. Re-write the system of equations in augmented matrix form. C = [A,B] That will be,
Apply
Now apply, We get,
Here rank of A = 3 And rank of C = 3, so that the system of equations is consistent, So that we can can solve the equations as below,
That gives, x + 5y + 7z = 15 ……………..(1) y + 10z/7 = 19/7 ………………(2) 4z/7 = 16/7 ………………….(3) From eq. (3) z = 4, From 2,
From eq.(1), we get x + 5(-3) + 7(4) = 15 That gives, x = 2 Therefore the values of x , y , z are 2 , -3 , 4 respectively.
Cramer’s rule- This method was introduced by Gabriel Cramer (1704 – 1752). Suppose we have to solve the following equations,
Now, let-
Multiply the second column by y and 3rd column by z and adding to the first column then we have-
Similarly we get-
And
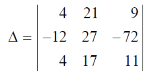
Example: Solve the following equations by using Cramer’s rule-
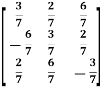
Sol. Here we have-
And here-
Now by using cramer’s rule-
Example: Solve the following system of linear equations-
Sol.
By using cramer’s rule-
Gauss-Seidel iteration method- Step by step method to solve the system of linear equation by using Gauss Seidal Iteration method- Suppose,
This system can be written as after dividing it by suitable constants,
Step-1 Here put y = 0 and z = 0 and x =
Then in second equation we put this value of x that we get the value of y. In the third eq. we get z by using the values of x and y Step-2: we repeat the same procedure
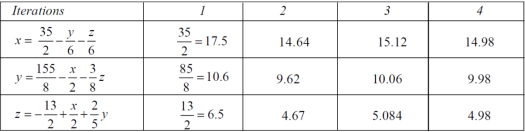
Example: solve the following system of linear equations by using Guassseidel method- 6x + y + z = 105 4x + 8y + 3z = 155 5x + 4y - 10z = 65
Sol. The above equations can be written as,
Now put z = y = 0 in first eq. We get x = 35/2 put x = 35/2 and z = 0 in eq. (2) we have,
Put the values of x and y in eq. 3
Again start from eq.(1) By putting the values of y and z y = 85/8 and z = 13/2 We get
The process can be showed in the table format as below
At the fourth iteration, we get the values of x = 14.98 , y = 9.98 , z = 4.98 Which are approximately equal to the actual values As x = 15 , y = 10 and y = 5 ( which are the actual values)
Example: Solve the following system of linear equations by using Guassseidel method- 5x + 2y + z = 12 x + 4y + 2z = 15 x + 2y + 5z = 20
sol. These equations can be written as ,
Put y and z equals to 0 in eq. 1 We get, x = 2.4 put x = 2.4, and z = 0 in eq. 2 , we get
Put x = 2.4 and y = 3.15 in eq.(3) , we get
Again start from eq.(1), put the values of y and z , we get
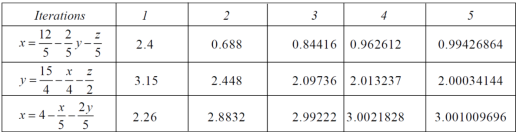
We repeat the process again and again , The following table can be obtained –
We see that the values are approx. equal to exact values. Exact values are, x = 1, y = 2, z = 3. |
Key takeaways
- A system of homogeneous linear equations always has a solution if
- r(A) = n then there will be trivial solution, where n is the number of unknown,
- r(A) < n , then there will be an infinite number of solution.
Symmetric matrix: Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself. For example:
Example: check whether the following matrix A is symmetric or not? A =
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix. So that, first we will find its transpose, Transpose of matrix A ,
Here, A = So that, the matrix A is symmetric.
Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix. Sol. Suppose A is any square matrix. Then, A = Now, (A + A’)’ = A’ + A A+A’ is a symmetric matrix. Also, (A - A’)’ = A’ – A Here A’ – A is an anti – symmetric matrix So that, Square matrix = symmetric matrix + anti-symmetric matrix
Skew-symmetric matrix- A square matrix A is said to be skew symmetrix matrix if – 1. A’ = -A, [ A’ is the transpose of A] 2. All the main diagonal elements will always be zero. For example- A = This is skew symmetric matrix, because transpose of matrix A is equals to negative A.
Example: check whether the following matrix A is symmetric or not? A = Sol. This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A. -A = A’
Orthogonal matrix- Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix. Such that, A. A’ = I Matrix × transpose of matrix = identity matrix Note- if |A| = 1, then we can say that matrix A is proper. Examples: |
Look at the following procedure in order to understand the concept of determinants- Let’s consider the two linear equations,
From first eq. , we get,
Put this value in second equation, we get
This can be written as,
The expansion of the determinant is given as,
Example: expand the determinant
Sol. As we know, expansion of the determinant is given by,
Then we get,
Now suppose we have three equations as below, where a, y and z are unknown,
Then the determinant will be of third order and can be defined as follows,
Minor – The minor of an element is define as determinant obtained by deleting the row and column containing the element. In a determinant,
The minor of
Cofactor – Cofactors can be defined as follows, Cofactor = Where r is the number of rows and c is the number of columns.
Example: Find the minors and cofactors of the first row of the determinant.
Sol. (1) The minor of element 2 will be, Delete the corresponding row and column of element 2, We get,
Which is equivalent to, 1 × 7 - 0 × 2 = 7 – 0 = 7
Similarly the minor of element 3 will be, 4× 7 - 0× 6 = 28 – 0 = 28
Minor of element 5, 4 × 2 - 1× 6 = 8 – 6 = 2 The cofactors of 2, 3 and 5 will be,
Example: expand the determinant:
Sol. As we know
Then,
Properties of determinants- (1) If the rows are interchanged into columns or columns into rows then the value of determinants does not change. Let us consider the following determinant:
(2) The sign of the value of determinant changes when two rows or two columns are interchanged. Interchange the first two rows of the following, we get
(3) If two rows or two columns are identical the the value of determinant will be zero. Let, the determinant has first two identical rows,
As we know that if we interchange the first two rows then the sign of the value of the determinant will be changed , so that
Hence proved (4) if the element of any row of a determinant be each multiplied by the same number then the determinant multiplied by the same number,
Example: prove the following without expanding the determinant.
Sol. Here in order to prove the above result, we follow the steps below,
hence proved.
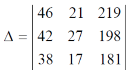
Example: prove that (without expanding) the determinant given below is equal zero.
Sol. Applying the operation,
We get,
Now applying the operation,
We get,
Apply,
We get,
Here first and second row are identical then we know that by property it becomes zero.
Example: Show that,
Sol. Applying
We get,
Example: Solve-
Sol: given-
Apply-
We get-
Applications of determinants- Determinants have various applications such as finding the area and condition of collinearity. Area of triangles- Suppose the three vertices of a triangle are
This is how we can find the area of the triangle.
Condition of collinearity- Let there are three points Then these three points will be collinear if -
Example: Show that the points given below are collinear-
Sol. First we need to find the area of these points and if the area is zero then we can say that these are collinear points- So that- We know that area enclosed by three points-
Apply-
So that these points are collinear. |
Key takeaways-
The minor of
3. Cofactor – Cofactors can be defined as follows, Cofactor = Where r is the number of rows and c is the number of columns. 4. Area of triangles-
5. Condition of collinearity-
|
First we will go through some important definitions before studying Eigen values and Eigen vectors. 1. Vector- An ordered n – touple of numbers is called an n – vector. Thus the ‘n’ numbers x1, x2, …………xn taken in order denote the vector x. i.e. x = (x1, x2, ……., xn). Where the numbers x1, x2, ………..,xn are called component or co – ordinates of a vector x. A vector may be written as row vector or a column vector. If A be an mxn matrix then each row will be an n – vector & each column will be an m – vector. 2. Linear dependence- A set of n – vectors. x1, x2, …….., xr is said to be linearly dependent if there exist scalars. k1, k2, …….,kr not all zero such that k1 + x2k2 + …………….. + xrkr = 0 … (1) 3. Linear independence- A set of r vectors x1, x2, ………….,xr is said to be linearly independent if there exist scalars k1, k2, …………, kr all zero such that x1 k1 + x2 k2 + …….. + xrkr = 0 Important notes-
k1 = k2 = …….=kr = 0. Then the vector x1, x2, ……,xr are said to linearly independent. 4. Linear combination- A vector x can be written in the form. x = x1 k1 + x2 k2 + ……….+xrkr where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr. Results:
Example 1 Are the vectors Solution: Consider a vector equation,
i.e.
Which can be written in matrix form as,
Here
Put
Thus i.e. i.e.
Since F11k2, k3 not all zero. Hence Example 2 Examine whether the following vectors are linearly independent or not.
Solution: Consider the vector equation,
i.e.
Which can be written in matrix form as,
R12
R2 – 3R1, R3 – R1
R3 + R2
Here Rank of coefficient matrix is equal to the no. of unknowns. i.e. r = n = 3. Hence the system has unique trivial solution. i.e. i.e. vector equation (1) has only trivial solution. Hence the given vectors x1, x2, x3 are linearly independent. Example 3 At what value of P the following vectors are linearly independent.
Solution: Consider the vector equation.
i.e.
This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution. If and only if Determinant of coefficient matrix is non zero.
i.e.
Thus for Note: If the rank of the coefficient matrix is r, it contains r linearly independent variables & the remaining vectors (if any) can be expressed as linear combination of these vectors. Characteristic equation: Let A he a square matrix, Note: Let a be a square matrix and ‘ 1) 2) The roots of a characteristic equations are known as characteristic root or latent roots, Eigen values or proper values of a matrix A.
Eigen vector: Suppose
Such a vector ‘x1’ is called as Eigen vector corresponding to the Eigen value
Properties of Eigen values:
Properties of Eigen vector:
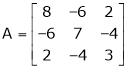
Example-1: Determine the Eigen values of Eigen vector of the matrix.
Solution: Consider the characteristic equation as, i.e. i.e.
i.e. Which is the required characteristic equation.
Now consider the equation
Case I: If
R1 + R2
Thus
Now rewrite equation as,
Put x3 = t
Thus Is the eigen vector corresponding to Case II: If
Here
Now rewrite the equations as,
Put
Is the eigen vector corresponding to Case III: If
Here rank of
Now rewrite the equations as,
Put
Thus Is the eigen vector for
Example 2 Find the Eigen values of Eigen vector for the matrix.
Solution: Consider the characteristic equation as i.e.
i.e.
Now consider the equation
Case I:
Thus
Now rewrite the equations as,
Put
I.e. the Eigen vector for Case II: If
Thus
Independent variables. Now rewrite the equations as,
Put
Is the Eigen vector for Now Case III: If
R1 – R2
Thus
Independent variables Now
Put Thus
Is the Eigen vector for |
Two square matrix
Such transformation of the matrix A into Similar matrices have the same Eigen values. If X is an Eigen vector of matrix A then Reduction to Diagonal Form: Let A be a square matrix of order n has n linearly independent Eigen vectors Which form the matrix P such that
Where P is called the modal matrix and D is known as spectral matrix. Procedure: let A be a square matrix of order 3. Let three Eigen vectors of A are Let
Or Or Note: The method of diagonalization is helpful in calculating power of a matrix.
We are using the example of 1.6* Example1: Diagonalise the matrix Let A= The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values
Then Also we know that
Example2: Diagonalise the matrix Let A = The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values Then Also we know that
|
Key takeaways
2. Let A be a square matrix of order n has n linearly independent Eigen vectors Which form the matrix P such that
Where P is called the modal matrix and D is known as spectral matrix. |
Statement- Every square matrix satisfies its characteristic equation , that means for every square matrix of order n, |A - Then the matrix equation-
Is satisfied by X = A That means
Example-1: Find the characteristic equation of the matrix A =
Sol. Characteristic equation of the matrix, we can be find as follows-
Which is, ( 2 -
According to cayley-Hamilton theorem,
Now we will verify equation (1),
Put the required values in equation (1) , we get
Hence the cayley-Hamilton theorem is verified.
Example-2: Find the characteristic equation of the the matrix A and verify Cayley-Hamilton theorem as well. A =
Sol. Characteristic equation will be-
( 7 - (7- (7- Which gives,
Or
According to cayley-Hamilton theorem,
In order to verify cayley-Hamilton theorem , we will find the values of So that,
Now
Put these values in equation(1), we get
Hence the cayley-hamilton theorem is verified.
Example-3:Using Cayley-Hamilton theorem, find
Sol. Let A = The characteristics equation of A is
Or Or By Cayley-Hamilton theorem L.H.S. = By Cayley-Hamilton theorem we have Multiply both side by
Or = =
Inverse of a matrix by Cayley-Hamilton theorem- We can find the inverse of any matrix by multiplying the characteristic equation With For example, suppose we have a characteristic equation
Then we can find
Example-1: Find the inverse of matrix A by using Cayley-Hamilton theorem. A =
Sol. The characteristic equation will be, |A -
Which gives, (4-
According to Cayley-Hamilton theorem,
Multiplying by
That means
On solving, 11 = = So that,
Example-2: Find the inverse of matrix A by using Cayley-Hamilton theorem. A =
Sol. The characteristic equation will be, |A - = = (2- = (2 - = That is,
Or
We know that by Cayley-Hamilton theorem,
Multiply equation(1) by
Or
Now we will find =
= Hence the inverse of matrix A is,
Example-3: Verify the Cayley-Hamilton theorem and find the inverse.
Sol. Let A = The characteristics equation of A is
Or Or Or By Cayley-Hamilton theorem L.H.S:
= Multiply both side by
Or Or Or
Orthogonal transformation- When a transformation from one set of rectangular coordinates to another set of rectangular coordinates , then this is called ‘orthogonal tranformation’. In other words- A linear transformation Y = AX is said to be orthogonal , if matrix A is orthogonal that means, AA’ = I = A’A We have,
And similarly,
If Y = AX is an orthogonal transformation , then we have X’X = Y’Y = (AX)’AX = X’A’ AX = X’(A’A)X Which is only possible , if A’A = I = AA’ and Therefore the square matrix A is said to be orthogonal if AA’ = A’A and
Example: Check whether the matrix A is orthogonal or not? A = Sol. To check the orthogonality of this matrix , first we need to find AA’ So that, AA’ =
= Here AA’ ≠ I So , we can say that matrix A is not an orthogonal matrix. Example: If the matrix A defines an orthogonal transformation , then show that
Where A =
Sol. As we know that an orthogonal matrix A , AA’ = I = A’A and We will find AA’, AA’ =
A will be orthogonal only if - AA’ = I In that case, it is only possible when,
And, (
NOTES- 1. The inverse and transpose of an orthogonal matrix is also orthogonal. 2. A linear transformation preserves length if and only if its matris is orthogonal. 3. The product of two or more than two orthogonal matrices is also orthogonal. 4. The determinant of an orthogonal matrix will always be ±1. |
Key takeaways
When a transformation from one set of rectangular coordinates to another set of rectangular coordinates , then this is called ‘orthogonal tranformation’. |
References
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass