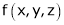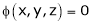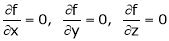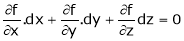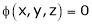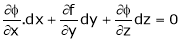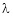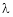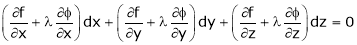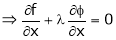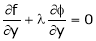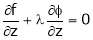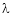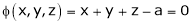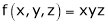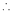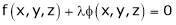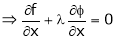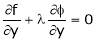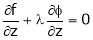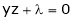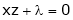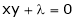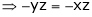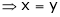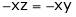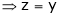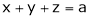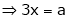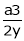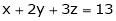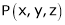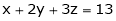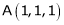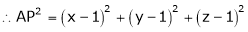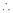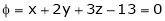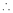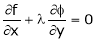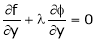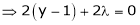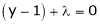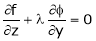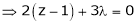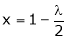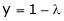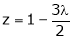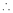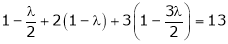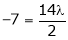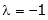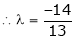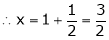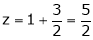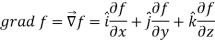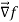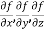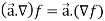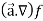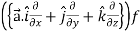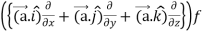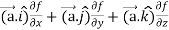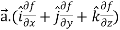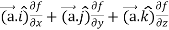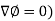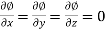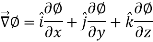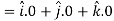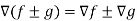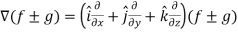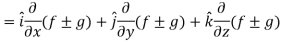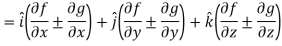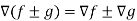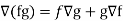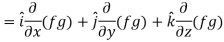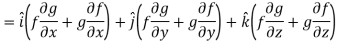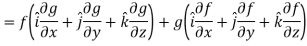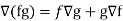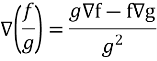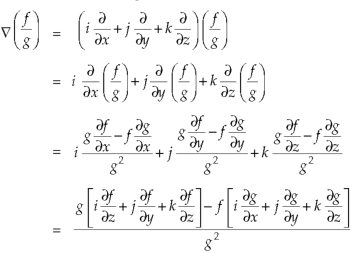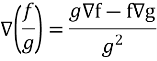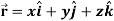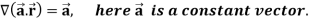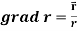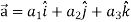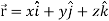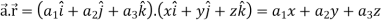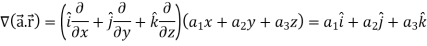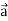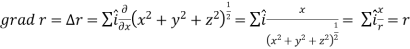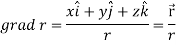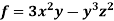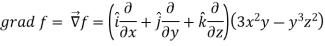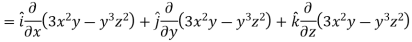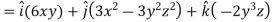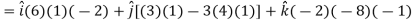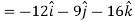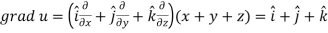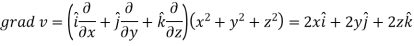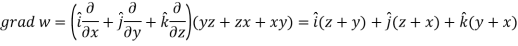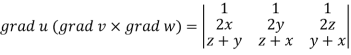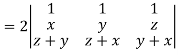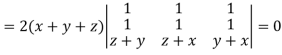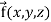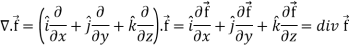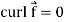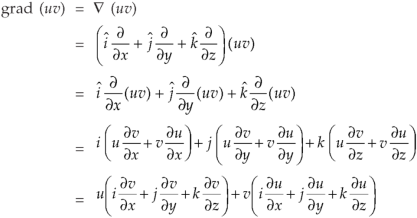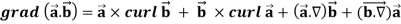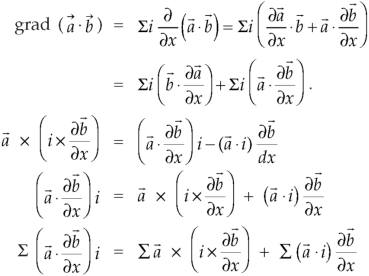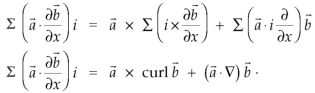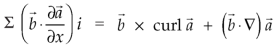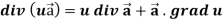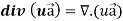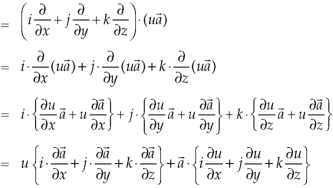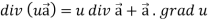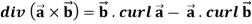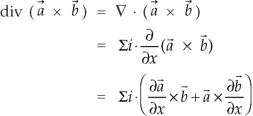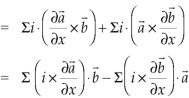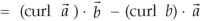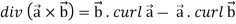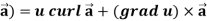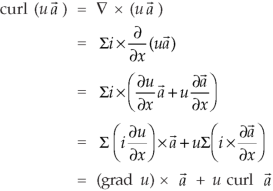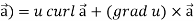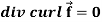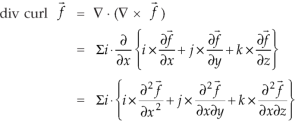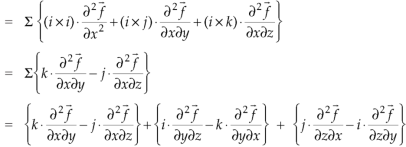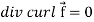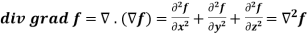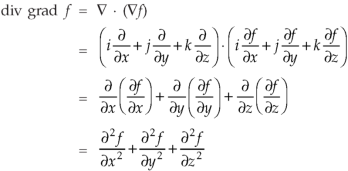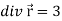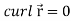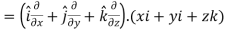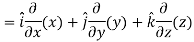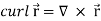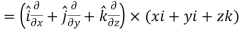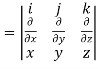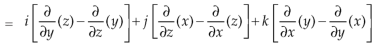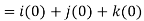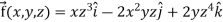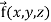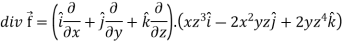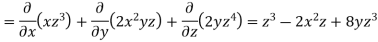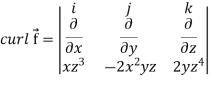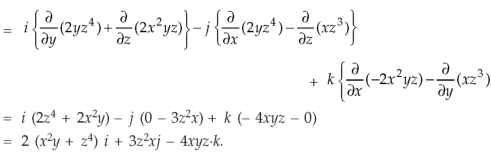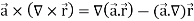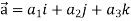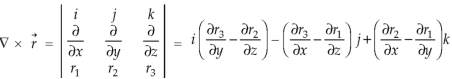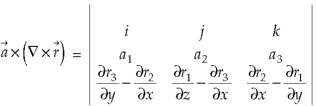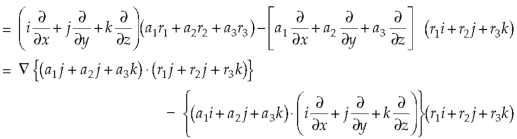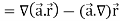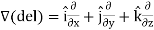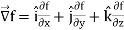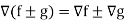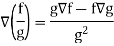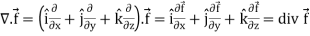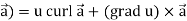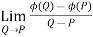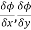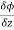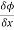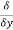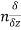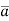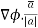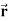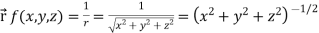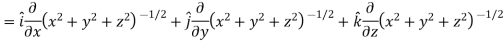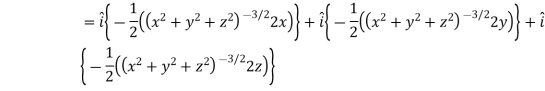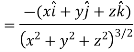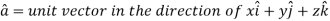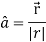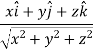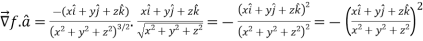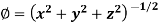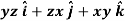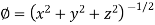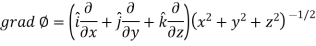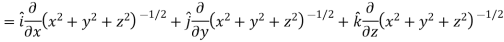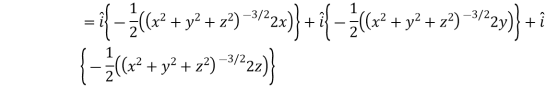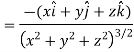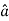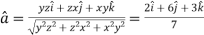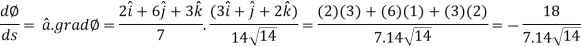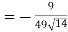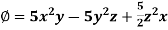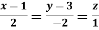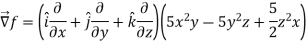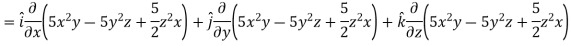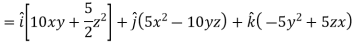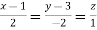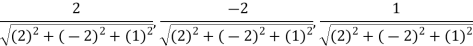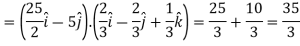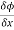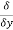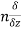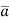UNIT-3
Multivariable calculus
Limits- The function f(x,y) is said to tend to limit ‘l’ , as x →a and y→bIff the limit is dependent on point (x,y) as x →a and y→b We can write this as,
Example-1: evaluate the Sol. We can simply find the solution as follows,
Example-2: evaluate Sol.
Example-3: evaluate Sol.
Conitinuity – At point (a,b) , a function f(x,y) is said to be continuous if,
Working rule for continuity- Step-1: f(a,b) should be well defined. Step-2: Step-3:
Example-1: Test the continuity of the following function-
Sol. (1) the function is well defined at (0,0) (2) check for the second step,
That means the limit exists at (0,0) Now check step-3:
So that the function is continuous at origin.
Example-2: check for the continuity of the following function at origin,
Sol. (1) Here the function is well defined at (0,0) (2) check for second step-
Limit f is not unique for different values of m So that the limit does not exists. Therefore the function is not continuous at origin. Steps to check for existence of limit- Step-1: find the value of f(x,y) along x →a and y→b Step-2: find the value of f(x,y) along x →b and y→a Note- if the values in step -1 and step-2 are same then we can say that the limits exist otherwise not. Step-3: if a →0 and b→0 then find the limit along y =mx , if the value does not contain m then limit exist, If it contains m then the limit does not exist. Note-1- put x = 0 and y = 0 in f , then find f1 2 - Put y = 0 and x = 0 In f then find x2 If f1 and f2 are equal then limit exist otherwise not. 3- put y = mx then find f3 If f1 = f2 ≠f3, limit does not exist. 4- put y = mx² and find f4, If f1 = f2 = f3 ≠f4 , limit does not exist If f1 = f2 = f3 = f4 , limit exist.
Example-1: Evaluate
Sol . 1.
2. Here f1 = f2 3. now put y = mx, we get
Here f1 = f2 = f3 Now put y = mx² 4. Therefore , F1 = f2 = f3 =f4 We can say that the limit exists with 0.
Example-2: evaluate the following-
Sol. First we will calculate f1 –
Here we see that f1 = 0 Now find f2,
Here , f1 = f2 Therefore the limit exists with value 0. Partial derivatives- First order partial differentiation- Let f(x , y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as
Now the partial derivative of f with respect to f can be written as
Note: a. while calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating , as constant. b. we apply all differentiation rules. Higher order partial differentiation- Let f(x , y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives. These are second order four partial derivatives: (a) (b) (c) (d) b and c are known as mixed partial derivatives. Similarly we can find the other higher order derivatives. Example-1: -Calculate f(x , y) = 3x³-5y²+2xy-8x+4y-20 sol. To calculate
= = 9x² - 0 + 2y – 8 + 0 – 0 = 9x² + 2y – 8 Similarly partial derivative of f(x,y) with respect to y is:
= = 0 – 10y + 2x – 0 + 4 – 0 = 2x – 10y +4. Example-2: Calculate f( x, y) = sin(y²x + 5x – 8) sol. To calculate
= cos(y²x + 5x – 8) = (y² + 50)cos(y²x + 5x – 8) Similarly partial derivative of f(x,y) with respect to y is,
= cos(y²x + 5x – 8) = 2xycos(y²x + 5x – 8)
Example-3: Obtain all the second order partial derivative of the function: f( x, y) = ( x³y² - xy⁵) sol.
Example-4: Find
Sol. First we will differentiate partially with repsect to r,
Now differentiate partially with respect to θ, we get
Example-5: if,
then find.
Sol-
Example-6: if Sol. Here we have, u = now partially differentiate eq.(1) w.r to x and y , we get
= Or
And now,
=
Adding eq. (1) and (3) , we get
Hence proved.
Total derivative- When we measure the rate of change of the dependent variable owing to any change in a variable on which it depends, when none of the variable is assumed to be constant. Let the function, u = f( x, y), such that x = g(t) , y = h(t) ᵡ Then we can write,
This is the total derivative of u with respect to t. Change of variable- If w = f (x, y) has continuous partial variables fx and fyand if x = x (t), y = y (t) are Differentiable functions of t, then the composite function w = f (x (t), y (t)) is a Differentiable function of t. In this case, we get,
Example-:1 let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t Then find Sol:
Where, f1 =
In this example f1 = 4 , f2 = 3 Also,
= 21t² + 2t – 3
Example-2: Find
Sol. as we know that by definition,
Example-3: if w = x² + y – z + sintand x + y = t, find
(a)
(b)
Sol. With x, y, z independent, we have t = x + y, w = x²+ y - z + sin (x + y). Therefore,
= 2x + cos (x + y) With x, t, z independent, we have Y = t-x, w= x² + (t-x) + sin t Thus
Example-4: If u = u( y – z , z - x , x – y) then prove that
Sol. Let,
Then,
By adding all these equations we get,
hence proved.
Example-5: if φ( cx – az , cy – bz) = 0 then show that ap + bq = c Where p =
Sol. We have, φ( cx – az , cy – bz) = 0 φ( r , s) = 0 where,
We know that,
Again we do,
By adding the two results, we get
Example-6: If z is the function of x and y , and x =
Sol. Here , it is given that, z is the function of x and y & x , y are the functions of u and v. So that,
And,
Also there is,
x = now,
From equation(1) , we get
And from eq. (2) , we get
Subtracting eq. (4) from (3), we get
= x Hence proved. |
Key takeaways
The function f(x,y) is said to tend to limit ‘l’ , as x →a and y→bIff the limit is dependent on point (x,y) as x →a and y→b We can write this as,
2. Conitinuity – At point (a,b) , a function f(x,y) is said to be continuous if,
(a) (b) (c) (d) |
Equation of a tangent plane-
And Equation of the normal to the plane-
Example: Find the equation of the tangent plane and normal line to the surface Sol. Here,
At point (1, 2, -1)-
Therefore the equation of the tangent plane at (1, 2, -1) is-
Equation of normal line is-
|
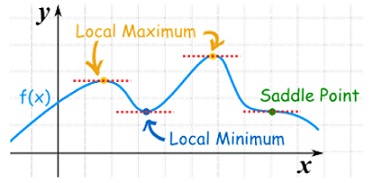
As we know that the value of a function at maximum point is called maximum value of a function. Similarly the value of a function at minimum point is called minimum value of a function. The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complement of each other. Maxima and Minima of a function of one variables If f(x) is a single valued function defined in a region R then Maxima is a maximum point Minima is a minimum point
Maxima and Minima of a function of two independent variables Let Then the point
Or For all positive and negative values of h and k. Similarly the point
Or For all positive and negative values of h and k. Saddle point: Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point. A point is a saddle point of a function of two variables if
at the point.
Stationary Value The value
i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of
4. (a) If (b) If (c) If (d) If
Example1 Find out the maxima and minima of the function
Given Partially differentiating (i) with respect to x we get
Partially differentiating (i) with respect to y we get
Now, form the equations Using (ii) and (iii) we get
Squaring both side we get
Or This show that Also we get Thus we get the pair of value as Now, we calculate
Putting above values in
At point (0,0) we get
So, the point (0,0) is a saddle point. At point
So the point In case
So the point Example2 Find the maximum and minimum point of the function
Partially differentiating given equation with respect to and x and y then equate them to zero
On solving above we get Also Thus we get the pair of values (0,0), ( Now, we calculate
At the point (0,0)
So function has saddle point at (0,0). At the point (
So the function has maxima at this point ( At the point (0,
So the function has minima at this point (0, At the point (
So the function has an saddle point at (
Example3 Find the maximum and minimum value of Let Partially differentiating given function with respect to x and y and equate it to zero
On solving (i) and (ii) we get
Thus pair of values are Now, we calculate
At the point (0,0)
So further investigation is required On the x axis y = 0 , f(x,0)=0 On the line y=x, At the point
So that the given function has maximum value at Therefore maximum value of given function
At the point
So that the given function has minimum value at Therefore minimum value of the given function
|
Key takeaways
Maxima is a maximum point Minima is a minimum point 3. A point is a saddle point of a function of two variables if
at the point.
|
Let Let
i.e. Also from
Let ‘
Solving equation (3), (4) (5) & we get values of x, y, z and
Solution: Let x, y, z be the three parts of ‘a’ then we get.
Here we have to maximize the product i.e.
i.e.
And
From (1)
Thus Hence their maximum product is 2. Find the point on plane Solution: Let
Under the condition
i.e.
From (2) we get From (3) we get From (4) we get
i.e.
y = 2
|
Suppose f(x, y, z) be the scalar function and it is continuously differentiable then the vector-
Is called gradient of f and we can write is as grad f. So that-
Here Properties of gradient- Property-1: Proof: First we will take left hand side L.H.S = = = = Now taking R.H.S, R.H.S. = = = Here- L.H.S. = R.H.S. Hence proved. Property-2: Gradient of a constant ( Proof: Suppose Then We know that the gradient-
= 0
Property-3: Gradient of the sum and difference of two functions- If f and g are two scalar point functions, then
Proof: L.H.S
Hence proved
Property-4: Gradient of the product of two functions If f and g are two scalar point functions, then
Proof:
So that-
Hence proved.
Property-5: Gradient of the quotient of two functions- If f and g are two scalar point functions, then-
Proof:
So that-
Example-1: If 1. 2. Sol. Suppose
Now taking L.H.S,
Which is Hence proved.
2. So that
Example: If Sol.
Now grad f at (1 , -2, -1) will be-
Example: If
Sol. Here-
Now-
Apply
Which becomes zero. So that we can say that grad u, grad v and grad w are coplanar vectors.
Divergence (Definition)- Suppose
Curl (Definition)- Curl of a vector function can be defined as-
Note- Irrotational vector- If
Vector identities: Identity-1: grad uv = u grad v + v grad u Proof:
So that graduv = u grad v + v grad u
Identity-2: Proof:
Interchanging
We get by using above equations-
Identity-3 Proof:
So that-
Identity-4 Proof:
So that,
Identity-5 curl (u Proof:
So that curl (u
Identity-6: Proof:
So that-
Identity-7: Proof:
So that-
Example-1: Show that- 1. 2. Sol. We know that-
2. We know that-
Example-2: If Sol. we know that-
Now-
Example-3: Prove that Note- here Sol. here So that
Now-
So that-
|
Key takeaways
If f and g are two scalar point functions, then
5. If f and g are two scalar point functions, then
6. If f and g are two scalar point functions, then-
7. 8. 9. If 10. grad uv = u grad v + v grad u 11. 12. curl (u |
Directional derivative Let ϕ be a scalar point function and let ϕ(P) and ϕ(Q) be the values of ϕ at two neighbouring points P and Q in the field. Then,
The directional derivative of ϕ in the direction l, m, n=l The directional derivative of ϕ in the direction of
Example: Find the directional derivative of 1/r in the direction
Sol. Here Now,
And We know that-
So that-
Now, Directional derivative =
Example: Find the directional derivative of
At the points (3, 1, 2) in the direction of the vector
Sol. Here it is given that-
Now at the point (3, 1, 2)-
Let
Now,
Example: Find the directional derivatives of Sol. Here
Direction ratio of the line Now directions cosines of the line are-
Which are Directional derivative in the direction of the line-
|
Key takeaways
|
References
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
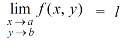
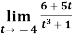
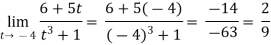
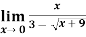
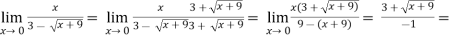
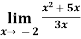
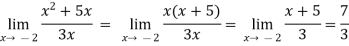
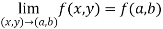
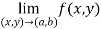
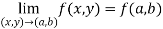
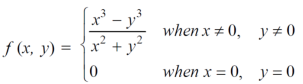
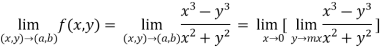
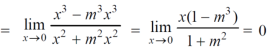
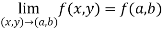
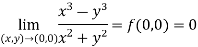
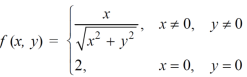
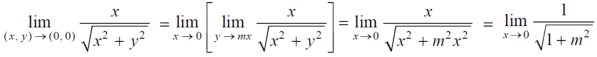
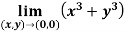
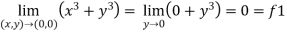
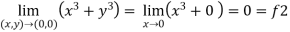
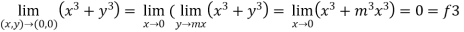
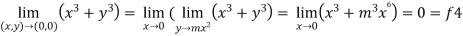
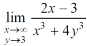
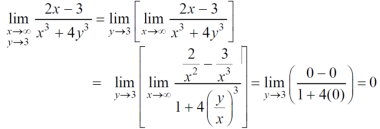
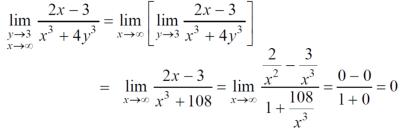

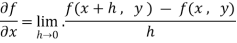
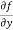
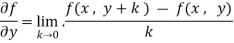
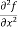
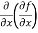
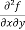
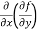
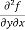
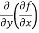
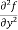
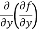
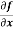
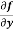
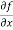


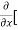
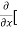
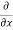
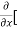
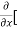
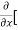
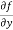

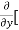
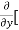
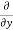
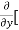
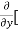
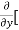
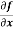
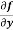
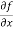
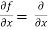
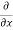
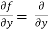
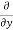
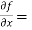
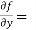
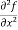
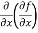
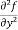
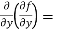
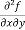
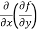
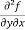

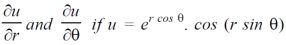
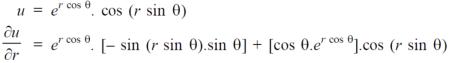
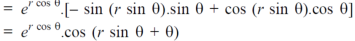
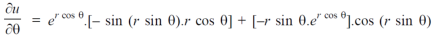
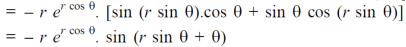
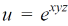
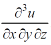
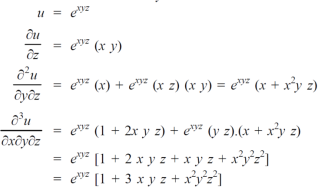
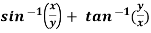

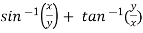
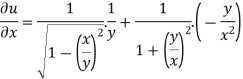
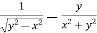
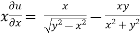
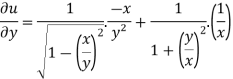
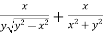
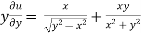
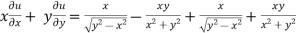
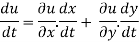
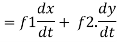

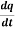
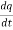
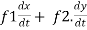
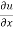
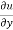
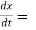
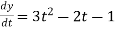

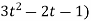
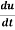
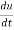
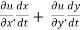
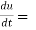
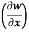
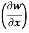

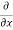
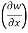
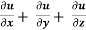
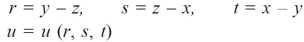

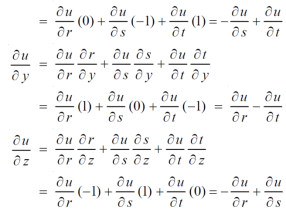
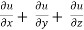

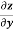
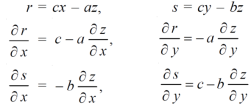
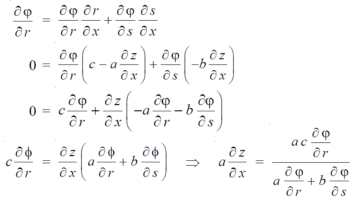
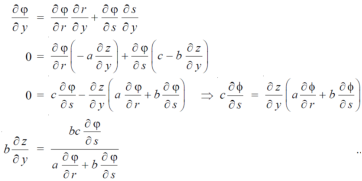
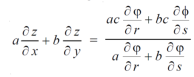

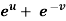
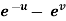


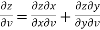
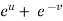
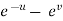
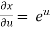
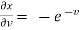
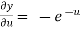

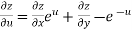
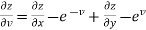
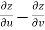
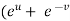
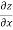
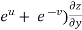

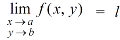
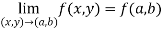
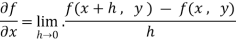

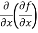
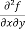
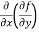
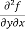
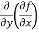
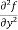
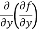
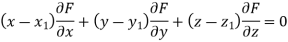

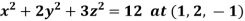
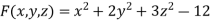
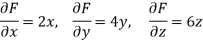
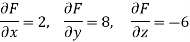

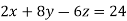
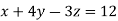
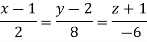
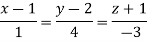

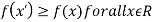

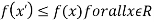


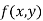
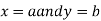
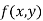
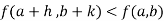
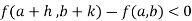
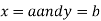

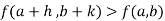

![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642930870_2262344.png)
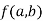

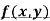
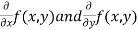
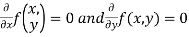
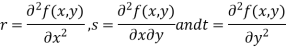
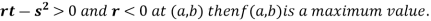
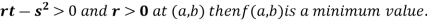
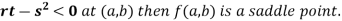

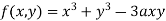
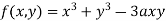
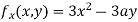
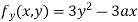



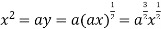
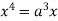
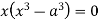
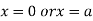
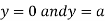
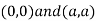

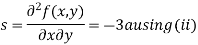
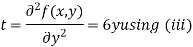
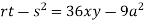
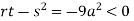

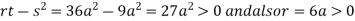
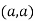
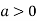

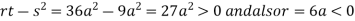
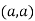
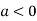
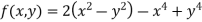
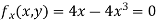
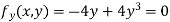
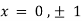
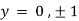



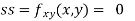
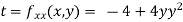
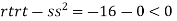
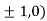
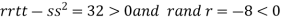

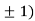
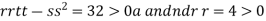
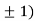
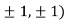

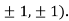
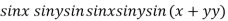
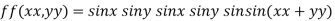

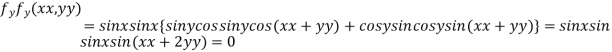
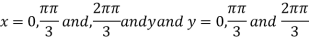
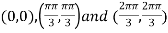
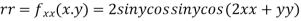
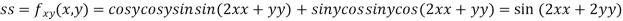
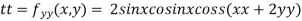
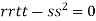
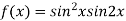
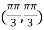
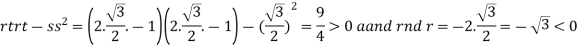
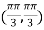
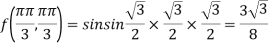
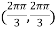
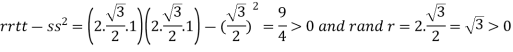
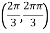


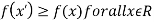
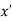
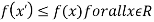
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642930875_4608498.png)