UNIT 5
Projection of Planes
- Plane is a two dimensional figure with limited/ unlimited two dimensions.
- Lamina is also a two dimensional figure with limited two dimensions. For example a sheet of paper is a lamina.
A plane is a two dimensional object having length and breadth only. Its thickness is always neglected. Various shapes of plane figures are considered such as square, rectangle, circle, pentagon, hexagon, etc.

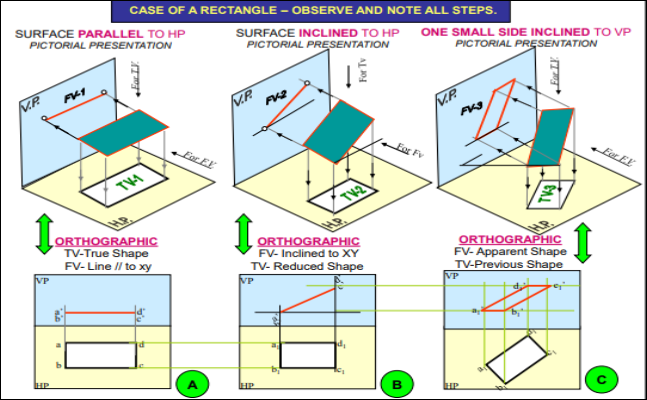
PROJECTIONS OF PLANES
- To draw their projections means F.V, T.V. & S.V.
What will be given in the problem?
- Description of the plane figure.
- It’s position with HP and VP.
In which manner it’s position with HP & VP will be described?
- Inclination of its SURFACE with one of the reference planes will be given
- Inclination of one of its EDGES with other reference plane will be given (Hence this will be a case of an object inclined to both reference Planes.)
Introduction
Plane figures or surfaces have only two dimensions, viz. Length and breadth. They do not have thickness. A plane figure may be assumed to be contained by a plane, and its projections can be drawn, if the position of that plane with respect to the principal planes of projection is known.
In this chapter, we shall discuss the following topics:
1. Types of planes and their projections.
2. Traces of planes.
Type of planes:
Planes may be divided into two main types:
(1) Perpendicular planes.
(2) Oblique planes.
Perpendicular planes:
These planes can be divided into the following sub-types:
(i) Perpendicular to both the reference planes.
(ii) Perpendicular to one plane and parallel to the other.
(iii) Perpendicular to one plane and inclined to the other.
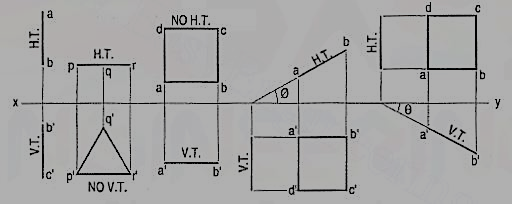
Perpendicular to both the reference planes (fig 1):
A square ABCD is perpendicular to both the planes. Its H.T. And V.T. Are in a straight-line perpendicular to xy.
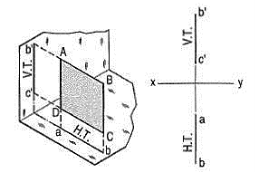
Figure 1
The front view b'c' and the top view ab of the square are both lines coinciding with the V.T. And the H.T. Respectively.
Perpendicular to one plane and parallel to the other plane:
a) Plane, perpendicular to the H.P. And parallel to the V.P. [fig. 12(i)]. A triangle PQR is perpendicular to the H.P. And is parallel to the V.P. Its H.T. Is parallel to xy. It has no V.T.
The front view p'q'r' shows the exact shape and size of the triangle. The top view pqr is a line parallel to xy. It coincides with the H.T.
(b) Plane, perpendicular to the V.P. And parallel to the H.P. [fig. 2(ii)]. A square ABCD is perpendicular to the V.P. And parallel to the H.P. Its V.T. Is parallel to xy. It has no H.T.
The top view abed shows the true shape and true size of the square. The front view a'b' is a line, parallel to xy. It coincides with the V.T.
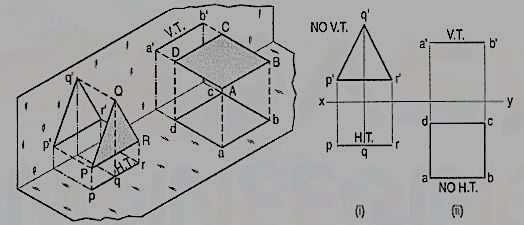
Figure 2
Perpendicular to one plane and inclined to the other plane:
A square ABCD is perpendicular to the H.P. And inclined at an angle φ to the V.P. Its V.T. Is perpendicular to xy. Its H.T. Is inclined at φ to xy.
Its top view ab is a line inclined at φ to xy. The front view a'b'c'd' is smaller than ABCD.
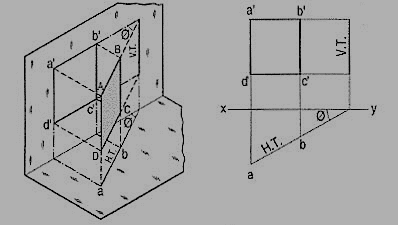
Figure 3
(b) Plane, perpendicular to the V.P. And inclined to the H.P. (fig. 3).
A square ABCD is perpendicular to the V.P. And inclined at an angle θ to the H.P. Its H.T. Is perpendicular to xy. Its V.T. Makes the angle e with xy. Its front view a'b' is a line inclined at θ to xy. The top view abed is a rectangle which is smaller than the square ABCD.

Figure 4
Fig. 4 shows the projections and the traces of all these perpendicular planes by third-angle projection method.
Use of Auxiliary Plane Method for solving the problems
A plane is a two dimensional object having length and breadth only. Its thickness is always neglected. Various shapes of plane figures are considered such as square, rectangle, circle, pentagon, hexagon, etc.

PROJECTIONS OF PLANES
- To draw their projections means F.V, T.V. & S.V.
What will be given in the problem?
- Description of the plane figure.
- It’s position with HP and VP.
In which manner it’s position with HP & VP will be described?
- Inclination of it’s SURFACE with one of the reference planes will be given
- Inclination of one of it’s EDGES with other reference plane will be given (Hence this will be a case of an object inclined to both reference Planes