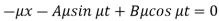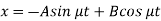Module 1
Ordinary Differential Equations-1
Ordinary differential equations
A differential equation is an equation with a function and one and more of its derivatives:
For example:
A differential equation with only single independent variable is known as ordinary differential equation.
Here we will learn about degree and order of an ordinary differential equation:
Order: the order is the highest derivative:
For example: (1)  + y³ = 8x, here it has only first derivative so it’s ‘first order’.
+ y³ = 8x, here it has only first derivative so it’s ‘first order’.
(2) 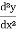 + y³ = 7x, here it has a second derivative so it’s ‘second order’ and so on.
+ y³ = 7x, here it has a second derivative so it’s ‘second order’ and so on.
Degree: Degree is known as the exponent of higher derivative.
For example:
(1)  + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
+ y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
(2)  +
+ 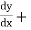 y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
Note- A solution to a differential equation which contains one or more arbitrary constants of integration is called general solution.
If additional information is given so that constant may be calculated the particular Solution. Additional information are boundary conditions.
Let’s understand how to solve differential equations:
(1) The solution of equations of the form 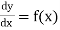
This type of equation can be solved by direction integration:
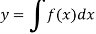
Example-1: Find the general solution of x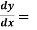 2 – 4x³
2 – 4x³
Solution: rearranging the given equation:
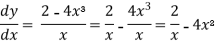
On integrating both sides,
y = 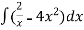 = 2 In x -
= 2 In x - 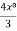 + c
+ c
This is the general solution.
Exampl-2: Find the particular solution of the differential equation 5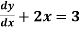 , given the boundary condition y = 1
, given the boundary condition y = 1 , when x = 2.
, when x = 2.
Solution: rearrange the diff. Equation,

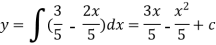
Which is the general solution.
Put the boundary conditions to find c,
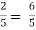 -
-  , which gives, c = 1
, which gives, c = 1
Hence the particular solution is,
y = 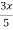 -
-  + 1.
+ 1.
(2) The solution of equation of the form 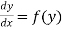 ,
,
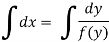
Example-1: Find the general solution of  = 3 + 2y
= 3 + 2y
Solution: here, 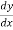 = 3 + 2y gives,
= 3 + 2y gives,
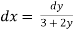 ,
,
Integrating both sides,
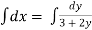 ,
,
By substitution, u = (3 +2y),
X =  In (3 + 2y) + c.
In (3 + 2y) + c.
Example-2: Determine the particular solution of (y² - 1)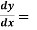 3y given that y =1 when x = 2
3y given that y =1 when x = 2 .
.
Solution: It gives,
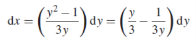
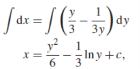
When putting the values, y =1, x = 2 ,
,
The particular solution will be,
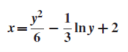
(3) The solution of equation of the form 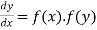
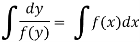
Example-1: Solve the equation 4xy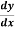 = y² - 1
= y² - 1
Solution: on separating variables, we get
( ) dy =
) dy = dx
dx
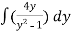 =
= 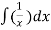
Using substitution, u = y² - 1
2In (y² - 1) = In x + c.
Example-2: Determine the particular solution of 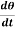 = 2
= 2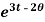 , given that t = 0, when θ = 0
, given that t = 0, when θ = 0
Solution:
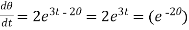 ,
,
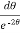 = 2
= 2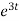 dt
dt
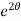 dθ =
dθ = 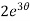 dt
dt
Now integrating both sides,
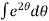 =
= 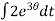
The general solution is,
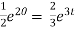 + c.
+ c.
When t = 0 and θ = 0, c = 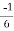
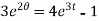
Linear and Bernoulli’s equation
A differential equation of the form
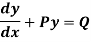
Is called linear differential equation.
It is also called Leibnitz’s linear equation.
Here P and Q are the function of x
Working rule
(1)Convert the equation to the standard form 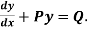
(2) Find the integrating factor.
(3) Then the solution will be y (I.F) = 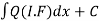
Example-1: Solve-
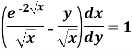
Sol. We can write the given equation as-
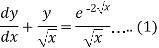
So that-
I.F. = 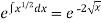
The solution of equation (1) will be-
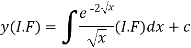
Or
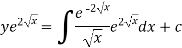
Or
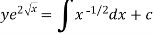
Or
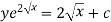
Example-2: Solve-
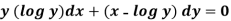
Sol.
We can write the equation as-

We see that it is a Leibnitz’s equation in x-
So that-
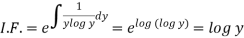
Therefore, the solution of equation (1) will be-
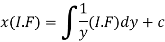
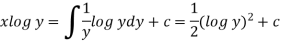
Or
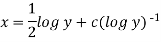
Example-3: Solve sin x 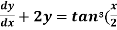 )
)
Solution: here we have,
Sin x 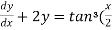 )
)
 which is the linear form,
which is the linear form,
Now,

Put tan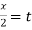 so that
so that  sec²
sec² dx = dt, we get
dx = dt, we get
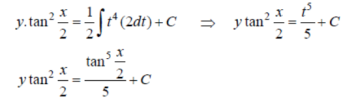
Which is the required solution.
Bernoulli’s equation-
The equation
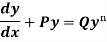
Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.
Working procedure to solve the Bernoulli’s linear equation-
Divide both sides of the equation -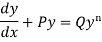
By  , so that
, so that
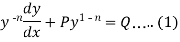
Put 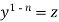 so that
so that 
Then equation (1) becomes-
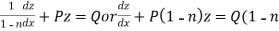 )
)
Here we see that it is a Leibnitz’s linear equations which can be solved easily.
Example: Solve 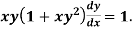
Sol.
We can write the equation as-
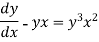
On dividing by 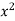 , we get-
, we get-
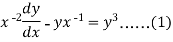
Put 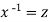 so that
so that 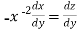
Equation (1) becomes,
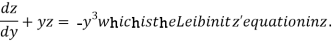
Here,
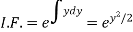
Therefore, the solution is-
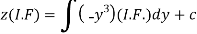
Or
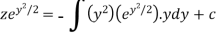
Now put 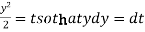

Integrate by parts-
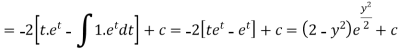
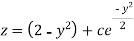
Or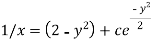
Example: Solve 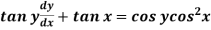
Sol. Here given,
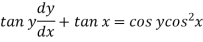
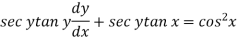
Now let z = sec y, so that dz/dx = sec y tan y dy/dx
Then the equation becomes-
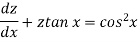
Here,
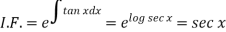
Then the solution will be-
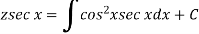
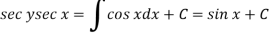
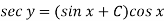
Example: Solve- 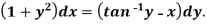
Sol. Here given-
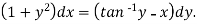
We can re-write this as-
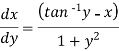

Which is a linear differential equation-
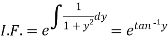
The solution will be-
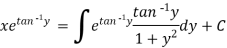
Put 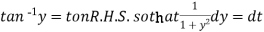
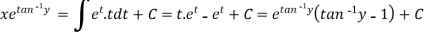
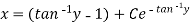
Exact Differential equations-
Definition-
An exact differential equation is formed by differentiating its solution directly without any other process,
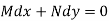
Is called an exact differential equation if it satisfies the following condition-
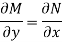
Here 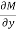 is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and 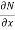 is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Step by step method to solve an exact differential equation-
1. Integrate M w.r.t. x keeping y constant.
2. Integrate with respect to y, those terms of N which do not contain x.
3. Add the above two results as below-
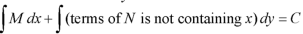
Example-1: Solve 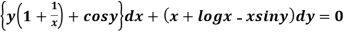
Sol.
Here M = 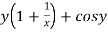 and N =
and N = 
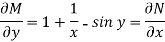
Then the equation is exact and its solution is-

Example-2: Solve-
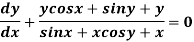
Sol. We can write the equation as below-

Here M = 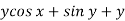 and N =
and N = 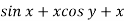
So that-
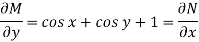
The equation is exact and its solution will be-
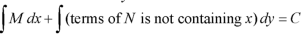
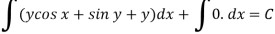
Or
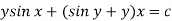
Example-3: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution. Here the equation is the form of M (x,y) dx + N (x,y) dy = 0
But we will check for exactness,
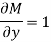
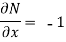
These are not equal results, so we can say that the given diff. Eq. Is not exact.
The differential equations of first order and higher degree are the form of f (x, y, p) = 0.
Dy/dx will occur in higher degrees, so that for convenience we denote dy/dx by ‘p’.
There are total three cases-
Case-1: Equation solvable for ‘p’-
A differential equation of the first order and n’th order is of the form-
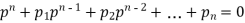
Where  are the functions of x and y.
are the functions of x and y.
The general solution of this equation can be written as-
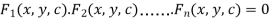
Case-2: Equation solvable for ‘y’-
1. Differentiate the given equation with respect to “x”
2. Eliminate ‘p’ from the given equation.
3. The eliminant is the required solution.
Case-3: Equation solvable for ‘x’-
1. Differentiate the given equation with respect to ‘y’..
2. Solve the equation for ‘p’.
3. Eliminate ‘p’, by putting the value of ‘p’ in the given equation.
4. The eliminant will be the required solution.
Example: Solve-
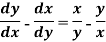
Sol.
The given equation can be written as-
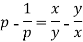
Where p = dy/dx
Or
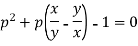
Now factorising-
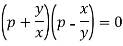
Thus, we have-
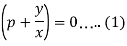
And

Now from equation (1)-
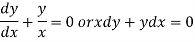
That means-
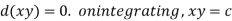
Now from equation (1)-
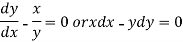
Integrating 
Thus
Xy = c or 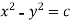 is the required solution.
is the required solution.
Example: Solve:
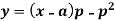
Sol.
We have-
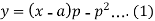
Now differentiate (1) with respect to ‘x’, we get-
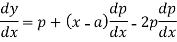
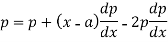
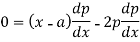
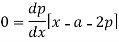
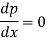
On integrating, we get p = c
Putting these values in equation (1)-
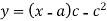
Example: Solve-

Sol.
On solving for x, we get-
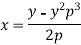
On differentiating with respect to y,
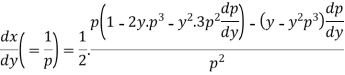
Or
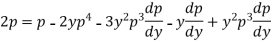
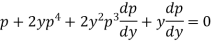
Or
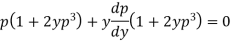
Or
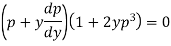
Which gives-
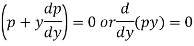
Integrating py = c
Thus, eliminate from the given equation and (1), we get-
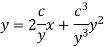
Which is the required solution.
Second order linear homogeneous equations with constant coefficients
A homogeneous linear ordinary differential equation with constant coefficients is an ordinary differential equation in which coefficients are constants, all terms are linear, and the entire differential equation is equal to zero,
The form of second order linear differential equation with constant coefficients is,
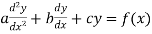 ,
,
Where a,b,c are the constants.
Let, aD²y+bDy+cy = f(x), where d² = 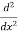 , D =
, D = 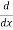
∅(D)y = f(x) , where ∅(D)y = aD²y+bDy+cy
Here first we solve, ∅(D)y = 0, which is called complementary function(C.F)
Then we find particular integral (P.I)
P.I. = 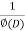 f(x)
f(x)
General solution = C.F. +P.I.
Let’s do an example to understand the concept,
Example1: Solve (4D² +4D -3)y = 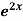
Solution: Auxiliary equation is 4m² +4m – 3 = 0
We get, (2m+3) (2m – 1) = 0
m = 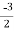 ,
, 
Complementary function: CF is A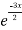 + B
+ B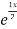
Now we will find particular integral,
P.I. =  f(x)
f(x)
= 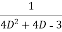 .
. 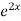
= 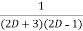 .
. 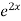
= 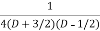 .
. 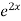
=  .
.  =
= 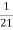 .
. 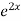
General solution is y = CF + PI
= A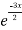 + B
+ B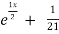 .
. 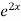
Non-Homogeneous equations of higher order with constant coefficient of R.H.S. Terms of the type 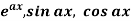
Linear differential equation is those in which the independent variable and its derivative occur only in the first degree and are not multiplied together.
Thus, the general linear differential equation of the n’th order is of the form
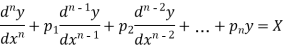
Where  and X are function of x.
and X are function of x.
Linear differential equation with constant co-efficient are of the form-
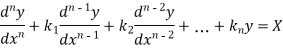
Where  are constants.
are constants.
Rules to find the complementary function-
To solve the equation-
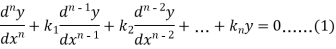
This can be written as in symbolic form-
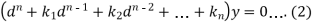
Or-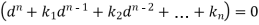
It is called the auxiliary equation.
Let 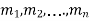 be the roots-
be the roots-
Case-1: If all the roots are real and distinct, then equation (2) becomes,
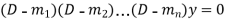
Now this equation will be satisfied by the solution of 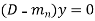
This is a Leibnitz’s linear and I.F. = 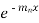
Its solution is-
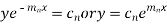
The complete solution will be-
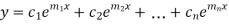
Case-2: If two roots are equal 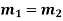
Then complete solution is given by-
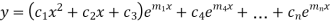
Case-3: If one pair of roots be imaginary, i.e. 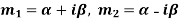 then the complete solution is-
then the complete solution is-
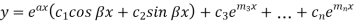
Where 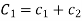 and
and 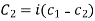
Case-4: If two points of imaginary roots be equal-
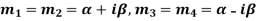
Then the complete solution is-

Example-Solve 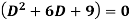
Sol.
Its auxiliary equation is-
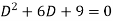
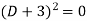
Where-
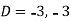
Therefore, the complete solution is-
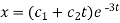
Inverse operator-
 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
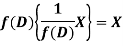
So that 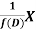 satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 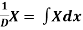
2. 
Rules for finding the particular integral-
Let us consider the equation-
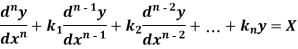
Or in symbolic form-

So that-
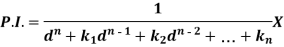
Now-
Case-1: When X = 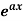
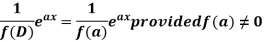
In case f(a) = 0, then we see that the above rule will not work,
So that-
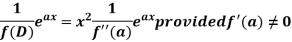
Example: Find the P.I. Of (D + 2)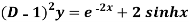
Sol.
P.I. = 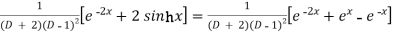
Now we will evaluate each term separately-
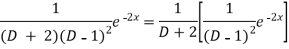
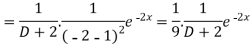
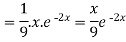
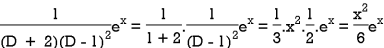
And
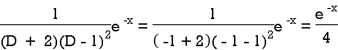
Therefore-
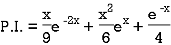
Example: Solve (D – D’ – 2) (D – D’ – 3) z = 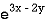
Sol.
The C.F. Will be given by-
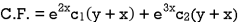
Particular integral-

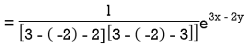
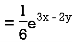
Therefore, the complete solution is-
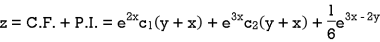
Case-2: when X = sin( ax + b) or cos (ax + b)
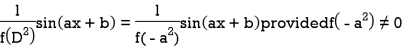
In case  then the above rule fails.
then the above rule fails.
Now-

And if 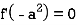
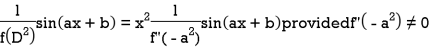
Similarly-
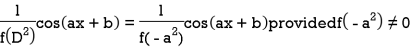
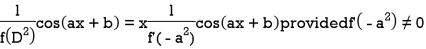
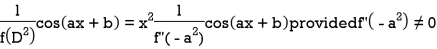
Example: Find the P.I. Of 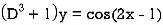
Sol.
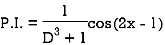
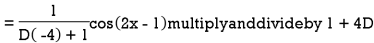
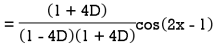
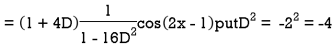
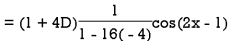
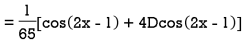
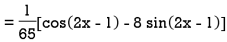
Example: Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)
Sol.
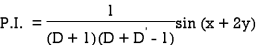
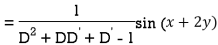
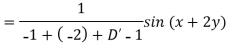
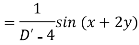
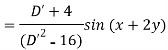
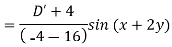

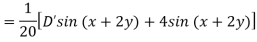
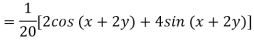
Example: Find P.I. Of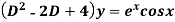
Sol. P.I = 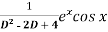
Replace D by D+1
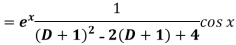
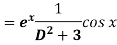
Put 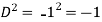
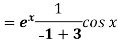
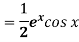
Polynomials in x, 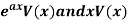 -
-
Let us consider the equation-
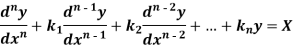
Or in symbolic form-

So that-
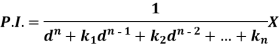
Now-
Case-1: When  , V is the function of x.
, V is the function of x.
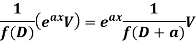
Case-2: When X is any other function of x.
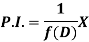
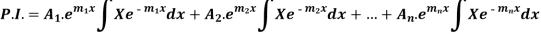
Example: Find P.I. Of 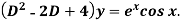
Sol.
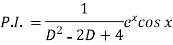
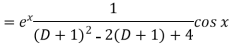

Put 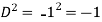
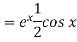
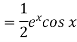
Working method to find the complete solution of an equation-
Example: Solve 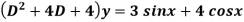
Sol.
Here first we will find the C.F.-
Its auxiliary equation will be-

Here we get-
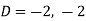
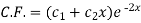
Now we will find P.I.-
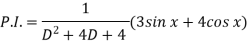
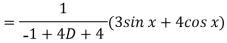
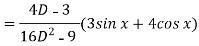
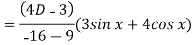
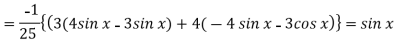
Now the complete solution is-

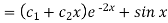
Example: Solve-
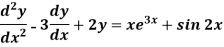
Sol.
The given equation can be written as-
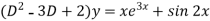
Its auxiliary equation is-

We get-

So that the C.F. Will be-
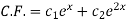
Now we will find P.I.-
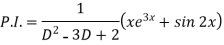
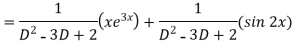
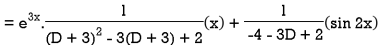
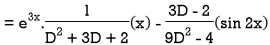
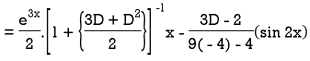
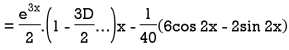
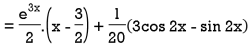
Therefore, the complete solution is-
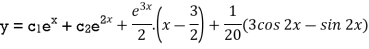
A homogeneous linear ordinary differential equation with constant coefficients is an ordinary differential equation in which coefficients are constants, all terms are linear, and the entire differential equation is equal to zero,
The form of second order linear differential equation with constant coefficients is,
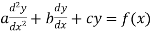 ,
,
Where a,b,c are the constants.
Let, aD²y+bDy+cy = f(x), where d² =  , D =
, D = 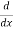
∅(D)y = f(x), where ∅(D)y = aD²y+bDy+cy
Here first we solve, ∅(D)y = 0, which is called complementaryfunction (C.F)
Then we find particular integral (P.I)
P.I. = 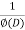 f(x)
f(x)
General solution = C.F. +P.I.
Example: Solve (4D² +4D -3) y = 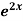
Sol. Auxiliary equation is 4m² +4m – 3 = 0
We get, (2m+3) (2m – 1) = 0
m = 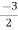 ,
, 
Complementary function: CF is A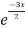 + B
+ B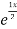
Now we will find particular integral,
P.I. = 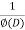 f(x)
f(x)
= 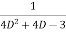 .
. 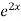
=  .
. 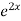
= 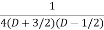 .
. 
= 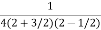 .
. 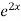 =
= 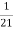 .
. 
General solution is y = CF + PI
= A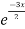 + B
+ B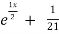 .
. 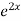
Euler-Cauchy equation-
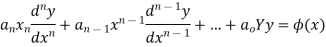
Where, 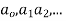 are constant is called homogenous equation.
are constant is called homogenous equation.
Put, 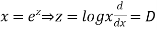
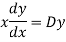
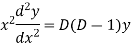

Example. Solve 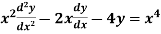
Ans. Put, 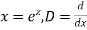
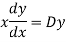
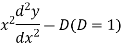
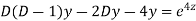
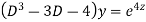
AE is 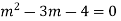
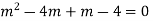
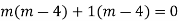
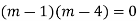
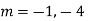
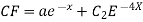
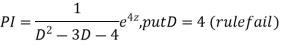
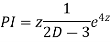
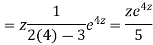

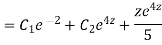
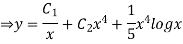
Example. 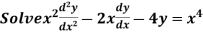
Ans. Putting, 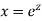
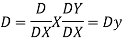
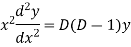
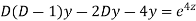
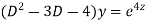
AE is 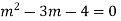
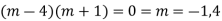
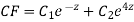
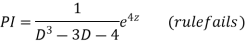
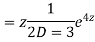
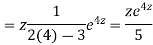
CS = CF + PI
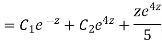
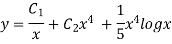
Example: Solve 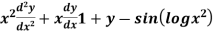
Ans. Let, 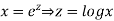
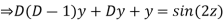

AE is 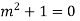
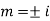
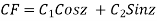
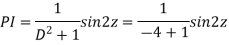
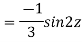
y= CF + PI
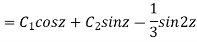
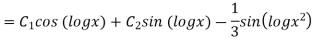
Example: Solve 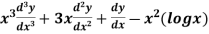
Ans. Let, 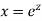 so that z = log x
so that z = log x
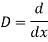
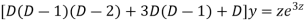
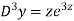
AE is 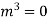
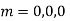
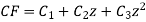
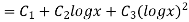
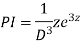
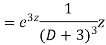
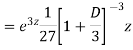
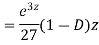
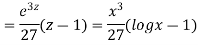

If two or more dependent variables are functions of a single independent variable, then the equations involving their derivatives are called simultaneous equations.
These equations are being solved by the process of elimination
Example: Solve the following differential equations-

Sol.
We have-

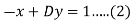
Multiply (1) by D, we get-
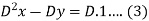
Now add (2) and (3), we get


Auxiliary equation is-
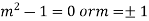
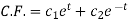
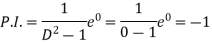
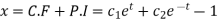
From (1),
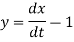
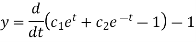
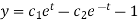
And
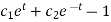
Example: Solve-
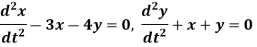
Sol.
Here we


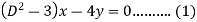
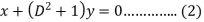
Operate equation (2) by 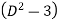 , we get-
, we get-
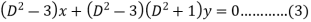
Subtract (3) from (1)-

A.E-
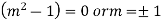

From equation (2), we get-
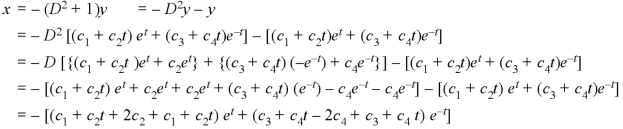
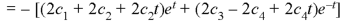
These are the required solutions.
Example: The equations of motions of an object are given by-
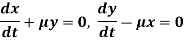
Find the path of the object.
Sol.
Put d/dt = D, then the equations become-
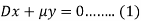

On multiplying (1) by 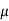 and (2) by D, we get-
and (2) by D, we get-

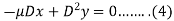
Add (3) and (4), we get-
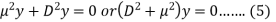
Now we need to solve (5) to get the value of y-
A.E.-
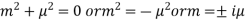
So that-
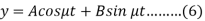
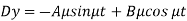
Now, on putting the value of Dy in (2), we get-