Unit 3
Magnetic field
It involves the interaction of magnetic field and current carrying conductor placed in it. The operation sequence is as follow
- Development of individual field
- Interaction of two magnetic fields
- Force exerted on the conduction
- Development of individual field
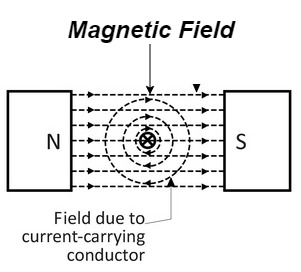
- Let a straight conductor is placed in the magnetic field produced by permanent magnet.
- Let current flowing through the conductor is out of the plane of the paper.
- The magnetic field produced by conductor is shown above
2. Interaction of two magnetic field
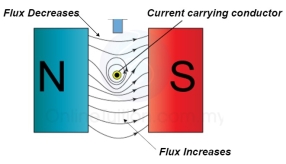
At the top flux lines produced by the magnet and conductor are in opposite direction to each other and hence cancel each other.
At the bottom individual fields are in same direction they will add each other.
3. Force excreted on the conductor
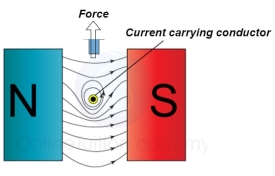
The lines of force on the bottom exert a force on the conductor in the upward direction as shown above.
Hence mechanical force is exerted on the conductor from high flux line area towards the low flux line area (top).
The magnetically of force experienced by the current carrying conductor placed in a magnetic field is given by
F = B I ɺ sin Ɵ newton
Where F = Force exerted
B = Flux density
ɺ = length of conductor
I = current
Ɵ = angle between conductor and magnetic field.

The magnetic circuit can be defined as the closed path traced by magnetic line of force such magnetic circuit is associated with different magnetic quantities such as MMF, flux, flux density, magnetic field strength
We know that H = 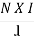
And B = μ H
Put value of H
 B = μ x
B = μ x 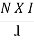
But μ = μₒμ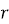
 B = μ₀μ
B = μ₀μ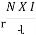
But B = 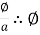 = B x a
= B x a
Ø =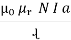
- Numerical on F = B I ɻ sin
- The atoms of ferromagnetic substances have permanent dipole moment present in domains.
- Atomic dipoles in ferromagnetic substances are oriented in the same direction as the external magnetic field.
- The magnetic dipole moment is large and is in the direction of the magnetizing field.
- The intensity of magnetization (M) is very large and positive and varies linearly with the magnetizing field (H). Hence saturation depends on the nature of the material.
- The magnetic susceptibility is very large and positive. Magnetic susceptibility Xm = M / H, where M is the intensity of magnetization and H is the strength of the applied magnetic field.
- The magnetic flux density of the material will be very large and positive. Magnetic field lines become very dense inside ferromagnetic materials. Magnetic flux density B = 0 (H + M), where 0 is the magnetic permittivity of free space, H is the strength of the applied magnetic field and M is the intensity of magnetization.
- The relative permeability is also very large and varies linearly with the magnetizing field the field inside the material is much stronger than the magnetizing field. They have a tendency of pulling in a large number of lines of force by the material. Relative permeability of material r = 1 + m
- Ferromagnetic substances are strongly attracted by the field. So in a nonuniform field, they have a tendency to stick at the poles where the field is strongest.
- If a ferromagnetic powder is placed in a watch glass placed on two poles pieces which are sufficient apart then powder accumulates at sides and shows depression in the middle because the field is strongest at poles.
- When a ferromagnetic substance is liquefied, it loses ferromagnetic properties due to higher temperature.
What is Self Induction?
When there is a change in the current or magnetic flux of the coil, an opposed induced electromotive force is produced. This phenomenon is termed as Self Induction. When the current starts flowing through the coil at any instant, it is found that that the magnetic flux becomes directly proportional to the current passing through the circuit. The relation is given as:
ϕ= I
ϕ = L I
Where L is termed as self-inductance of the coil or the coefficient of self-inductance. The self-inductance depends on the cross-sectional area, the permeability of the material or the number of turns in the coil.
The rate of change of magnetic flux in the coil is given as,
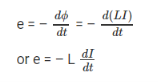
What is Mutual Induction?
We take two coils, and they are placed close to each other. The two coils are P- coil (Primary coil) and S- coil (Secondary coil). To the P-coil, a battery, and a key is connected wherein the S-coil a galvanometer is connected across it. When there is a change in the current or magnetic flux linked with two coils an opposing electromotive force is produced across each coil, and this phenomenon is termed as Mutual Induction. The relation is given as:
ϕ = I
ϕ = M I
Where M is termed as the mutual inductance of the two coils or the coefficient of the mutual inductance of the two coils.
The rate of change of magnetic flux in the coil is given as,
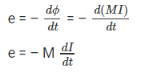
Magnetic field can be of permanent magnet or electro-magnet. Both magnetic fields store some energy. Permanent magnet always creates the magnetic flux and it does not vary upon the other external factors. But electromagnet creates its variable magnetic fields based on how much current it carries. The dimension of this electro-magnet is responsible to create the strength the magnetic field and hence the energy stored in this electromagnet.
First we consider the magnetic field is due to electromagnet i.e. a coil of several no. Turns. This coil or inductor is carrying current I when it is connected across a battery or voltage source through a switch.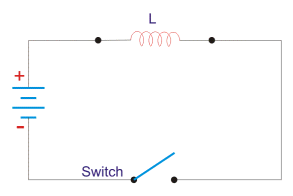
Suppose battery voltage is V volts, value of inductor is L Henry, and current I will flow at steady state.
When the switch is ON, a current will flow from zero to its steady value. But due to self induction a induced voltage appears which is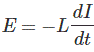
this E always in the opposite direction of the rate of change of current.
Now here the energy or work done due to this current passing through this inductor is U.
As the current starts from its zero value and flowing against the induced emf E, the energy will grow up gradually from zero value to U.
dU = W.dt, where W is the small power and W = – E.I
So, the energy stored in the inductor is given by
Now integrate the energy from 0 to its final value.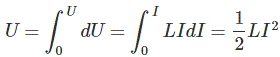
Again,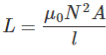
as per dimension of the coil, where N is the number of turns of the coil, A is the effective cross-sectional area of the coil and l is the effective length of the coil.
Again,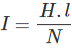
Where, H is the magnetizing force, N is the number of turns of the coil and l is the effective length of the coil.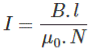
Now putting expression of L and I in equation of U, we get new expression i.e.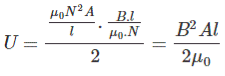
So, the stored energy in a electromagnetic field i.e. a conductor can be calculated from its dimension and flux density.
The end to end connection of two or more inductors is called “series connection of inductors”. In this connection the inductors are connected in series so the effective turns of the inductor increase. The series connection of the inductors is shown in below diagram
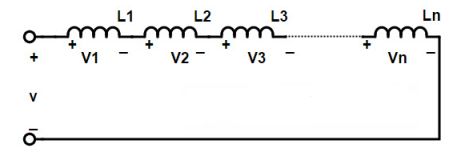
The inductance of series connected inductors is calculated as the sum of the individual inductances of each coil since the current change through each coil is same.
This series connection is similar to that of the resistors connected in series, except the resistors are replaced by inductors. If the current I is flowing in the series connection and the coils are L1, L2, and so on, the common current in the series inductors is given by
ITotal = IL1 = IL2 = IL3. . . = In
If the individual voltage drops across each coil in this series connection are VL1, VL2, V¬L3, and so on, the total voltage drop between the two terminals VT is given by
VTotal = VL1 + VL2 + VL3…. + Vn
As we know that the voltage drop can be represented in terms of self inductance L, this implies
V = L di/ dt.
This can also be written as
LT di/dt = L1 di/dt + L2 di/dt + L3 di/dt + . . . + Ln di/dt
Therefore, the total inductance is
LTotal = L1 + L2 + L3 + ….. + Ln
When ac supply is given the inductor present in the circuit stores the energy and flux is generated. Let I be the ac current passing through coil of N turns.
φm = maximum flux in core
ω = 2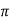 f
f
f is frequency in Hz
According to faradays law flux changes with respect to coil emf induced will be
e= N φm ω cos ωt V
E = rms value = 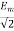 = N φm ω/
= N φm ω/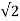
E= 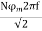 = 4.44 fN φm
= 4.44 fN φm
The sign of e.m.f induced must be determined according to len’s law, opposing the changes in the flux. The current and flux are in phase as current produces flux instantaneously.
Current carrying coil:

The magnetic field lines are concentric circles at every point of a current carrying circular loop. The direction of magnetic field of every section of the circular loop can be found by using the right-hand thumb rule.
- At the centre of the circular loop, magnetic field lines are straight.
- Each segment of circular loop carrying current produces magnetic field lines in the same direction with in the loop.
- The direction of magnetic field at the centre of circular coil is perpendicular to the place of the coil. i.e. along the axis of the coil.
Factors affecting the strength of magnetic field
- The magnitude of magnetic field is directly proportional to the magnitude of current through the loop. i.e. B∝I.
- The magnitude of magnetic field is inversely proportional to the radius of the circular loop. i.e. B∝1/r.
Que) The amount of flux present in around magnetic bar was measured at 0.013 weber. If the material has a diameter of 14cm, calculate the flux density.
Sol: Area=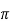 r2
r2
Diameter=2r
r=14/2=7cm=0.07m
Area=3.14 x 0.072=0.0154m2
Flux Density B== A=0.013/0.0154=0.843 Tesla
A=0.013/0.0154=0.843 Tesla
Que) Calculate the radius of the material having flux density of 0.5 T and flux present around the magnetic bar is 0.02T.
Sol: Flux Density B=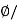 A
A
A= 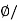 B=0.02/0.5=0.04 m2
B=0.02/0.5=0.04 m2
Area=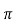 r2
r2
r=0.113m
The magnetic field exerts a force on a current carrying wire in the direction given by right hand rule. The force on a charge moving with vd velocity is
F=q vdBsin 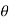
B is uniform over the length of the wire and zero otherwise.
F= (q vdBsin 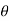 )N
)N
N: number of charge carriers in the wire
N=nV
n=number of charge carrier /unit volume
V= volume of wire in the field
V=AI
A=cross-sectional area
F= (q vdBsin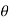 )nAl
)nAl
F= nqAvd)lBsin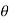
F= I l Bsin 
Faraday’s Laws of Electromagnetic Induction consists of two laws. The first law describes the induction of emf in a conductor and the second law quantifies the emf produced in the conductor
i) Faradays First law of EMI: Whenever a conductor is placed in a varying magnetic field, an electromotive force is induced. If the conductor circuit is closed, a current is induced which is called induced current.
Ii) Faradays Second law of EMI: The induced emf in a coil is equal to the rate of change of flux linkage.
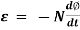
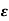 = electromotive force
= electromotive force
N = Number of turns
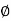 = magnetic flux
= magnetic flux
- Increase in the number of turns in the coil increases the induced emf
- Increasing the magnetic field strength increases the induced emf
- Increasing the speed of the relative motion between the coil and the magnet, results in the increased emf
The sign of e.m.f induced must be determined according to len’s law, opposing the changes in the flux. The current and flux are in phase as current produces flux instantaneously. Now induced e.m.f is cosine term and thus leads the flux and current by .this is called back e.m.f as it opposes the applied voltage. The resistance drop is very small and is neglecte3d in most of the electromagnetic devices.
I Ø transformers and electrostatics
- Types of transformers
Acc to input supply : I phase and 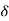 phase
phase
Acc to construction : core and shell type
Acc to 0/P : step up and step down
Construction of transformers (study only for MCQs)
- Laminated steel core
Material used for core is (silicon steel) it is used for its (high permeability) and (low magnetic reluctance)  magnetic field produced is very strong
magnetic field produced is very strong
The core is formed of (stacks of laminated thin steel sheets) which are electrically isolated from each other. They are typically (0.35 to 0.5 mm thick)
We can used 2 ‘L’ shaped sheets or 2  shaped sheets for laminations
shaped sheets for laminations
Construction and types
- There 2 types of winding
- Concentric or cylindrical
- Sandwiched type
- Cylindrical
L.V. = low voltage H.V. = high voltage are mounted on same limb to minimum leakage.
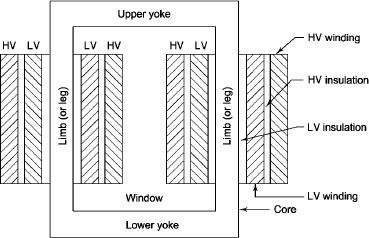
L.V. Winding placed inside and H.V. Winding placed outside with (proper insulation between the winding as it is easy to insulated L.V. Winding) than H.V. Winding.
2. Sandwiched
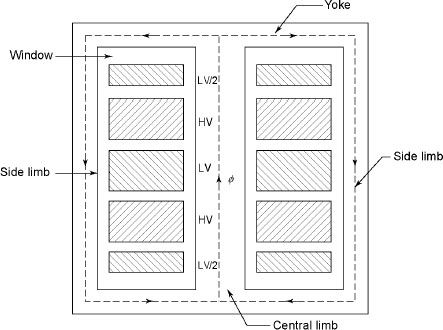
The H.V. And L.V. Winding are divided into no. Of small coils and there small windings are interleaved.
(the top and bottom winding are L.V. Coils because they are close to core)
- Transformer tank : wholes assembly of winding and core placed inside the Transformer tank (sheet metal tank) which is filled with Transformer oil or insulating oil which acts as an (insulator or coolant ) MCQ
- Transformer oil : (The function of oil is to remove efficiently the heat generated in core and in winding)
- Moisture should not be allowed which creeps the insulation which achieved by closed Transformer tank.
(To increase cooling surface are tubes or fins are provided)
- Conservator tank : above tank T/F tank there is one small tank in which same empty space is always provided above the oil level. (this space is required for oil to expand or contract due to temperature change) MCQ
However during contraction outside air can have moisture which will deteriorate the insulating properly of oil.
- Breather : the air goes in or out through the breather (To reduce the moisture content of their air . Same drying agents such as (silica gel or) calcium chloride) is used in the breather (The dust particles present in air are also removed by breather)
- Buccholz Relay : (for incipient (slowly increasing) faults
There is pipe connecting rain tank and conservator. On the pipe a protective device called Buccholz Relay is mounted.
When the Transformer is about to be faulty and draw range current the oil becomes very hot and decompose.
During this process different types of gases are liberated.(The Bucchoz Relay get operated by these gases) and gives an alarm to the operator. ɡȴ the fault continues to persist then there lay will trip off main circuit breaker to protect the Transformer.
- Explosion Vent :
An explosion Vent or relief value is the bent up pipe filled on the main tank.
(The explosion vent consist of aluminium of oil ) when the T/F becomes faulty the cooling oil get decomposed and various types of gases are liberated
(ɡȴ the gas pressure exodus certain level then the aluminium of oil (diagram) in explosion vent will burst) to release pressure. The will save main tank from getting damaged.
It is a static device which can transfer electrical energy from one ac circuit to another ac circuit without change in frequency
It can increase or decrease the voltage but with corresponding decrease or increase in current
It works on Principle 
“Mutual Induction”
A major application of transformer is to increase voltage before transmitting electrical energy over a long distance through conductors and to again reduce voltage at place where it is to be used.
Symbol
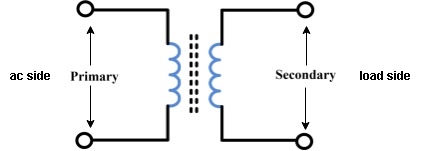
- Primary winding : (ac supply side) For MCQs
The winding which is connected to supply is called primary side
2. Secondary winding : (load side) for MCQs
The winding which is connected to load is called as secondary winding
4.1 Principle of operation,
- Working :
It works on principle of mutual Induction ie “when 2 coil are inductively coupled and if current in one coil is changed uniformly then an emf get induced in another coil”
- When alternating voltage V1 is applied to primary winding am alternating current I1 flows in it producing alternating flux in the core.
- As per Faradays Law of Electromagnetic Induction 1 an emf E1 is induced in the primary winding E = N1
- The emf induced in the primary winding is nearly equal and opporite to applied voltage V1
- Assuming leakage flux to be negligible almost whole flux produced in primary winding links with secondary winding thence emf induced in the secondary winding E2 = N2
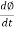
N1 = No of primary turns
N2 = No of secondary turns
Φm = max flux in cone (wb)
Φm = Bm x A
f = Frequency of input(ac) Hz
Average rate of change of flux
= Φm / ¼
= 4 ΦmF volts
Average emf per turn = 4F ΦmV
As Φ varies sinusoidally rms value of induced emf is given as
Form factor = r.m.s value / average value = 1.11
r.m.s value of emf/turn = 1.11 x 4f Φm
= 4.44 f Φm volt
r.m.s value of induced emf in primary winding
= (induced emf/turn) x No of primary turns
E1 = 4.44 fN1 Φm
E1 = 4.44 fN1BmA
r.m.s emf induced in secondary
E2 = 4.44 fN2 Φm
E2 = 4.44 fN2BmA
E1/E2 = N1/N2 = K
K – voltage transformation
(i). If N2 > N1 i.e K > 1 STEP UP TRASFORMER
(II). If N1 > N2 i.e K<1 STEP DOWN TRASFORMER
FOR Ideal Transformer
V1 I1 = V2 I2 = 1/K
Hence, current is inversely proportional to the voltage transformation ratio.
Q1>. A 25 KVA transformer has 500 turns on primary and 50 on secondary. The primary is connected to 2000V, 50 Hz supply. Find full load primary and secondary currents, the secondary emf and max flux in core. Neglect leakage drop and no load primary current.
Sol : K = N2/N1 = 50/500 = 1/10
I1 = 25,000/2000 = 12.5 A
I2 = I1/K = 10 x 12.5 A = 125 A
Emf/turn on primary side = 2000/500 = 4 V
E2 = KE1
E2 = 4 x 50 = 200 v
E1 = 4.44fN1 Φm
2000 = 4.44 x 50 x 500 x Φm
Φm = 18.02 m Wb

The basic transformer and its equivalent circuit both are shown below,
Fig. Equivalent Transformer Circuit
Iµ - magnetising component of current
Iw = working component
R0 – Non- inductive resistance
I0 – No load current
X0 = E1/I0. R0 = E1/Iw
E2/E1 = N2/N1 = K
E’2 = E2/K = E1
V’2 = V2/K
I’2 = K I2
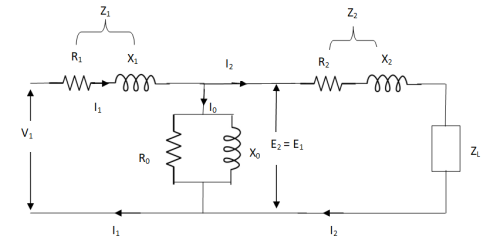
The total equivalent circuit is again given as,

But the above circuit is exact equivalent but harder to solve so, it can be further simplified as,
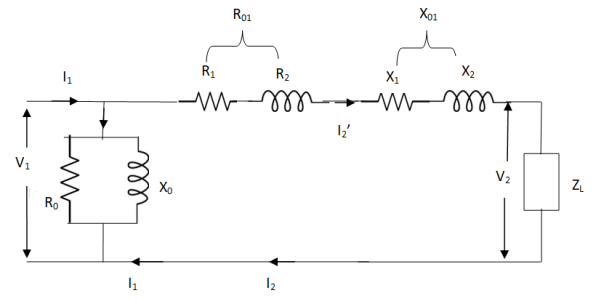
Z = Z1 + Zm || ( Z’2 + Z’L )
= Z1 + Zm(Z’2 + Z’L)/Zm + (Z’2 + Z’L)
Z’2 = R’2 + jX’2
Zm = impedance of exciting circuit
V1 = I1[ Z1 + Zm(Z’2 + Z’L) / Zm + (Z’2 + Z’L) ]
Core or Iron Loss :
This includes both hysteresis loss and eddy current loss. Iron or core loss is found from open circuit test.
Hysteresis Loss(Wh) = nB1.6max f V Watt
Eddy current Loss(We) = P B2max f2 t2 Watt
(2). Copper Loss :
This is due to ohmic resistance of the transformer windings.
Total cu loss = I21 R1 + I22 R2
= I21 R01 + I22 R02
Cu loss α I2
The value of cu loss is found from short-circuit test.
Efficiency of transformer :
Basically efficiency is defined as
n = output/input
But for transformer there are small amount of losses so the improved way to find efficiency is
n = output/output + losses
n = output/output + cu loss + iron loss
Or n = Input – losses/Input
= 1 – Losses/Input
Condition for maximum efficiency :
For n to be maximum dn/dI1 = 0
(Ww) cu loss = I21 R01 or I22 R02
Iron loss = Hysteresis loss + Eddy current loss
= Wn + We = Wi
n = Input – losses/Input
Primary Input = V1I1 Cosφ1
n = V1 I1 Cosφ1 – losses/V1 I1 cos φ1
n = V1 I1 cos φ1 – I21 R01 – Wi / V1I1 cosφ1
= 1 – I1R01/V1cosφ1 – Wi/V1I1cosφ1
Differentiating w.r.t I1 both sides of above equation we have
Dn/dI1 = 0 – R01/V1cosφ1 + Wi/V1I21 Cosφ1
For max value dn/dI1 = 0
R01/V1cosφ1 = Wi/V1I21 cosφ1
Wi = I21 = I21 R01
Hence,
Wi = Wcu
Iron loss = copper loss
The value of output current for maximum efficiency will be
I2 = √Wi/R02
The maximum efficiency can also be given as,
nmax = full load x √ Iron loss / F.L .cu loss
Or
nmax = R’ x full load KVA x pf / R’ x full load KVA x pf + Wi + Wcu x 100
R’ = ratio of actual to full load KVA
Wi = iron loss (KW)
Wcu = copper loss (KW)
Q1). In a 50 KVA, 2200/200 V, 1-φ transformer, the iron and full-load copper losses are 400 W and 450 W respectively. Calculate n at unity power factor on (i). Full load (ii). Half-full load?
Sol. (i). Total loss = 400 + 450 = 850 W
F.L output at unity power factor = 50 x 1
= 50 KVA
n = 50 / 50 + .850 = 50/50.850 = 0.98 = 98%
(ii). Half full load, unity pf
= 50 KVA/2 = 25 KVA
Cu loss = 400 x (1/2)2 = 100 W
Iron loss is same = 450 W
Total loss = 100 + 450 = 550 W
n = 25/25 + 0.55 = 25/25.55 = 0.978 = 97.8 %
Q>. A 40 KVA 440/220 V, 1- φ, 50 Hz transformer has iron loss of 300 W. The cu loss is found to be 100 W when delivering half full-load current. Determine (i) n when delivering full load current at 0.8 lagging pf (ii) the percentage of full-load when the efficiency will be max.
Sol. Full load efficiency at 0.8 pf
= 40 x 0.8/(40 x 0.8) + losses
Full load cu loss = (440/220)2 x 100
= 400 W
Iron loss = 400 + 300
= 700 W
n = 40 x 0.8/(40 x 0.8) + 0.7 = 97.8 %
(ii). KVA for maximum / F.L KVA = √ iron loss / F.L cu loss
= √300/400 = 0.866
(1). OPEN CIRCUIT TEST :
Basically these tests are performed to find the basic parameters of transformers. The open circuit test is performed to determine no-load loss(core loss) and no-load current I0 which is helpful in finding X0 and R0.
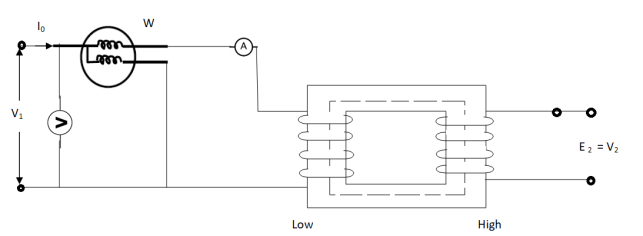
Fig. Open Circuit Test
In this test the high voltage winding is left open and the other is connected to supply.
A wattmeter W, voltmeter V and an Ammeter A are connected to L.V. Winding.
Due to applied voltage in primary, flux is set up in core, and hence normal iron loss occurs. This is recorded in Wattmeter. The current I0 is measured by Ammeter A.
Wattmeter reading represents core loss under no-load condition.
The wattmeter reading will be given as
W = V1 I0 cos φ0
Iµ = I0 Sin φ0
Iw = I0 cos φ0
X0 = V1/Iµ, R0 = V1/Iw
At no load I0 ≈ Iµ
I0 = V1 Y0
Y0 – Exciting Admittance
W = V21 G0
G0 – Exciting conductance
B0 = √ Y20 – G20
B0 – Exciting susceptance
(2) SHORT CIRCUIT TEST :
This test is used to determine
(i). Equivalent Impedance (Z01, Z02), leakage reactance’s (X01 or X02), Total resistance (R01, R02).
(ii). Cu losses are also calculated at full load.
(iii). The regulation of transformer can be determined as Z01, Z02 can be calculated.

Here low voltage is short circuited. And the supply is through high voltage (primary here).
As applied voltage is small, hence the flux φ induced is also small.
As core losses are very small, the wattmeter reading is the cu-loss at full load for whole transformer.
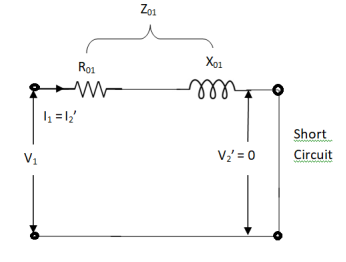
The equivalent circuit is shown below,
Z01 = Vsc/I1
Vsc = voltage to circulate rated load current
W = I21 R01
R01 = W / I21
X01 = √ Z201 – R201
R’2 = R01 – R1
Q1>. The primary and secondary windings of a 30 KVA, 5000/330 V, 1- φ transformer having resistance of 15 Ω and 0.02 Ω. The reactance referred to primary is 34 Ω. Calculate primary voltage required to circulate full-load current when the secondary is S.C. Also calculate the pf?
Sol. K = 330/5000 = 33/500
X01 = 34 Ω
R01 = R1 + R2/K2 = 15 + 0.02(500/33)2 = 19.59 Ω
Z01 = √ R201 – X201
= √ 19.592 + 342
Z01 = 39.23 Ω
F. L I1 = 30,000/5000 = 6A
Vsc = I1 Z01 = 6 x 39.23 = 235.4 V
S.C. Power factor = R01 / Z01 = 19.59/39.23 = 0.5
Q.2). In no-load test of 1- φ transformer, the test data are
Primary voltage = 200 V,
Resistance of primary = 0.6 Ω
Secondary voltage = 100 V
Primary current = 0.6 A
Power input = 30 W
Find (a) Turns ratio (b) Magnetising component of no-load current (c) Working component (d) Iron loss
Sol>. (a). N1/N2 = 200/100 = 1
(b). W = V1 I0 cos φ0
Cos φ0 = 30/200 x 0.6 = 0.25, sin φ0 = 0.97
Iµ = I0 sin φ0 = 0.6 x 0.97 = 0.58 A
©. Iw = I0 Cos φ0 = 0.6 x 0.25 = 0.15 A
(d). Cu loss = I20 R1 = (0.6)2 x 0.6 = 0.216 W
Iron loss = 30 – 0.216 = 29.78 W
Q.3 Obtain the secondary voltage when delivered 10 KW at 0.8 PF.logging . The primary volt be 220v. The 300/600 v 50H2, 1- Transformer has following test results.
Transformer has following test results.
O.C test-:200v, 0.8A 70W-L.V side
S.C test-: 12V,10A 80W-HV side
Soln:- O.C TEST
W=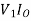 COS
COS 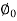
70=200*0.8*Cos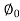
Cos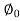 = 0.436
= 0.436
Sin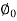 =0.899
=0.899
 =
=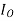 COS
COS =0.8*0.436=0.35A
=0.8*0.436=0.35A
I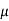 =
=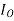 sin
sin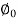 = 0.8*0.899=0.72A
= 0.8*0.899=0.72A
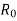 =
=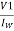 =
=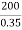 =571.4
=571.4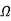
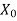 =
=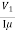 =
= =277.8𝛺
=277.8𝛺
S.C TEST-:
 =
= =
=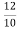 =1.2A
=1.2A
K=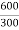 =2
=2
Z01= =
=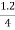 =0.3
=0.3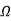
I22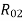 =W
=W
RO2=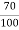 =0.7
=0.7
R01=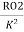 =
=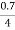 =0.175𝛺
=0.175𝛺
X01=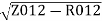
= 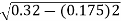
X01 = 0.244
Output KVA = =12.5
=12.5
I2=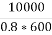 = 20.83A
= 20.83A
Z02=1.2A R02=0.7𝛺
X02=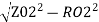 =0.975𝛺
=0.975𝛺
Total transformer drop refereed to secondary
= I2 (RO2COS + X02Sin
+ X02Sin )
)
= 20.83(0.7*0.8+0.975*0.6)
= 23.85v
 = 600 - 23.85=576.15v
= 600 - 23.85=576.15v