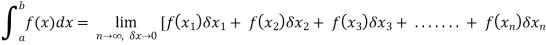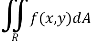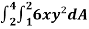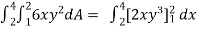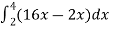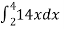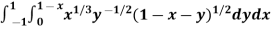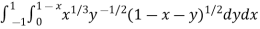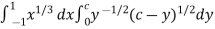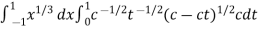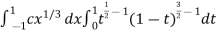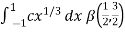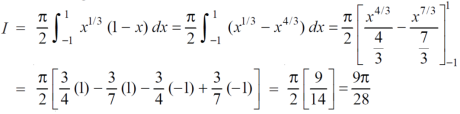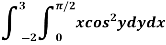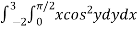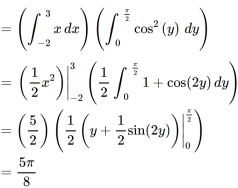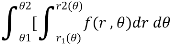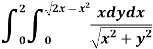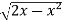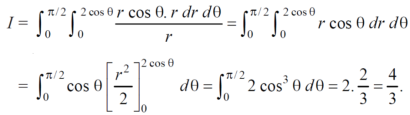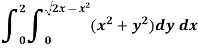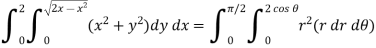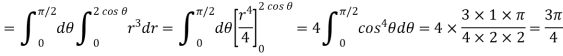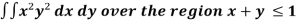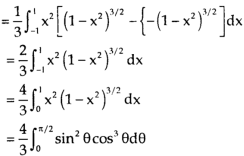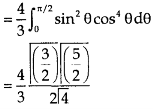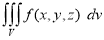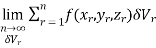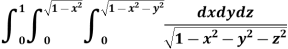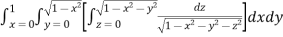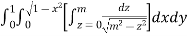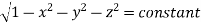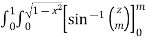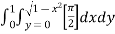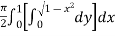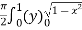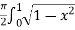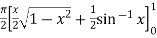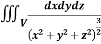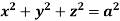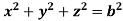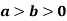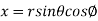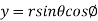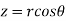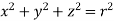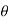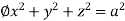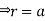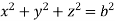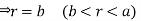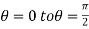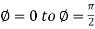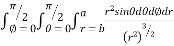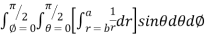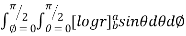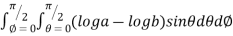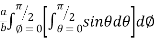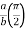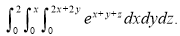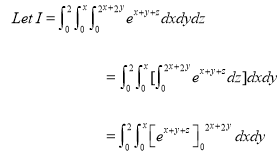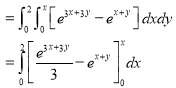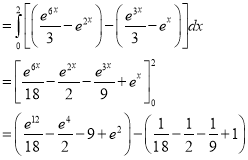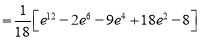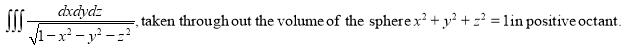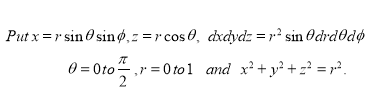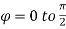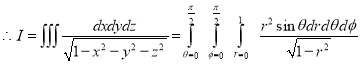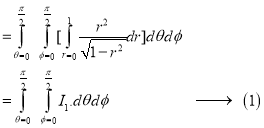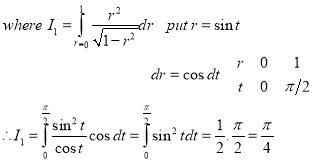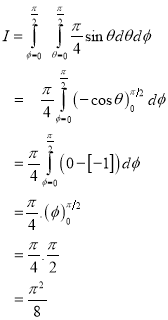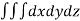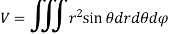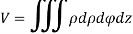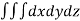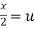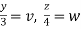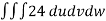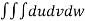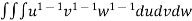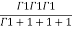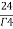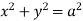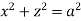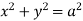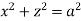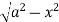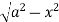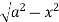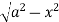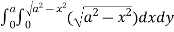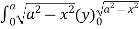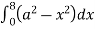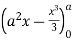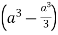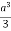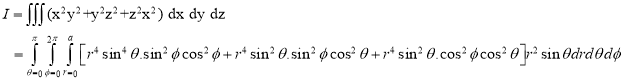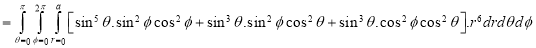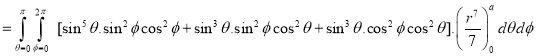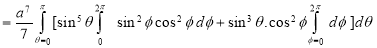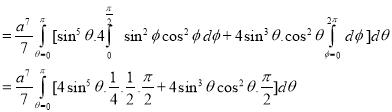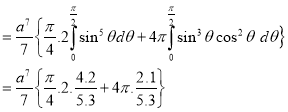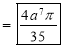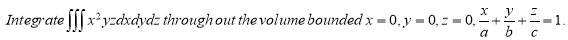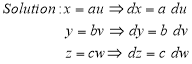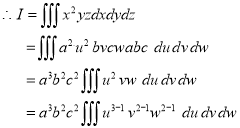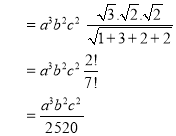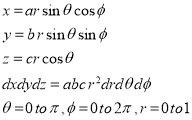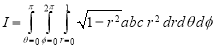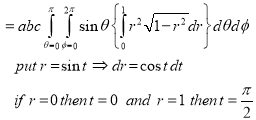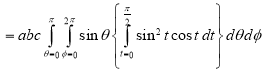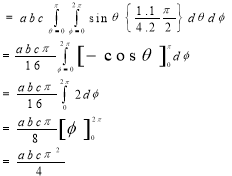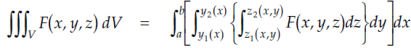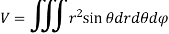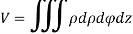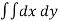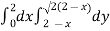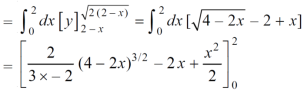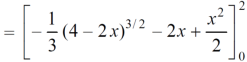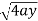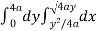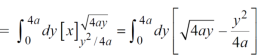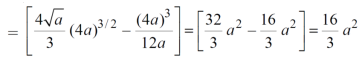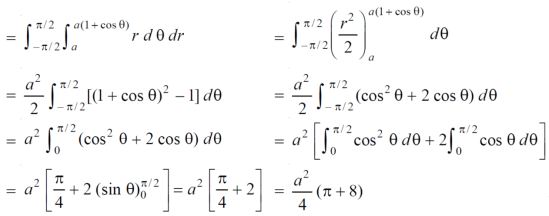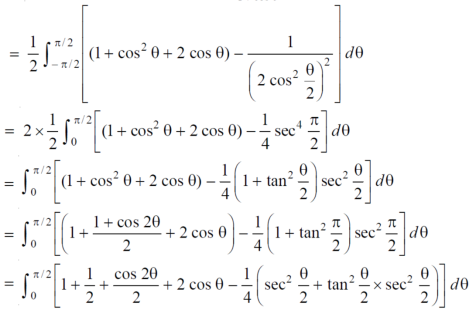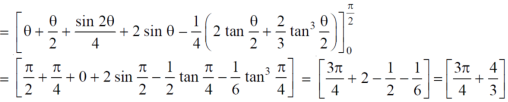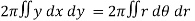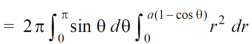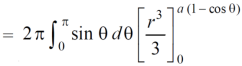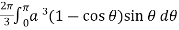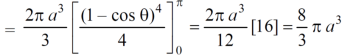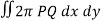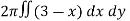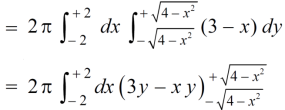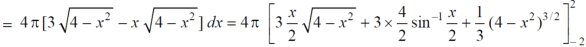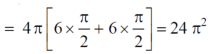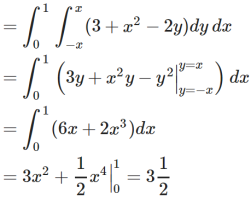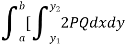UNIT-5
Multivariable Calculus (Integration)
Double integral –
Before studying about multiple integrals, first let’s go through the definition of definition of definite integrals for function of single variable.
As we know, the integral
Where is belongs to the limit a ≤ x ≤ b
|
This integral can be written as follows-
|
Now suppose we have a function f (x, y) of two variables x and y in two-dimensional finite region Rin XY-plane.
Then the double integration over region R can be evaluated by two successive integration
|
Evaluation of double integrals-
If A is described as Then,
|
Let do some examples to understand more about double integration-
Example-1: Evaluate Sol. Let , I = = = = = 84 sq. unit. Which is the required area, |
Example-2: Evaluate Sol. Let us suppose the integral is I, I = Put c = 1 – x in I, we get I = Suppose, y = ct Then dy = c now we get, I = I = I = I = I = As we know that by beta function,
Which gives,
Now put the value of c, we get
|
Example-3: Evaluate the following double integral,
|
Sol. Let, I = On solving the integral, we get
|
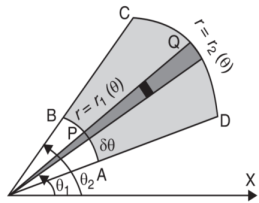
Double integration in polar coordination -
In polar coordinates, we need to evaluate
|
Over the region bounded by θ1 and θ2.
And the curves r1(θ) and r2(θ)
|
Example-1: Evaluate the following by changing to polar coordinates,
|
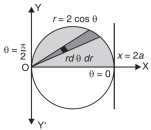
Sol. In this problem, the limits for y are 0 to Suppose, y = squaring both sides, y² = 2x - x² x² + y² = 2x but in polar coordinates, we have, r² = 2r cosθ r = 2 cosθ from the region of integration, r lies from 0 to 2 cosθ and θ varies from 0 to π / 2. As we know in case of polar coordinates, Replace x by r cosθ and y by r sinθ, dy dx by r drdθ, We get,
|
Example-2: Evaluate the following integral by converting into polar coordinates.
|
Sol. Here limits of y, y = y² = 2x - x² x² + y² = 2x x² + y² - 2x = 0 ………………(1)
Eq. (1) represent a circle whose radius is 1 and Centre is ( 1, 0) Lower limit of y is zero. Region of integration in upper half circle, First we will convert into polar coordinates, By putting x by r cos θ and y by r sinθ , dy dx by r drdθ,
limits of ‘r’ are 0 to 2 cosθ and limits of θ are from 0 to π / 2.
|
Example-3: Evaluate |
Sol. Let the integral, I = =
Put x = sinθ
= π / 24 ans. |
Triple integrals
Definition: Let f (x, y, z) be a function which is continuous at every point of the finite region (Volume V) of three-dimensional space. Divide the region V into n sub regions of respective volumes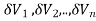 . Let (
. Let ( ) be a point in the
) be a point in the 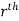 sub region then the sum:
sub region then the sum:
is called triple integration of f (x, y, z) over the region V provided limit on R.H.S of above Equation exists.
|
Example-1: Evaluate
|
Solution: Let I = = (Assuming m = = = = = = = = I = |
Example-2: Evaluate |
Solution: It is convenient to transform the triple integral into spherical polar co-ordinate by putting
For the positive octant, r varies from r =b to r =a , I= = 8 =8 =8 =8 =8 log = 8 log I= 8 log I = 4 log |
Example-3: Evaluate
|
Solution:-
|
Ex.4: Evaluate-
|
Solution:-
|
NOTES: The volume of solid is given by Volume = In Spherical polar system
In cylindrical polar system
|
Ex.1: Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane
|
Solution: Volume = Put
From equation (1) we have V = =24 =24 =24 = Volume =4 |
Ex.2: Find volume common to the cylinders |
Solution: For given cylinders,
Z varies from Z=- Y varies from y= - x varies from x= -a to x = a By symmetry, Required volume= 8 (volume in the first octant) =8 =8 = 8 =8 =8 =8 Volume = 16 |
Ex.3: Evaluate 1. |
Solution:-
|
Ex.4: |
|
Ex.5: Evaluate |
Solution:- Put
|
Volume = 3. In Spherical polar system
4. In cylindrical polar system
|
Area in Cartesian coordinates-
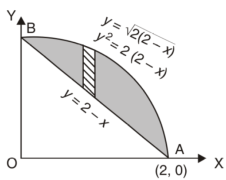
Example-1: Find the area enclosed by two curves using double integration. y = 2 – x and y² = 2 (2 – x) |
Sol. Let, y = 2 – x ………………..(1) and y² = 2 (2 – x) ………………..(2) on solving eq. (1) and (2) we get the intersection points (2,0) and (0,2) , we know that, Area =
Here we will find the area as below, Area =
Which gives, = ( - 4 + 4 /2 ) + 8 / 3 = 2 / 3. |
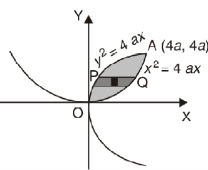
Example-2: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay. Sol. Let, y² = 4ax ………………..(1) and x² = 4ay…………………..(2) then if we solve these equations , we get the values of points where these two curves intersect
x varies from y²/4a to now using the concept of double integral, Area =
|
Area in polar coordinates-
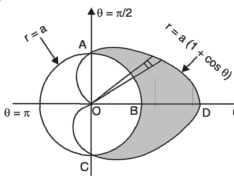
Example-3: Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration. |
Sol. We have, r = a(1+cosθ) …………………….(1) and r = a ……………………………….(2) on solving these equations by eliminating r , we get a(1+cosθ) = a (1+cosθ) = 1 cosθ = 0 here a θ varies from – π/2 to π/2 limit of r will be a and 1+cosθ)
Which is the required area.
|
Example-4: Find the are lying inside a cardioid r = 1 + cosθ and outside the parabola r(1 + cosθ) = 1. |
Sol. Let, r = 1 + cosθ ……………………..(1) r(1 + cosθ) = 1……………………..(2) solving these equations, we get (1 + cosθ )(1 + cosθ ) = 1 (1 + cosθ )² = 1 1 + cosθ = 1 cosθ = 0 θ = ±π / 2 so that, limits of ‘r’ are, 1 + cosθ and 1 / 1 + cosθ The area can be founded as below,
|
Double integrals as volumes
Suppose we have a curve y = f(x) is revolved about an axis, then a solid is generated, now we need to find out the volume of the solid generated.
|
Q
The formula for volume of the solid generated about x-axis,
|
Example-1: Calculate the volume generated by the revolution of a cardioid, r = a ( 1 – cosθ) about its axis |
Sol. Here, r = a ( 1 – cosθ) Volume =
=
which is the volume of generated by cardioid. |
Example-2: Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3. |
Sol. We know that, Volume = Here , PQ = 3 – x, =
The volume is 24π². |
Example-3: Calculate the volume under the surface z = 3 + x² - 2y over the region R defined as 0≤ x ≤ 1 and -x ≤ y ≤ x |
Sol. The is a double integral of z = 3 + x² - 2y over the region R. Volume will be,
|
Key takeaways-
The formula for volume of the solid generated about x-axis,
|
References
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- BV ramana, higher engineering mathematics