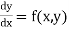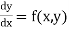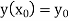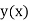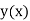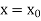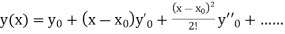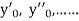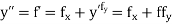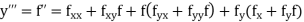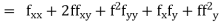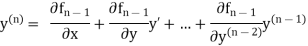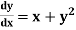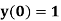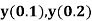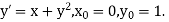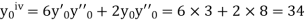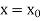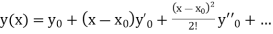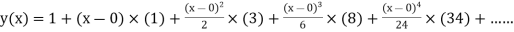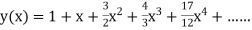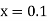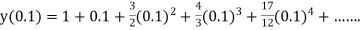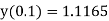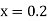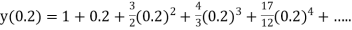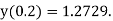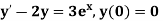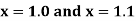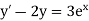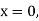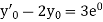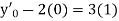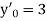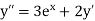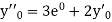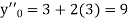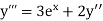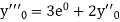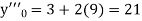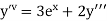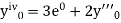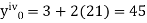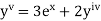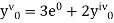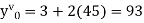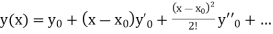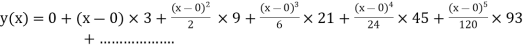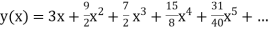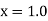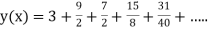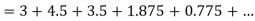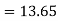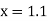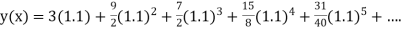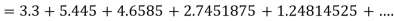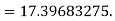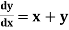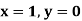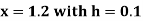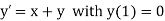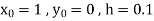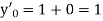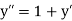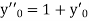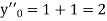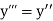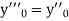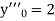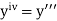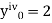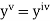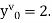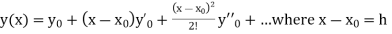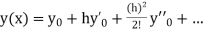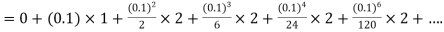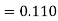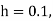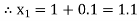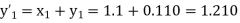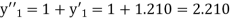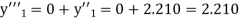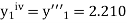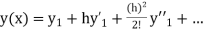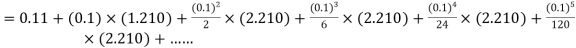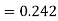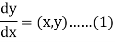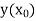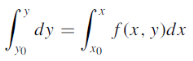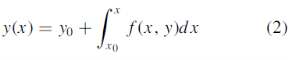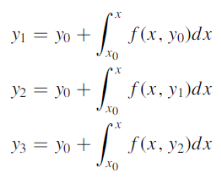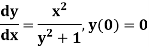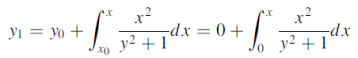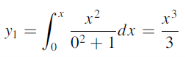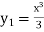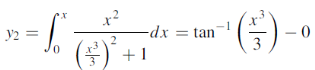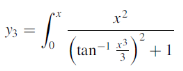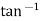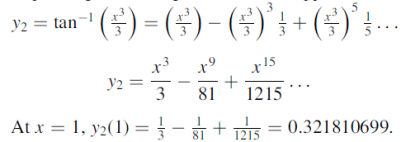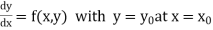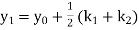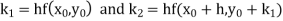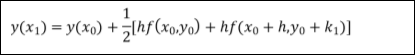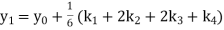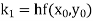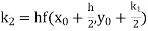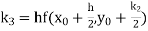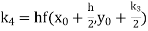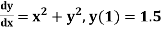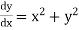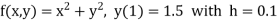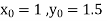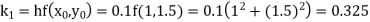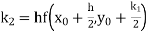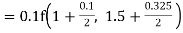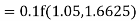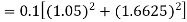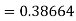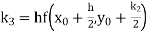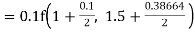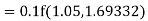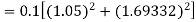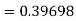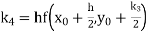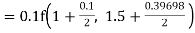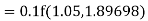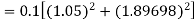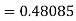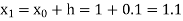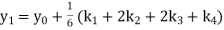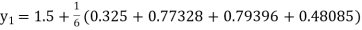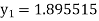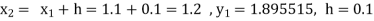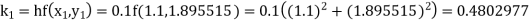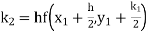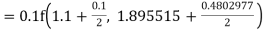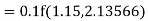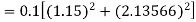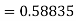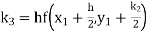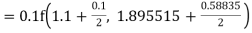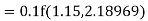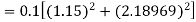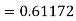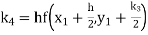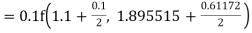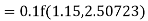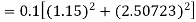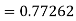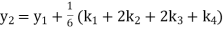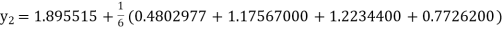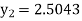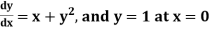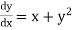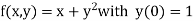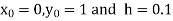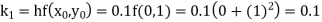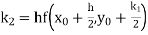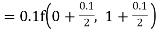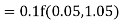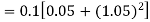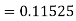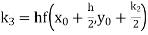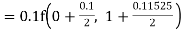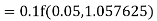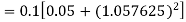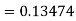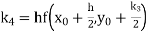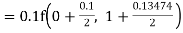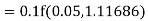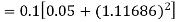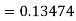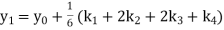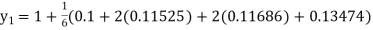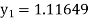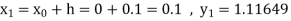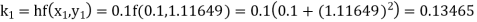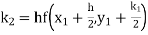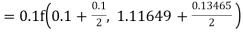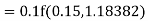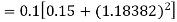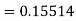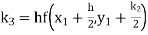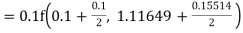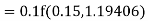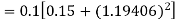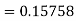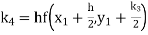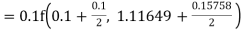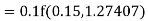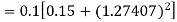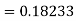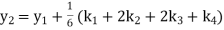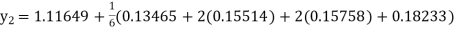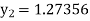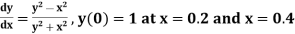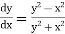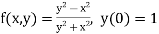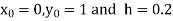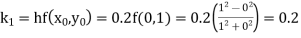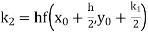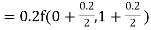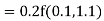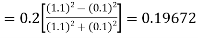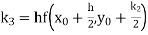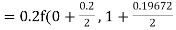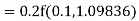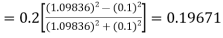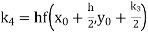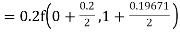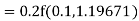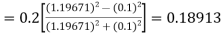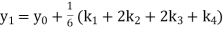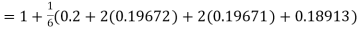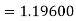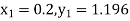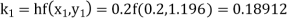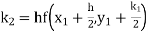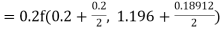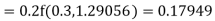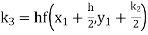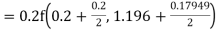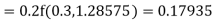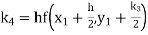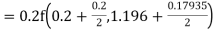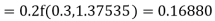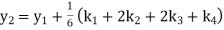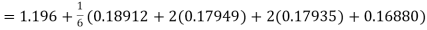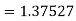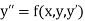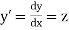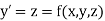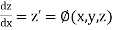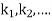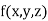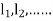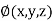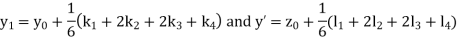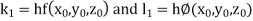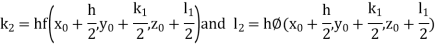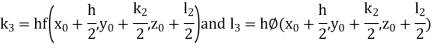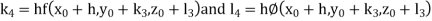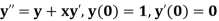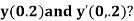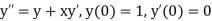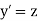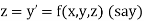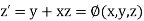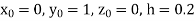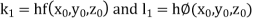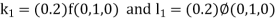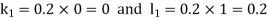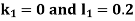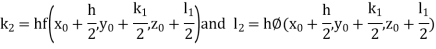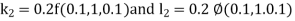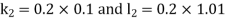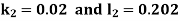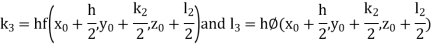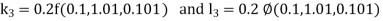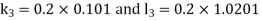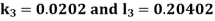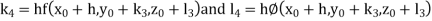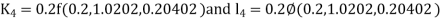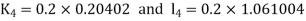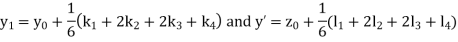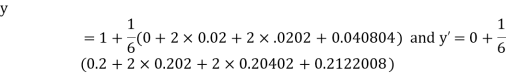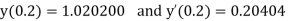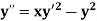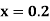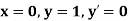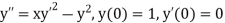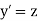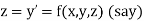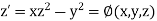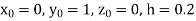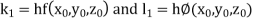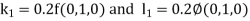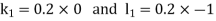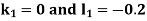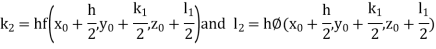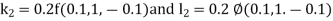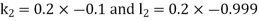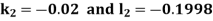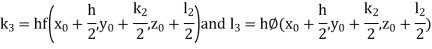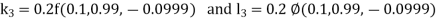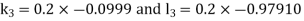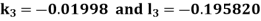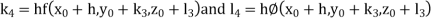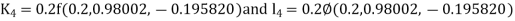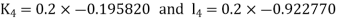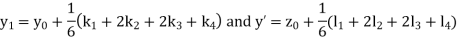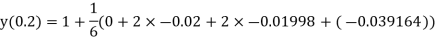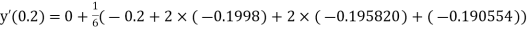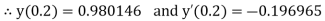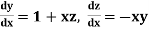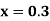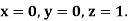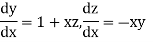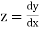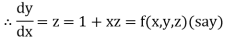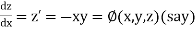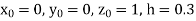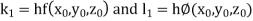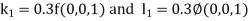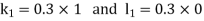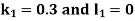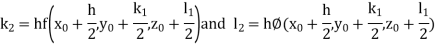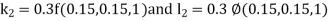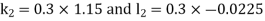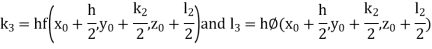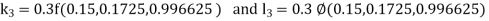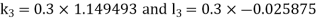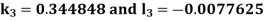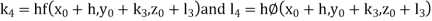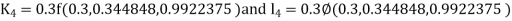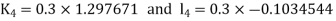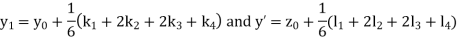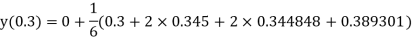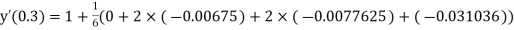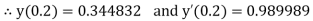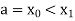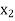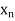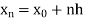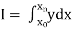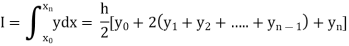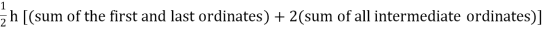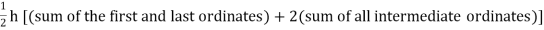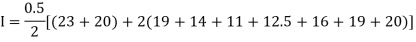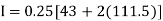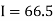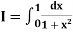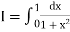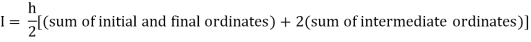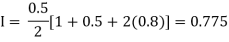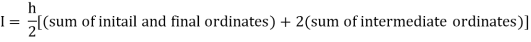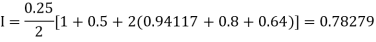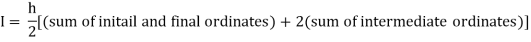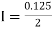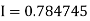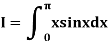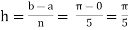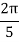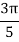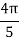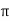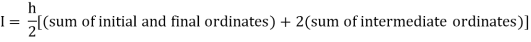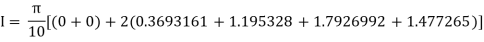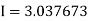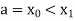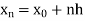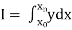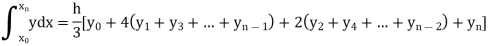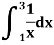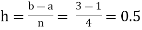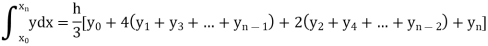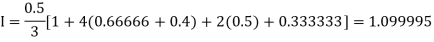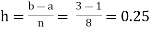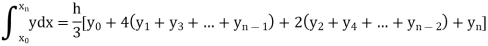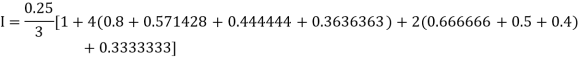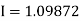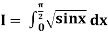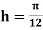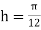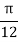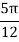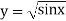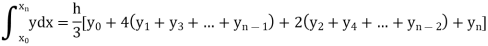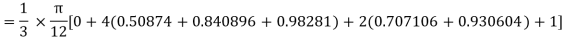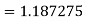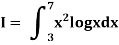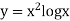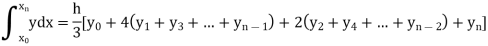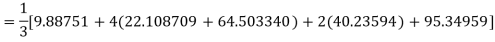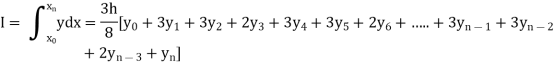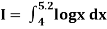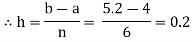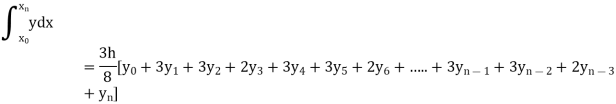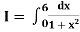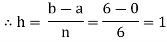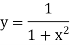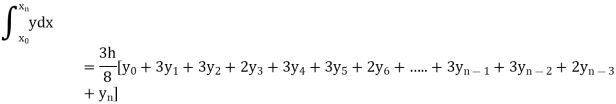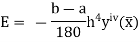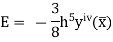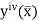UNIT-4
Numerical methods
The general first order differential equation
|
With the initial condition 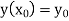 …(2)
…(2)
In general, the solution of first order differential equation in one of the two forms:
a) A series for y in terms of power of x, from which the value of y can be obtained by direct solution.
b) A set of tabulated values of x and y.
The case (a) is solved by Taylor’s Series or Picard method whereas case (b) is solved by Euler’s, Runge Kutta Methods etc.
Taylor’s Series Method:
The general first order differential equation
With the initial condition Let
If the values of
And other higher derivatives of y. The method can easily be extended to simultaneous and higher –order differential equations. In general,
|
Putting 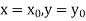 in these above results, we can obtain the values of
in these above results, we can obtain the values of 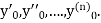 finally, we substitute these values of
finally, we substitute these values of 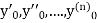 in equation (2) and obtain the approximate value of y; i.e. the solutions of (1).
in equation (2) and obtain the approximate value of y; i.e. the solutions of (1).
Example1: Solve |
Here Differentiating, we get The Taylor’s series at At At |
Example2: Using Taylor’s series method, find the solution of |
Here At Differentiating, we get The Taylor’s series at At At
|
Example3: Solve
|
Here We have Differentiating, we get The Taylor’s series at Or Here The Taylor’s series |
Picard’s method of successive approximation-
The P.I. of the initial value problem having an ODE-
With initial condition
Or
|
In the Picard’s method, the first approximation y1 is obtained by replacing y in f (x, y) in RHS of (2) by y0 and then evaluating the integral (which is now a function of x) w.r.t x. The second approximation y2 is then obtained by replacing y in f (x, y) of RHS of (2) by y1 and integrating w.r.t x. Successive approximations are obtained similarly. In practice, Picard’s method is restricted to a limited class of problems in which the integral in RHS of (2) can be evaluated.
So that-
………………………….. ……………………………. |
Example: Obtain the Picard’s second approximation for the initial value problem-
Find y(1). |
Sol. The first approximation-
Replace y by
Replace y by
Third approximation-
Here we find that the integration is very difficult. Now expanding We get-
|
This method is more accurate than Euler’s method.
Consider the differential equation of first order
Let A second order Runge Kutta formula Where
A fourth order Runge Kutta formula: Where |
Example1: Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that |
Given equation Here Also By Runge Kutta formula for first interval Again A fourth order Runge Kutta formula: To find y at A fourth order Runge Kutta formula: |
Example2: Apply Runge Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if |
Given equation Here Also By Runge Kutta formula for first interval A fourth order Runge Kutta formula: Again A fourth order Runge Kutta formula: |
Example3: Using Runge Kutta method of fourth order, solve |
Given equation Here Also By Runge Kutta formula for first interval A fourth order Runge Kutta formula: Hence at x = 0.2 then y = 1.196 To find the value of y at x=0.4. In this case A fourth order Runge Kutta formula: Hence at x = 0.4 then y=1.37527 |
Solution of Second order ODE using 4th order Runge-Kutta method:
The second order differential equation
Let
Then This can be solved as we discuss above by Runge Kutta Method. Here A fourth order Runge Kutta formula:
Where
|
Example1: Using Runge Kutta method of order four , solve |
Given second order differential equation is
Let Or
Or By Runge Kutta Method we have
A fourth order Runge Kutta formula:
|
Example2: Using Runge Kutta method, solve
|
Given second order differential equation is
Let Or
Or By Runge-Kutta Method we have
A fourth order Runge Kutta formula:
And
|
Example3: Solve the differential equations
Using four order Runge Kutta method with initial conditions |
Given differential equation are
Let
And Also By Runge Kutta Method we have
A fourth order Runge Kutta formula:
And
|
Numerical integration is a process of evaluating or obtaining a definite integral 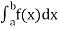 from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature.
from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature.
Trapezoidal Method:
Let the interval [a, b] be divided into ‘n’ equal intervals such
that Here To find the value of |
Setting n=1, we get
Or I = |
The above is known as Trapezoidal method.
Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x), is replaced by n straight lines with the points 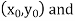 (
(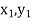 );(
);(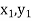 ) and (
) and (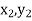 );…….;(
);…….;(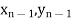 ) and (
) and (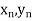 ).
).
The area bounded by the curve y=f(x), the ordinates 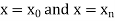 ,and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
,and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below: (0, 23), (0.5, 19), (1.0, 14), (1.5, 11), (2.0, 12.5), (2.5, 16), (3.0, 19), (3.5, 20), (4.0, 20). Estimate the area bounded by the curve, the x axis and the extreme ordinates. |
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method Area of curve bounded on x axis =
| ||||||||||||||||||||||||||||||||||||||||
Example2: Compute the value of Using the trapezoidal rule with h=0.5, 0.25 and 0.125. | ||||||||||||||||||||||||||||||||||||||||
Here For h=0.5, we construct the data table:
By Trapezoidal rule
For h=0.25, we construct the data table:
By Trapezoidal rule
For h = 0.125, we construct the data table:
By Trapezoidal rule
| ||||||||||||||||||||||||||||||||||||||||
Example3: Evaluate, using trapezoidal rule with five ordinates
Here | ||||||||||||||||||||||||||||||||||||||||
We construct the data table:
|
Simpson’s Rule:
Let the interval [a, b] be divided into ‘n’ equal intervals such that Here To find the value of Setting n = 2,
|
Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Note: In this rule third and higher differences are neglected so f(x) is a polynomial of degree 2.
Example1: Estimate the value of the integral
by Simpson’s rule with 4 strips and 8 strips respectively | ||||||||||||||||||||||||||||||||
For n=4, we have We construct the data table:
By Simpson’s Rule
For n = 8, we have
By Simpson’s Rule
| ||||||||||||||||||||||||||||||||
Example2: Evaluate Using Simpson’s 1/3 rule with | ||||||||||||||||||||||||||||||||
For
By Simpson’s Rule
| ||||||||||||||||||||||||||||||||
Example3:Using Simpson’s 1/3 rule with h = 1, evaluate
| ||||||||||||||||||||||||||||||||
For h = 1, we construct the data table:
By Simpson’s Rule
= 177.3853 |
Simpson’s 3/8 rule
Let the interval [a, b] be divided into n equal intervals such that 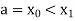 <
<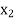 <….<
<….<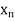 =b.
=b.
Here 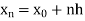 .
.
To find the value of 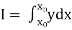 .
.
Setting n=3 , we get
|
Is known as Simpson’s 3/8 rule which is not as accurate as Simpson’s rule.
Note: In this rule the fourth and higher differences are neglected and so f(x) is a polynomial of degree 3.
Example: Evaluate | ||||||||||||||||
Let us divide the range of the interval [4, 5.2] into six equal parts.
For h=0.2, we construct the data table:
By Simpson’s 3/8 rule
= 1.8278475 | ||||||||||||||||
Example2: Evaluate | ||||||||||||||||
Let us divide the range of the interval [0,6] into six equal parts.
For h=1, we construct the data table:
By Simpson’s 3/8 rule
=1.3571 |
Error in Integration-
Error in Trapezoidal method
The total error in trapezoidal method is given by
Let
|
Error in Simpson’s Rule
The error in the Simpson’s rule is given by
|
Where 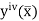 is the largest value of the fourth derivative of y(x).
is the largest value of the fourth derivative of y(x).
Error in Simpson’s 3/8 Rule
The error in this rule is given by
Where |
References
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- BV ramana, higher engineering mathematics