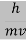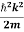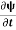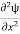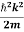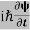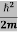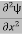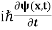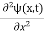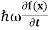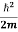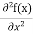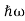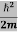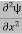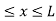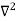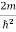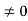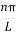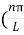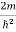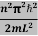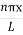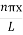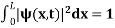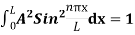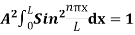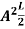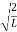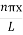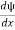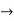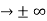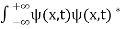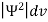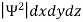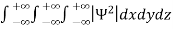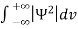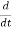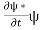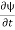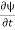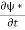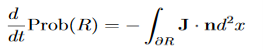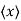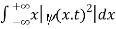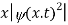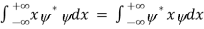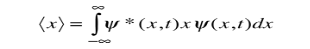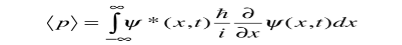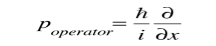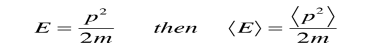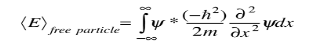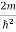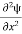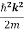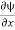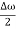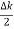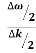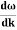UNIT 3
QUANTUM MECHANICS AND NANOTECHNOLOGY FOR ENGINEERS
The term "quantum mechanics" was first coined by Max Born in 1924.
Quantum mechanics is the branch of physics dealing with the behaviour of matter and light on the atomic and subatomic level. . It attempts to describe and account for the properties of molecules and atoms and their constituents—electrons, protons, neutrons, and other more particles such as quarks and gluons.
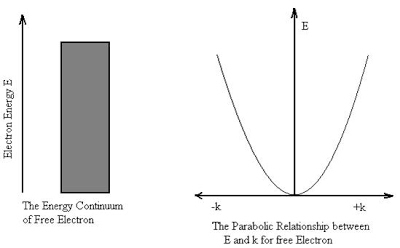
At the scale of atoms and electrons, many of the equations of classical mechanics which describe how things move at everyday sizes and speeds cease to be useful.
In classical mechanics objects exist in a specific place at a specific time. However, in quantum mechanics, objects instead exist in a haze of probability they have a certain chance of being at point A another chance of being at point B and so on. It results some very strange conclusions about the physical world.
At the turn of the twentieth century, however, classical physics not able to explain some of the phenomena.
Relativistic domain: Einstein’s 1905 theory of relativity showed that the validity of
Newtonian mechanics ceases at very high speeds i.e. Speeds comparable to that of light.
Microscopic domain: As soon as new experimental techniques were developed to the point of searching atomic and subatomic structures, it turned out that classical physics fails miserably in providing the proper explanation for several newly discovered phenomena. It thus became evident that the validity of classical physics ceases at the microscopic level and that new concept had needed to describe.
The classical physics fails to explain several microscopic phenomena such as blackbody radiation, the photoelectric effect, atomic stability and atomic spectroscopy
In 1900 Max Planck introduced the concept of the quantum of energy. He successfully explained the phenomenon of blackbody radiation .He introduced the concept of discrete or quantized Energy. He also explained that the energy exchange between an electromagnetic wave of frequency ν and matter occurs only in integer multiples of hν, which he called the energy of a quantum, where h is called Planck’s constant.
In 1905 Einstein provided a powerful consolidation to Planck’s quantum concept. In trying to understand the photoelectric effect, Einstein recognized that Planck’s idea of the quantization of the electromagnetic waves must be valid for light as well.
So, He Gave light itself is made of discrete bits of energy or tiny particles, called photons, each of energy hν, ν being the frequency of the light. The introduction of the photon concept enabled Einstein to give an elegantly accurate explanation to the photoelectric problem.
Bohr introduced in 1913 his model of the hydrogen atom. He explained that atoms can be found only in discrete states of energy and the emission or absorption of radiation by atoms, takes place only in discrete amounts of hν. This successfully explained to problems such as atomic stability and atomic spectroscopy
Then in 1923 Compton made an important discovery of scattering X-rays with electrons, he confirmed that the X-ray photons behave like particles with momenta hν/c, ν is the frequency of the X-rays.
Planck, Einstein, Bohr, and Compton gave the theoretical and experimental confirmation for the particle aspect of wave that means that waves exhibit particle behaviour at the microscopic scale.
Some of the most prominent scientists to subsequently contribute in the mid-1920s to what is now called the "new quantum mechanics" or "new physics" were Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, and Erwin Schrödinger.
Through a century of experimentation and applied science, quantum mechanical theory has proven to be very successful and practical.
Historically, there were two independent formulations of quantum mechanics. The first formulation, called matrix mechanics, was developed by Heisenberg (1925) to describe atomic structure starting from the observed spectral lines.
The second formulation, called wave mechanics, was due to Schrödinger (1926).
It is a generalization of the de Broglie postulate. This method describes the dynamics of microscopic matter by means of a wave equation, called the Schrodinger equation.
Dirac derived in 1928 an equation which describes the motion of electrons. This equation, known as Dirac’s equation, predicted the existence of an antiparticle.
In short, quantum mechanics is the founding basis of all modern physics: solid state, molecular, atomic, nuclear, and particle physics, optics, thermodynamics, statistical mechanics, and so on. Not only that, it is also considered to be the foundation of chemistry and biology.
As we know in the Photoelectric Effect, the Compton Effect, and the pair production effect—radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal.
In 1923, the French physicist Louis Victor de Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
All material particles should also display dual wave–particle behaviour. That is, the wave–particle duality present in light must also occur in matter.
So, starting from the momentum of a photon p = hν/c = h/λ.
We can generalize this relation to any material particle with nonzero rest mass. Each material particle of momentum 
behaves as a group of waves (matter waves) whose wavelength λ and wave vector 
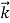are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
λ = |
Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation.
λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment.
However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c.
Therefore
= 
= λ
Example: What is the frequency of a photon with energy of 4.5 eV?
Solution:
E = (4.5 eV) x (1.60 x 10-19 J/eV) = 7.2 x 10-19 J
E = hf
h = 6.63 x 10-34 J x s
f = E / h = (7.2 x 10-19 J) / (6.63 x 10-34 J x s)
f = 1.1 x 1015 Hz
De Broglie’s Hypothesis: Matter Waves
Matter waves: According to De-Broglie, a wave is associated with each moving particle which is called matter waves.
As we know in the photoelectric effect, the Compton Effect, and the pair production effect radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal:
all material particles should also display a dual wave–particle behaviour.
That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p = h ν /c = h/λ, we can generalize this relation to any material particle with nonzero rest mass: each material particle of momentum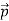 
behaves as a group of waves (matter waves) whose wavelength λ and wave vector
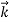are governed by the speed and mass of the particle.
λ = 
= 
Wave has wavelength λ here h is Planck's constant and p is the momentum of the moving particle.
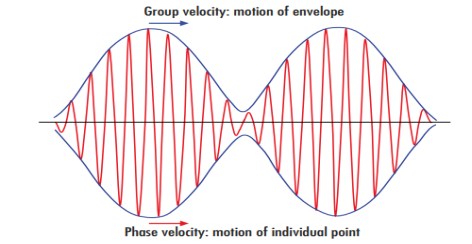
We have seen that microscopic particles, such as electrons, display wave behaviour. What about macroscopic objects? Do they also display wave features? They surely do. Although macroscopic material particles display wave properties, the corresponding wavelengths are too small to detect; being very massive, macroscopic objects have extremely small wavelengths.
At the microscopic level, however, the waves associated with material particles are of the same size or exceed the size of the system. Microscopic particles therefore exhibit clearly noticeable wave-like aspects.
The general rule is: whenever the de Broglie wavelength of an object is in the range of, or exceeds, its size, the wave nature of the object is detectable and hence cannot be neglected.
But if its de Broglie wavelength is much too small compared to its size, the wave behaviour of this object is undetectable.
For a quantitative illustration of this general rule, let us calculate in the following example the wavelengths corresponding to two particles, one microscopic (electron) and the other macroscopic (ball).
Example: What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?
Solution:
(a)For the electron:
Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s.
Then, momentum
p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s)
p = 4.92 × 10–24 kg m/s
de Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s
λ= 0.135 nm
(b)For the ball:
Mass m’ = 0.150 kg,
Speed v ’= 30.0 m/s.
Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s)
p’= 4.50 kg m/s
de Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m
The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement.
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So We have
E= K+V = By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk. Using this equation (1) for the energy will become ℏω =
A wave with frequency ω and wave number k can be written as usual as ψ(x, t) =Aei(kx−ωt) ……….. (3)
the above equation is for one dimensional and for three dimensional we can write it as ψ(r, t) =Aei(k·r−ωt) ……….. (4) But here we will stick to one dimension only.
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain ℏ(ωψ) = This is the time-dependent Schrodinger equation. If we put the x and t in above equation then equation (7) takes the form as given below
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
We already know that E=
Eψ = -
This is called the time-independent Schrodinger equation. |
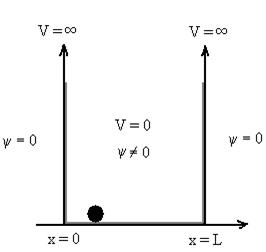
Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically. The potential function is expressed as V= 0 for 0 V=
1 Figure: Particle in deep potential well The probability of finding the particle outside the well is zero (i.e. Ѱ =0) Inside the well, the Schrödinger wave equation is written as
Substituting
writing the SWE for 1-D we get
The general equation of above equation may be expressed as ψ = Asin (kx + ϕ) …………….(5) Where A and ϕ are constants to be determined by boundary conditions Condition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5) 0 = Asin kL As A k = where n= 1,2,3,4……… Substituting the value of k from (7) to (3)
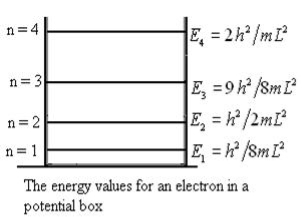
This gives energy of level En = It is clear that the energy values of the particle in well are discrete not continuous.
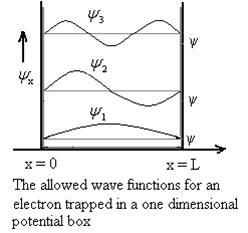
2 Figure: Using (6) and (7) equation (5) becomes, the corresponding wave functions will be ψ = ψn = Asin The probability density |ψ(x,t)|2 = ψ ψ* |ψ(x,t)|2 = A2sin2 The probability density is zero at x = 0 and x = L. since the particle is always within the well
A = Substituting A in equation (9) we get ψ = ψn = The above equation (12) is normalized wave function or Eigen function belonging to energy value En
3 Figure: Wave function for Particle |
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as ψ(x, y, z, t) = a + ib and its complex conjugate as ψ*(x, y, z, t) = a – ib. The product of wave function and its complex conjugate is ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2 a2 + b2 is a real quantity.
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
Only wave function with all these properties can yield physically meaningful result.
Physical significance of wave function
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation. All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics. |
It is not possible to measure all properties of a quantum system precisely. Max Born suggested that the wave function was related to the probability that an observable has a specific value. In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2’. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’ . Thus Ψ2 is a measure of particle density. According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dxdydz) is given by
Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space. i.e.
Or This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function. The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x. |
Let R be some region in space. (Notation: the boundary of R—that is, the surface surrounding R—is often denoted ∂R.) Suppose a particle has a wave function ψ(x,t). We are interested in the probability of finding the particle in the region R: Prob(R) =∫ R|ψ|2d3x Since there is some chance of the particle moving into or out of R, this probability can change in time. Its time derivative is (since|ψ|2=ψ∗ψ).
Now use the Schrodinger equation and its complex conjugate:
Solve for
Check the last equality in equation (3)—do the derivatives!) Then by Stokes theorem (orGreen’s theorem), equation (3) becomes
(Depending on the place you learned this, you may have seen the last term written instead as−∫ J·dA or −∫ J·dS.) Equation (5) should look familiar from E&M: it’s the same form as the equation for charge conservation. It says that the probability I R can change only by an amount equal to the flux of the “probability current ”J through the surface surrounding R. The current J therefore describes the flow of probability, the nearest thing we have in quantum mechanics to a description of the motion of a particle. |
We are looking for expectation values of position and momentum knowing the state of the particle, i.e., the wave function ψ(x,t). Position expectation:
What exactly does this mean? It does not mean that if one measures the position of one particle over and over again, the average of the results will be given by On the contrary, the first measurement (whose outcome is indeterminate) will On the contrary, the first measurement (whose outcome is indeterminate) will collapse the wave function to a spike at the value actually obtained, and the subsequent measurements (if they're performed quickly) will simply repeat that same result. Rather, <x> is the average of measurements performed on particles all in the state ψ, which means that either you must find some way of returning the particle to its original state after each measurement, or else you prepare a whole ensemble of particles, each in the same state ψ, and measure the positions of all of them: <x> is the average of these results. The position expectation may also be written as:
To relate a quantum mechanical calculation to something you can observe in the laboratory, the "expectation value" of the measurable parameter is calculated. For the position x, the expectation value is defined as
This integral can be interpreted as the average value of x that we would expect to obtain from a large number of measurements. While the expectation value of a function of position has the appearance of an average of the function, the expectation value of momentum involves the representation of momentum as a quantum mechanical operator.
where
is the operator for the x component of momentum. Since the energy of a free particle is given by
and the expectation value for energy becomes
for a particle in one dimension. In general, the expectation value for any observable quantity is found by putting the quantum mechanical operator for that observable in the integral of the wavefunction over space:
|
According to classical physics, given the initial conditions and the forces acting on a system, the future behaviour (unique path) of this physical system can be determined exactly. That is, if the initial coordinates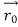
, velocity 
, and all the forces acting on the particle are known, the position 
, and velocity 
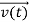are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.
Does this hold for the microphysical world?
Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle.
In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
|
This principle indicates that, although it is possible to measure the momentum or position of a particle accurately, it is not possible to measure these two observables simultaneously to an arbitrary accuracy. That is, we cannot localize a microscopic particle without giving to it a rather large momentum.
We cannot measure the position without disturbing it; there is no way to carry out such a measurement passively as it is bound to change the momentum.
To understand this, consider measuring the position of a macroscopic object (you can consider a car) and the position of a microscopic system (you can consider an electron in an atom). On the one hand, to locate the position of a macroscopic object, you need simply to observe it; the light that strikes it and gets reflected to the detector (your eyes or a measuring device) can in no measurable way affect the motion of the object.
On the other hand, to measure the position of an electron in an atom, you must use radiation of very short wavelength (the size of the atom). The energy of this radiation is high enough to change tremendously the momentum of the electron; the mere observation of the electron affects its motion so much that it can knock it entirely out of its orbit.
It is therefore impossible to determine the position and the momentum simultaneously to arbitrary accuracy. If a particle were localized, its wave function would become zero everywhere else and its wave would then have a very short wavelength. According to de Broglie’s relation p = ℏ /λ,
Time Energy Uncertainty Relation
The momentum of this particle will be rather high. Formally, this means that if a particle is accurately localized (i.e., ∆x 
0), there will be total uncertainty about its momentum (i.e., ∆px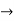 
∞).
Since all quantum phenomena are described by waves, we have no choice but to accept limits on our ability to measure simultaneously any two complementary variables.
Heisenberg’s uncertainty principle can be generalized to any pair of complementary, or canonically conjugate, dynamical variables: it is impossible to devise an experiment that can measure simultaneously two complementary variables to arbitrary accuracy .If this were ever achieved, the theory of quantum mechanics would collapse.
Energy and time, for instance, form a pair of complementary variables. Their simultaneous measurement must obey the time–energy uncertainty relation:
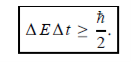
This relation states that if we make two measurements of the energy of a system and if these measurements are separated by a time interval ∆t, the measured energies will differ by an amount ∆E which can in no way be smaller than ℏ /∆t. If the time interval between the two measurements is large, the energy difference will be small. This can be attributed to the fact that, when the first measurement is carried out, the system becomes perturbed and it takes it a long time to return to its initial, unperturbed state. This expression is particularly useful in the study of decay processes, for it specifies the relationship between the mean lifetime and the energy width of the excited states.
In contrast to classical physics, quantum mechanics is a completely indeterministic theory. Asking about the position or momentum of an electron, one cannot get a definite answer; only a probabilistic answer is possible.
According to the uncertainty principle, if the position of a quantum system is well defined its momentum will be totally undefined.
1 Example: The uncertainty in the momentum of a ball travelling at 20m/s is 1×10−6 of its momentum. Calculate the uncertainty in position? Mass of the ball is given as 0.5kg.
Solution:
Given
v = 20m/s,
m = 0.5kg,
h = 6.626 × 10-34 m2 kg / s
Δp =p×1×10−6
As we know that,
P = m×v = 0.5×20 = 10kgm/s
Δp = 10×1×10−6
Δp = 10-5
Heisenberg Uncertainty principle formula is given as,
∆x∆p 
∆x 
∆x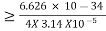 
∆x =0.527 x 10-29 m
2 Example: The mass of a ball is 0.15 kg & its uncertainty in position to 10–10m. What is the value of uncertainty in its velocity?
Solution:
Given
m=0.15 kg.
h=6.6×10-34 Joule-Sec.
Δx = 10 –10 m
Δv=?
Δx.Δv ≥h/4πm
Δv≥h/4πmΔx
≥6.6×10-34/4×3.14×0.15×10–10
≥ 3.50×10–24m
NANOTECHNOLOGY
Origin of Nano technology
While the word Nano technology is relatively new, the existence of nanostructures and Nano devices is not new. Such structures existed on the earth as life itself began though it is not known when humans to use nanosized materials the first known, Roman glassmakers were fabricated glasses containing nanosized metals. When the material size of the object is reduced to nanoscale, then it exhibits different properties than the same material in bulk form.
The concept and idea of nanotechnology original discussed first time in 1959 by Richard Feynman, the renowned physicist. Richard Feynman in his talk “There's Plenty of Room at the Bottom,” described the feasibility of synthesis via direct manipulation of atoms. However, in 1974, the term "Nano-technology" was first used by Norio Taniguchi.
Nanoscience
Nano science deals with the study of properties of materials at nano scales where properties differ significantly than those at larger scale.
Nanotechnology
Nanotechnology deals with the design, characterization, production and applications of nanostructures and nanodevices and nanosystems.
CHARATERIZATION
Physical properties
Inter atomic distance: When the material size is reduced to Nano scale, surface area to volume ratio increases. Due to increase of surface of surface area, more number of atoms will appear at the surface of compared to those inside. So Interatomic spacing decreases with size.
Thermal properties: Nano materials are different from that of bulk materials. The Debye Temperature and ferroelectric phase transition temperature are lower for nano materials. The melting point of nano gold decreases from 1200 K to 800K as the size of particle decreases form 300 Å to 200 Å.
Optical properties: Different sized nano particles scatters different of light incident on it and hence they appear with different colours. For example nano gold does not act as bulk gold. The nano particles of gold appear as orange, purple, red or greenish in colour depending on their grain size. The bulk copper is opaque whereas nanoparticle copper is transparent.
Magnetic properties: The magnetic properties of nano materials are different from that of bulk materials. In explaining the magnetic behaviour of nanomaterials, we use single domains unlike large number of domains in bulk materials. The coercivity value of single domain is very large.
For example, Fe, Co, and Ni are ferromagnetic in bulk but they exhibit super par magnetism. Na, K, and Rh are paramagnetic in bulk but they exhibit ferro-magnetic. Cr is anti-ferromagnetic in bulk but they exhibit super paramagnetic.
Mechanical properties: The mechanical properties such as hardness, toughness, elastic modulus, young’s modulus etc., of nano materials are different from that of bulk materials. In metals and alloys, the hardness and toughness are increased by reducing the size of the nano particles. In ceramics, ductility and super plasticity are increased on reducing grain size. Hardness increases 4 to 6 times as one goes from bulk Cu to nanocrystalline and it is 7 to 8 times for Ni.
Chemical properties
Nanocrystalline materials are strong, hard, erosion and corrosion resistant. They are chemically active and have the following chemical properties.
- In electrochemical reactions, the rate of increase in mass transport increases as the particle size decreases.
- The equilibrium vapour pressure, chemical potentials and solubilites of nanoparticles are greater than that for the same bulk material.
- Most of the metals do not absorb hydrogen. But the hydrogen absorption increases with the decrease of cluster size in Ni, Pt and Pd metals.
Basic principles of nanomaterials
When the material size of the object is reduced to nanoscale, then it exhibits different properties than the same material in bulk form. The factors that differentiates the nanomaterials from bulk material is
- Increase in surface area to volume ratio
- Quantum confinement effect
Increase in surface area to volume ratio: The ratio of surface area to volume ratio is large for nano materials.
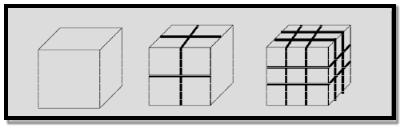
Example 1: To understand this let us consider a spherical material of radius ‘r’. Then its surface area to volume ratio is 3/r. Due to decrease of r, the ratio increases predominantly.
Example 2: For one cubic volume, the surface ratio is 6m2. When it is divided into eight cubes its surface area becomes 12m2. When it is divided into 27 cubes its surface area becomes 18m2. Thus, when the given volume is divided into smaller pieces the surface area increases.
6 Figure: |
Due to increase of surface of surface area, more number of atoms will appear at the surface of compared to those inside. For example, a nano material of size 10nm has 20% of its atoms on its surface and 3nm has 50% of its atoms. This makes the nanomaterials more chemically reactive and affects the properties of nano materials.
Quantum confinement effect: According to band theory, the solid atoms have energy bands and isolated atoms possess discrete energy levels. Nano materials are the intermediate state to solids and atoms. When the material size is reduced to nanoscale, the energy levels of electrons change. This effect is called quantum confinement effect. This affects the optical, electrical and magnetic properties of nanomaterials.
Nano materials
All materials are composed of grains. The visibility of grains depends on their size. Convectional materials have grains varying in size from hundreds of microns to millimetres. The materials processing grains size ranging from 1 to 100 nm, known as Nano materials. Nano materials can be produced in different dimensionalities.
- One dimensional nano material: Surface coatings and thin films
- Two dimensional nano materials: nano tubes nano wires, biopolymers
- Three dimensional nano materials: nano particles, precipitates, colloids, quantum dots, nano crystalline materials, fullerenes or carbon nano-60.
SYNTHESIS
Bottom-up and top-down approach to synthesis of nanomaterials
The synthesis of nanomaterials is key to the future success of this new technology. The methods of producing nanoparticles are classified into two main categories: Bottom-up approach
Top-down approach
BOTTOM UP APPROACH
In bottom-up approaches nanomaterials are assembled from basic building blocks, such as molecules or nanoclusters. The basic building blocks, in general, are nanoscale objects with suitable properties that can be grown from elemental precursors. The concept of the bottom-up approach is that the complexity of nanoscale components should reside in their self-assembled internal structure, requiring as little intervention as possible in their fabrication from the macroscopic world.
The bottom-up approach uses atomic or molecular feed-stocks as the source of the material to be chemically transformed into larger nanoparticles. This has the advantage of being potentially much more convenient than the top down approach. By controlling the chemical reactions and the environment of the growing nanoparticle, then the size, shape and composition of the nanoparticles may all be affected. For this reason nanoparticles produced by bottom up, chemically based and designed, reactions are normally seen as being of higher quality and having greater potential applications. This has led to the growth of a host of common bottom up strategies for the synthesis of nanoparticles. Many of these techniques can be tailored to be performed in gas, liquid, solid states, hence the applicability of bottom-up strategies to a wide range of end products. Most of the bottom up strategies requires suitable organometallic complexes or metal salts to be used as chemical precursors, which are decomposed in a controlled manner resulting in particle nucleation and growth. One of the key differences that can be used to subdivide these strategies into different categories is the method by which the precursor is decomposed.
A typical example of bottom-up is processing for nanocomposite magnets from individual high-magnetization and high-coercivity nanoparticles. The assembling critically depends on availability of anisotropic (single crystal) hard magnetic nanoparticles. Anisotropic nanoparticles produced via surfactant-assisted high energy ball milling satisfy the major requirements for this application.
7 Figure: |
TOP DOWN APPROACH
In top-down approaches, a bulk material is restructured (i.e. partially dismantled, machined, processed or deposited) to form nanomaterials. The aggressive scaling of electronic integrated circuits in recent years can be considered the greatest success of this paradigm. For top-down methods, the challenges increase as devices size is reduced and as the desired component designs become larger and more complex. Also the top-down assembly of nanocomponents over large areas is difficult and expensive.
The top-down method involves the systematic breakdown of a bulk material into smaller units using some form of grinding mechanism. This is beneficial and simple to execute and avoids the use of volatile and poisonous compounds frequently found in the bottom-up techniques. However, the quality of the nanoparticles formed by grinding is accepted to be poor in comparison with the material produced by modern bottom up methods. The main drawbacks include defect problems from grinding equipment, low particle surface areas, asymmetrical shape and size distributions and high energy needed to produce relatively small particles. Apart from these disadvantages, it must be distinguished that the nano-material produced from grinding still finds use, due to the simplicity of its manufacture, in applications including magnetic, catalytic and structural properties.
APPLICATIONS OF NANO SCIENCE AND NANOTECHNOLOGY
- Scanning electron microscopy has been applied to the surface studies of metals, ceramics, polymers, composites and biological materials for both topography as well as compositional analysis.
- An extension of this technique is Electron Probe Micro Analysis (EPMA), where the emission of X-rays, from the sample surface, is studied upon exposure to a beam of high energy electrons.
- Depending on the type of detectors used this method is classified in to two as: Energy Dispersive Spectrometry (EDS) and Wavelength Dispersive Spectrometry (WDS). This technique is used extensively in the analysis of metallic and ceramic inclusions, inclusions in polymeric materials and diffusion profiles in electronic components.
Nano materials possess unique and beneficial, physical, chemical and mechanical properties; they can be used for a wide verity of applications.
Material technology
- Nanocrystalline aerogel are light weight and porous, so they are used for insulation in offices homes, etc.
- Cutting tools made of Nano crystalline materials are much harder, much more wear- resistance, and last stranger.
- Nano crystalline material sensors are used for smoke detectors, ice detectors on air craft wings, etc.
- Nano crystalline materials are used for high energy density storage batteries.
- Nano sized titanium dioxide and zinc dioxide is used in sunscreens to absorb and reflect ultraviolet rays.
- Nano coating of highly activated titanium dioxide acts as water repellent and antibacterial.
- The hardness of metals can be predominately enhanced by using nanoparticles.
- Nanoparticles in paints change colour in response to change in temperature or chemical environment, and reduce the infrared absorption and heat loss.
- Nano crystalline ceramics are used in automotive industry as high strength springs, ball bearings and valve lifters.
Information technology
- Nanoscale fabricated magnetic materials are used in data storage
- Nanocomputer chips reduce the size of the computer.
- Nano crystalline starting light emitting phosphors are used for flat panel displays.
- Nanoparticles are used for information storage.
- Nanophotonic crystals are used in chemical optical computers.
Biomedical
- Biosensitive nanomaterials are used for ragging of DNA and DNA chips.
- In the medical field, nanomaterials are used for disease diagnosis, drug delivery and molecular imaging.
- Nano crystalline silicon carbide is used for artificial heart valves due to its low weight and high strength.
Energy storage
- Nanoparticles are used hydrogen storage.
- Nano particles are used in magnetic refrigeration.
- Metal nanoparticles are useful in fabrication of ionic batteries.
- Nano materials possess unique and beneficial, physical, chemical and mechanical properties; they can be used for a wide verity of applications.
Material technology
- Nanocrystalline aerogel are light weight and porous, so they are used for insulation in offices homes, etc.
- Cutting tools made of Nano crystalline materials are much harder, much more wear- resistance, and last stranger.
- Nano crystalline material sensors are used for smoke detectors, ice detectors on air craft wings, etc.
- Nano crystalline materials are used for high energy density storage batteries.
- Nano sized titanium dioxide and zinc dioxide is used in sunscreens to absorb and reflect ultraviolet rays.
- Nano coating of highly activated titanium dioxide acts as water repellent and antibacterial.
- The hardness of metals can be predominately enhanced by using nanoparticles.
- Nanoparticles in paints change colour in response to change in temperature or chemical environment, and reduce the infrared absorption and heat loss.
- Nano crystalline ceramics are used in automotive industry as high strength springs, ball bearings and valve lifters.
Information technology
- Nanoscale fabricated magnetic materials are used in data storage
- Nanocomputer chips reduce the size of the computer.
- Nano crystalline starting light emitting phosphors are used for flat panel displays.
- Nanoparticles are used for information storage.
- Nanophotonic crystals are used in chemical optical computers.
Biomedical
- Biosensitive nanomaterials are used for ragging of DNA and DNA chips.
- In the medical field, nanomaterials are used for disease diagnosis, drug delivery and molecular imaging.
- Nano crystalline silicon carbide is used for artificial heart valves due to its low weight and high strength.
Energy storage
- Nanoparticles are used hydrogen storage.
- Nano particles are used in magnetic refrigeration.
- Metal nanoparticles are useful in fabrication of ionic batteries.
