Unit 4
Intermolecular forces and potential energy surfaces
Ionic Interactions: This is also called as the charge- charge interaction and Electrostatic interaction. It is the specific type of chemical bond formed between the metal and a non-metal. The metals that are used is Alkali metals and Alkaline earth metal of periodic table. The used non-metal are halogens. E.g. NaCl. The interaction between the different metal took place just to complete the octet and attain a stability. The term octet means that the element has an eight electron in it’s outermost shell. There is a level of covalent-bond character in each ionic bond. However the purest ionic bond never exists as because of there is a level of covalent bond character in each ionic bond. As the general rule of thumb the larger the electro-negativity differences between the metal and non-metal the more ionic the bond and therefore the less covalent the bond will be.
The interactions between ions (ion - ion interactions) are the easiest to understand: like charges repel each other and opposite charges attract. These Columbic forces operate over relatively long distances in the gas phase. The force depends on the product of the charges (Z1, Z2) divided by the square of the distance of separation (d2):
F = - Z1Z2/d2
Two oppositely-charged particles flying about in a vacuum will be attracted toward each other, and the force becomes stronger and stronger as they approach until eventually they will stick together and a considerable amount of energy will be required to separate them. They form an ion-pair, a new particle which has a positively-charged area and a negatively-charged area. There are fairly strong interactions between these ion pairs and free ions, so that these the clusters tend to grow, and they will eventually fall out of the gas phase as a liquid or solid (depending on the temperature). They are very strong bonded with each other and having bond energy greater than 200 KJ/mole.
Induced Dipole:
An induced dipole moment is a temporary condition during which a neutral non-polar atom like Helium, undergoes a separation of charge due to the environment.
When an instantaneous dipole atom approaches a neighboring atom, it can cause that atom to produce dipoles.
The neighboring atom is then considered to have an induced dipole moment.
Spontaneous Dipole-Induced Interaction:
This is also called as the London Forces. The temporary attractive force that results when the electrons in the adjacent atoms occupy positions that make the atom form temporary dipoles. They are large networks of intermolecular forced between non-polar and non-charged molecules and atoms. The molecules that have induced dipole may also induce neighboring molecules to have dipole moment, so a large network of induced dipole interaction exists.
Dipolar Interactions:
Dipole-Dipole interactions result when two dipolar molecules interact with each other through space. When this occurs, the partially negative portion of one of the polar molecules is attracted to the partially positive portion of the second polar molecule. This type of interaction between molecules accounts for many physically and biologically significant phenomena such as the elevated boiling point of water.
Potential Energy of Dipole Interaction:
Potential energy is the maximum energy that is available for an object to do work. In physics, work is a quantity that describes the energy expended as a force operates over a distance. Potential energy is positional because it depends on the forces acting on an object at its position in space. For instance, we could say that an object held above the ground has a potential energy equal to its mass x acceleration due to gravity x its height above the ground. This potential energy that an object has as a result of its position can be used to do work. For instance we could use a pulley system with a large weight held above the ground to hoist a smaller weight into the air. As we drop the large weight it converts its potential energy to kinetic energy and does work on the rope which lifts the smaller weight into the air. It is important to remember that due to the second law of thermodynamics, the amount of work done by an object can never exceed (and is often considerably less) than the objects potential energy.
On a subatomic level, charged atoms have an electric potential which allows them to interact with each other. Electric potential refers to the energy held by a charged particle as a result of it's position relative to a second charged particle. Electric potential depends on charge polarity, charge strength and distance. Molecules with the same charge will repel each other as they come closer together while molecules with opposite charges will attract. For two positively charged particles interacting at a distance r, the potential energy possessed by the system can be defined using Coulomb's Law:
V=kQq/r
where
k is the Coulomb constant and
Q and q refer to the magnitude of the charge for each particle in Coulombs.
The above equation can also be used to calculate the distance between two charged particles (r) if we know the potential energy of the system. While Coulomb's law is important, it only gives the potential energy between two point particles. Since molecules are much larger than point particles and have charge concentrated over a larger area, we have to come up with a new equation.
The potential energy possessed by two polar atoms interacting with each other depends on the dipole moment, μ, of each molecule, the distance apart, r, and the orientation in which the two molecules interact. For the case in which the partially positive area of one molecule interacts only with the partially negative area of the other molecule, the potential energy is given by:
V(r)=−2μ1μ2/4πϵor3 |
Where, ϵo is the permeability of space. If it is not the case that the molecular dipoles interact in this straight end to end manor, we have to account mathematically for the change in potential energy due to the angle between the dipoles. We can add an angular term to the above equation to account for this new parameter of the system:
V(r)=−μ1μ2 /4πϵ0r312(cosθ12−3cosθ1cosθ2) |
In this formula θ12θ12 is the angle made by the two oppositely charged dipoles, and r12r12 is the distance between the two molecules. Also, θ1θ1 and θ2θ2 are the angles formed by the two dipoles with respect to the line connecting their centers.
It is also important to find the potential energy of the dipole moment for more than two interacting molecules. An important concept to keep in mind when dealing with multiple charged molecules interacting is that like charges repels and opposite charges attract. So for a system in which three charged molecules (2 positively charged molecules and 1 negatively charged molecule) are interacting, we need to consider the angle between the attractive and repellant forces.
Van Der Waal’s Interaction:
The intermolecular force of attraction between molecules is called Vander Waal’s forces. This force can be exhibit between any 2 non-polar molecules or 2 polar polar or non-polar molecules even though it can exert between ion polar and ion ion non-polar molecule.
Types of Vander Waal’s Forces:
(i) Ion-dipole interaction: The force that exerts between the cation or anion with presence of another polar molecule. E.g. It can be seen in HCl. The Hydrogen and Cl of same molecule are bonded with ionic bond while it is further attached to other component of same element with Vander Waal Forces.
(ii) Dipole-Dipole Interaction: This is the interaction between 2 different polar molecules. This is one of the second strongest Vander Waal Forces.
(iii) Ion-Induced Dipole Interaction: In the type of Vander Waal interaction one molecule is ionic while other one is non-polar molecule. The non-polar molecule induced by the effect of first element.
(iv) Dipole-Induced Dipole Interaction: In this type of Vander Waal interaction there are one polar and other one non-polar molecule. So the polar molecule makes the non-polar molecule to be polarized.
(v) Instantaneous Dipole-Induced Dipole Interaction: In this the both molecule are non-polar. The first molecule is become polarized instantly on the condition when the electron of a molecule revolving around the nucleus and at the instant time at which all the electron are oriented at a single place and hence that tend to result in the formation of another non-polar molecule to be polarized. This is also called as the London Forces or Dispersion Forces.
Vander Waals forces include attraction and repulsions between atoms, molecules, and surfaces, as well as other intermolecular forces. They differ from covalent and ionic bonding in that they are caused by correlations in the fluctuating polarizations of nearby particles. Intermolecular forces have four major contributions:
A repulsive component resulting from the Pauli Exclusion Principle that prevents the collapse of molecules.
Attractive or repulsive electrostatic interactions between permanent charges (in the case of molecular ions), dipoles (in the case of molecules without inversion centre), quadrupoles (all molecules with symmetry lower than cubic), and in general between permanent multipoles. The electrostatic interaction is sometimes called the Keesom interaction or Keesom force after Willem Hendrik Keesom.
Induction (also known as polarization), which is the attractive interaction between a permanent multipole on one molecule with an induced multipole on another. This interaction is sometimes called Debye force after Peter J.W. Debye.
Dispersion (usually named London dispersion interactions after Fritz London), which is the attractive interaction between any pair of molecules, including non-polar atoms, arising from the interactions of instantaneous multipoles.
The main characteristics of van der Waals forces are:
- They are weaker than normal covalent and ionic bonds.
- Van der Waals forces are additive and cannot be saturated.
- They have no directional characteristic.
- They are all short-range forces and hence only interactions between the nearest particles need to be considered (instead of all the particles). Van der Waals attraction is greater if the molecules are closer.
- Vander Waals forces are independent of temperature except for dipole – dipole interactions.
Derivation of Vander Waals equation: For a real gas, using Vander Waals equation, the volume of a real gas is given as (Vm – b), where b is the volume occupied by per mole. Therefore, ideal gas law when substituted with V = Vm – b is given as: P(Vm−b)=nRT Because of intermolecular attraction P was modified as below (P+aV2m)(Vm−b)=RT (P+an2V2)(V−nb)=nRT Where, Vm: molar volume of the gas R: universal gas constant T: temperature P: pressure V: volume Thus, Vander Waals equation can be reduced to ideal gas law as PVm = RT. Vander Waals Equation Derivation for one mole of gas: Following is the derivation of Vander Waals equation for one mole of gas that is composed of non-interacting point particles which satisfies ideal gas law: p=RTVm =RTv p =RTVm−b C =NaVm (proportionality between particle surface and number density) a′C2=a′(NA/VM)2 =a/V2m p =RT/(Vm−b)−(a/V2m) ⇒(p+aV2m)(Vm−b) =RT (p+n2a/V2)(V−nb) =nRT (substituting nVm = V) Van der Waals equation applied to compressible fluids: Compressible fluids like polymers have varying specific volume which can be written as follows: (p+A)(V−B)=CT Where, p- pressure V- specific volume T- temperature |
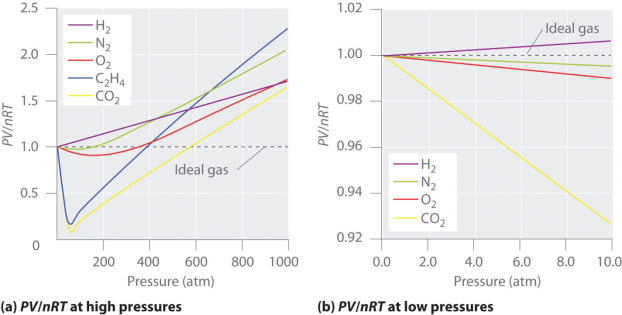
The gases which does not behave like ideal gases are called as the real gases. Their behavior can be explained by the interactions between the gaseous molecules. These intermolecular interactions between the gas particles are the reason why real gases do not adhere to the ideal gas law. Therefore, real gases can be defined as non ideal gases whose molecules occupy a given amount of space and have the ability to interact with each other.
It is important to note that in most cases, the behavior of a real gas is almost the same as that of an ideal gas. Therefore, in many applications, a detailed analysis of the deviation of real gases from ideal behavior is unnecessary. Reasonably accurate calculations can be conducted by applying the ideal gas equation to these real gases. However, it is important to note that a gas must be considered as a real gas when it is approaching its condensation point. Furthermore, almost all gases must be considered as real gases as they approach their critical points. Other situations in which gases can be considered as real gases include situations in which the pressure applied to the gas is very high, and in order to explain the Joule-Thomson effect. It is also important to note that the deviation of a real gas from the behavior of an ideal gas can be expressed in terms of the compressibility factor (also known as the gas deviation factor or the compression factor; usually denoted by the symbol ‘Z’).
The ideal gas laws is helpful in describing the behavior of a huge number chemically diverse substances as they exist in the gaseous state under ordinary environmental conditions, roughly around 1 atm pressure with a temperature of 300 K. But the condition on which temperature is reduced or the pressure is raised, the relation PV = constant that defines the ideal gas begins to break down, and its properties become unpredictable; eventually the gas condenses into a liquid.
- the average distance between collisions
- at sufficiently high pressures and low temperatures, intermolecular attractions assume control and the gas condenses to a liquid;
- the viscosity of a gas flowing through a pipe
|
Even so, many of the common laws such as Boyle's and Charles' continue to describe these gases quite well even under conditions where these phenomena are evident. Under ordinary environmental conditions (moderate pressures and above 0°C), the isotherms of substances we normally think of as gases don't appear to differ very greatly from the hyperbolic form
PV = constant
RT
Critical Phenomena:
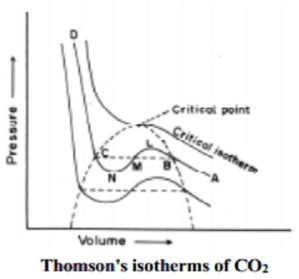
The essential condition for the liquefaction of the gas is described by the study of critical temperature, critical pressure and critical volume and their inter relationships.
|
When a gaseous system is transformed to its liquid state, there is a tremendous decrease in the volume. This decrease in volume can be effectively brought about by lowering of temperature or by increasing pressure. In both these effects the gaseous molecules come closer to each other and experience an increase in force of attraction which results in liquefaction of gases. At any constant temperature when pressure is increased volume is decreased and vice versa. Such P-V curves at constant temperature are known as isotherms.
|
The figure shows the continuous decrease in pressure with increase in volume for both ideal and real gases. There is a definite deviation exhibited by the real gas from ideal gas behavior at high pressure and low volumes.
Critical temperature (Tc)
It is defined as the characteristic temperature of a gas at which increase in pressure brings in liquefaction of gas above which no liquefaction occurs although the pressure may be increased many fold. For instance Tc of CO2 is 31.1 o C. This means that it is not possible to liquefy CO2 by applying pressure when its temperature is above 31.1 o C.
Critical pressure (Pc)
It is defined as the minimum pressure required to liquefy 1 mole of a gas present at its critical temperature.
Critical volume (Vc)
The volume occupied by 1 mole of a gas at its critical pressure and at critical temperature is the critical volume (Vc) of the gas.
A gas is said to be at its critical state when its pressure, volume and temperature are Pc, Vc and Tc.
Classical thermodynamics has a formal structure which serves to organise knowledge and to establish relationships between well–defined quantities. It is in this context that extensive observations are taken to imply that energy is conserved. Therefore, the change in the internal energy ∆U of a closed system is given by
∆U = q − w ………………………(1)
|
where q is the heat transferred into the system and w is the work done by the system. The historical sign convention is that heat added and work done by the system is positive, whereas heat given off and work done on the system are negative. Equation 1 may be written in differential form as
dU = dq – dw …………………….(2) For the special case where the system does work against a constant atmospheric pressure, this becomes dU = dq − P dV ………………………(3) where P is the pressure and V the volume. The specific heat capacity of a material is an indication of its ability to absorb or emit heat during a unit change in temperature. It is defined formally as dq/dT; since dq = dU + P dV , the specific heat capacity measured at constant volume is given by: CV = µ ∂U ∂T ¶ V ………………(4) It is convenient to define a new function H, the enthalpy of the system: H = U + P V ………………….(5) A change in enthalpy takes account of the heat absorbed at constant pressure, and the work done by the P ∆V term. The specific heat capacity measured at constant pressure is therefore given by: CP = µ ∂H ∂T ¶ P
|
Entropy: Entropy is used to describe the behavior of a system in terms of thermodynamic properties such as temperature, pressure, entropy, and heat capacity. This thermodynamic description took into consideration the state of equilibrium of the systems.
Meanwhile, the statistical definition which was developed at a later stage focused on the thermodynamic properties which were defined in terms of the statistics of the molecular motions of a system. Entropy is a measure of the molecular disorder.
Free energy: In thermodynamics, energy-like property or state function of a system in thermodynamic equilibrium. Free energy has the dimensions of energy, and its value is determined by the state of the system and not by its history. Free energy is used to determine how systems change and how much work they can produce. It is expressed in two forms: the Helmholtz free energy F, sometimes called the work function, and the Gibbs free energy G. If U is the internal energy of a system, PV the pressure-volume product, and TS the temperature-entropy product (T being the temperature above absolute zero), then F = U − TS and G = U + PV − TS. The latter equation can also be written in the form G = H – TS, where H = U + PV is the enthalpy. Free energy is an extensive property, meaning that its magnitude depends on the amount of a substance in a given thermodynamic state.
Thermodynamic principles can be employed to derive a relation between electrical energy and the maximum amount of work (Wmx).
The maximum amount of work obtainable from the cell is the product of charge flowing per mole and maximum potential difference E, through which the charge is transferred.
Wmax=−nFE
where,
n= number of moles electrons transferred
F= Faraday (96495 coulombs)
E=emf of the cell
According to thermodynamics,
Wmax=ΔG
∴ΔG=−nFE
when E is positive, ΔG is positive, ΔG will be negative and the cell reaction is spontaneous.
The electrode potential is defined as the Potential difference developed between the metal ions from metal to the solution or from solution to the metal. At equilibrium the potential difference remains constant. The electrode potential of a metal is defined as the direct measure of its tendency to get reduced is called reduction potential, its value is +x volts. Similarly the tendency of an electrode to lose electrons is a measure of its tendency to get oxidized is called oxidation potential, its value is –x volts.
Expression of electrode potential: Consider the following redox reaction Mn+ + ne- ↔ M For such a redox reversible reaction, the free energy change (∆ G) and its equilibrium constant (K) are related as; ∆ G = -RT ln k + RT ln [product]/[Reactant] ∆ G0 + RT ln [product]/[Reactant]………………..(i) Where ∆ G 0 = standard free energy change. The above equation is known as Van’t Hoff Isotherm. The decrease in free energy in the reversible reaction will produce electrical energy i.e. -∆ G = nEF and ∆ G 0 = -nE0F…………………………(ii) Where E = Electrode potential E0 = Standard electrode potential F = Faraday (96,500 coulombs) Comparing equation 1 & 2 -nEF = -nE0F + RT ln [M]/[Mn+] = -nE0F + Rt ln 1/ [Mn+] Where, concentration of the metal is unity or -nEF = -nE0F - RT ln [Mn+] Dividing the equation by –nF E= E0 + RT ln [Mn+]/nF E= E0 + 2.303RT log [Mn+]/nF E= E0 + 0.0591 log [Mn+]/n ……………(iii) This equation-3 is known as “Nernst Equation” for electrode potential
|
This equation is named after the name of scientist who discovered is Walther Nernst. Nernst equation plays a major role in relating the Reduction Potential with the electrode potential, temperature of the chemicals which are undergoing the oxidation or reduction.(Reduction Potential is used to measure the tendency of the chemical species to acquire or loose electron to an electrode.)
Gibbs free energy: Gibbs free energy of the system is the difference of enthalpy of the system with the product of temperature times the entropy of the system. G=H-TS
While at constant temperature this reaction transform into:
The Nernst Equation is derived from the Gibbs free energy under standard conditions. E*=E*reduction-E*oxidation ………..(i)
Where, n=no. of transferred electrons in the reaction F= Faraday constant E=Potential Difference. While when we see in the standard condition then, equation (ii) becomes
Hence, Reaction is Spontaneous when E* is positive while non- spontaneous in vice-versa.
−nFE=−nFEo+RTlnQ …………….(v) On Dividing both sides of the Equation above by −nF, E=E*−RTnFlnQ(6) ……….(vi) Equation (vi) in the form of log10: E=E*−2.303RT/nF log10Q …….(vii) At standard temperature T = 298 K, the 2.303RT/F term equals 0.0592 V and Equation (vii) can be rewritten: E=E*−0.0592V/n log10Q ……..(viii)
Then on substituting the these values to Nernst Equation we get, 0=E*-RT/nF In K …….(ix) At room temperature it becomes; 0=E*-0.0592V/n Log10K LogK=nE*/0.0592V The above equation clearly indicates the equilibrium constant K is proportional to the standard potential.
|
Reference Books
1. B. H. Mahan University chemistry, Pearsons Publication, 4th edition
2. M. J. Sienko and R. A. Plane, Chemistry: Principles and Applications,
3. C. N. Banwell, Fundamentals of Molecular Spectroscopy,Mcgraw Higher Ed., 4th edition.
4.P. W. Atkins, Physical Chemistry, Oxford University Press, 7th edition.
5. J. D. Lee Concise Inorganic Chemistry ,Oxford University Press, 5 th edition
6. Puri,Sharma, Kalia, Principles of Inorganic Chemistry