Unit 5
Complex Number
In probability theory and statistics, complex random variables are a generalization of real-valued random variables to complex numbers, i.e. the possible values a complex random variable may take are complex numbers.[1] Complex random variables can always be considered as pairs of real random variables: their real and imaginary parts. Therefore, the distribution of one complex random variable may be interpreted as the joint distribution of two real random variables.
Some concepts of real random variables have a straightforward generalization to complex random variables—e.g., the definition of the mean of a complex random variable. Other concepts are unique to complex random variables.
* A complex random variable Z on the probability space (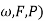 is a function on Z:
is a function on Z: 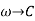 ,such that both its real part R(z) and its imaginary part i(z) are real random variables on .
,such that both its real part R(z) and its imaginary part i(z) are real random variables on . .
.
Circular symmetric complex normal random variables are used extensively in signal processing, and are sometimes referred to as just complex normal in signal processing literature. Formally, is a standard complex normal random variable.
The characteristic function of complex normal distribution is given by is a n -dimensional complex vector. Central limit theorem. If. The modulus of a complex normal random variable follows a Hoyt distribution
Example:1 Find fourth root of 
Solution: Convert 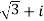 to polar first: r=
to polar first: r=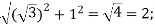
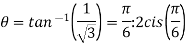
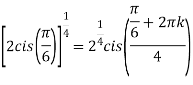

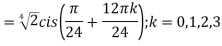
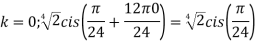
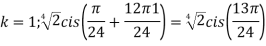
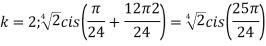
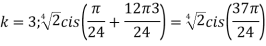
Example:2 Find the fifth root of 4-4i of 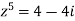
Solution: Convert 4-4i to polar: r=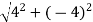 =
=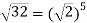 ;
;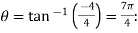 (
(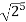 )cis(
)cis(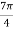 )
)
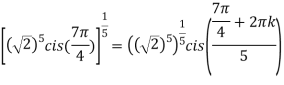

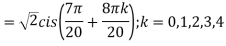
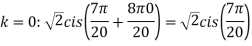
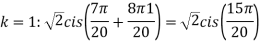
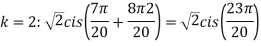
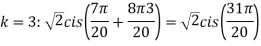
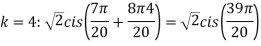
Example1: Solve cosh2 x – sinh2 x
Solution:
Given: cosh2 x – sinh2 x
We know that
Sinh x = [ex– e-x]/2
Cosh x = [ex + e-x]/2
Cosh2 x – sinh2 x = [ [ex + e-x]/2 ]2 – [ [ex – e-x]/2 ]2
Cosh2 x – sinh2 x = (4ex-x) /4
Cosh2 x – sinh2 x = (4e0) /4
Cosh2 x – sinh2 x = 4(1) /4 = 1
Therefore, cosh2 x – sinh2 x = 1
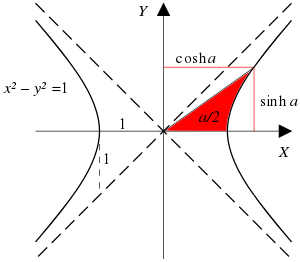
A ray through the unit hyperbola  in the point
in the point  , where
, where  is twice the area between the ray, the hyperbola, and the
is twice the area between the ray, the hyperbola, and the  -axis
-axis
Example 2:
Find the inverse of the function f(x) = ln(x – 2)
Solution:
First, replace f(x) with y
So, y = ln(x – 2)
Replace the equation in exponential way , x – 2 = ey
Now, solving for x,
x = 2 + ey
Now, replace x with y and thus, f-1(x) = y = 2 + ey
Example 3:
To solve an equation: f(x) = 2x + 3, at x = 4
Solution:
We have,
f(4) = 2 × 4 + 3
f(4) = 11
Now, let’s apply for reverse on 11.
f-1(11) = (11 – 3) / 2
f-1(11) = 4
Magically we get 4 again.
Therefore, f(f(4)) = f(4)
So, when we apply function f and its reverse f-1 gives the original value back again, i.e, f-1(f(x)) = x.
Example1: Prove that function 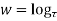 is analytic function.
is analytic function.
Solution. Real and Imaginary parts of 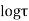 are
are
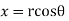
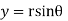
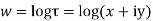
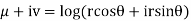
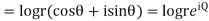
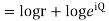
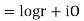
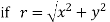
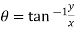
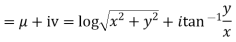
If, 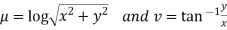
On differentiating u,v we get
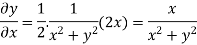

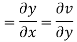
Again differentiating
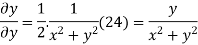
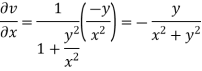
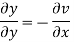
Example2: Determine P such that the function 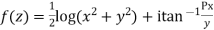 analytic
analytic
Solution: 
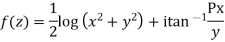
Hence 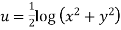
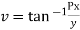
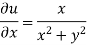
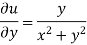
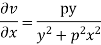
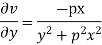
f(z) is analytic Cauchy Riemann should be satisfied that is
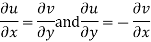
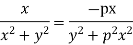
And 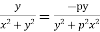
P=-1
Example 1:
Problem: simplify 16 i+10i (3-i)
Solution:
Given,
16i +10i (3-i)
=16i+10i (3i) +10 i(-i)
=16i+30i-10i2
=46i-10(-1)
=46i+10
Here real part is 10 and imaginary part is 46
Example 2:
Problem: express the following into a+ib form
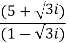
Solution:
Given., 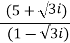
z = 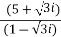
 =
= 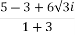 =
=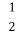 +
+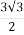 i
i
Modulus , 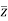 =
= 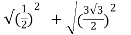 =
=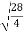 =
= 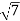
Conjugate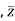 = (
= ( -
- 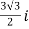
Reference Book:
1. G.B. Thomas and R.L. Finney, Calculus and Analytic geometry, 9th Edition, Pearson, Reprint, 2002.
2. Erwin kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley & Sons,2006.
3. Veerarajan T., Engineering Mathematics for the first year, Tata McGraw-Hill, New Delhi,2008.
4. Ramana B.V., Higher Engineering Mathematics, Tata McGraw Hill New Delhi, 11th Reprint, 2010.
5. D. Poole, Linear Algebra: A Modern Introduction, 2nd Edition, Brooks/Cole, 2005.
6. B.S. Grewal, Higher Engineering Mathematics, Khanna Publishers, 36th Edition, 2010