Unit 3
Partial Differentiation
Partial Differentiation
If 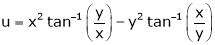
Prove that 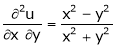
Partial differentiation of function of function
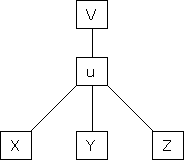
If z = f(u) and 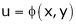 . Then z becomes a function of x & y. In this case, z becomes a function of x & y.
. Then z becomes a function of x & y. In this case, z becomes a function of x & y.
i.e.
Then
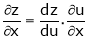 ,
,
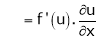
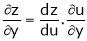
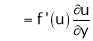
Similarly
If 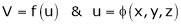
Then z becomes a function of x, y & z.
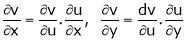
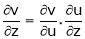 …………….
…………….
- If
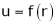 where
where 
Prove that
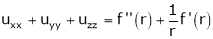
2. If V = 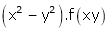 show that
show that
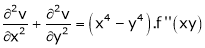
3. If 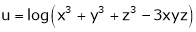 show that
show that
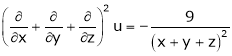
4. If 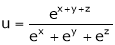 then prove that
then prove that
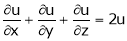
A polynomial in x & y is said to be Homogeneous expression in x & y of degree n. If the degree of each term in the expression is same & equal to n.
e.g.
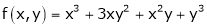 is a homogeneous function of degree 3.
is a homogeneous function of degree 3.
To find the degree of homogeneous expression f(x, y).
- Consider
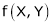
- Put
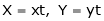 . Then if we get
. Then if we get 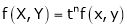 .
.
Then the degree of 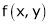 is n.
is n.
Ex.
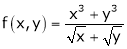
Consider 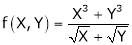
Put 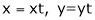
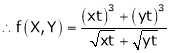
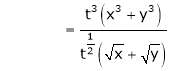
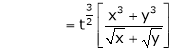
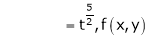 .
.
Thus degree of f(x, y) is 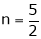
Note that
If 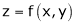 be a homogeneous function of degree n then z can be written as
be a homogeneous function of degree n then z can be written as

Differentiation of Implicit function
Suppose that we cannot find y explicitly as a function of x. But only implicitly through the relation f(x, y) = 0.
Then we find 
Since 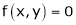
 diff. P. w.r.t. x we get
diff. P. w.r.t. x we get
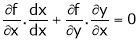
i.e. 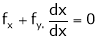
Similarly,
It f (x, y, z) = 0 then z is called implicit function of x, y. Then in this case we get
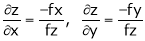
Ex.
Find 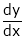 if
if 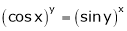
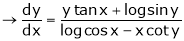
Ex. Find  . If
. If 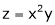 , &
, & 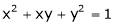
Ex. If 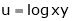 , where
, where 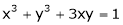
Find 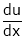
Ex. If 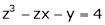
Then find 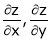
Eulers Theorem on Homogeneous functions:
Statement:
If 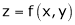 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,
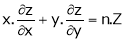
Deductions from Euler’s theorem
- If
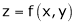 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,
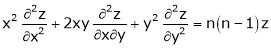 .
.
2. If 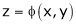 be a homogeneous functions of degree n in x & y and also
be a homogeneous functions of degree n in x & y and also 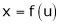 then,
then,
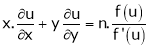
And
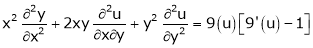
Where 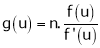
Ex.
If  , find the value of
, find the value of
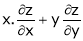
Ex.
If 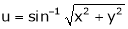 then find the value of
then find the value of 
Ex. If 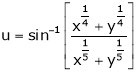 then prove
then prove
That 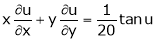
Ex. If  the prove that
the prove that
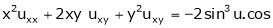
Ex. If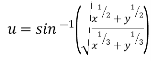 then show
then show
That 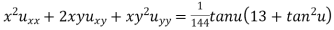
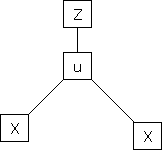
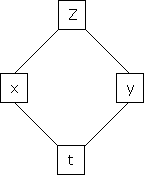
a) Let 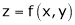 and
and 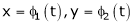 , then z becomes a function of
, then z becomes a function of 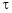 , In this case, z is called a composite function of
, In this case, z is called a composite function of 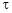 .
.
i.e.
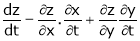
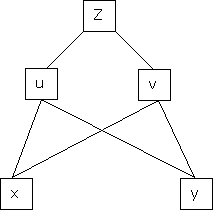
b) Let  possess continuous partial derivatives and let
possess continuous partial derivatives and let 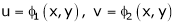 possess continuous partial derivatives, then z is called a composite function of x and y.
possess continuous partial derivatives, then z is called a composite function of x and y.
i.e.

&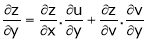
Continuing in this way, …..
Ex. If 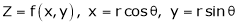 Then prove that
Then prove that
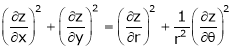
Ex. If 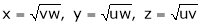 then prove that
then prove that
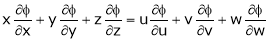
Where  is the function of x, y, z.
is the function of x, y, z.
Ex. If 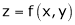 where
where 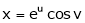 ,
,
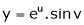 then show that,
then show that,
i) 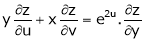
Ii) 
Notations of partial derivatives of the variable to be treated as a constant
Let
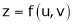 and
and 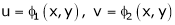
i.e.

Then  means the partial derivative of u w.r.t. x treating y const.
means the partial derivative of u w.r.t. x treating y const.
To find 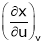 from given reactions we first express x in terms of u & v.
from given reactions we first express x in terms of u & v.
i.e. 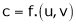 & then diff. x w.r.t. u treating v constant.
& then diff. x w.r.t. u treating v constant.
To find 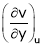 express v as a function of y and u i.e.
express v as a function of y and u i.e.  then diff. v w.r.t. y treating u as a const.
then diff. v w.r.t. y treating u as a const.
Ex. If  ,
, 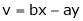 then find the value of
then find the value of
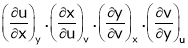 .
.
Ex. If  ,
, 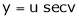 then prove that
then prove that
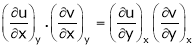
Let 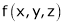 be a function of x, y, z which to be discussed for stationary value.
be a function of x, y, z which to be discussed for stationary value.
Let 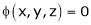 be a relation in x, y, z
be a relation in x, y, z
 for stationary values we have,
for stationary values we have,

i.e. 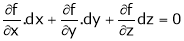 … (1)
… (1)
Also from 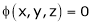 we have
we have
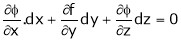 … (2)
… (2)
Let ‘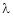 ’ be undetermined multiplier then multiplying equation (2) by
’ be undetermined multiplier then multiplying equation (2) by 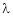 and adding in equation (1) we get,
and adding in equation (1) we get,
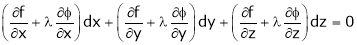
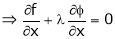 … (3)
… (3)
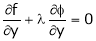 … (4)
… (4)
 … (5)
… (5)
Solving equation (3), (4) (5) & we get values of x, y, z and 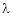 .
.
- Decampere a positive number ‘a’ in to three parts, so their product is maximum
Solution:
Let x, y, z be the three parts of ‘a’ then we get.
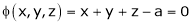 … (1)
… (1)
Here we have to maximize the product
i.e. 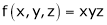
 By Lagrange’s undetermined multiplier, we get,
By Lagrange’s undetermined multiplier, we get,
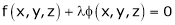
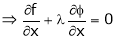 … (2)
… (2)
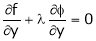 … (3)
… (3)
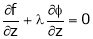 … (4)
… (4)
i.e.
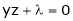 … (2)’
… (2)’
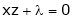 … (3)’
… (3)’
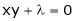 … (4)
… (4)
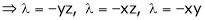
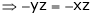
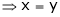
And 
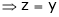
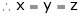
From (1)
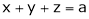
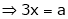
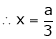
Thus 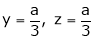 .
.
Hence their maximum product is 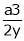 .
.
2. Find the point on plane  nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
Solution:
Let 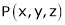 be the point on sphere
be the point on sphere 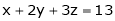 which is nearest to the point
which is nearest to the point 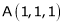 . Then shortest distance.
. Then shortest distance.
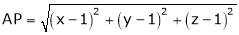
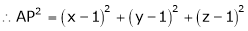
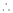 Let
Let 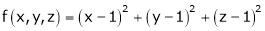
Under the condition 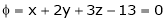 … (1)
… (1)
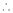 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have
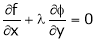
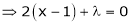 … (2)
… (2)
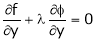
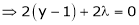 … (3)
… (3)
i.e. 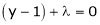 &
&

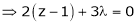 … (4)
… (4)
From (2) we get 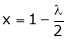
From (3) we get 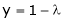
From (4) we get 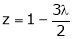
 Equation (1) becomes
Equation (1) becomes

i.e. 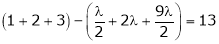
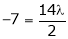

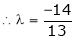
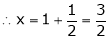
y = 2
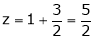
If 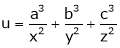 where x + y + z = 1.
where x + y + z = 1.
Prove that the stationary value of u is given by,
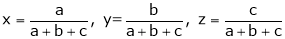
Reference Book:
1. G.B. Thomas and R.L. Finney, Calculus and Analytic geometry, 9th Edition, Pearson, Reprint, 2002.
2. Erwin kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley & Sons,2006.
3. Veerarajan T., Engineering Mathematics for the first year, Tata McGraw-Hill, New Delhi,2008.
4. Ramana B.V., Higher Engineering Mathematics, Tata McGraw Hill New Delhi, 11th Reprint, 2010.
5. D. Poole, Linear Algebra: A Modern Introduction, 2nd Edition, Brooks/Cole, 2005.
6. B.S. Grewal, Higher Engineering Mathematics, Khanna Publishers, 36th Edition, 2010