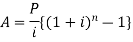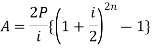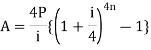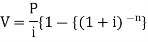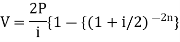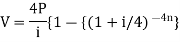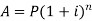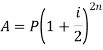UNIT – II
Commission
Introduction to commission and brokerage- problems on commission and brokerage
The amount received by the agency for providing its services is known as ‘brokerage’ or ‘commission’.
For example- placement agencies, marriage bureaus etc.
An individual can also run this type of business
Note- An individual who acts as a ‘middle man’ between a seller and buyer is known as broker.
Brokerage is paid by purchaser, Commission is paid by seller. Therefore
Net amount paid by purchaser = Sale price + brokerage
Net amount received by seller = Sale price - commission
Commission % = Commission
100 /Selling price
Selling Price = Commission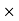
100/ Commission %
Commission (Brokerage) = Commission%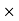
Selling price/100
Example: The Price of a book is Rs. 15.75. A book seller sells 1200 books and pays Rs 17,860.50 to the book publisher after deducting his commission.
Find the commission rate.
Sol.
Here we have total commission,
We have to find the total sale price of books.
The total sale price of books = Number of Books 
Price = 1200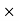
15.75 =18900
Commission = Sale price – Amount paid to the Publisher = 18900-17860.5 = 1039.5
Commission % = Commission
100 /Selling price = 1039.5
100/18900 = 5.5%
Example: Mahesh sold his car for Rs.68,000 with the help of an agent. If the commission paid by Mahesh is Rs 2550. Find rate of commission, and the net amount received by the Mahesh.
Sol.
Commission % = Commission
100 /Selling price = 2550
100/68000 = 3.75%
Net amount received by farmer = Sale price – Commission = 68000-2550 = Rs65, 450
Example: An agency pays 15% commission to a notebook distributor. The price of each notebook is Rs 3. If he sells 50 copies of notebook every day, find how much commission he receives in a month and also net amount received by the Agency?
Sol.
Price of each news paper = Rs 3.
Sale price for a day = Number copies sold in day 
price of Cost of news paper = 50
3 = Rs 150
Sale price for a year = Number of days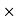
Sale price for a day = 30
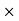150 = 450 Rs
Commission = Commission%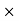
Selling price/100 = 15
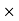450/100 = 67.5 Rs.
Net amount received by agency = selling price – commission = 450 -67.5 = 382.5 Rs
Key takeaways-
- Net amount paid by purchaser = Sale price + brokerage
Net amount received by seller = Sale price - commission
2. Commission % = Commission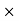
100 /Selling price
3. Selling Price = Commission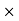
100/ Commission %
4. Commission (Brokerage) = Commission%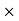
Selling price/100
Discount
Cost Price (CP) - The price at which an article is purchased.
Selling Price (SP) - This is the price at which an article is sold.
Profit - If the selling price is more than the cost price, then there will be profit
Profit = Selling price (SP) – Cost price (CP)
Profit % = (profit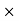
100)/CP
Loss - If the selling price is less than the cost price, then there will be loss
Loss = Cost price (CP) – Selling price (SP)
Loss% = (Loss 
100)/CP
Marked Price - This is the price marked as the selling price on an article, also known as the listed price
Note- Profit or Loss is always calculated on the cost price.
Discount: This is the reduction in price offered on the marked or listed price.
Example: Suppose the profit percentage is 80% of the cost. If the cost further increases by 20% but the selling price remains the same, how much is the decrease in profit percentage?
Sol.
Let us suppose
CP = Rs. 100.
Then Profit = Rs. 80 and selling price = Rs. 180.
The cost increases by 20% → New CP = Rs. 120, SP = Rs. 180.
Profit % = 60/120 
100 = 50%.
Therefore, Profit decreases by 30%.
Example: A dishonest shopkeeper sells his grocery using weights 15% less than the true weights and makes a profit of 20%. Find his total gain percentage.
Sol.
Suppose 1 kg of grocery bag.
Its actual weight is 85% of 1000 gm = 850 gm.
Let the cost price of each gram be Re. 1. Then the CP of each bag = Rs. 850.
SP of 1 kg of bag = 120% of the true CP
Therefore, SP = 120/100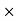 
1000 = Rs. 1200
Gain = 1200 – 850 = 350
Hence Gain % = 350/850 
100 = 41.17%
Example: A shopkeeper offers a discount of 20% on the selling price. On a special sale day, he offers an extra 25% off coupon after the first discount. If the article was sold for Rs. 3600, find the marked price of the article
Sol.
Let the marked price of the article be x.
First a 20% discount was offered, on which another 25% discount was offered.
So, 75% of 80% of x = 3600
75/100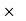 
80/100 
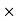x = 3600 → x = 6000.
So the article was marked at Rs. 6000.
Example: The cost price of 30 articles is equal to the selling price of 40 articles. What is the profit or loss percentage?
Sol.
CP of 30 articles = SP of 40 articles Or, CP/SP = 30/40 =3/4
Or, 1 – CP/SP = 1- 3/4 = 1/4
So, Loss percentage
= (l – CP/SP) x 100 = 1/4x 100 = 25%
Trade discount-
Trade discount is a certain percentage a manufacturer is willing to reduce its list price for wholesalers or retailers.
Trade discounts are given to wholesalers that order large quantities of a product as well as retailers with good relationships with the manufacturer. Purchase discounts or Cash discount are based on payment plans not order quantities.
Trade discounts are offered on bulk purchases by traders, wholesalers, distributors or retailers and not to the end consumers.
Trade discounts are generally offered at varied rates depending on the volume of sale
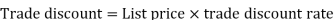
And
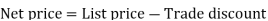
Example: Sweety purchases a set of toys that lists for Rs. 950 and it has a trade discount of 30%, then find the net price.
Sol.
As we know that-
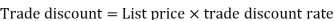
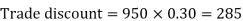
Then
Net price = 950 – 285 = 665
Example: If Raheem will buy a table that lists for Rs. 2000 and it has a trade discount of 50%. Then how much will he pay?
Sol.
As we know that-
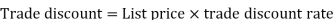
Then
Net price = 2000 – 1000 = 1000
Cash discount is allowed to stimulate instant payment of the goods purchased.
Cash Discount is referred to as a discount, allowed to customers by the seller at the time of making the payment of purchases, as a reduction in the invoice price of the commodity.
Both the buyers and sellers keep a proper record of such discount in their books of accounts.
Sellers offer cash discounts to their buyers as an incentive to encourage early payment.
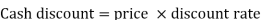
Ordinary dating method-
A credit term of [2/10, n/30] means that you will get a discount of 2% if you clear your account within 10 days
Example: A person received an invoice for Rs. 3,000 dated 22 November 2019 with terms [2/10, n/30]. He paid the whole amount on 30 November 2019. How much did he effectively paid for the bill?
Sol.
- Date of Invoice: 22nd November 2019
- Day 1 of the cash discount period. : 23rd November 2019
- Last day of the Cash discount period: 31st November 2019
- Date of payment: 30th November 2019
Cash discount.= Price 
Discount rate
= Rs. 3,000 
2/100
= Rs. 60
Amount effectively paid by the person = Bill value - Cash discount
= 3,000 - 60
= Rs. 2,940
Key takeaways-
- Cost Price (CP) - The price at which an article is purchased
- Selling Price (SP) - This is the price at which an article is sold
- Profit = Selling price (SP) – Cost price (CP)
- Profit = Selling price (SP) – Cost price (CP)
- Loss = Cost price (CP) – Selling price (SP)
- Loss% = (Loss
100)/CP - Marked Price - This is the price marked as the selling price on an article, also known as the listed price
- Discount: This is the reduction in price offered on the marked or listed price.
- Trade discount is a certain percentage a manufacturer is willing to reduce its list price for wholesalers or retailers.
- Trade discounts are generally offered at varied rates depending on the volume of sale
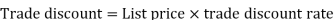
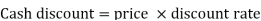
- Gaining Ratio = New Ratio – Old Ratio
A set of problems related to work and rate of work is presented with detailed solutions.
Problem 1: Solution to Problem 1: t × (1 / 1.5) t × (1 / 2) When the two work together, their work will be added. Hence t × (1 / 1.5) + t * (1 / 2) = 1 6 (t × (1 / 1.5) + t × (1 / 2) ) = 6 4 t + 3 t = 6 t = 6 / 7 hours = 51.5 minutes. Problem 2: Solution to Problem 2: 2 (1 / 6 + 1 / 8 + R) = 1
Problem 3: Solution to Problem 3:
Problem 4: Solution to Problem 4: t × (1 / 3) + (t - 1) × (1 / 6) = 1
|
The sales tax is a percent of the purchase price.
Sales Tax = Tax Rate • Purchase Price
Total Cost = Purchase Price + Sales Tax
Example 1: If a sweater has a total cost of $54 after tax, what is the cost of the sweater before tax, if the sales tax is 4.5%?
The total cost of the sweater is the original cost plus a 4.5% tax, which can be expressed in the equation:
TC=C+T
Where TC is the total cost, C is the original cost, and T is the tax. Now, we will plug in the information we know. Since the original cost of the sweater is unknown, we will use the variable x.
54=x+.045x
.045 is the decimal expression of 4.5%.
Now, solve for x. Consolidate the x variable.
54=1.045x
Divide both sides by 1.045.
51.67=x
$51.67 is the cost of the sweater before tax.
2. Kylie buys an article for $ 10000 and pays 7% tax. He sells the same article for $ 13000 and charges 9% tax. Find the VAT paid by Kylie.
Solution:
Cost of the article = 10000
Tax paid by Kylie = 7% of $ 10,000
= $ 7/100 × 10000
= $ 700
Selling price of the article = $ 13000
Tax charged at 9% = 9% of 13000
= $ 9/100 × 13000
= $ 1170
Therefore, VAT = tax recovered on sale - Tax paid on purchase.
= $ 1170 - $ 700
= $ 470
Therefore, VAT = $ 470
3. A retailer buys an article from the wholesaler at $80 and the wholesaler charges a sales tax at the prescribed rate of 8%. The retailer fixes the price at $ 100 and charges sales tax at the same rate. Apply value added tax system of sales tax calculation to answer the following questions.
(i) What is the price that a consumer has to pay to buy the article?
(ii) Find the input tax and output tax for the retailer.
(iii) How much VAT does the retailer pay to the government?
Solution:
(i) Here, the price P = $100, the rate of sales tax r% = 8%
Therefore, cost price for the consumer = P(1 + r/100)
= $100 × (1 + 8/100)
= $100 × 108/100
= $108
(ii) Input tax = tax paid by the retailer to the wholesaler
= 8% of $80
= 8/100 × $80
= $64/10
= $6.40
Output tax = tax realised by the retailer from the consumer
= 8% of $100
= 8/100 × $100
= $8
(iii) Value added tax paid by the retailer = output tax – input tax
= $8 - $6.40
= $1.60
4. A shopkeeper sells an article at its marked price $ 7500 and charges sales-tax at the rate of 12% from the customer. If the shopkeeper pays a VAT of $ 180, calculate the price inclusive of tax paid by the shopkeeper.
Solution:
Since, the shopkeeper sells the article for $ 7500 and charges sales-tax at the rate of 12%.
Therefore, the tax charged by the shopkeeper = 12% of $ 7500
= 1210012100 × 7500
= $ 900
Since, VAT = Tax charged – Tax paid
Or, $ 180 = $ 900 – Tax paid
Or, Tax paid by the shopkeeper = $ 900 - $ 180 = $ 720
If the shopkeeper buys the article for $ x
Tax on it = 12% of x = $ 720
Or, 1210012100 × x = $ 720
Or, x = $ 6000
Therefore, the price inclusive of tax paid by the shopkeeper = $ 6000 + $ 720 = $ 6720
5. A manufacturer printed the price of his goods as $120 per article. He allowed a discount of 30% to the wholesaler who in his turn allowed a discount of 20% on the printed price to the retailer. If the prescribed rate of sales tax on the goods is 10% and the retailer sells it to the consumer at the printed price then find the value added tax paid by the wholesaler and the retailer.
Solution:
For the manufacturer, the price of the article at which it is sold = Printed price – discount of the wholesaler
= $ 120 – 30% of $ 120
= $ 120 - $ 120 × 30/100
= $ 120 - $ 36
= $ 84
Therefore, input tax for the wholesaler = 10% of 84 = 10/100 × $ 84 = $ 8.40
For the wholesaler, the price of the article at which it is sold = Printed price – discount to the retailer
= $ 120 - 20% of 120
= $ 120 - $ 120 × 20/100
= $ 120 - $ 24
= $ 96
Therefore, output tax for the wholesaler = 10% of 96 = 10/100 × $ 96 = $ 9.60
Therefore, VAT payable for the wholesaler = output tax – input tax
= $ 9.60 - $ 8.40
= $ 1.20
For the retailer, the price of the article at which it is sold = printed price = $ 120
Therefore, output tax for the retailer = 10% of 120
= 10/100 × $ 120
= $ 12.
Input tax for the retailer = output tax for the wholesaler
= $ 9.60
Therefore, VAT payable by the retailer = output tax – input tax
= $ 12 - $ 9.60
= $ 2.40
Therefore, VAT paid by the wholesaler is $ 1.20 and that paid by retailer is $ 2.40
2.4 Stocks and Shares
Shares: The total capital in the company is divided into very small units. These units form the worth of a company. Each of this unit is called stock or a share.
Stock capital: To run a company, you require capital. And this total capital in a company is called as the stock capital.
Dividend: When the company makes a profit, it distributes it among its shareholders. This distribution of profit is known as the dividend. It is usually paid annually in the form of a percentage of a share.
Also, this dividend is only paid on the face value of any bond.
Shareholder: Perhaps the most important body in the organization are the shareholders. The shareholder of a company is the one who owns more than one share of the company.
As a part of authentication, the company issues a certificate to every shareholder describing the total number of shares given and it’s value.
Face value: The value that is printed on the certificate given to a stockholder or a shareholder it known as face value or a nominal value. Whatever happens, the face value of a share will always remain the same.
Brokerage: Different companies have different stocks and it can be traded by anyone in the market. This is done through brokers at the share market. The fee that these brokers charge is called the brokerage.
When a stock or a share is purchased, then the cost price is also added with a brokerage.
Also, when the stock is sold, this brokerage is deducted from the selling price.
Market value: Through brokers, you can trade and sell the stocks of the different companies in the market. This value of shares changes depending upon the market.
This change is called the market value of a stock or a share. There are conditions in a share:
- It is called at a below par or discount when the face value of a share is more than the market value
- The market value is at par when the face value is the same as the market value.
- It is above par or at a premium when the face value is less than the market value.
Examples of Stocks and Shares
1. Aakash wants to invest a part of Rs. 12000 at Rs. 120 in 12% stock. He wants to invest the remaining amount at Rs. 125 in 15% stock. The total dividend he receives per year is Rs. 1360. Find the amount that Aakash should invest in 12% stock at Rs. 120.
Suppose the investment that Aakash should do is Rs. X. So, the second investment by him will be 12000 – X.
Income on 1st share will be, 12/120 x X = X/10
Income for 2nd share, 15/125 x (12000 – X) = 3(12000 – X)/25
=> 3(12000 – X)/25 + X/10 = 1360
So, 72000 + 5X – 6X = 1360 x 50
=> X = 40000
So, the required answer is Rs. 40000.
2. What will be the market value Rs 3000 stock at Rs 95 at 614614 % per annum.
Solution: The market value of Rs 100 stock = Rs 95
∴∴ The market value 3000 stock = Rs 95100×300095100×3000 = Rs 2850
Question-2 A man sell his Rs 4000 stock at 5% at 5 premium. What sum will he get if the brokerage is 1818?
Solution: The s.p of Rs 100 stock Rs 100+rs 5 -Rs 1818
∴∴ s.p of Rs 4000 stock = 8398×40001008398×4000100 = Rs 4195
3. How much stock of 312312% can be bought fir rs 2140 at 1068910689 if the brokerage is 1919?
Solution: Sum paid Rs for 100 stock = Rs. 10689+rs1910689+rs19 = Rs 107
∴∴ The stock bought for Rs 107 = Rs 100
4. Michael buys shares of face value $ 50 of a company which pays 10 % dividend. At what price did he buy each share from the market if his profit is 16 % on his investment?
Solution:
Let the market value (M.V.) of each share be x.
The dividend is calculated on nominal value.
The dividend on one share = 10% of $ 50 = $ 5.
Therefore, he earned $ 5 on an investment of x.
A profit of 16 % on x = 1610016100 × x = 4x254x25
Therefore, 4x254x25 = $ 5
⟹ x = $25×5425×54
⟹ x = $12541254
⟹ x = $ 31.25
Therefore, Michael bought each share at $ 31.25 from the market.
5. Jackson buys $ 40 shares in a company, which pays 10% dividend. Jackson buys the share at such a price that his profit is 16% on his investment. At what price did Jackson buy the share?
Solution:
Dividend (profit) given by the company on 1 share = 10% of $ 40 = $ 4.
Suppose the man buys one share for x.
Therefore, Jackson’s profit = 16% of $ x = $ 16x10016x100
According to the problem, 16x10016x100 = 4
⟹ x = $ 25
Jackson bought the share at $ 25.
6. Robert bought shares of 6% $ 100 shares at $ 120. Adrian bought shares of 8% $ 20 shares at $ 30. Whose investment was better?
Solution:
6% $ 100 shares at $ 120
i.e., the annual income from 1 share of nominal value $ 100 is $ 6, investment for 1 share being $ 120.
Therefore, profit percentage = 61206120 × 100 % = 5%
Therefore, Robert’s shares give him a profit of 5%
8 % $ 20 shares at $ 30
i.e., the annual income from 1 share of nominal value $ 20 is $ 8×201008×20100 = $ 8585, investment for 1 share being $ 30.
Profit percentage = $85$30$85$30 × 100 %
= 163163 %
= 51313%
Therefore, Adrian’s shares give him a profit of 51313%
Therefore, Adrian’s investment was better.
2.5 Simple annuities
Annuity-
An annuity is a sequence of equal payment or a sequence of regular payment at regular intervals or in other words, An annuity is a fixed sum paid at regular intervals under certain conditions.
The length of time during which the annuity is paid can either be until the death of the recipient or for a guaranteed minimum term of years, irrespective of whether the annuitant is alive or not.
The time between payments is called the payment interval, and the time which the money is to be paid is called the term of the annuity.
Amount of an annuity:
Amount of an annuity is the total of all the installments left unpaid together with the compound interest of each payment for the period it remains unpaid.
The formulas to find the amount of annuity are given below-
| When annuity is payable annually and interest is also compounded annually |
| annuity is payable half-yearly and interest is also compounded half-yearly |
| annuity is payable quarterly and interest is also compounded quarterly |
Present value of an annuity-
Present value of an annuity is the sum of the present values of all payments (or installments) made at successive annuity periods
The formulas to calculate present value ‘V’ of an annuity P are given below-
| When V of an annuity P payable annually |
| When V of an annuity P payable half-yearly |
| When V of an annuity P payable quarterly |
The future value is calculated as-
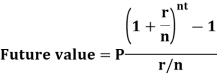
Example: Sundar decides to deposit 20,000rs. at the end of each year in a bank which pays 10% p.a. compound interest.
If the installments are allowed to accumulate, what will be the total accumulation at the end of 9 years?
Sol.
Suppose A rs. be the total accumulation at the end of 9 years. Then we get-
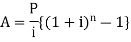
Here P = 20,000 rs., i = 10/100 = 0.1 and n = 9
Then
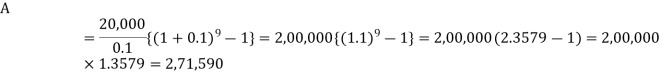
Hence the total required accumulation is 2,71,590 rs.
Example: Rajeev purchased a flat valued at 3,00,000rs. He paid 2,00,000 rs. at the time of purchase and agreed to pay the balance with interest of 12% per annum compounded half yearly in 20 equal half yearly installments.
If the first installment is paid after six months from the date of purchase, find the amount of each installment.
[Given log 10.6 = 1.0253 and log 31.19 = 1.494]
Sol.
Here 2,00,000 has been paid at the time of purchase when cost of the flat was 3,00,000, we have to
consider 20 equated half yearly annuity payment P when 12% is rate of annual interest compounded half
yearly for present value of 1,00,000rs.
So that-
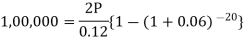
Or
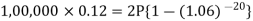
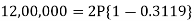
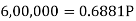
Then-
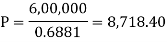
Hence the amount of each installment = 8,718.40
Suppose,
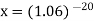
Taking log-
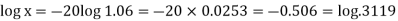
Hence
X = 0.3119
Key takeaways-
- Annuity-
An annuity is a fixed sum paid at regular intervals under certain conditions.
The length of time during which the annuity is paid can either be until the death of the recipient or for a guaranteed minimum term of years, irrespective of whether the annuitant is alive or not.
2. Amount of an annuity:
Amount of an annuity is the total of all the installments left unpaid together with the compound interest of each payment for the period it remains unpaid.
3. Present value of an annuity-
Present value of an annuity is the sum of the present values of all payments (or instalments) made at successive annuity periods
Stated annual rate and effective annual rate
Stated annual interest rate is the rate expressed as a per year percentage, by which interest payments are determined.
Or in other words, the stated annual interest rate is the return on an investment that is expressed as a per-year percentage.
It is also called quoted interest rate
It is the simple interest rate that the bank gives as the interest rate on loan.
Effective rate of interest-(EAR)
It is the equivalent annual rate of interest which is compounded annually.
Effective annual interest rate =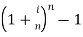 
Where i =actual rate of interest, n = compounding period.
Example: Rohan invests Rs. 5,000 in a term deposit plan. The plan offers an interest rate of 6% p.a., compounded quarterly. How much interest will John earn after one year? Also, what is the effective rate of interest?
Sol. Here we have-
P = 5000, i = 6% per annum or 0.06 p.a. or 0.015 per quarter
Compounding period = n = 4
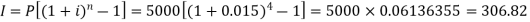
Rohan earns Rs. 306.82 interest after a year
Now the effective rate of interest is-
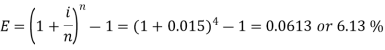
Example: What is the effective rate of interest on a CD that has a nominal rate of 9.5 percent with interest compounded monthly?
Sol.
Here we have,
i = 9.5% or 0.095
Now the effective rate of interest is-
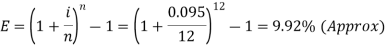
Example: Amitabh invested Rs. 100 in a scheme that pays out a nominal annual interest rate of 10% compounded on a quarterly basis. Find the Effective Annual Rate.
Sol.
Here we have,
i = 10% or 0.1
Now the effective rate of interest is-
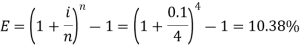
Key takeaways-
- the stated annual interest rate is the return on an investment that is expressed as a per-year percentage
- Effective annual interest rate =
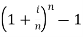
Where i =actual rate of interest, n = compounding period.
Calculation of interest is one of the most basic uses of mathematics in finance.
We can define the simple interest as- “the price has to be paid for the use of a certain amount of money or principal for certain period, is called interest”
Amount- This is the sum of the principal and the interest at any time.
The rate of interest is denoted by ‘i’.
Let the principal is 100 rs. And the interest is 8 then we can say that the rate of interest is 8 percent per annum or we can write it as r = 8%
Suppose ‘P’ is the principal and ‘n’ is the time for which the principal is given and ‘r’ be the rate of interest per annum
‘I’ be the amount of interest
And ‘i’ be the rate of interest per unit
Then-
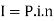
Here- i = r/100
We can calculate the amount as-
Example: Sushmita invested 5000rs. At the rate of 8 per cent per annum then what will be the value of the amount she invested in 5 years.
Sol.
Here P = 5000, i = 8/100 = 0.08, n = 5, now
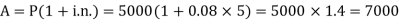
Hence the required amount is - 7000
Example: Find out the simple interest on 5600 rs. At 12 percent per annum from July 15 to September 26, 2020.
Sol.
Here we calculate the time-
Total days from july 15 to sept 26 = 73 days or 73/365 = 1/5 years
And P = 5600, i = 12/100 = 0.12
Simple interest = P.i.n. = 5600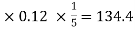 
Hence the simple interest is – 134.40
Example: Harpreet invests 1200rs. At 10 percent per annum for some time and it becomes 1560 then find the principal when that will become 2232 at 8 percent p.a. in the same time.
Sol.
Here in first situation- P = 1200, A = 1560 and i = 0.10
So that,
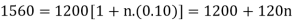
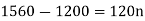
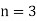
In second situation-
A = 2232, n = 3, i = 0.08
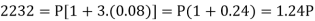
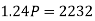
Compound interest-
In compound interest, the principal does not remain same but increases at the end of each interest period.
Let-
P- Principal
A - Amount
i = interest on re. 1 for a year
n = interest period
Then the amount can be calculated as-
And
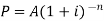
Note- By using algorithm the above formula can be written as-
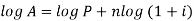
Note- if the compound interest is paid half-yearly, quarterly, monthly instead of a year there will be different formulae as given in the table below-
Time | Amount |
Annually |
|
Half-yearly |
|
Quarterly |
|
Example: Aman invests 1000 rupees at 5 percent p.a for four years then find the compound interest on it.
Sol.
Here P = 1000, i = 0.05 and n = 4
Then we know that-
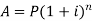
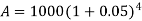
On taking log, we get-
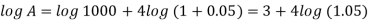
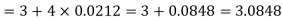
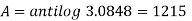
Compound interest will be-
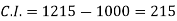
Which is the required answer.
Example:A sum of money invested at C.I. payable yearly amounts to 10, 816 rs. at the end of the second year and to 11,248.64 rs. at the end of the third year. Find the rate of interest and the sum.
Sol.
Here A1 = 10,816, n = 2, and A2 = 11,248.64, n = 3
We know that
A = P (1 + i)n we get,
10,816 =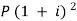 
… (i)
11,248.64 =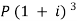
… (ii)
Here on dividing equation (2) by (1)-
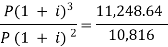
We get-
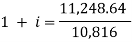
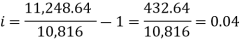
And
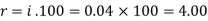
Hence the rate is 4 percent.
Now from first equation-
10,816 =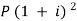 
Or
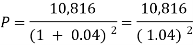
Now-
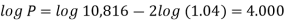
P = antilog 4.000 = 10,000
Therefore they require answer- 10,000
Nominal and effective rate of interest-
Nominal rate of interest is the rate of interest per annum which is compounded yearly, half yearly, quarterly, monthly, n times in a year or continuously.
Effective rate of interest is the rate of interest per annum compounded only once in a year.
There is a relationships between nominal and effective rate of interest under two different conditions-
- If compounding is ‘n’ times in a year-
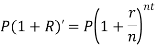
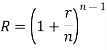
Where ‘r’ is nominal rate and ‘R’ is effective rate.
2. If compounding is continuous-
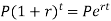
Or
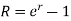
Relationship between two nominal rates-
If interest is compounded quarterly at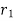 
percent and the interest is compounded half yearly at 
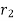percent, then the relationship between the two is-
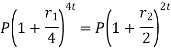
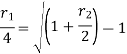
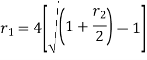
Example: Ronak deposited Rs. 10,000 in a bank for 3 years. Bank gives two offers either 10 percent compounded quarterly or 8% compounded continuously, then which offer is preferable for Ronak?
Sol.
Balance after three years under first offer-
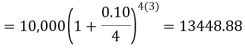
Balance after 3 years under second offer-
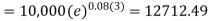
So that we can conclude that the first offer is preferable for Ronak.
Key takeaways-
- Amount- This is the sum of the principal and the interest at any time.
- We calculate the amount as-
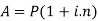
3. Compound interest-
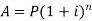
4. Nominal rate- Nominal rate of interest is the rate of interest per annum which is compounded yearly, half yearly, quarterly, monthly, n times in a year or continuously.
5. Effective rate- Effective rate of interest is the rate of interest per annum compounded only once in a year.
6. 
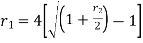
Terms and formulae, problem involving cost price, selling price, trade discount, cash discount
Cost Price (CP) - The price at which an article is purchased.
Selling Price (SP) - This is the price at which an article is sold.
Profit - If the selling price is more than the cost price, then there will be profit
Profit = Selling price (SP) – Cost price (CP)
Profit % = (profit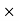
100)/CP
Loss - If the selling price is less than the cost price, then there will be loss
Loss = Cost price (CP) – Selling price (SP)
Loss% = (Loss 
100)/CP
Marked Price - This is the price marked as the selling price on an article, also known as the listed price
Note- Profit or Loss is always calculated on the cost price.
Discount: This is the reduction in price offered on the marked or listed price.
Example: Suppose the profit percentage is 80% of the cost. If the cost further increases by 20% but the selling price remains the same, how much is the decrease in profit percentage?
Sol.
Let us suppose
CP = Rs. 100.
Then Profit = Rs. 80 and selling price = Rs. 180.
The cost increases by 20% → New CP = Rs. 120, SP = Rs. 180.
Profit % = 60/120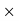 
100 = 50%.
Therefore, Profit decreases by 30%.
Example: A dishonest shopkeeper sells his grocery using weights 15% less than the true weights and makes a profit of 20%. Find his total gain percentage.
Sol.
Suppose 1 kg of grocery bag.
Its actual weight is 85% of 1000 gm = 850 gm.
Let the cost price of each gram be Re. 1. Then the CP of each bag = Rs. 850.
SP of 1 kg of bag = 120% of the true CP
Therefore, SP = 120/100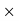 
1000 = Rs. 1200
Gain = 1200 – 850 = 350
Hence Gain % = 350/850 
100 = 41.17%
Example: A shopkeeper offers a discount of 20% on the selling price. On a special sale day, he offers an extra 25% off coupon after the first discount. If the article was sold for Rs. 3600, find the marked price of the article
Sol.
Let the marked price of the article be x.
First a 20% discount was offered, on which another 25% discount was offered.
So, 75% of 80% of x = 3600
75/100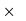 
80/100 
x = 3600 → x = 6000.
So the article was marked at Rs. 6000.
Example: The cost price of 30 articles is equal to the selling price of 40 articles. What is the profit or loss percentage?
Sol.
CP of 30 articles = SP of 40 articles Or, CP/SP = 30/40 =3/4
Or, 1 – CP/SP = 1- 3/4 = 1/4
So, Loss percentage
= (l – CP/SP) x 100 = 1/4x 100 = 25%
Trade discount-
Trade discount is a certain percentage a manufacturer is willing to reduce its list price for wholesalers or retailers.
Trade discounts are given to wholesalers that order large quantities of a product as well as retailers with good relationships with the manufacturer. Purchase discounts or Cash discount are based on payment plans not order quantities.
Trade discounts are offered on bulk purchases by traders, wholesalers, distributors or retailers and not to the end consumers.
Trade discounts are generally offered at varied rates depending on the volume of sale
And
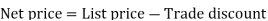
Example: Sweety purchases a set of toys that lists for Rs. 950 and it has a trade discount of 30%, then find the net price.
Sol.
As we know that-
Then
Net price = 950 – 285 = 665
Example: If Raheem will buy a table that lists for Rs. 2000 and it has a trade discount of 50%. Then how much will he pay?
Sol.
As we know that-
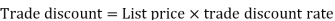
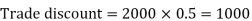
Then
Net price = 2000 – 1000 = 1000
Cash discount is allowed to stimulate instant payment of the goods purchased.
Cash Discount is referred to as a discount, allowed to customers by the seller at the time of making the payment of purchases, as a reduction in the invoice price of the commodity.
Both the buyers and sellers keep a proper record of such discount in their books of accounts.
Sellers offer cash discounts to their buyers as an incentive to encourage early payment.
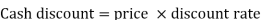
Ordinary dating method-
A credit term of [2/10, n/30] means that you will get a discount of 2% if you clear your account within 10 days
Example: A person received an invoice for Rs. 3,000 dated 22 November 2019 with terms [2/10, n/30]. He paid the whole amount on 30 November 2019. How much did he effectively paid for the bill?
Sol.
5. Date of Invoice: 22nd November 2019
6. Day 1 of the cash discount period. : 23rd November 2019
7. Last day of the Cash discount period: 31st November 2019
8. Date of payment: 30th November 2019
Cash discount.= Price 
Discount rate
= Rs. 3,000 
2/100
= Rs. 60
Amount effectively paid by the person = Bill value - Cash discount
= 3,000 - 60
= Rs. 2,940
Key takeaways-
15. Cost Price (CP) - The price at which an article is purchased
16. Selling Price (SP) - This is the price at which an article is sold
17. Profit = Selling price (SP) – Cost price (CP)
18. Profit = Selling price (SP) – Cost price (CP)
19. Loss = Cost price (CP) – Selling price (SP)
20. Loss% = (Loss 
100)/CP
21. Marked Price - This is the price marked as the selling price on an article, also known as the listed price
22. Discount: This is the reduction in price offered on the marked or listed price.
23. Trade discount is a certain percentage a manufacturer is willing to reduce its list price for wholesalers or retailers.
24. Trade discounts are generally offered at varied rates depending on the volume of sale
25. 
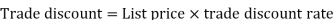
26. 
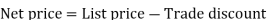
27. 
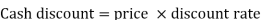
Introduction to commission and brokerage- problems on commission and brokerage
The amount received by the agency for providing its services is known as ‘brokerage’ or ‘commission’.
For example- placement agencies, marriage bureaus etc.
An individual can also run this type of business
Note- An individual who acts as a ‘middle man’ between a seller and buyer is known as broker.
Brokerage is paid by purchaser, Commission is paid by seller. Therefore
Net amount paid by purchaser = Sale price + brokerage
Net amount received by seller = Sale price - commission
Commission % = Commission
100 /Selling price
Selling Price = Commission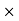
100/ Commission %
Commission (Brokerage) = Commission%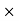
Selling price/100
Example: The Price of a book is Rs. 15.75. A book seller sells 1200 books and pays Rs 17,860.50 to the book publisher after deducting his commission.
Find the commission rate.
Sol.
Here we have total commission,
We have to find the total sale price of books.
The total sale price of books = Number of Books 
Price = 1200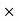
15.75 =18900
Commission = Sale price – Amount paid to the Publisher = 18900-17860.5 = 1039.5
Commission % = Commission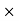
100 /Selling price = 1039.5
100/18900 = 5.5%
Example: Mahesh sold his car for Rs.68,000 with the help of an agent. If the commission paid by Mahesh is Rs 2550. Find rate of commission, and the net amount received by the Mahesh.
Sol.
Commission % = Commission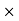
100 /Selling price = 2550
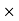100/68000 = 3.75%
Net amount received by farmer = Sale price – Commission = 68000-2550 = Rs65, 450
Example: An agency pays 15% commission to a notebook distributor. The price of each notebook is Rs 3. If he sells 50 copies of notebook every day, find how much commission he receives in a month and also net amount received by the Agency?
Sol.
Price of each newspaper = Rs 3.
Sale price for a day = Number copies sold in day 
price of Cost of news paper = 50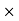
3 = Rs 150
Sale price for a year = Number of days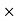
Sale price for a day = 30
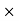150 = 450 Rs
Commission = Commission%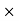
Selling price/100 = 15
450/100 = 67.5 Rs.
Net amount received by agency = selling price – commission = 450 -67.5 = 382.5 Rs
Key takeaways-
- Net amount paid by purchaser = Sale price + brokerage
- Net amount received by seller = Sale price - commission
- Commission % = Commission
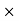100 /Selling price - Selling Price = Commission
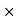100/ Commission % - Commission (Brokerage) = Commission%
Selling price/100
References
- Mathematics and Statistics for Business – R. S. Bhardwaj – Excel Books.
- Business Mathematics and Statistics – Subhanjali Chopra – Pearson publication.
- Fundamentals of Business Mathematics and Statistics – ICAI – ICAI.
- Business Mathematics and Statistics – Dr. J K Das, N Das – McGraw Hill Education.
