Unit - 2
AC Circuits
Representation of sinusoidal waveforms
Peak Value:
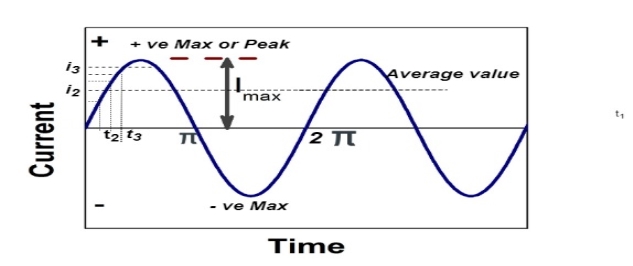
The arithmetic mean of all the value over complete one cycle is called as average value
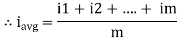
 =
= 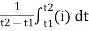
For the derivation we are considering only hall cycle.
Thus  varies from 0 to ᴫ
varies from 0 to ᴫ
i = Im Sin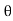
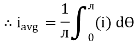
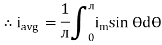
Solving
We get
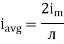
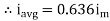
Similarly, Vavg=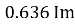
The average value of sinusoid ally varying alternating current is 0.636 times maximum value of alternating current.
RMS value: Root mean square value
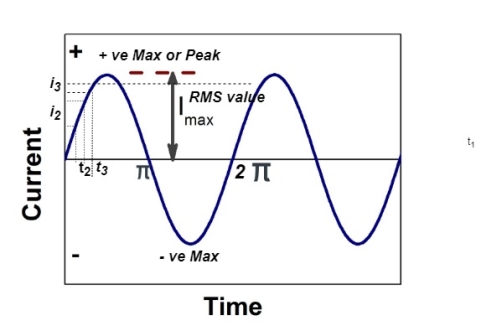
The RMS value of AC current is equal to the steady state DC current that required to produce the same amount of heat produced by ac current provided that resistance and time for which these currents flows are identical.

I rms = 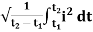
Direction for RMS value:
Instantaneous current equation is given by
i = Im Sin 
But 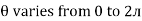
I rms = 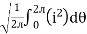
= 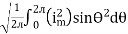
=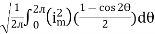
=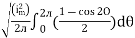
Solving
=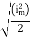
=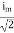
Similar we can derive
V rms= 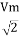 or 0.707 Vm
or 0.707 Vm
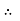 the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
Phasor for Sinusoidal wave
A sinusoidal quantity, i.e. current, i(t) = Imsin(ωt), is taken up as an example. In Fig.a, the length, OP, along the x-axis, represents the maximum value of the current Im, on a certain scale. It is being rotated in the anti-clockwise direction at an angular speed, ω, and takes up a position, OA after a time t (or angle, θ = ωt, with the x-axis). The vertical projection of OA is plotted in the right hand side of the above figure with respect to the angle θ. It will generate a sine wave (Fig.b), as OA is at an angle, θ with the x-axis, as stated earlier. The vertical projection of OA along y-axis is OC = AB = i(θ)=Im sin θ, which is the instantaneous value of the current at any time t or angle θ. The angle θ is in rad., i.e. θ = ω t.
The angular speed, ω is in rad/s, i.e. ω = 2π f, where f is the frequency in Hz or cycles/sec. Thus, i=Im sinθ = Im sinωt = Im 2sinπft.
So, OP represents the phasor with respect to the above current, i. The line, OP can be taken as the rms value I=Im/√2, instead of maximum value, Im. Then the vertical projection of OA, in magnitude equal to OP, does not represent exactly the instantaneous value of I, but represents it with the scale factor of 1/√2=0.707. The reason for this choice of phasor as given above.
Fig 1(a) Phasor for current (b) Waveform
The current can be of the form, i(t)= Im (sinωt −α) as shown in Fig d. The phasor representation of this current is the line, OQ, at an angle, α (may be taken as negative), with the line, OP along x-axis (Fig c). One has to move in clockwise direction to go to OQ from OP (reference line), though the phasor, OQ is assumed to move in anti-clockwise direction as given earlier. After a time t, OD will be at an angle θ with OQ, which is at an angle (θ −α = ωt −α), with the line, OP along x-axis. The vertical projection of OD along y-axis gives the instantaneous value of the current
i=√2 I sin (ωt −α) = Im sin (ωt −α).

Fig 2(c) Phasor of phase shifted sinusoidal current (d) waveform
Key takeaway
V rms=  or 0.707 Vm
or 0.707 Vm
 the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
Real Power: [P]
It is nothing but the actual power being used in a circuit.
P= = I2R Watts
= I2R Watts
Reactive Power: [Q]
It is the function of reactance in the circuit X. Mainly reactive loads are inductor and capacitors. These elements dissipate zero power. These element shows that they dissipate power. This is called as reactive power.
Q= = I2X VAR (volt-Ampere-Reactive)
= I2X VAR (volt-Ampere-Reactive)
Apparent Power: [S]
It is the product of a circuit voltage and current without reference to phase angle. It is the combination of both reactive and real power.
S= = I2Z VA (volt-Ampere)
= I2Z VA (volt-Ampere)
Power factor (P.F.)
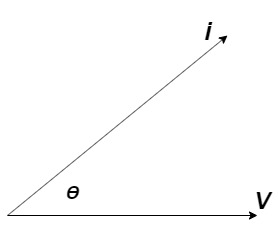
It is the cosine of angle between voltage and current
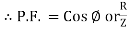
If Ɵis –ve or lagging (I lags V) then lagging P.F.
If Ɵ is +ve or leading (I leads V) then leading P.F.
If Ɵ is 0 or in phase (I and V in phase) then unity P.F.
Ac circuit containing pure resistance (R)
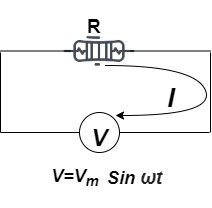
Fig 3 Circuit containing R
Consider Circuit Consisting pure resistance connected across ac voltage source
V = Vm Sin ωt ①
According to ohm’s law i =  =
= 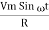
But Im = 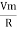
 ②
②
From ① and ② phase or represents RMD value.
phase or represents RMD value.
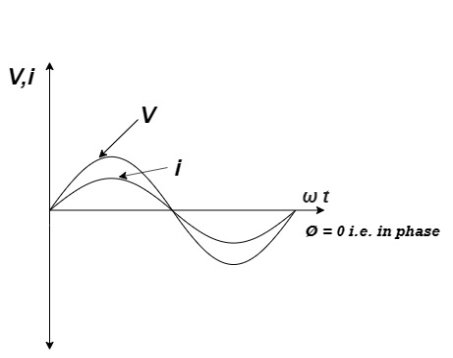
Fig 4 Waveform with element R
Power P = V. i
Equation P = Vm sin ω t Im sin ω t
P = Vm Im Sin2 ω t
P = 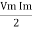 -
- 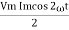
Constant fluctuating power if we integrate it becomes zero

Average power
Pavg = 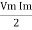
Pavg = 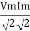
Pavg = Vrms Irms
AC circuit with a pure inductance
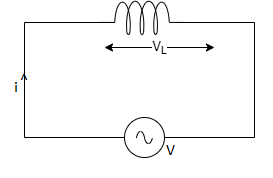
Fig 5 Circuit with pure inductance
Consider an AC circuit with a pure inductance L as shown in the figure. The alternating voltage v is given by
V = Vm Sin ωt
The current flowing in the circuit is i. The voltage across the inductor is given as VL which is the same as v. We can find the current through the inductor as follows
I=L 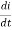
Vm Sin ωt= L 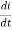
Di= Sin ωt
Sin ωt
i = 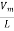

i = 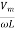 sin (
sin (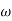 t-
t- )
)
i= im sin (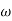 t-
t- )
)
im = 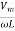
We observe that in a pure inductive circuit, the current lags behind the voltage by 90⁰. Hence the voltage and current waveforms and phasors can be drawn as below
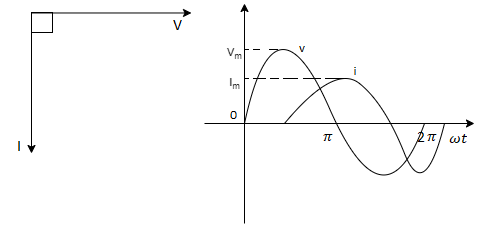
Fig 6 Phasor for Pure L
Inductive reactance
The inductive reactance XL is given as
XL = 2πfL
im = 
AC circuit with a pure capacitance
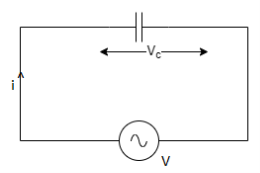
Fig 7 Circuit with pure Capacitance
Consider an AC circuit with a pure capacitance C as shown in the figure. The alternating voltage v is given by
V = Vm Sin ωt
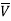 = Vm
= Vm 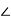 00
00
We can find the current through the capacitor as follows
q=CV
q= Cvm Sin ωt
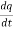 = ωCvm cos(ωt)
= ωCvm cos(ωt)
i= ωCvm cos(ωt)
i=im sin (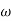 t+
t+ )
)
im= ωCvm
Xc = vm/im = 1/ωC
We observe that in a pure capacitive circuit, the current leads the voltage by 90⁰. Hence the voltage and current waveforms and phasors can be drawn as below.
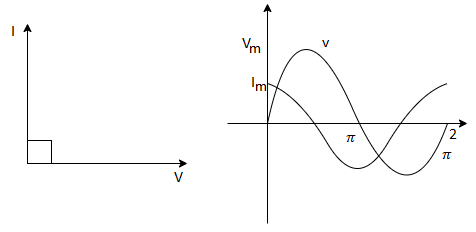
Fig 8 Phasor for C
Capacitive reactance
The capacitive reactance XC is given as
Xc= 1/2πfC
im = vm/Xc
R-L Series Circuit:
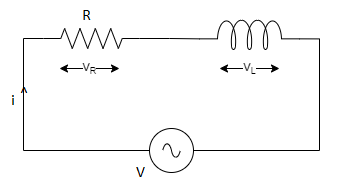
Fig 9 Series RL Circuit
Consider an AC circuit with a resistance R and an inductance L connected in series as shown in the figure. The alternating voltage v is given by
V = Vm Sin ωt
The current flowing in the circuit is i. The voltage across the resistor is VR and that across the inductor is VL
VR=IR is in phase with I
VL=IXL leads current by 90 degrees
With the above information, the phasor diagram can be drawn as shown.

Fig 10 Phasor for RL Circuit
The current I is taken as the reference phasor. The voltage VR is in phase with I and the voltage VL leads the current by 90⁰. The resultant voltage V can be drawn as shown in the figure. From the phasor diagram we observe that the voltage leads the current by an angle Φ or in other words the current lags behind the voltage by an angle Φ. The waveform and equations for an RL series circuit can be drawn as below
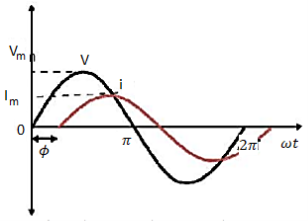
Fig 11 Waveform for R-L circuit
V= Vm Sin ωt
I= Im Sin (ωt-ɸ)
From the phasor diagram, the expressions for the resultant voltage V and the angle Φ can be derived as follows.
V=
VR =IR
VL= IXL
V=I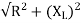
V=IZ
The impedance in an AC circuit is similar to a resistance in a DC circuit. The unit for impedance is ohms(Ω)
Phase angle:
Φ= tan-1
Φ= tan-1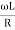
Power Factor:
The power factor in an AC circuit is defined as the cosine of the angle between voltage and current ie., cosΦ
Impedance Triangle: We can derive a triangle called the impedance triangle from the phasor diagram of an RL series circuit as shown
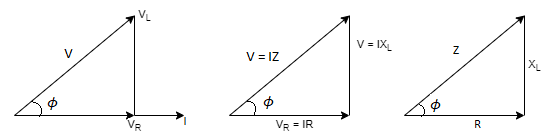
The impedance triangle is right angled triangle with R and XL as two sides and impedance as the hypotenuse. The angle between the base and hypotenuse is Φ. The impedance triangle enables us to calculate the following things.
- Impedance Z=

- Power Factor cosΦ =R/Z
- Phase Angle Φ= tan-1

- Whether current is leading or lagging
RC Series Ciruit
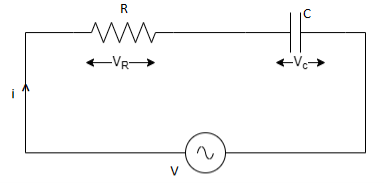
Fig 12 RC Series Circuit
Consider an AC circuit with a resistance R and a capacitance C connected in series as shown in the figure. The alternating voltage v is given by
V= Vm Sin ωt
The current flowing in the circuit is i. The voltage across the resistor is VR and that across the capacitor is Vc
VR=IR is in phase wih I
Vc=IXc lags current by 90 degrees
With the above information, the phasor diagram can be drawn as shown.
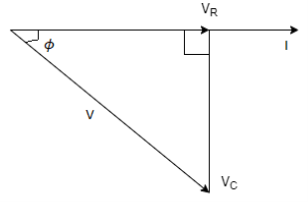
Fig 13 Phasor for RC Circuit
The current I is taken as the reference phasor. The voltage VR is in phase with I and the voltage VC lags behind the current by 90⁰. The resultant voltage V can be drawn as shown in the figure. From the phasor diagram we observe that the voltage lags behind the current by an angle Φ or in other words the current leads the voltage by an angle Φ. The waveform and equations for an RC series circuit can be drawn as below.

Fig 14 Waveform for RC Circuit
V= Vm Sin ωt
I= Im Sin (ωt+ɸ)
From the phasor diagram, the expressions for the resultant voltage V and the angle Φ can be derived as follows.
V=
VR =IR
Vc= IXc
V=I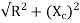
V=IZ
Z= 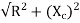
Phase angle
Φ= tan-1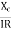
Φ= tan-1

Phasor algebra for RC series circuit.
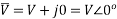
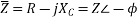
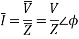
Series RLC circuit
The voltage across inductor = jIXL
Voltage across capacitance = -jIXC
Net voltage across L and C = jI(XL-XC) = j(EL-EC)
Voltage drop across R= IR=ER
Applied voltage E= IR+jI(XL-XC)

Fig 15 Series RLC Circuit
E=I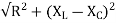
Z=R+j(XL+XC)
Z= 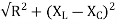
Φ= tan-1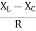
I= 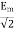
CosΦ= R/Z
Active Power= EI CosΦ
Reactive Power = EI SinΦs
Examples
Q) An alternating current is given by i= 141.4 sin(314t)
Find i) The maximum value ii) Frequency iii) Time Period iv) The instantaneous value when t= 3ms i= 141.4 (314).
A) 
Compare given equation with eq-1.
Maximum value 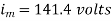
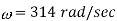
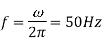
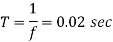
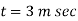
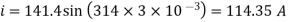
Q) The voltage  is applied to 0.1 H inductor. Find the steady-state current through the inductor.
is applied to 0.1 H inductor. Find the steady-state current through the inductor.
Solution: from equation 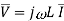
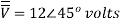
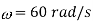
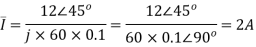
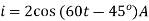
Q) Find equivalent impedance of below circuit.
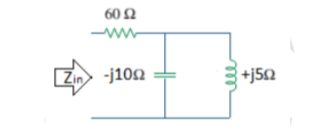
Solution:
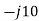 and
and  are in parallel after simplifying
are in parallel after simplifying
Therefore 
Q) Find impedance 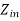 of below circuit.
of below circuit.
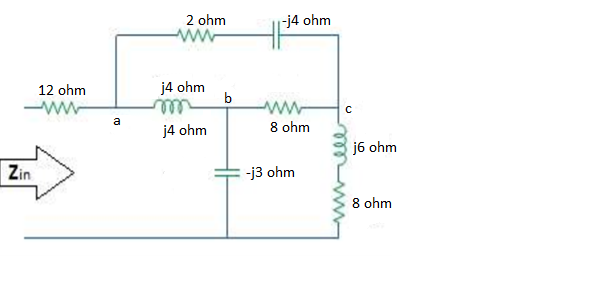
A)
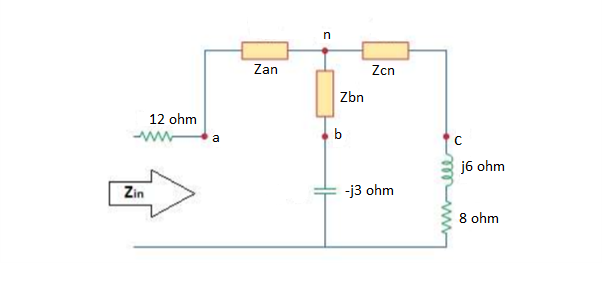
The delta network connected to nodes a, b, and c can be converted to the Y network of fig. We obtain the Y impedances as follows.
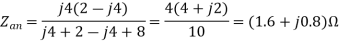
The total impedance at the source terminals is


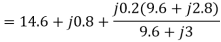
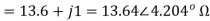
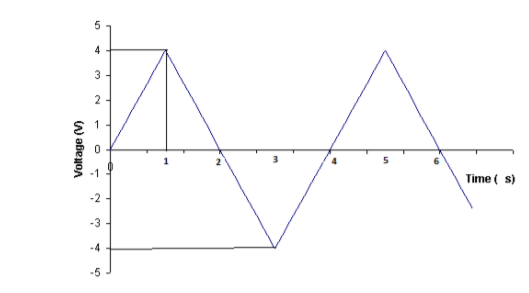
Q) Find form factor of figure factor of figure show below
A)
From figure:
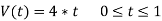
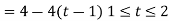
Average value
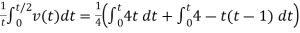
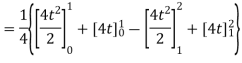

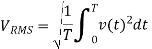
Put T=t/2
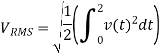
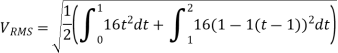
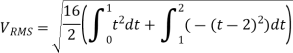
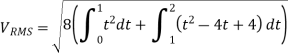
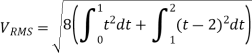
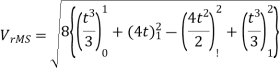


Definition: it is defined as the phenomenon which takes place in the series or parallel R-L-C circuit which leads to unity power factor
Voltage and current in R – L - C ckt. Are in phase with each other
Resonance is used in many communicate circuit such as radio receiver.
Resonance in series RLC series resonance in parallel RLC anti resonance / parallel resonance.
- Condition for resonance XL = XC
- Resonant frequency (Fr): for given values of R-L-C the inductive reactance XL become exactly aqual to the capacitive reactance Xc only at one particular frequency. This frequency is called as resonant frequency and denoted by (fr)
- Expression for resonant frequency(fr): we know thet XL = 2ƛ FL - Inductive reactance
Xc = 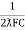 - capacitive reactance
- capacitive reactance
At a particular frequency ȴ = fr, the Inductive and capacitive reactance are exactly equal
 XL = XC ……at ȴ = fr
XL = XC ……at ȴ = fr
Ie 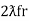 L =
L = 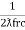
 fr2 =
fr2 = 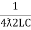
 fr =
fr = 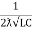 H2
H2
And 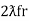 = wr =
= wr =  rad/sec
rad/sec
Quality factor / Q factor
The quality of resonance circuit is measured in terms of efficiency of L and C to stare energy and the efficiency of L and C to store energy as measured in terms of a factor called quality factor or Q factor it is expressed as
Q = 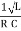 and Q =
and Q = 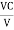
The sharpness of tuning of R-L-C series circuit or its selectivity is measured by value of Q. As the value of Q increases, sharpness of the curve also increases and the selectivity increases.
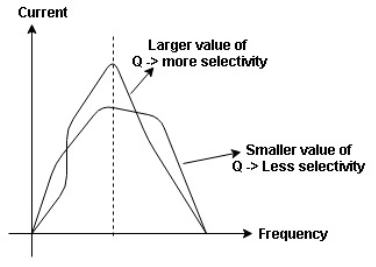
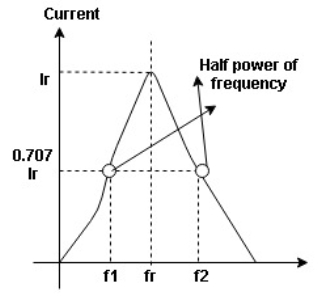
Fig 17 Bandwidth of Resonant Circuit
Bandwidth (BW) = f2 = b1
 and
and 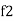 are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance
are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance  these frequency are called as half power frequency
these frequency are called as half power frequency
Bw = fr/Q
Resonance in Parallel circuit:
When a coil is in parallel with a capacitor, as shown below. The circuit is said to be in resonance.
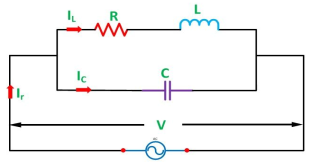
Fig 18 Series RLC circuit
The resonant frequency for above circuit is fr = 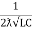 Hz
Hz
The current at resonance is I=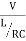
The value L/RC is known as dynamic impedance.
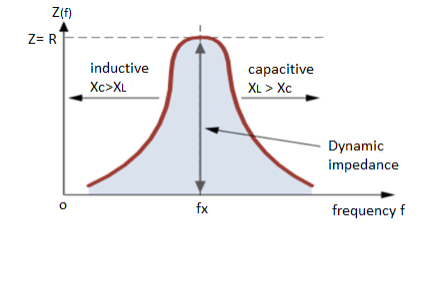
Fig 19 Bandwidth of RLC Circuit
The current at resonance is minimum. The circuits admittance must be at its minimum and one of the characteristics of a parallel resonance circuit is that admittance is very low limiting the circuits current. Unlike the series resonance circuit, the resistor in a parallel resonance circuit has a damping effect on the circuit bandwidth making the circuit less selective.
Also, since the circuit current is constant for any value of impedance, Z, the voltage across a parallel resonance circuit will have the same shape as the total impedance and for a parallel circuit the voltage waveform is generally taken from across the capacitor.
Bandwidth and selectivity:
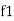 and
and 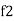 are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance
are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance  thesefrequency are called as half power frequency
thesefrequency are called as half power frequency
Bw = fr/Q
Q = 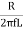 =
= 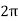 fCR = R
fCR = R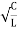
Resonant Frequency:
The resonant frequency for parallel resonant circuit is given as
fR= 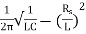
Where L= inductance of the coil
C = is the capacitance
Rs = Resistive value of coil.
Key takeaway
Summary of characteristics of resonant RLC circuits
Characteristic | Series circuit | Parallel Circuit |
Resonant frequency, 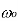 |  | 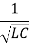 |
Quality factor, Q |  | 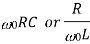 |
Bandwidth B | 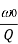 | 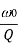 |
Half Power frequencies 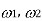 | 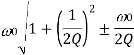 | 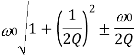 |
For Q 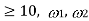 | 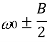 |  |
Examples
Que) A coil takes a current of 6A when connected to 24V dc supply. To obtain the same current with 50HZ ac, the voltage required was 30V. Calculate inductance and p.f of coil?
Sol: The coil will offer only resistance to dc voltage and impedance to ac voltage
R =24/6 = 4ohm
Z= 30/6 = 5ohm
XL = 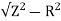
= 3ohm
Cosφ =  = 4/5 = 0.8 lagging
= 4/5 = 0.8 lagging
Que) The potential difference measured across a coil is 4.5V, when it carries a dc current of 8A. The same coil when carries ac current of 8A at 25 Hz, the potential difference is 24V. Find current and power when supplied by 50V,50Hz supply?
Sol: R=V/I= 4.5/8 = 0.56ohm
At 25Hz, Z= V/I=24/8 =3ohms
XL = 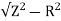
= 2.93ohm
XL = 2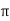 fL = 2
fL = 2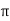 x 25x L = 2.93
x 25x L = 2.93
L=0.0187ohm
At 50Hz
XL = 2x3 =6ohm
Z = 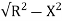 = 5.97ohm
= 5.97ohm
I= 50/5.97 = 8.37A
Power = I2R = 39.28W
Que) A coil having inductance of 50mH an resistance 10ohmis connected in series with a 25 F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
Sol: f0=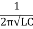 = 142.3Hz
= 142.3Hz
I0 = V/R = 200/10 = 20A
Que) A 15mH inductor is in series with a parallel combination of 80ohm resistor and 20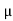 F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
Sol: XL = 2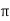 fL = 1000x15x10-3 = 15ohm
fL = 1000x15x10-3 = 15ohm
XL = 1/ C = 50ohm
C = 50ohm
Impedance of parallel combination Z = 80||-j50 = 22.5-j36
Total impedance = j15+22.5-j36 = 22.5-j21
Admittance Y= 1/Z = 0.023-j0.022 siemens
Que) A circuit connected to a 100V, 50 Hz supply takes 0.8A at a p.f of 0.3 lagging. Calculate the resistance and inductance of the circuit when connected in series and parallel?
Sol: For series Z =100/0.8 = 125ohm
Cosφ = 
R = 0.3 x 125 = 37.5ohm
XL =  = 119.2ohm
= 119.2ohm
XL = 2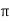 fL = 2
fL = 2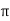 x 50x L
x 50x L
119.2 = 2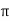 x 50x L
x 50x L
L= 0.38H
For parallel:
Active component of current = 0.8 cosφ = 0.3x0.3 = 0.24A
R = 100/0.24 =416.7ohm
Quadrature component of current = 0.8 sinφ = 0.763
XL= 100/0.763 = 131.06ohm
L= 100/0.763x2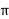 x50 = 0.417H
x50 = 0.417H
Q) A series RLC circuit is connected across a 50Hz supply. R=100, L-159.16mH and C=63.7F. If the voltage across C is 150 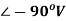 . Find the supply voltage.
. Find the supply voltage.
Solution
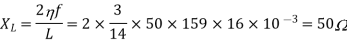
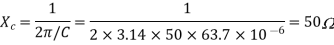
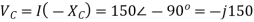

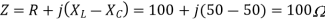
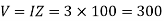
Q) An impedance coil in parallel with a 100µF capacitor is connected across a 200V, 50Hz supply. The coil takes a current of 4A and the power loss in the coil is 600W. Calculate (i) the resistance of the coil (ii) the inductance of the coil (iii) the power factor of the entire circuit.
A) 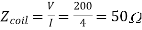

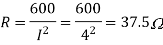
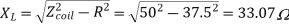
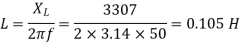
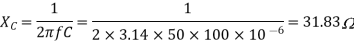
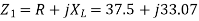
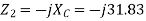
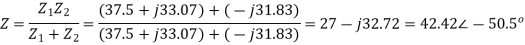
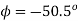
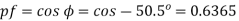
Q) A parallel circuit comprises of a resistor of 20Ω in series with an inductive reactance 15Ω in one branch and a resistor of 30Ω in series with a capacitive reactance of 20Ω in the other branch. Determine the current and power dissipated in each branch if the total current drawn by the parallel circuit is 10∠ −30⁰A?
A)
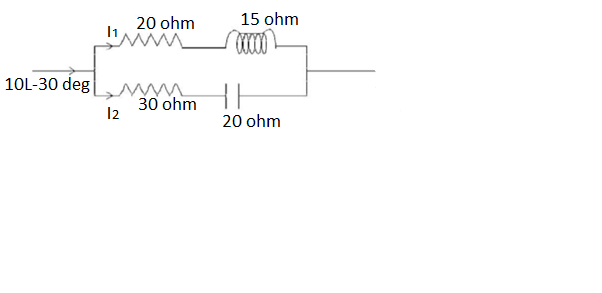

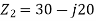
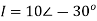
According to KCL
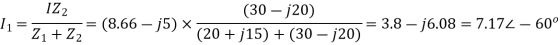

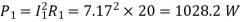

Q) A current of (120-j50)A flows through a circuit when the applied voltage is (8+j12)V. Determine (i) impedance (ii) power factor (iii) power consumed and reactive power.
A)
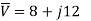
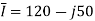
i) 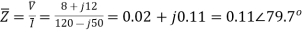
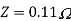
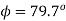
Ii) 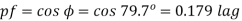
Iii) 
But 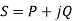
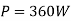
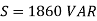
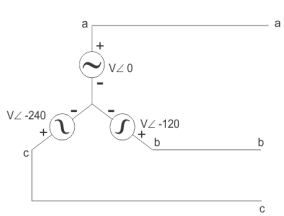
Three phase voltage sources
In three phase the windings are separated by 1200 each. The voltage produced in those windings are 1200 apart from each other. Below shown is one coil RR’ and two more coils YY’ and BB’ each having phase shift of 1200.
The instantaneous value of voltages is given as
VRR’ = Vmsinωt
VYY’ = Vmsin(ωt-120)
VBB’ = Vmsin(ωt-240)
The three phase voltages are of same magnitude and frequency.
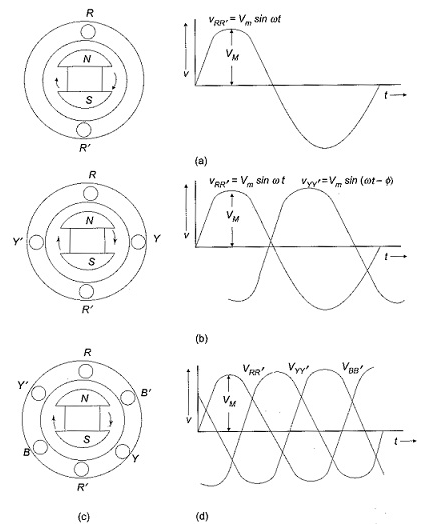
Fig 20 Phase sequence of 3-phase
Phase sequence
The change in voltage is in order VRR’- VYY’- VBB’. So, the three-phase are changed in that order and are called as phase change.
VRR’ = Vmsinωt
VYY’ = Vmsin(ωt-120)
VBB’ = Vmsin(ωt-240)
Phasor Diagram
Consider equation ①
Note: we are getting resultant line current IR by subtracting 2 phase currents IRY and IBR  take phase currents at reference as shown
take phase currents at reference as shown
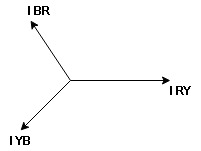
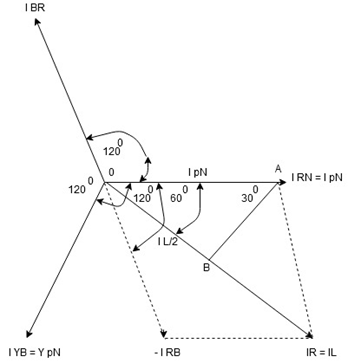
Cos 300 = 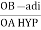
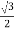 =
= 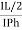
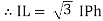
- Complete phases diagram for delta connected balanced Inductive load.

Phase current IYB lags behind VYB which is phase voltage as the load is inductive
- Power relation for delta load star power consumed per phase
PPh = VPh IPh Cos Ø
For 3 Ø total power is
PT= 3 VPh IPh Cos Ø …….①
For star
VL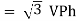 and IL = IPh (replace in ①)
and IL = IPh (replace in ①)
 PT = 3
PT = 3 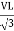 IL Cos Ø
IL Cos Ø
 PT = 3
PT = 3 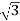 VL IL Cos Ø – watts
VL IL Cos Ø – watts
For delta
VL = VPh and IL = 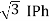 (replace in ①)
(replace in ①)
PT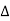 = 3VL
= 3VL 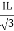 Cos Ø
Cos Ø
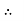 PT
PT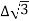 VL IL Cos Ø – watts
VL IL Cos Ø – watts
Total average power
P = 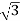 VL IL Cos Ø – for ʎ and
VL IL Cos Ø – for ʎ and 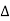 load
load
K (watts)
Total reactive power
Q =  VL IL Sin Ø – for star
VL IL Sin Ø – for star  delta load
delta load
K (VAR)
Total Apparent power
S =  VL IL – for star
VL IL – for star  delta load
delta load
K (VA)
Three phase balanced circuits
Balanced Delta Load
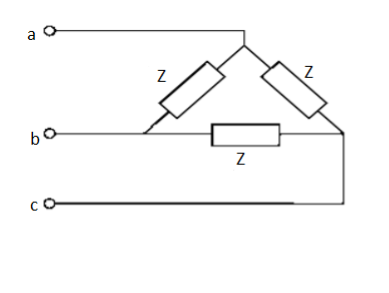
Fig 22 Delta Connection
Let us consider a balanced 3-phase delta connected load Determination of phase voltages:
VAB = V∠00, VBC = V∠-1200, VCA = V∠ − 2400 = V∠1200
Phase current = Phase voltage/ Load impedance
IAB= VAB/Z
IBC= VBC/Z
ICA= VCA/Z
Line currents are calculated by applying KCL at nodes A,B,C
IA = IAB – ICA
IB = IBC - IAB
IC = ICA - IBC
Note: Line currents are also balanced and equal to √3phase current.
Balanced star connected load:
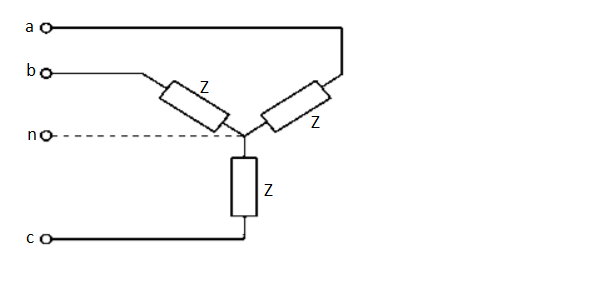
Fig 23 Star Connection
Let us consider a balanced 3-phase star connected load. For star connection,
Phase voltage= Line voltage/(√3)
For ABC sequence, the phase voltage is polar form are taken as
VAN = Vph∠ − 900
VCN = Vph∠1500
VBN = Vph∠300
For star connection line currents and phase currents are equal
IA = VAN/Z
IB = VBN/Z
IC = VCN/Z
To determine the current in the neutral wire, apply KVL at star point IN + IA + IB + IC =0
IN = - (IA + IB + IC) (since they are balanced) In a balanced system the neutral current is zero. Hence if the load is balanced, the current and voltage will be same whether neutral wire is connected or not. Hence for a balanced 3-phase star connected load, whether the supply is 3- phase 3 wire or 3-phase 4 wire, it is immaterial. In case of unbalanced load, there will be neutral current.
Star Connection:
In this type similar ends are connected to common point called as neutral and having a star shape. These connections are used in case of unbalanced current flowing in the three-phase. To avoid any kind of damage we use this connection.
Line voltage VL = Vphase
Vphase
Line current IL = Iphase
Delta Connection:
There are three wires with no neutral. They are used for short distance due to unbalanced current in circuit.

Line voltage VL =Vphase
Line current IL = 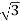 Iphase
Iphase
Examples
Q) Three similar resistors are connected in star across 400V 3-phase lines. Line current is 4A. Calculate the value of each resistor.
Sol: For star connection:
IL=Iph=4A
Vph=VL/ = 400/
= 400/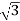 = 231V
= 231V
Rph= 231/4= 57.75ohm
For Delta Connection:
IL=4A
Iph= IL/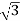
=4/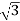 ==2.30A
==2.30A
Zph=400/2.30=173.9ohm
Rph= 173.9/3 = 57.97ohm
Q) Three identical impedances are connected in delta 3-phase supply of 400V. The line current is 30A and total power taken from the supply is 10kW. Calculate the resistance and reactance value of each impedance?
Sol: VL=Vph=400V
IL=30A
Iph=IL/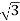 = 30/
= 30/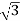 =17.32A
=17.32A
Zph=Vph/Iph= 400/17.32=23.09ohm
P=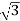 VLILCos Ø
VLILCos Ø
Cos Ø = 10000/ 400x30 = 0.48
400x30 = 0.48
Sin Ø =0.88
Rph=ZphCos Ø= 23.09x0.48=11.08ohm
Xph=ZphSin Ø = 23.09x0.88=20.32ohm
Q) A star connected alternator supplies a delta connected load. The impedance of the load branch is 6+j5 ohm/phase. The line voltage is 230V. Determine the current in the load branch and power consumed by the load.
Sol: Zph= = 7.8ohm
= 7.8ohm
VL=Vph=230V
Iph=Vph/Zph=230/7.8=29.49A
Iph=IL/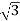
IL=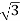 Iph=
Iph=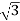 x29.49=51.07A
x29.49=51.07A
P=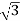 VLIL Cos Ø =
VLIL Cos Ø = 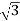 x 230x51.07x0.768=15.62kW
x 230x51.07x0.768=15.62kW
Q) The load connected to a 3-phase supply comprise three similar coils connected in star. The line currents are 25A and the kVA and kW inputs are 18 and 10 respectively. Find the line and phase voltage, the kVAR input resistance and reactance of each coil?
Sol: IL= 25A
P= 10000W
Cos Ø = 10/18 = 0.56
P=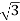 VLIL Cos Ø
VLIL Cos Ø
10000=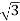 x VLx25x0.56
x VLx25x0.56
VL =412.39V
Vph=VL/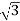 = 412.39/
= 412.39/ =238.09V
=238.09V
KVAR= = 14.96
= 14.96
Zph=238.09/25=9.52ohm
Rph=Zph Cos Ø= 9.52x0.56=5.33ohm
Xph=Zph Sin Ø = 9.52x0.83=7.88ohm
Q) A balanced delta connected load consisting of three coils draws 8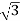 A at 0.5 p.f from 100V 3-phase ac supply. If the coils are reconnected in star across the same supply. Find the line current and total power consumed?
A at 0.5 p.f from 100V 3-phase ac supply. If the coils are reconnected in star across the same supply. Find the line current and total power consumed?
Sol: For Delta connection:
IL=8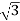 A
A
Iph= IL/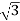 = 8A
= 8A
Vph=100V
Zph=100/8=12.5ohm
Rph=Zph Cos Ø=12.5x0.5 = 6.25ohm
Xph=Zph Sin Ø = 12.5x0.866=10.825ohm
P=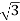 VLIL Cos Ø
VLIL Cos Ø
= 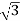 x 100x 8
x 100x 8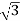 x0.5=1200W
x0.5=1200W
For Star Connection:
Vph= VL/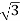 = 100/
= 100/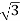 V=57.73V
V=57.73V
Zph=100/8=12.5ohm
Iph=57.73/12.5=4.62A
P=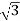 VLIL Cos Ø
VLIL Cos Ø
=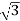 x 100x 4.62x0.5
x 100x 4.62x0.5
P= 400W
References:
- D. P. Kothari and I. J. Nagrath, “Basic Electrical Engineering”, Tata McGraw Hill, 2010.
- D. C. Kulshreshtha, “Basic Electrical Engineering”, McGraw Hill, 2009.
- L. S. Bobrow, “Fundamentals of Electrical Engineering”, Oxford University Press, 2011.
- E. Hughes, “Electrical and Electronics Technology”, Pearson, 2010.
- V. D. Toro, “Electrical Engineering Fundamentals”, Prentice Hall India, 1989.