Unit - 4
Magnetic Forces
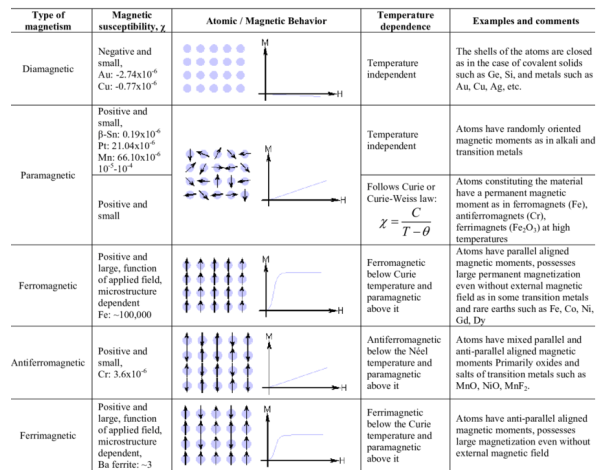
A material is magnetically characterized based on the way it can be magnetized. This depends on the material’s magnetic susceptibility – its magnitude and sign.
Three basic magnetisms are:
- Dia-magnetism
- Para-magnetism
- Ferro-magnetism.
- Anti-ferro-magnetism and ferri-magnetisms are considered as subclasses of ferro-magnetism.
Dia-magnetism
- Very weak; exists ONLY in presence of an external field, non-permanent.
- Applied external field acts on atoms of a material, slightly unbalancing their orbiting electrons, and creates small magnetic dipoles within atoms which oppose the applied field. This action produces a negative magnetic effect known as diamagnetism.
- The induced magnetic moment is small, and the magnetization (M) direction is opposite to the direction of applied field (H).
- Thus, the relative permeability is less than unity i.e. magnetic susceptibility is negative, and is in order of -10-5.
- Materials such as Cu, Ag, Si, Ag and alumina are diamagnetic at room temperature.
Para-magnetism
- Slightly stronger; when an external field is applied dipoles line-up with the field, resulting in a positive magnetization. However, the dipoles do not interact.
- Materials which exhibit a small positive magnetic susceptibility in the presence of a magnetic field are called para-magnetic, and the effect is termed as para-magnetism.
- In the absence of an external field, the orientations of atomic magnetic moments are random leading to no net magnetization.
- When an external field is applied dipoles line-up with the field, resulting in a positive magnetization.
- However, because the dipoles do not interact, extremely large magnetic fields are required to align all of the dipoles.
- In addition, the effect is lost as soon as the magnetic field is removed.
- Since thermal agitation randomizes the directions of the magnetic dipoles, an increase in temperature decreases the paramagnetic effect.
- Para-magnetism is produced in many materials like aluminium, calcium, titanium, alloys of copper. Magnetic susceptibility of these materials is slightly positive, and lies in the range +10-5 to +10-2.
Ferro-magnetism
- Both dia- and para- magnetic materials are considered as non-magnetic because they exhibit magnetization only in presence of an external field.
- Certain materials possess permanent magnetic moments even in the absence of an external field.
- This is result of permanent unpaired dipoles formed from unfilled energy levels.
- These dipoles can easily line-up with the imposed magnetic field due to the exchange interaction or mutual reinforcement of the dipoles. These are chrematistics of ferromagnetism.
- Materials with ferro-magnetism (Examples: Fe, Co, Ni, Gd) possess magnetic susceptibilities approaching 106.
- Above the Curie temperature, ferro-magnetic materials behave as para-magnetic materials and their susceptibility is given by the Curie-Weiss law, defined as
χm = C/T-TC
Where C – material constant, T – temperature, Tc – Curie temperature.
Anti-ferro-magnetism
- Dipoles line-up, but in opposite directions, resulting in zero magnetization.
- Eg: Mn, Cr, MnO, NiO, CoO, MnCl2
- Exchange interaction which is responsible for parallel alignment of spins is extremely sensitive to inter-atomic spacing and to the atomic positions. This sensitivity causes anti-parallel alignment of spins.
- When the strength of anti-parallel spin magnetic moments is equal, no net spin moment exists, and resulting susceptibilities are quite small.
- One noticeable characteristic of anti-ferro-magnets is they attain maximum susceptibility at a critical temperature called Neel temperature. At temperatures above this, anti-ferro-magnets become para-magnetic.
Ferri-magnetism
- Some ceramic materials exhibit net magnetization.Eg: Fe3O4, NiFe2O4, (Mn.Mg)Fe2O4, PbFe12O19, Ba Fe12O19, YIG – yttrium iron garnet Y3Fe5O12.
- In a magnetic field, the dipoles of a cation may line up with the field, while dipoles of other cation may not. These ceramics are called ferrites, and the effect is known as ferri-magnetism.
- Ferri-magnetism is similar to anti-ferro-magnetism in that the spins of different atoms or ions line up anti-parallel. However, the spins do not cancel each other out, and a net spin moment exists.
- Below the Neel temperature, therefore, ferromagnetic materials behave very much like ferromagnetic materials and are paramagnetic above the Neel temperature.
- These materials exhibit a large but field dependent magnetic susceptibility similar to ferro-magnets.
- They also show Curie-Weiss behavior. As these ceramics are good insulators, electrical losses are minimal, and hence ferrites have lot of applications in devices such as high frequency transformers.
Key takeaway
It is the force exerted on the charged particle q moving with velocity v through an electric field E and magnetic field B. The entire electromagnetic force F on the charged particle is called Lorentz force which is given by
F = qE + qv x B ---------------------(1)
The first term indicates electric field. The second term indicates magnetic force which has direction perpendicular to both velocity and magnetic field.
The magnetic force is proportional to q and to the magnitude of the vector cross product v × B. In terms of the angle ϕ between v and B, the magnitude of the force equals qvB sin ϕ.
If v is perpendicular to B the particle will follow circular trajectory with radius of r = mv/qB. If the angle ϕ is less than 90°, the particle orbit will be a helix with an axis parallel to the field lines.
If ϕ is zero, there will be no magnetic force on the particle, which will continue to move undeflected along the field lines.
When a conductor is placed with B field perpendicular to current, the magnetic force on both types of charge carriers is in the same direction. This force gives rise to small potential difference between the sides of the conductor.
If a wire with a current i is placed in an external magnetic field B, Since, current represents movement of charges in the wire, the Lorentz force acts on the moving charges. Because these charges are bound to the conductor, the magnetic forces on the moving charges are transferred to the wire.
The force on a small length dl of the wire depends on the orientation of the wire with respect to the field. The magnitude of the force is given by I dlB sin ϕ, where ϕ is the angle between B and dl. There is no force when ϕ = 0 or 180°, both of which correspond to a current along a direction parallel to the field. The force is at a maximum when the current and field are perpendicular to each other. The force is given bydF= idl × B.
Magnetic field intensity (H)
The Magnetic Field Intensity or Magnetic Field Strength is a ratio of the MMF needed to create a certain Flux Density (B) within a material per unit length of that material.
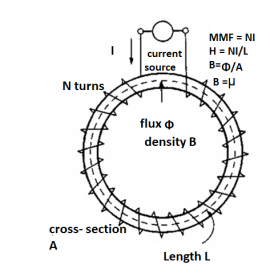
H = At/m, ampere-turns per meter. N is used as the number of turns of wire around a core or magnetic material. So, H = N*I/m.
This is the horizontal axis of the B-H curve for magnetic materials, and is used to vary the magnetic flux within the material by varying the current in the solenoid, thus varying the At (varying the amperes of the ampere-turns).
To determine the B-H curve of a material, the H is varied by controlling the magnitude and polarity of the current flowing in the coil around the sample material, and B is measured.
Arrange a loop of wire so that the magnetic field pushes one way on one side and the other way the opposite side.

The current through a coil of wire immersed in a magnetic field causes magnetic force to spin the coil. Every loop of current and direction associated with it is perpendicular to the plane of the loop in the direction that right thumb would point if right fingers curled around the coil.

The magnetic force on a current carrying loop tries to align the loops normal vector with the magnetic field.
Suppose a magnetic field runs left to right then
The result of a push one way on one side of the coil and a push the other way on the other side is a torque an entity that causes the coil to spin.
The larger the torque the more resistance to spinning can be overcome. The torque on a coil of current carrying wire
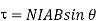
Where
N= no of loops of wire in the coil.
I = current through coil
A = area of coil.
B = magnetic field strength (Tesla)
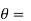 angle between magnetic field and normal to coil.
angle between magnetic field and normal to coil.

Magnetic moment
The magnetic moment is a vector relating torque of an object to the magnetic field. This is mathematically represented as:
τ = m × B
Where,
τ is the torque acting on the dipole
m is the magnetic moment
B is the external magnetic field
In the definition for the current loop, the Magnetic moment is the product of the current flowing and the area, M = I A
So, the unit conferring to this definition is articulated by Amp-m2.
It can also be suggested in terms of torque and moment. Conferring to that, the torque is measured in Joules (J) and the magnetic field is measured in tesla (T) and thus the unit is J T -1.
So, these two units are equivalent to each other and are provided by 1 Amp-m2 = 1 J T -1.
A Magnetic Dipole comprises two unlike poles of equivalent strength and parted by a small distance. For instance: The needle of a compass, a bar magnet, etc. are magnetic dipoles. We shall show that a current loop works as a magnetic dipole.
Magnetic Dipole Moment is described as the product of pole strength and the distance amidst the two poles. The distance between the two poles of a magnetic or a magnetic dipole is named as the magnet length and is given as the 2L.
A magnetic dipole, generally a tiny magnet of microscopic to subatomic dimensions, equivalent to a flow of electric charge around a loop. Electrons circulating around atomic nuclei, electrons spinning on their axes, and rotating positively charged atomic nuclei all are magnetic dipoles. The sum of these effects may cancel so that a given type of atom may not be a magnetic dipole. If they do not fully cancel, the atom is a permanent magnetic dipole, as are iron atoms. Many millions of iron atoms spontaneously locked into the same alignment to form a ferromagnetic domain also constitute a magnetic dipole. Magnetic compass needles and bar magnets are examples of macroscopic magnetic dipoles.
The strength of a magnetic dipole, called the magnetic dipole moment, may be thought of as a measure of a dipole’s ability to turn itself into alignment with a given external magnetic field. In a uniform magnetic field, the magnitude of the dipole moment is proportional to the maximum amount of torque on the dipole, which occurs when the dipole is at right angles to the magnetic field. The magnetic dipole moment, often simply called the magnetic moment, may be defined then as the maximum amount of torque caused by magnetic force on a dipole that arises per unit value of surrounding magnetic field in vacuum.
When a magnetic dipole is considered as a current loop, the magnitude of the dipole moment is proportional to the current multiplied by the size of the enclosed area. The direction of the dipole moment, which may be represented mathematically as a vector, is perpendicularly away from the side of the surface enclosed by the counter clock wise path of positive charge flow. Considering the current loop as a tiny magnet, this vector corresponds to the direction from the south to the north pole. When free to rotate, dipoles align themselves so that their moments point predominantly in the direction of the external magnetic field. Nuclear and electron magnetic moments are quantized, which means that they may be oriented in space at only certain discrete angles with respect to the direction of the external field.
Each orbit consists of electrons which orbit the central positive nucleus. The electrons also rotate about their own axes. Thus, an internal magnetic field is produced by electrons orbiting around the nucleus as in Figure 10 (a) or electrons spinning as in Figure (b). Both these electronic motions produce internal magnetic fields Bi that are like the magnetic field produced by a current loop of Figure. The equivalent current loop has a magnetic moment of m = IbSan, where S is the area of the loop and Ib is the bound current (bound to the atom).

Figure: (a) Electron orbiting around the nucleus (b) Electron Spin
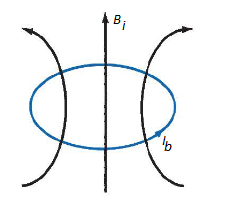
Figure: Circular current loop equivalent to electronic motion of electron
Without an external B field applied to the material, the sum of m, s is zero due to random orientation as in Figure 12(a). When an external B field is applied, the magnetic moments of the electrons more or less align themselves with B so that the net magnetic moment is not zero, as illustrated in Figure 12(b).
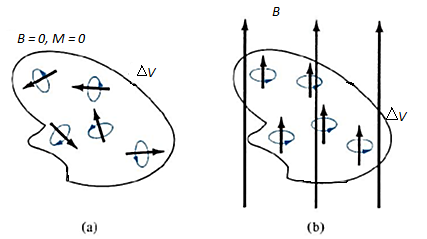
Figure: Magnetic dipole moment in a volume  : (a) before B is applied (b) after B is applied.
: (a) before B is applied (b) after B is applied.
To derive normal and tangential boundary conditions for magnetostatics:
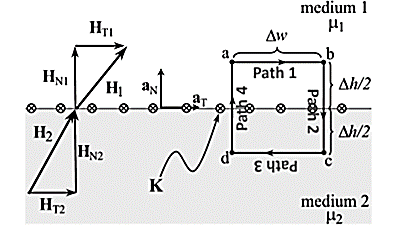
According to Ampere’s circuit law:
 dL = I enc
dL = I enc
The current enclosed by the path is

Break H into four Integrals
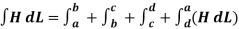 =Kw
=Kw
Path 1: =
=  T1 a T dL a T = H T1
T1 a T dL a T = H T1
Path 2:  N1 aN dL aN +
N1 aN dL aN +  N2 aN dL aN = -(HN1 + HN2)
N2 aN dL aN = -(HN1 + HN2) 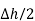
Path 3: 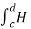 dL =
dL = 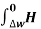 T2aT dLaT= -HT2
T2aT dLaT= -HT2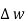
Path 4: 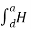 dL =
dL =  N2dL aN+
N2dL aN+ 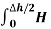 N1 a NdL aN = (H N1 + H N2)
N1 a NdL aN = (H N1 + H N2) 
Combing the results, we get
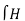 dL = Ienc
dL = Ienc
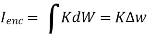
Tangential BC = HT1 – HT2 = K
A more general expression for the first magnetostatic boundary condition can be written as

Where a21 is a unit vector normal going from media 2 to media 1.

Gauss’s Law for Magnetostatic fields:
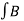 ds = 0
ds = 0
To find the second boundary condition, we center a Gaussian pillbox across the interface as shown in Figure.
We can shrink h such that the flux out of the side of the pillbox is negligible.
Then we have

For normal BC
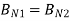
Thus, we see that the normal component of the magnetic flux density must be continuous across the boundary.
B N1 = B N2
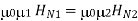
We can say that
H N1 ≠ H N2
Problem:
The magnetic field intensity is given as H1 = 6ax + 2ay + 3az (A/m) in a medium with mr1 = 6000 that exists for z < 0. We want to find H2 in a medium with mr2 = 3000 for z >0.

Step (a) and (b): The first step is to break H1 into its normal component (a) and its tangential component (b).
Step (c): With no current at the interface, the tangential component is the same on both sides of the boundary.
Step (d): Next, we find BN1 by multiplying HN1 by the permeability in medium 1.
Step (e): This normal component B is the same on both sides of the boundary.
Step (f): Then we can find HN2 by dividing BN2 by the permeability of medium 2.
Step (g): The last step is to sum the fields.
Consider two stationary loops of wire, labeled 1 and 2—see Figure. Let us run a steady current I1 around the first loop to produce a magnetic field B1. Some of the field-lines of B1 will pass through the second loop. Let Φ2 be the flux of B1 through loop 2

Where dS2 is a surface element of loop 2. This flux is generally quite difficult to calculate exactly (unless the two loops have a particularly simple geometry). However, we can infer from the Biot-Savart law,
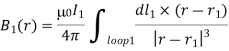
That the magnitude of B1 is proportional to the current I1. This is ultimately a consequence of the linearity of Maxwell’s equations. Here, dl1 is a line element of loop 1 located at position vector r1.
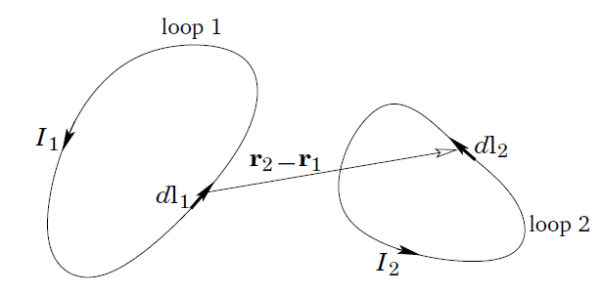
It follows that the flux Φ2 must also be proportional to I1. Thus, we can write
Φ2 = M21 I1,
Where M21 is a constant of proportionality. This constant is called the mutual inductance of the two loops.
Let us write the magnetic field B1 in terms of a vector potential A1, so that
B1 = ∇×A1.
It follows from Stokes’ theorem that

Where dl2 is a line element of loop 2. However, we know that
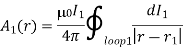
The above equation is just a special case of the more general law,

For j(r1) = dl1 I1/dl1 dA and d3r _ = dl1 dA, where dA is the cross sectional area of loop 1. Thus,

Where r2 is the position vector of the line element dl2 of loop 2, which implies that

In fact, mutual inductances are rarely worked out using the above formula, because it is usually much too difficult. However, this expression— which is known as the Neumann formula—tells us two important things. Firstly, the mutual inductance of two current loops is a purely geometric quantity, having to do with the sizes, shapes, and relative orientations of the loops. Secondly, the integral is unchanged if we switch the roles of loops 1 and 2. In other words,
M21 = M12.
Hence, we can drop the subscripts, and just call both these quantities M.
This is a rather surprising result. It implies that no matter what the shapes and relative positions of the two loops, the magnetic flux through loop 2 when we run a current I around loop 1 is exactly the same as the flux through loop 1 when we run the same current around loop 2.
We have seen that a current I flowing around some wire loop, 1, generates a magnetic flux linking some other loop, 2. However, flux is also generated through the first loop. As before, the magnetic field, and, therefore, the flux, Φ, is proportional to the current, so we can write
Φ = L I.
The constant of proportionality L is called the self-inductance. Like M it only depends on the geometry of the loop. Inductance is measured in SI units called henries (H): 1 henry is 1 volt-second per ampere. The henry, like the farad, is a rather unwieldy unit, since inductors in electrical circuits typically have inductances of order one micro-henry.
As magnetic field is generated by electric currents the magnetic energy is an energy form of moving charge carrier electrons. Magnetism is described by magnetic fields. These are caused by magnetic materials (e.g., permanent magnets), electric currents (e.g., current-carrying coils), or a temporary change in the electric field. Magnetic field lines indicate the magnetic flux. As with the earth's magnetic field, magnets (e.g., bar magnets) have north and south poles, the former always aligning in the direction of the Arctic magnetic pole. Since work is done to generate a magnetic field, the field has energy in a magnetic energy store.
Depending on the material, the amount of magnetic energy may be different. The hysteresis describes this connection. Again, those effects are described by the Maxwell equations, which indicate why electrical charge carriers generate magnetic fields.

The energy is also given as
E=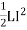
Examples
Que)The amount of flux present in around magnetic bar was measured at 0.013 weber. If the material has a diameter of 14cm, calculate the flux density.
Sol: Area=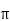 r2
r2
Diameter=2r
r=14/2=7cm=0.07m
Area=3.14 x 0.072=0.0154m2
Flux Density B== A=0.013/0.0154=0.843 Tesla
A=0.013/0.0154=0.843 Tesla
Que) Calculate the radius of the material having flux density of 0.5 T and flux present around the magnetic bar is 0.02T.
Sol: Flux Density B= A
A
A= 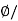 B=0.02/0.5=0.04 m2
B=0.02/0.5=0.04 m2
Area=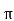 r2
r2
r=0.113m
Que) A wire 2.5m long is bent into a square and into a circle. If the current flowing through the wire is 100 A, find the magnetising force at the centre of the square and the centre of the circle?
Sol: Value of h at centre of square will be H= =
=  =144 AT/m
=144 AT/m
Value of H at the centre of circle is H=I/2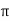 r
r
=125.6AT/m
Que) Calculate the magnetising force and flux density at a distance of 4cm from a long straight circular conductor carrying a current of 250A and placed in air?
Sol: H=I/2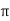 r
r
=250/2 x 0.04=994.71 AT/m
x 0.04=994.71 AT/m
B= μoH
=4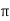 x10-7x994.71=1.25x10-3 Wb/m2
x10-7x994.71=1.25x10-3 Wb/m2
Q) Find the H field within the slab when it is (a) permanently magnetized with magnetization Moi, (b) a linear permeable material with permeability A.
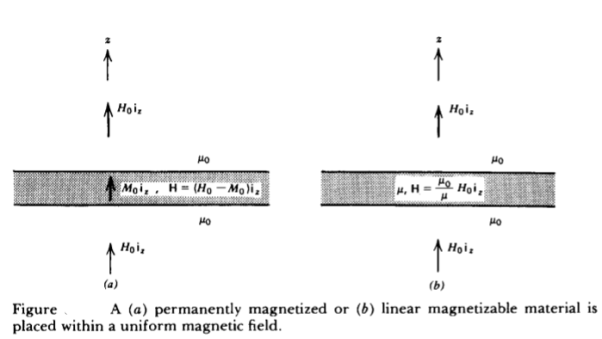
A) For both cases, requires that the B field across the boundaries be continuous as it is normally incident. (a) For the permanently magnetized slab, this requires that
 oH0 =
oH0 =  o(H+M0)
o(H+M0)
H=H0-M0
Note that when there is no externally applied field (Ho = 0), the resulting field within the slab is oppositely directed to the magnetization so that B = 0.
(b) For a linear permeable medium requires
 oH0 =
oH0 =  o(H)
o(H)
H= 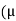 o/
o/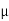 ) H0
) H0
For  >
>  o the internal magnetic field is reduced. If H0 is set to zero, the magnetic field within the slab is also zero.
o the internal magnetic field is reduced. If H0 is set to zero, the magnetic field within the slab is also zero.
References:
1. WH Hayt and JA Buck, “Engineering Electromagnetic”, McGraw- Hill Education.
2. Antenna and wave propagation by k.d parsad satya prakashan.