Unit - 7

Introduction and Classification of filters and its uses

7.1 Introduction and Classification of filters and its uses

Filters are those electrical circuits which perform signal processing functions, to remove unwanted frequency components.

[I]. Classification of Passive Filters

Passive filters are made up of passive components such as resistors, capacitors and inductors, and have no amplifying elements such as transistors, op-amps etc. so have no signal gain. Therefore, the output level is always less than the input.

Filters are so named according to the frequency range of signals that they allow to pass.

(a) Low Pass Filter:-These filters reject all frequencies above a specified value called the cut off frequency.

(b). High Pass Filter:-These filters rejects all frequencies below the cut off frequency.

(c). Band Pass Filter:-These filters allows signals falling within a certain frequency band and blocks all the frequencies outside this band.

(d). Band Stop Filter:-These filters reject transmission of a limited band of frequencies but allows the transmission of all other frequencies.

The figure below gives the ideal gain v/s frequency response of above all mentioned types of filters.

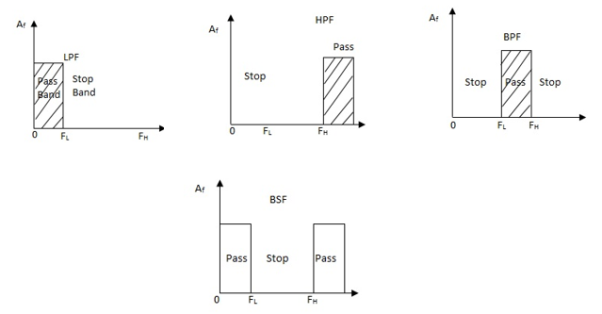
A BPF is usually obtained by series connections of LPF with a HPF, where FL of HPF < FH of LPF.

A BSP may be obtained by parallel connections of LPF with a HPF, where FH of HPF  > FL of LPF.

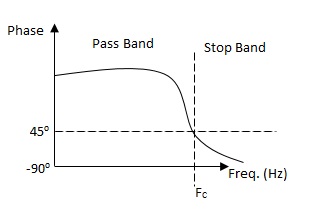
Frequency response

For RC LPF the reactance of ‘ C ’ is very high at low frequency so, capacitor acts as open circuit and blocks i/p signal Vi until cut-off frequency is reached.

Cut-off frequency for a LPF is that frequency at which the voltage at output equals 70.7% of input voltage( -3 dB point ).

LPF are used to filter noise from circuit.

Q –A LPF circuit consisting of a resistor of 40KΩ in series with capacitor 47nF across a 10V sinusoidal supply. Calculate VO at frequency 1Kz?

Sol:

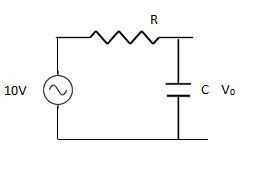
R = 40KΩ

C = 47nF

Vi = 10V

F = 1000 Hz

For LPF,

Capacitive Reactance is XC

The output voltage is given as

VO = Vi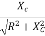

XC = =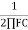

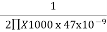
XC = 3.386KΩ

VO =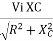

=10 x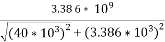

= 10 x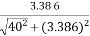

VO = 0.843 V

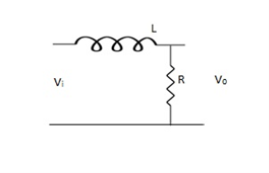
(b) RL LPF

FC = R / 2nt

VO = Vi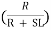

Characteristic impedance of low pass

A Basic LPF circuit can be designed using passive elements R, L and C. The circuit is having single ‘ R ’ in series with capacitor ‘C’.

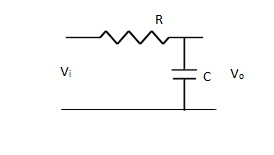
For RC LPF

VO = = Vi x 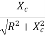fC = 1 / 2∏RC

But Z = 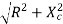             Phase shift φ = -cot(2∏FC)

And XC =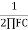

VO – output voltage

Vi – input voltage

Z – Impedance

XC – Capacitive Reactance

FC – cut off Frequency

For RC LPF the reactance of ‘ C ’ is very high at low frequency so, capacitor acts as open circuit and blocks i/p signal Vi until cut-off frequency is reached.

Cut-off frequency for a LPF is that frequency at which the voltage at output equals 70.7% of input voltage( -3 dB point ).

LPF are used to filter noise from circuit.

Comparison of RL – RC circuits

• RC circuit occupy small space. It is not possible to fabricate inductors on surface of semiconductor chip.
• The response of charging and discharging of RL circuit is not proper.
• Capacitors are less expensive.
• RC- circuit is used in high time constant application. While RL used in low time constant applications.

Q – An RL LPF consists of 5.6mH coil a 3.3 KΩ resistor. The output voltage is taken across resistor. Calculate the critical frequency?

Sol: Given:

L = 5.6 x 10-3 H

R = 3.3 x 103Ω

For RL LPF

F ==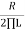

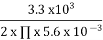
F = 93.78 KHz

Q – A sinusoidal voltage with peak to peak value of 10 V is applied to an RC LPF. If reactance at input is zero, find output voltage?

Sol:

VO =

XC =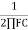

F =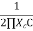                   XC  = 0, F ->∞

Hence, VO = 0V.

Q. An RC – LPF consists of 120 Ω resistor and 0.02 µF capacitor. The output is taken through capacitor. Calculate the critical frequency?

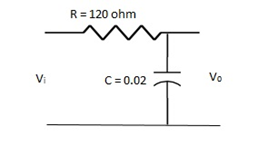
For RC LPF FC is given as

FC==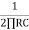

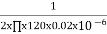
FC = 66.31 KHz

High pass

(a). The RC – HPF circuits is shown below, which is having capacitor at input and resistor at output.

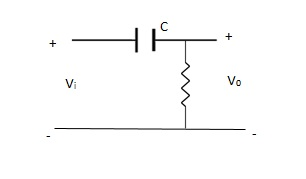
Reactance of capacitor is very high at low frequency.

XC =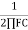

XC  when F   ( C acts as open circuit )

XC   when F   ( C acts as short circuit )

FC =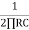

Phase shift = Cot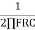

VO =Vi

VO = Vi

At low F: XC ->∞      VO = 0

At high F: XC -> 0      VO = Vi

Q. An RC HPF with input capacitor 10nf and the output resistor of 10K Ω. Find the cut off frequency.

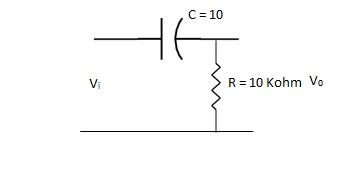
Sol:

FC = =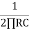

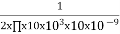
FC = 15.915 Hz

Q. Calculate the break point (FC) for a simple passive HPF consisting of 82pF capacitor connected in series with 240 KΩ resistor?

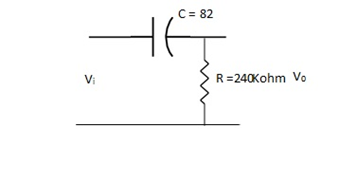
Sol:

FC = =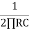

FC = 8KHz

(b). RL – HPF:

The basic RL HPF is shown below. The inductors pass low frequency signals with very little resistance, and offers great resistance to high frequency signals.

VO =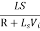

FC =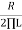

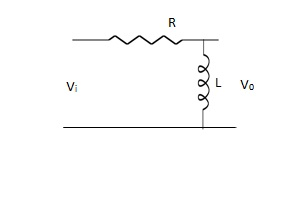
Q. For a RL HPF consists of 470Ω resistor and 600 mH coil output is taken across coil. Calculate the cut off frequencies.

Sol:

FC = 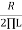==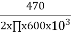 125 Hz 

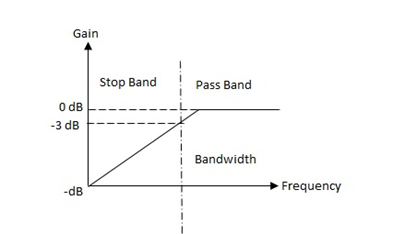
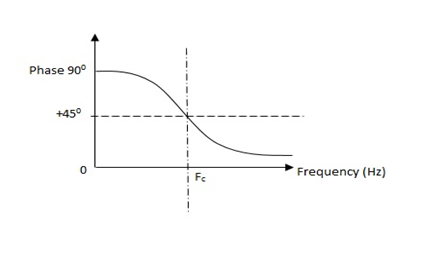
Band Pass and Band reject proto- type section

It can be designed by making a series connection of HPF with a LPF. The Basic circuit is shown below.

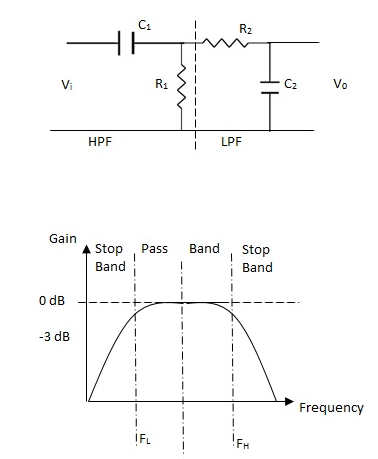
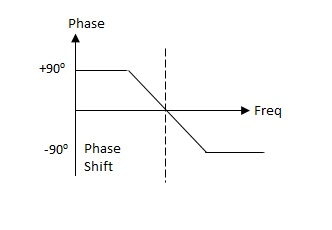
Fig. Frequency response and phase shift Put

FC = 1 / 2∏RC C2 = 1 / 2∏FHR

C1 = 1 / 2∏FLR FR =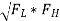

FL = lower -3dB cut off frequency

FH= upper -3dB cut off frequency

Band width (BW) = FH - FL

USES

1>. The BPF has its applications in wireless communication at transmitter and receiver.

2>. It is also used in optical communication.

3>. For reducing the signal to noise ratio at the receiving end.

Q. The value of capacitor C1 required to give a cut off frequency fL = 1KHz and value of resistor is 10K for the BPF. The value of capacitor C2 and higher cut off frequency (FH) is 30 KHz with resistor 10KΩ. Also calculate the central resonat frequency?

Sol: Given values for HPF

FL = 1000 Hz, R1 = 10 x 103Ω

C1 = == 15.9nF

For LPF,

FH = 30 x 103 Hz, R2 = 10 x 103Ω

C2 =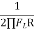==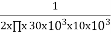 530nF

Central resonat frequency,

Fr =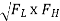

=

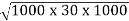
Fr = 5.477 KHz  

Band Stop Filter (BSF) OR Notch FILTER

A notch filter is a Band Stop filter with a narrow band stop bandwidth. These filter are used to attenuate a narrow range of frequencies.

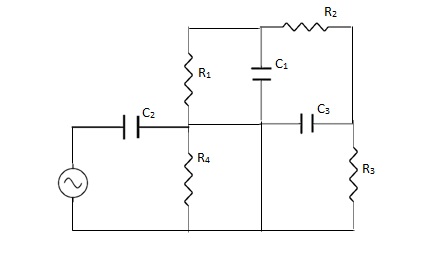
FC = 1 / 2∏RC or  FR =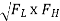

R = 1 / 2∏FCC

Applications of BSF

(i). In telephone technology it is used as noise reducer.

(ii). Widely used in guitar amplifiers.

(iii). For reducing unwanted harmonics.

(iv). Used to reduce static on radio.

(v). In image signal processing.

(vi). Used in biometric instruments like ECG for removing line noise.

Calculation of some basic parameters for T and ∏ section filters

Basic circuit for the calculation of few parameters such as impedance (Zo), and attenuation and phase constants shown below. Here we consider a symmetrical network.

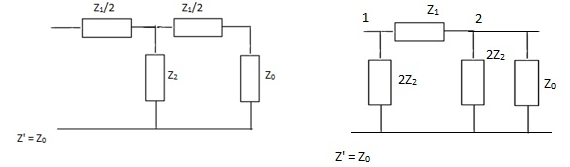
(i). Calculating Zo for T – section fig (a).

Zo =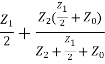

Z0 = +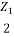

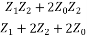
4Z20 + 4Z2Z0 + 2Z1Z0 = Z21 + 4Z1Z2 + 2Z0Z1 + 4Z0Z2

4Z02 = Z12 + 4Z1Z2

Z02 = Z12/4 + Z1Z2

For T-section Z0T =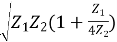         -(1)

(ii). Calculating same for ∏-section network

Zo=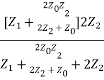

Z0 =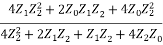

4Z1Z22 = Z02Z1 + 4Z02Z2

Z02 =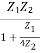

Z0∏ = 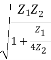     - (2)

From (1) & (2)

Z0T.Z0∏ = Z1Z2

(iii). Attenuation and phase constant for symmetrical T-section shown below.

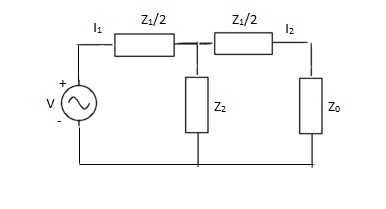
Applying KVL,

V = I1(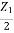+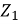) – I2Z2

0 = -I1Z2 + I2(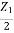 + Z2 + Z0)

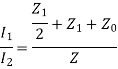
Let 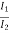= eᵞ

Where ᵞ = Propagation constant

ᵞ = α + jβ

α: attenuation constant(nepers)

β: phase constant(radians)

eᵞ =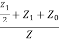

Z0 = Z2(eᵞ - 1)-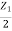

But from eqn (1)

ZOT2 = Z12/4 + Z1Z2

Eliminating Z0 we get

Z2(eᵞ- 1)2 – Z2 eᵞ = 0

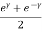= 1 +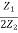

Coshᵞ = 1 +

Since, Sinh=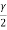

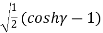
Sinh=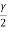

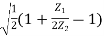
Sinh = 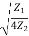- (3)

But ᵞ = α + jβ

Sinh( + )=

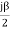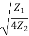
Expanding above equation

Sinh. Cos + jCosh. Sin =

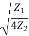
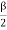When Sinh . Cos = 0

α = 0, β≠ 0. Sin=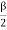

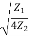
For pass band

α = 0, β = 2Sin-1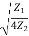|   - (4)

When cos = 0

α≠ 0, β = (2n - 1) ∏

Cosh =

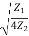
For Stop Band :

α = 2 cos h-1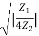, β = ∏    - (5)

7.2 Design of prototype constant k and m derived low pass filter

For such filters the shunt(Z2) and series(Z1) impedances are related as Z1Z2 = K2 = R02

Where k is a constant independent of frequency.

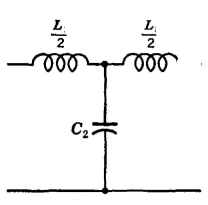
The prototype LPF having symmetrical T and ∏ section is shown below.

(i). Cut off frequency – For both networks

Z1 = jwL, Z2 = 1/jwc

Z1Z2 = L/c = K2 = R02

R0 = √L/C           - (6)

So, cut off frequency is given when,

Z1 = 0 and Z1 + 4Z2 = 0

Jw4 = 0 (Wc = 0)

Z1 + 4Z2 = 0

JWcL + 4/jWcC = 0

Wc = 2/√LC   (WC = 2∏Fc)

Fc = 1/∏√LC         - (7)

(ii). Attenuation constant & Phase Constant

α = 0 ( in pass band )

α = 2Cosh-1√|Z1/4Z2|   - ( in stop band )

Substituting Z1 and Z2

α = 2Cosh-1(F/Fc)   - (8)

β = ∏ ( in stop band )

β = 2Sin-1√|Z1/4Z2|   - ( for pass band )

β = 2Sin-1√F/Fc  - (9)

(iii). Characteristic Impedance for T section and ∏ section

As we already know from equation (1)

ZT = √Z1Z2(1+Z1/4Z2)

Substituting Z1 and Z2

ZOT = √L/C + (1 + jwL/4Ljwc)

= √L/C√1-(F/Fc)2

ZOT = Ro√1-(F/Fc)2   - (10)

From eq (2) we have

ZO∏ = √Z1Z2/1 + Z1/4Z2

Substituting Z1 and Z2 we have

= √4C/1 – w2/LC/4

ZO∏ = Ro/√1-(F/Fc)2    - (11)

m-derived T and ∏ section LPF

F∞ = 1/∏√LC√1-m2 ,  F∞ = FC/√1-m2

FC = 1/∏√LC

m = √1 – (FC/F∞)2

7.3 Design of prototype constant k and m derived high pass filter

Constant K HPF

Basic circuit configuration for constant –k HPF for T section & ∏ section is shown below.

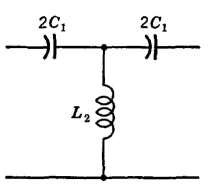
(i). Attenuation & Phase Constant:-

α = 0 ( for pass band )

α = 2Cosh-1√|Z1/4Z2|   - ( for stop band )

α = 2Cosh-1(Fc/F)   - (12)

β = ∏ ( for stop band )

β = 2Sin-1√|Z1/4Z2|   - ( for pass band )

β = 2Sin-1(Fc/F)  - (13)

(ii). Cut off frequency :-

Z1 + 4Z0 = 0, or Z1 = 0

4jWcL + 1/jWcC = 0

Wc = 1/2√LC

Fc = 1/4∏√LC  - (14)

(iii). Calculation of ZOT and ZO∏ -

ZOT = √Z1Z2(1 + Z1/4Z2)

Z1 = 1/jwc, Z2 = jwL

Substituting above Z1 & Z2 and simplifying,

ZOT = RO√1 – (Fc/F)2   -(15)

From equation (2), we have,

ZO∏ =  √Z1Z2/1 + Z1/4Z2

Again substituting Z1, Z2 and simplifying,

ZO∏ = RO/√1 – (Fc/F)2 

Q – Design a constant K LPF T and ∏ section filter having Fc = 1000Hz and nominal characteristic impedance R0 = 400Ω. Also determine the frequency for this filter with attenuation of 19.1 dB.

Sol: FC = 1000 Hz, R0 = 400Ω

FC = 1/∏√Lc, R0 = √L

R0/Fc = √LC/1/∏√LC

R0/Fc =  ∏L

L = 400/∏ x 1000 = 127.32 mH

C = 1/∏FCRo = 1/∏ x 1000 x 400 = 0.795 µF

Attenuation in dB = 8.686 x Attenuation in nepers

Attenuation in nepers = 2.2 nepers

α = 2Cosh-1(F/FC)

F/2 = Cosh(1.1)

F = 3.3 KHz

The design of required filter for T and ∏ section with values L = 127.32 mH. C = 0.795µF is shown below.

m-derived HPF:

F∞ = √1 - m2FC

m = √1 – (F∞/FC)2

FC = 1/4∏√LC

7.4 Design of prototype constant k and m derived band pass filter

Constant K BPF

It is series combination of LPF with an HPF. Which pass a particular band of frequency. The basic structure network of BPF is shown below.

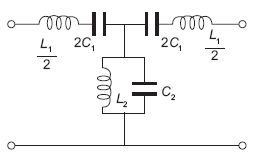
Considering the above circuit, we again calculate few basic parameters related to the circuit.

(i). Ro

In order to allow existence of at least one pass band we assume

Wo2L1C1 = 1 and W02L22C2 = 1

L1C1 = L2C2 = 1/W02      - (16)

Z1 = jwL1 + 1/jWC1 = -W2L1C1 + 1/jWC1

Z2 = jwL2 x 1/jWC2 / jwL2 + 1/jWC2

Z2 = jwL2 / 1 – W2L2C2

But, R02 = Z1Z2

R02 = (jW2L1C1 – 1 / WC1) x (jWL2 / 1 – W2L2C2)

= L2/C1(1 – W2L1C1/1-W2L2C2)

R02 = L2/C1 = Z1Z2

R0 = √L2/C1 = √L1/C2    - (17)

(ii). For cut off frequency we already know

Z1 + 4Z2 = 0

Z1 = -4Z2

Z12 = -4Z1Z2

Z12 = -4R02     ( Since Z1Z2 = R02 )

Z1 = +-j2R0

Z1 = -2jR0    ,    Z2 = +2jR0

( at F = F1 )      ( at F = F2 )

The impedance Z1 is negative of Z2 so,

Z1 = -Z2

j(WL1 – 1/WC1)F=F1 = [ -jWL1 + 1/jWC1 ]F=F2

1 – W12L1C1 = W1/W2(W22L1C1 - 1)

But L1C1 = 1/W02  and W0 = 2∏FC

1 – (F1/F0)2 = F1/F2[ (F2/F0)2 - 1 ]

F2(F02 – F12) = F1(F22 – F02)

F02 = F1F2

F0 = √F1F2    - (18)

(iii). Calculating filter components L1, C1, L2, C2.

As we already know that at F = F1, Z1 = -2jR0.

JW1L1 + 1/jW1C1 = -2jR0

Rearranging and solving above equation,

-(1 – W12L1C1)/W1C1 = -2jR0

1 – (W1/W0)2 = 2R0W1C1(W02 – 1/L1C1)

1 – (F1/F0)2 = 4∏R0F1C1

But F0 = √F1F2

1 – F12/F1F2 = 4∏R0F1C1

C1 = F2 – F1/ 4∏R0F1F2   - (19)

L1C1 = 1/42

L1 = R0/∏(F2 – F1)     - (20)

L1C1 = L2C2 =  1/42

L2/C1 = R02

L2 = R02(F2 – F1)/ 4∏R0F1F2 = R0(F2 – F1)/ 4∏F1F2   - (21)

C2 = L2/R02

C2 = 1/ ∏R0(F2 – F1)    - (22)

Q – Design a constant K BPF with FC = 4KHz and 7KHz and R0 = 500Ω.

Sol: Given:

FC1 = 4000Hz, FC2 = 7000Hz

For BPF,

L1 = R0/ ∏ (F2 – F1) = 500/∏ (7000 – 4000) = 53.05 mH

C1 = F2 – F1/4∏R0F1F2 = 7000 – 4000 / 4∏ x 500 x 7000 x 4000 = 0.017µF

L2 = R0(F2-F1)/ 4∏F1F2 = 500(7000 - 4000) / 4∏ (7000 x 4000) = 42.63 mH

C2 = 1/R0∏ (F2 - F1) = 1/500 x ∏ (7000 - 4000) = 0.212 µF

m-derived BPF:

L1C1 = L2C2 = 1/W02

Infinite attenuation

F∞2 - F∞1 = F2 – F1 / √(1-m2)

m = √1 – (F2 – F1 / F∞2 - F∞1)

7.5 Design of prototype constant k and m derived band stop filter

Constant k- band stop filter

In a constant k band stop filter the components L1, C1 and L2 C2 are chosen such that the shunt resonant frequency of the series arm equals the series resonant frequency of the shunt arm. This frequency is called resonant frequency or the centre frequency f0. Therefore,

i)                   Characteristics Impedance

Wo2L1C1 = 1 and W02L22C2 = 1

L1C1 = L2C2 = 1/W02     

Z1 = (jWL1/ jWC1)/[ jWL1+(1/ jWC1)]= jWL1/1-W2L1C1

Z2 = jWL2+(1/ jWC2) = jW2L2C­2-1/WC2

Since L1C1=L2C2

Z1Z2 = R02

R0 = √L2/C1 = √L1/C2

Ii)                 Cut-off Frequencies

Z1 + 4Z2 = 0

Z1 = -4Z2

Z12 = -4Z1Z2

Z12 = -4R02     ( Since Z1Z2 = R02 )

Z1 = +-j2R0

Z1 = -2jR0    ,    Z2 = +2jR0

The simplification is now done in same way as in case of BPF

F0 = √F1F2   

Iii)              Filter Component Value

The component values at lower cut-off frequencies are given as

L1= (f2-f1)R0/πf1f2

L2=R0/4π(f2-f1)

C1=1/R04π(f2-f1)

C2=(f2-f1)/ πR0 f1f2

m-derived Band stop filter:

Infinite attenuation occurs when

F∞2 - F∞1 = (F2 – F1) √(1-m2)

m = √1 – (F∞2 - F∞1 / F2 – F1)2

Q – Design a constant – k BSF with cut-off frequency of 3KHz and 8KHz and R0 = 600Ω

Sol: F1 = 3000Hz, F2 = 8000Hz, R0 = 600 Ω

L1 = (F2 – F1) R0 / ∏F1F2 = (8000 - 3000) x 600 / ∏ x 8 x 3 x 106 = 5 x 6 x 105 / ∏ x 8 x 3 x 106

L1 = 39.79mH

C1 = 1/4∏R0(F2 – F1) = 1/4∏ x 600(5000) = 0.0265µF

L2 = R0/4∏ (F2 – F1) = 600/4∏ (5000) = 9.54 x 10-3 H

C2 = F2 – F1 / ∏R0F1F2 = 5000 / ∏ x 600 x 8000 x 3000 = 1.105 x 10-3 H

L1/2 = 19.89mH, 2C1 = 0.053 µF

References:

[1] Network Analysis Third Edition by M. E. Van Valkenburg, Prentice Hall of India Private Limited.

[2] Network Analysis & Synthesis by G. K. Mittal, Khanna Publication.

[3] Network Analysis and Synthesis by Ravish R Singh, McGraw Hill.

[4] Introduction to Electric Circuits by Alexander & Sadiku, McGraw Hill.

[5] Introduction to Electric Circuits by S. Charkarboorty, Dhanpat Rai & Co.

[6] Fundamentals of Electrical Networks by B.R.Gupta & Vandana Singhal- S.Chand Publications

[7] Electrical Circuit Analysis 2nd Edition by P. Ramesh babu, Scitech Publication

India Pvt Ltd.