Unit - 6
Hurwitz Polynomial
Hurwitz – A Hurwitz polynomial has all its roots in the either left half plane or simple on imaginary axis conditions to be a Hurwitz polynomial.
(i) All its coefficients are real and positive.
(ii) Both its even and odd powers have roots on imaginary axis.
(iii) The continued fraction expansion of its odd to even or even to odd parts given positive coefficients.
(iv) If F(S) is equal to F1(S) and F2(S) then F(S) will be Hurwitz if both F1(S) and F2(S) are Hurwitz.
(v) The continued expansion of F(S) / F1(S) if gives a positive quotient then polynomial F(S) is Hurwitz.
Q - For the given polynomials find whether they are Hurwitz polynomials or not.
a). F1(S) = S + 3
b). F2(S) = S2 + 5
c). F3(S) = s2 + 5S + 6
d). F4(S) = S3 + 4S2 + 8S + 4
Sol:
a). F1(S) = S + 3
S = -3
Its Hurwitz polynomial
b). F2(S) = S2 + 5
S = Ij√5
Its Hurwitz polynomial
c). F3(S) = S2 + 5S + 6
S2 + 5S + 6
S2 + 2S + 3S + 2 x 3
(S + 3)(S + 2)
F3(S) => S = -3, -2
It is Hurwitz polynomial.
d). F4(S) = S3 + 4S2 + 8S + 4
E(S) = 4S2 + 4 O(S) = S3 + 8S
4(s2 + 1 ) S(S2 + 8)
S = Ij S = Ij2√2
Its Hurwitz polynomial
Q – Find the range of K for which the polynomial 2S4 + S3 + KS2 + S + 2 is Hurwitz?
Sol:

K > 2, K > 4
K > 4
Positive Real Function: A function is said to be positive Real if it has all the poles and zeros on the left half of S-plane and if the function has poles on imaginary axis then it should be simple.
Functions possessing the following properties are called positive real functions, and are abbreviated as prf.
1. When s is real, Z(s) and Y(s) are real functions because the quotients of the polynomials P(s) and Q(s), that is, ak and bk are real. When Z(s) is determined from the impedances of the individual branches, the quotients ak and bk are obtained by adding together, multiplying or dividing the branch parameters which are real.
2. The poles are zeros of Z(s) and Y(s) all lie in the left half of the s-plane, or on the imaginary axis of the s-plane. In the latter case, the poles and zeros are simple. From the above property it should be noted that if the roots of the characteristic equation were lying on the imaginary axis, and the roots s 5 ± jv, were multiples, the solution of the characteristic equation would be of the form
xt = (c0+c1t+c2t2+……cm-1tm-1) sinω1t
This would cause the transients to build up, which cannot happen in a passive one-port. Under these conditions, all quotients an and bn of the polynomials P(s) and Q(s) must be positive. This can be proved by writing the polynomial P(s) as
P(s)= a0sn+a1sn-1+…..+an=a0(s-s1)(s-s2)….(s-sn)
For each pair of complex and conjugate roots, sk=+j ωk and sk+1=+j ωk
3. The real parts of the driving point functions Z(s) and Y(s) are positive, or zero, that is, Re Z(s) > 0 or Re Y(s) > 0 provided for all Re(s) > 0. Let Z(s) = P(S)/Q(S)
Where P(s) and Q(s) are polynomials in s and have real coefficients. Hence, Z(s) is real, when s is real. Further, P(s) and Q(s), are real when s is real. Since the poles and zeros of a network function Z(s) are real, complex zeros must appear in conjugate pairs.
Real Part of Function:
Re [ H(jw) ] >/ 0 for all ‘w’
If a function F(S) is positive real then 1 / F(S) is also positive real. The highest degree and lowest degree of numerator and denominator of function may differ at the most by one. Sum of two positive real function is also positive real.
Q – Find whether the given function F(S) = S + 4 / S2 + 2S + S is positive real or not?
Sol: By inspection check the function
(ii) Numerator and Denominator should both be Hurwitz
(iii) Real part of function must be positive for all values of W.
N(S) = S + 4 D(S) = S2 + 2S + S
It is Hurwitz It is Hurwitz
Finding real part of function, S = jw.
F(jw) = jw + 4 / -w2 + 2jw + 5
= 4 / -w2 + 2jw + 5 + jw / -w2 + 2jw + 5
= 4 + jw/ -w2 + 2jw + 5 x ( -w2 + 5 - 2jw ) / ( -w2 + 5 - 2jw )
= -4w2 + 20 + 2w2 / (-w2 + 5)2 – (2jw)2
Real part
= 20 – 2w2 / w4 + 4w2 – 102 + 25
= 20 – 2w2 / w4 – 6w2 + 25
For, w1 = 1, 2, …
For w > 3 function becomes negative. So not positive real.
Q – 8S6 + 4S5 + 34S4 + 16S3 + 32S2 + 12S + 6. Find whether this is Hurwitz or not?
Sol:

This is the case of premature termination.
F(S) = F1(S).F2(S)
From above F1(S) = 2S4 + 8S2 + 6

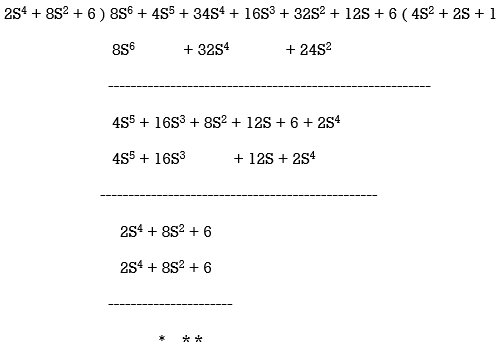
F1(S) = 2S4 + 8S2 + 6 – It is Hurwitz
F2(S) = 4S2 + 2S + 1 – Has one root or RHS
F(S) is not Hurwitz as F2(S) is non Hurwitz.
Properties of the Reactance Function (LC):
(i) All poles and zeros are simple and lies on imaginary axis only.
(ii) It has a pole or zero at infinity and origin.
(iii) It is the quotient of even to odd or odd to even polynomials.
(iv) The residues at all poles are resl and positive.
(v) The slope dF(S) / dw is always positive.
CAUER REALIZATION
If the order of numerator is higher than denominator we perform continuous fraction. If the function is Z(S) the first quotient will be the impedance function, second will be the admittance function an so on. The first element will be the series element.
If the order of the denominator is higher than order of numerator than invert the function. If the function is Y(S) the first element will be the shunt element. The first quotient will be the admittance function. The second will be the impedance and so on.
Cauer Form I
The final structure of this form will be a ladder network whose series arms are inductors and shunt arms are the capacitors.

Since we always have to remove pole at s= ∞ by inverting the remainder and dividing, we can synthesize an LC ladder network by a continued fraction expansion.
Z(s) = Z1(s)+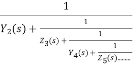
If the Z(s) function being expanded has no poles at infinity then it has a zero there. In such a situation, the function is first inverted and then we proceed as usual. Thus, the nature of first element of the network if fixed by the nature of Z(s) at s= ∞. If Z(s) has a pole at s=∞ the first element is inductor.
Cauer Form II
As we already know that the degree of numerator and denominator must differ by 1 which means that there must be a zero or a pole at the origin. When numerator and denominator of the function are arranged in ascending order we have
Z(s) = ao+a2s2+…..ansn/b1s+b3s3+…..+bmsm
The continued fraction expansion will now become
Z(s) = 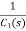 +
+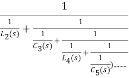
The first term of expansion is impedance the second will be admittance and so on. The resulting network will have capacitor in series and inductors in shunt.
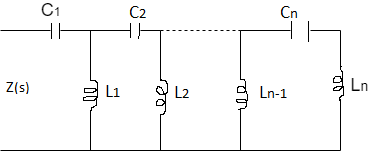
Examples
Q – For the given function Z(S) = 6S3 + 2S / 9S4 + 4S2 + 1 / 6 realise the network function using Cauer foster.
Sol: Degree of denominator is greater so
Y(S) = 9S4 + 4S2 + 1 / 6 / 6S3 + 2S

Y1(S) = 9 / 6S = CS => C = 9 / 6 = 3 / 2
Z2(S) = 6S => L = 6
1 / 3(S) = S => C = 1
Z4(S) = 6S => L = 6
LC Impedance (foster I)
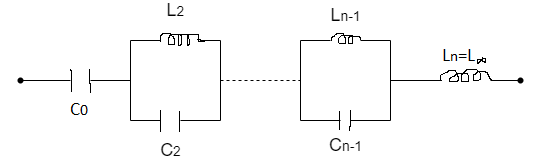
The network consists of a capacitor and then parallel LC network and an inductor as shown above.
Z(S) = K0 / S + 2K1S / S2 + W12 + 2K2S / S2 + W22 + --- + K∞S
K0 = 1 / C0, W12 = 1 / L1C1
C1 = 1 / 2K1, K∞ = L∞
L1 = 2K1 / W12
K0 = SZ(S) | S->0
K1 = Z(S)(S+ Ϭ1) | S = - Ϭ1
K2 = Z(S)(S+ Ϭ2) | S = - Ϭ2
LC Admittance Foster form (2)
The function F(s) is an admittance Y(s) and the partial fraction of it is given as a network consisting of parallel branches shown below.
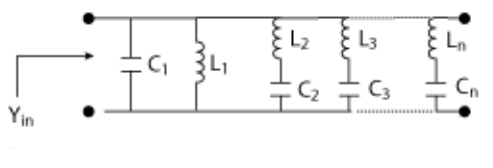
Y(S) = K0/S + 2K1S/S2 + W12 + 2K2S/S2 + W22 + ---- + K∞S
L0 = 1/K0, C∞ = K∞, L1 = 1/2K1, W12 = 1/L1C1
C1 = 2K1 / W12
Properties of RC Impedance [ RL Admittance]:
(i) The poles and zeros are non-respective and lines on negative real axis.
(ii) The poles and zeros are alternate on real axis.
(iii) The lowest critical frequency is a pole.
(iv) The highest critical frequency is a zero.
(v) The residue at all its poles are real and positive
(vi) Z(0) >Z(∞)
w=0 w=∞
Properties of RL Impedance (RC Admittance)
(i) The poles and zeros are simple lies on negative real axis.
(ii) The poles and zeros are alternate on real axis.
(iii) Lowest critical frequency is zero.
(iv) Highest critical frequency is pole.
(v) Z(∞) >Z(0)
Foster Realization
Foster (1) for
(a) RL Impedance: Lowest critical frequency is zero.
Z(S) = K0 + K1S / S + Ϭ1 + k2S / S + Ϭ2 + --------K∞S
R0 = K0, L∞ = K∞, R1 = K1, L1 = K1 / Ϭ1
Ϭ1 = K1 / L1 = R1 / L1
K0 = Z(S) |S -> 0
K1 = Z(S)(S + Ϭ1) / S |S->1
K∞ = Z(S) / S |S -> ∞
(b) RC Impedance (RL Admittance)
The lowest critical frequency is a pole.
Z(S) = K0 / S + K1 / S + Ϭ1 + k2 / S + Ϭ2 + --------K∞
K0 = 1 / C0, R∞ = K∞, K1 = 1 / C1, R1 = K1
Ϭ1 = R1 / K1
K0 = SZ(S) |S->0
K1 = Z(S)(S + Ϭ1) | S = - Ϭ1
K∞ = Z(S)|S->∞
Q – For the function Z(S) = S2 + 6S + 8 / S2 + 4S + 3 is RL or RC.
Realise the above function.
Sol:
Z(S) = S2 + 6S + 8 / S2 + 4S + 3 = (S+4)(S+2) / (S+1)(S+3)
All roots are -4, -2, (-1)->lowest, -3
Since lowest root is pole so its RC.
Ϭ1 = 1, Ϭ2 = 3
Z(S) = K0 / S + K1 / S + Ϭ1 + K2 / S + Ϭ2
K0 = S(S+4)(S+2) / (S+1)(S+3) |S->0 = 0
K∞ = (1 + 6/S + 8/S2 / 1 + 4/S + 3/S2 )S->∞
K∞ = 1 => R∞ =1
K1 = 3/2 => R1 = 2/3 => C1 = 2/3
K2 = (S+4)(S+2) / (S+1)(S+3)(S+3) |S = -3
K2 = 1 / 2 => C2 = 2, R2 = 1/2
Foster form II
(a) RL – admittance:
Y(S) = K0 / S + K1 / S + Ϭ 1 + K2 / S + Ϭ 2 --- K∞
K0 = SY(S) |S->0
K1 = Y(S)( S + Ϭ1) |S = -Ϭ 1
K∞ = Y(S)|S -> ∞
L0 = 1 / K0, R∞ = 1 / K∞, Ϭ1 = R1 / L1
L1 = 1 / K1, Ϭ1 = 1 / R1K1
Q – Realise using foster form (2), Y(S) = S2 + 6S + 8 / S2 + 4S + 3
Sol: Above function is RL admittance as lowest frequency is pole.
Y(S) = (S+4)(S+2) / (S+1)(S+3)
K0 = S(S+4)(S+2) / (S+1)(S+3) |S->0 = 0 , L0 = ∞
K1 = (S+4)(S+2) / (S+1)(S+3)(S+1)|S = -1
K1 = 3 / 2
L1 = 2 / 3, R1 = 2 / 3 (Ϭ1 / K1)
K2 = (S+4)(S+2) / (S+1)(S+3)(S+3) |S = -3
= 1 / 2, L2 = 2, R2 = Ϭ2 / K2 = 3 / ½ = 6
K∞ = (S+4)(S+2) / (S+1)(S+3)|S -> ∞
= (1 + 4 / S)(1 + 2 / S) / (1 + 1 / S)(1 + 3 / S )|S -> ∞
K∞ = 1, R∞ = 1 / K∞ = 1
(b) RC Foster (2) Admittance
Y(S) = K0 + K1S / S + Ϭ 1 + K2S / S + Ϭ 2 + --- +K∞S
K0 = Y(S)|S->0
K∞ = Y(S) / S|S->∞
K1 = Y(S) / S(S + Ϭ1)|S = - Ϭ1
K0 = 1 / R0, C∞ = k∞, K1 = 1 / R1
C1 = K1 / Ϭ1
Q – Realise the following function Y(S) = S2 + 4S + 3 / S2 + 6S + 8
Sol: Lowest critical frequency is zero. Ϭ1 = +4, Ϭ2 = +2
Y(S) = (S+1)(S+3) / S(S+4)(S+2)
K0 = 3 / 8, R0 = 8 / 3
K∞ = (S+1)(S+3) / S(S+4)(S+2)|S->∞
= (1 + 1/S)(1 + 3/S) / S(1 + 4/S)(1 + 2/S)|S->∞
K∞ = 0, C∞ = 0
K1 = (S+1)(S+3)(S+4) / S(S+4)(S+2)|S = - 4
K1 = 3/8, R1 = 8/3
C1 = K1/Ϭ1 = 3/8 x ¼ = 3/32
K2 = (S+1)(S+3) / S(S+4)(S+2)|S = -2 = 1/4
K2 = 1/4, R2 = 4
C2 = K2/ Ϭ2 = 1/8
Cauer Realization for RC and RL
Q – Synthesize the given transfer function using Cauer 1 Z(S) = S2 + 4S + 3 / S2 + 2S?
Sol:

Q – For the function Z(S) = S2 + 4S + 3 / S2 + 2S synthesize using cauer-II?
Sol: Arrange numerator and denominator in ascending order.
Z(S) = 3 + 4S + S2 / 2S + S2
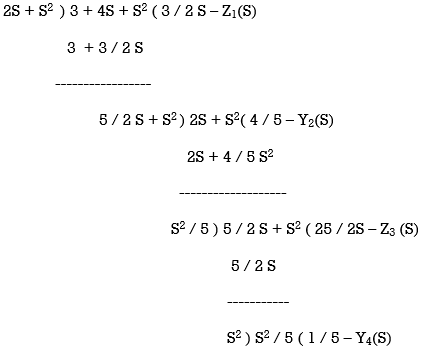
Z1(S) = 3 / 2S = 1 / CS ; C = 2 / 3
Y2(S) – 4 / 5 = 1 / Q ; R = 5 / 4
Z3(S) = 25 / 2S ; C = 2 / 25
Y4(S) = 1 / 5 ; R = 5
Q) The driving point impedance of a one-port reactive network is given by
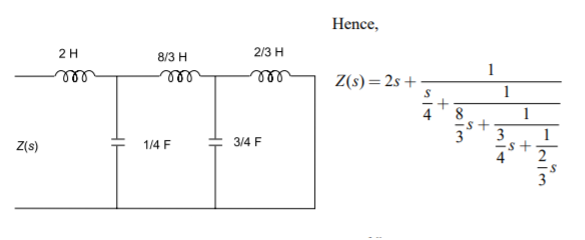
Z(s)= 2s5+12s3+16s/s4+4s2+3. Determine first cauer form of the network?
A) By taking continued fraction expansion, we get
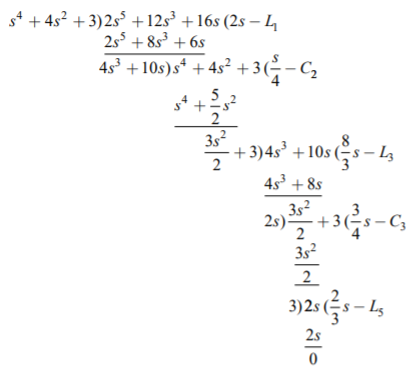
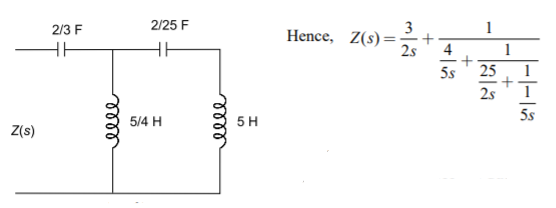
Q) The driving point impedance of an LC network is given by Z(s)= s4 +4s2+ 3/(s3+2s) Determine the second Cauer form of the network.
A) To obtain the second Cauer form, we have to arrange the numerator and the denominator of given Z(s) in ascending powers of s before starting the continued fraction expansion. By taking continued fraction expansion, we get

Q) For the given function find cauer form I, Z(s)=(s+4) (s+8)/(s+2) (s+6)?
A) To find out the first Cauer form, let us take the continued fraction expansion of Z(s)
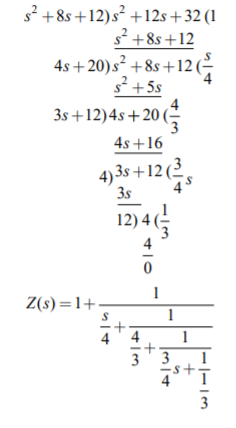
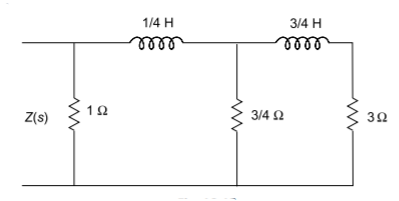
Q) For the transfer function Z(s) = 2s2+8s+16/s2+8s+12. Realise with cauer form II?
A) To find out the second Cauer network, we have to write the impedance function in ascending powers. By taking the continued fraction expansion of Z(s), we have
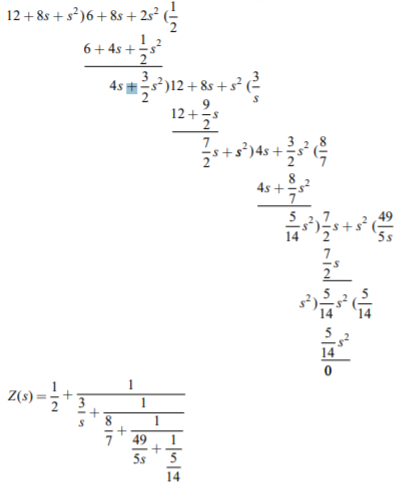
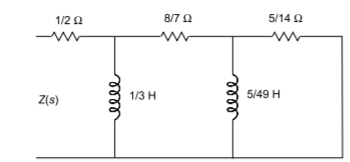
Q) Consider a function Z(s) = (s+2)(s+4)/s(s+3). Find the first cauer form for network?
A) To find the first Cauer form, we take the continued fraction expansion by the divide, invert, divide procedure as follows.

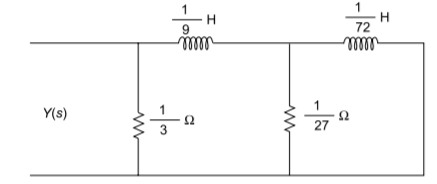
Q) Obtain second cauer form for the function Z(s) = (s+2) (s+4)/s(s+3).
A) The second Cauer network can be obtained by arranging the numerator and denominator polynomials of Z(s) in ascending powers of s. The continued fraction expansion is
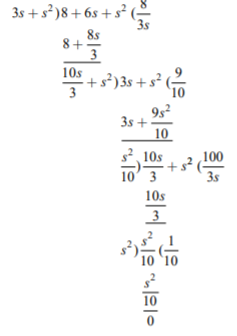

Additional Solved Examples
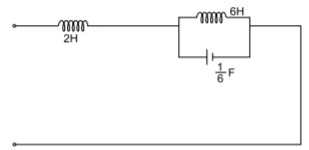
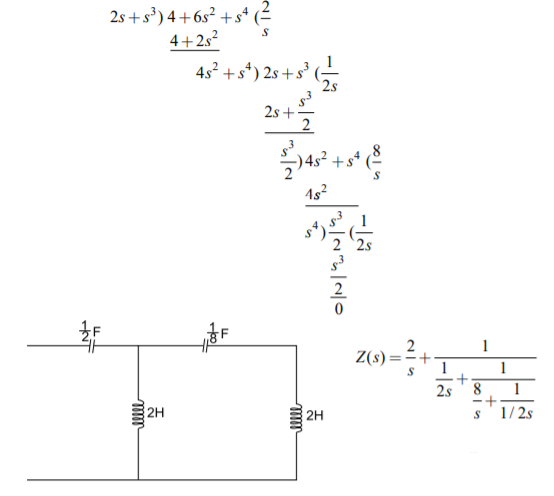
Q) Find the two Foster realisations of the given function. Z(s) = 2s3+8s/s2+1?
A) For the first Foster network, we expand Z(s) into partial fractions
Z(s)= 2s+[6s/s2+1)]
Z(s)= 2s+[3/s+j] +[3/s-j]
L2=6
C2=1/6
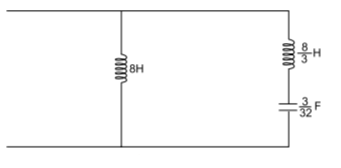
Second Foster network can be obtained by taking admittance function
Y(s)= s2+1/2s(s+4)
Solving by partial fraction we finally have
Y(s)= [1/8s]+[3/16(s+2j)]+[ 3/16(s-2j)]
L0=8H
L1=8/3H
C1=3/32F
The second Foster network with elemental values is shown
Q) Find the two Foster realisations of the given function. Z(s)=3(s2+1) (s2+16)/s(s2+9).
A) For the First Foster network, we expand Z(s) into partial fractions
Z(s)=3s+[24(s2+2)/s(s2+9)]
By partial fraction we have
Z(s)= 3s+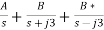
On solving we get
A=16/3
B=28/3=B*
Z(s)= 3s+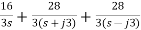
Then the values will be
C0= 1/A=3/16F
C2=1/2B=3/56F
L2=2B/wn2 = 56/27
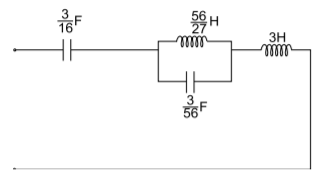
This is the Foster Form I
The Second form of Foster will be
Y(s)= s(s2+9)/s(s2+1) (s2+16)
Solving by partial fraction method
Y(s)= 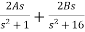
L1=1/2A=90/16H
C1=2A/ wn2 =8/45 F
L2=1/2B=90/14H
C2=2B/ w12=7/720F
The second Foster network with elemental values is shown in Fig.
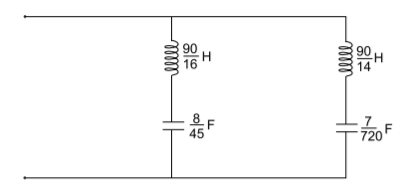
Q) Find the second cauer network of the given function. Z(s)= s4+6s2+4/s3+2s?
A) The second cauer network can be realised by arranging the numerator and denominator polynomials of Z(s) in ascending power of s and taking continued fraction expansion, we get
Q) Find the first and second Cauer forms of the function. Z(s)=2s2+8s+6/s2+2s
A) The first cauer network can be realised by taking continued fraction expansion
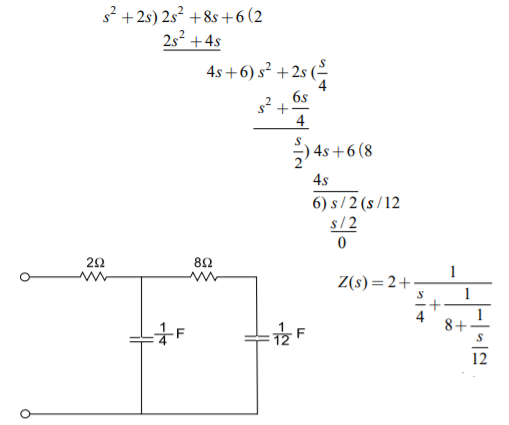
The second Cauer network can be realised by arranging the numerator and denominator polynomials of Z(s) in ascending power of s and taking continued fraction expansion, we get

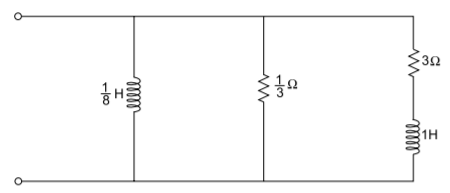
Q) Find the second Foster form and the first Cauer form of the network whose driving point admittance is Y(s)=3(s+2) (s+5)/s(s+3)
A) Taking partial fraction
Y(s)= 3+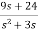 = 3+
= 3+ 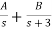
Solving for A and B we get
Y(s)= 3+
The elemental values will be
R=1/3
L=1/8H
R1=3 
L1=1H
Therefore, the second Foster network is shown in Fig.
To get the first cauer realisation, we take continued fraction expansion from the expression.
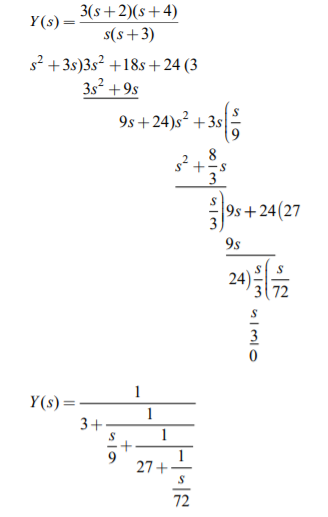
Therefore, the admittance, Y(s), can be realised as RL network shown in Fig.
Q) Find the two Foster realisation of Z(s) =4(s2+1)(s2+16)/s(s2+4)?
A) For the first Foster network, we expand Z(s) into partial fractions
Z(s)= 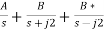
Solving for A and B we get
A= 16
B=18
C0= 1/A=1/16F
L∞ =4H
C2=1/2B=1/36F
L2=2B/wn2 = 9H
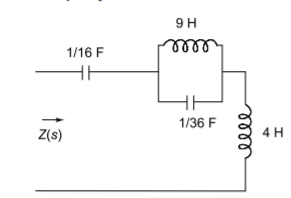
For second form of foster we take admittance function
Y(s)=s(s2+4)/ 4(s2+1)(s2+16)
Solving by partial fraction we get
Y(s)= 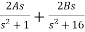
A=1/40
B=1/10
The elements value will be
L1=1/2A=20H
C1=2A/w12=1/20F
L2=1/2B=5H
C2=2B/w12=1/80F

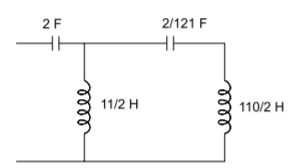
Q) Find the two Cauer realisations of driving point function given by Z(s)= 12s4+12s2+1/2s3+2s
A) By taking the continued fraction expansion, we get
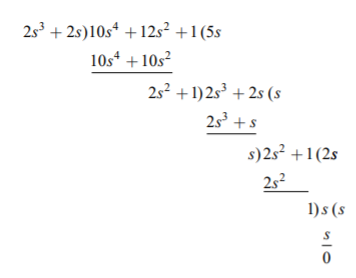

To realise the second Cauer network, we have to take ascending powers of impedance function.
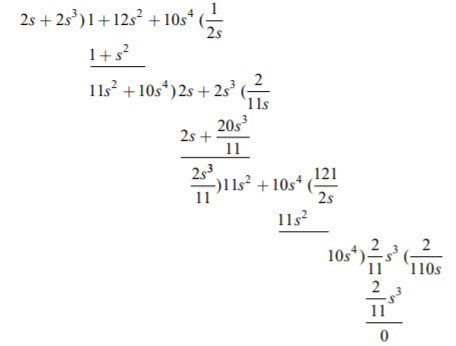

References:
- [R1] William H. Hayt, Jr. Jack E. Kemmerly, “Engineering Circuit Analysis” McGraw Hill Publication.
- [R2] N.C. Jagan, “Network Analysis”, BS Publication, Hyderabad, Second Edition.
- [R3] G. K. Mittal, “Network Analysis and Synthesis”, Khanna Publication.