Unit - 5
Graphs and Trees
Basic terminology-
Graph theory is a relatively new area of mathematics
Graph is the form of representing of descriptive data in the terms of verticals and edges.
Graph theory is used in various fields like computer science, information technology, genetics, telecommunication etc.
A graph is a collection of vertices and edges in which each edge is assigned to pair of points called terminal.
We can say that a graph is a network of dots connected by lines.
Mathematically we can define a graph as-
A graph is a pair of set (V, E) where-
1. V is a non-empty set whose elements are called vertices.
2. E is collection of two-element subset of V called edges.
Terminology: A graph G is an ordered pair (V, E) where V is a non-empty set and E is the set of edges in which each element of E is assigned to a unique unordered pair of elements of V.
An element of a set E is generally denoted as- e = (v,u) where u, v ∈ V.
U and v are called the end vertices of edge e.
Note- In any graph the number of vertices with odd degree must be even.
Loop: If both the end vertices of an edge are same then the edge is called a loop.
Parallel edge: If two or more edges have same terminal vertices, then these edges are called parallel edges.
Example: Consider the graphs given below-
G1 = {V1, E1}, where V1 = {a, b, c} and E1 = {{a, b},{a, c}, {b, c}},
G2 = {V2, E2}, where V2 = {u, v, w} and E1 = {{u,v,},{u,w},{v,w}}
Check whether these graphs are same or not?
Sol.
As we can see that these graphs are not same because here V1 and V2 are not same since a ∈ V1 but a does not belongs to V2.
These two graphs look same but not equal.
We can draw these graphs as below-
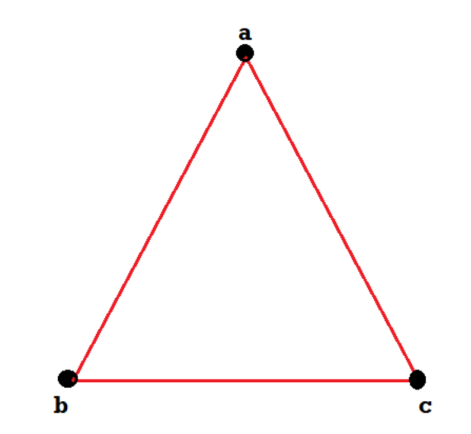
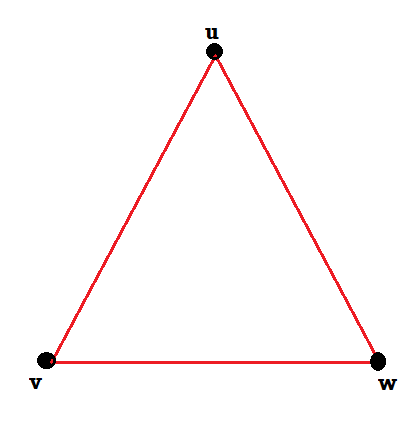
These types of graphs are known as isomorphic graph when they are same except for the name of vertices.
Simple graph: A graph which has no loops and parallel edges is known as simple graph.
Compound graph: A graph which contains loops or parallel edges is called compound or multi-graph.
Degree of vertex: The number of edges incident on a vertex v is called degree of vertex v, with loop being counted twice.
We can denote it as-
Degree of v = d(v)
Examples of graph and multi-graph are-
Graph-
Multi-graph-
Weighted Graphs
A graph G is said to be a weighted graph if each edge e of G is assigned a non-negative number w(e) called the weight of v.
The weighted graph is given below-
Sub Graphs-
We can say that G' = (V', E') is a sub-graph of G = (V, E), and write G' ⊆ G provided V' ⊆ V and E' ⊆ E.
We can say that G' = (V', E') is an induced sub-graph of G = (V, E), provided V' ⊆ V and every edge in E whose vertices are still in V' is also an edge in E'.
Isomorphic graphs-
Let G1(V1, E1) and G2(V2, E2) be two graphs. The graph G1 and G2 are said to be isomorphic if there is a bijective function fv : V1 → E1 such that if u and v are end vertices of some edge e ∈ E1 then fv(u), fv(v) end vertices of fE(e).
Complete Graphs-
A simple graph G is called a complete graph, if there is an edge between each pair of vertices.
Regular Graphs-
If all vertices of a graph G have same degree, then G is called as a regular graph.
Bipartite Graphs-
A graph G(V, E) is said to be bipartite, if the vertex set V can be partitioned in to two non-empty disjoint subset V1 and V2 such that each edge is G had end vertex is V1 and other end vertex in V2 .
There is no edge between two vertices of V1 as well as there is no edge between two vertices of V2.
Here V1V2 bipartition of V.
Trees-
A graph T is called a tree if T is connected and T has no cycles.
A graph without cycle is said to be a cycle-free.
The tree consisting of a single vertex with no edges is called the degenerated tree.
One thing to keep in mind is that while the trees we study in graph theory are related to trees you might see in other subjects, the correspondence is not exact. For instance, in anthropology, you might study family trees, like the one below
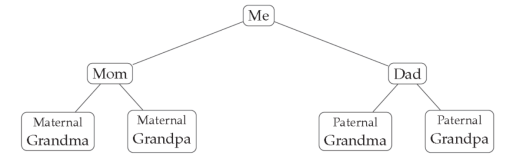
So far so good, but while your grandparents are (probably) not blood relatives, if we go back far enough, it is likely that they did have some common ancestor. If you trace the tree back from you to that common ancestor, then down through your other grandparent, you would have a cycle, and thus the graph would not be a tree.
You might also have seen something called a decision tree (such as the algorithm for deciding whether a series converges or diverges). Sometimes these too contain cycles, as the decision for one node might lead you back to a previous step.
Both the examples of trees above also have another feature worth mentioning: there is a clear order to the vertices in the tree. In general, there is no reason for a tree to have this added structure, although we can impose such a structure by considering rooted trees, where we simply designate one vertex as the root.
Spanning trees-
A sub-graph T of a connected graph G is called spanning tree of G if T is a tree and T includes all the vertices of G.
Rooted trees-
As soon as one vertex of a tree is designated as the root, then every other vertex on the tree can be characterized by its position relative to the root. This works because there is a unique path between any two vertices in a tree. So from any vertex, we can travel back to the root in exactly one way. This also allows us to describe how distinct vertices in a rooted tree are related.
If two vertices are adjacent, then we say one of them is the parent of the other, which is called the child of the parent. Of the two, the parent is the vertex that is closer to the root. Thus the root of a tree is a parent, but is not the child of any vertex (and is unique in this respect: all non-root vertices have exactly one parent).
Not surprisingly, the child of a child of a vertex is called the grandchild of the vertex (and it is the grandparent). More in general, we say that avertexv is a descendent of a vertex u provided u is a vertex on the pathfromv to the root. Then we would call u an ancestor of v.
For most trees (in fact, all except paths with one end the root), there will be pairs of vertices neither of which is a descendant of the other. We might call these cousins or siblings. In fact, vertices u and v are called siblings provided they have the same parent. Note that siblings are never adjacent
Example- consider the tree below-
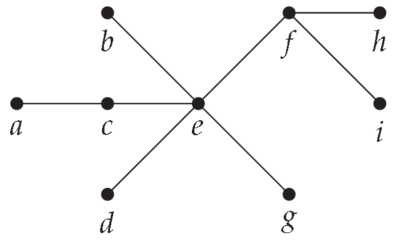
If we designate vertex f as the root, then e, h, and i are the children of f, and are siblings of each other. Among the other things we can say are that a is a child of c, and a descendant of f. The vertex g is a descendant of f , in fact, is a grandchild of f . Vertices g and d are siblings, since they have the common parent e.
Notice how this changes if we pick a different vertex for the root. If a is the root, then its lone child is c, which also has only one child, namely e. We would then have f the child of e (instead of the other way around), and f is the descendant of a, instead of the ancestor. f and g are now siblings.
Example-
Explain why every tree is a bipartite graph.
Solution.
To show that a graph is bipartite, we must divide the vertices into two sets A and B so that no two vertices in the same set are adjacent. Here is an algorithm that does just this.
Designate any vertex as the root. Put this vertex in set A. Now put all of the children of the root in set B. None of these children are adjacent (they are siblings), so we are good so far. Now put into A every child of every vertex in B (i.e., every grandchild of the root). Keep going until all vertices have been assigned one of the sets, alternating between A and B every “generation.” That is, a vertex is in set B if and only if it is the child of a vertex in set A.
Spanning trees-
Given a connected graph G, a spanning treeof G is a sub-graph of G which is a tree and includes all the vertices of G.
Every connected graph has a spanning tree.
Example: Find two different spanning tree of the graph.
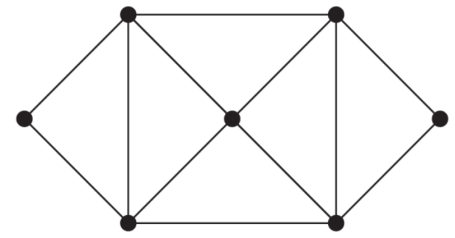
Sol-
Two spanning trees are-
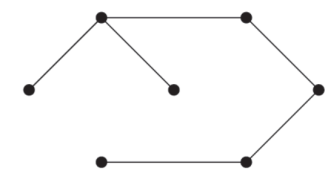
And
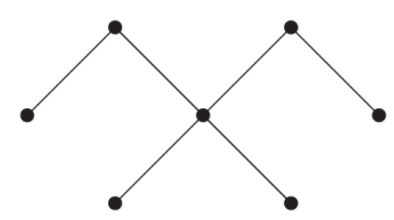
Isomorphism
Two graphs are said to be isomorphic if there exist one to one correspondence from I to V.
1. They must have same no. Of vertices.
2. They must have same no. Of edges.
3. They must have same degree of vertices.
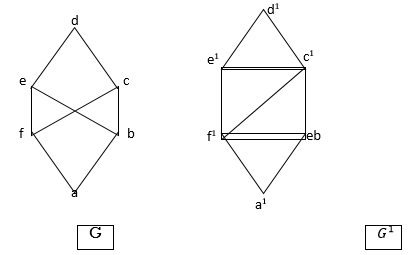
Q. Are the following pairs of graphs isomers?
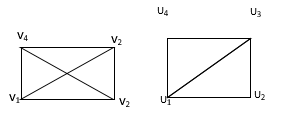
Yes, G1 & G2 both have 4 vertices, 5 edges
2 vertices of degree 2.
2 vertices of degree 3.
V1 U1 V3 U2
V2 U3 V4 U4
Q. Determine whether are isomorphic
i) The same no. Of vertices viz. 6
Ii) But they do not have same number of edges, G has 8 edges, “G” has 7 edges.
Iii) In “G” the vertex “C” is of degree 44.
In G there is no vertex of degree 4.
G &G1 are not isomorphic.
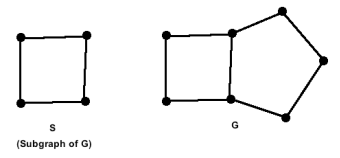
Subgraph
A subgraph S of a graph G is a graph whose set of vertices and set of edges are all subsets of G. (Since every set is a subset of itself, every graph is a subgraph of itself.)
All the edges and vertices of G might not be present in S; but if a vertex is present in S, it has a corresponding vertex in G and any edge that connects two vertices in S will also connect the corresponding vertices in G.
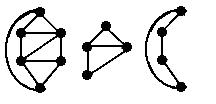
All of these graphs are subgraphs of the first graph.
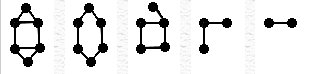
A vertex-induced subgraph is one that consists of some of the vertices of the original graph and all of the edges that connect them in the original. An edge-induced subgraph consists of some of the edges of the original graph and the vertices that are at their endpoints.
 | The second two figures are vertex-induced subgraphs of the first figure. |
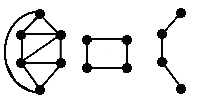 | The second two figures are edge-induced subgraphs of the first figure. |
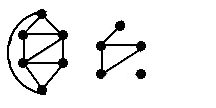 | The second figure is a subgraph of the first figure, but it is neither edge-induced nor vertex-induced. |
A spanning subgraph is a subgraph that contains all the vertices of the original graph. A spanning tree is a spanning subgraph that is often of interest. A cycle in a graph that contains all the vertices of the graph would be called a spanning cycle. However it's more common name is a Hamiltonian cycle.
Example: Graph S is a subgraph of G:
1. Rooted Trees
A rooted tree is a tree in which one vertex has been designated as the root and every edge is directedaway from the root.
2. Parent
Suppose that T is a rooted tree. If v is a vertex in T other than the root, the parent of v is the unique vertex u such that there is a directed edge from u to v.
3. Child
If u is the parent of v, then v is called a child of u.
4. Siblings
Vertices with the same parent are called siblings.
5. Ancestors
The ancestors of a vertex other than the root are the vertices in the path from the root to this vertex, excluding the vertex itself and including the root.
6. Descendants
The descendants of a vertex v are those vertices that have v as an ancestor.
7. Leaf
A vertex of a tree is called a leaf if it has no children.
8. Internal Vertices
Vertices that have children are called internal vertices.
9. Sub tree
If a is a vertex in a tree, the sub tree with a as its root is the sub graph of the tree consisting of a and its descendants and all edges incident to these descendants.
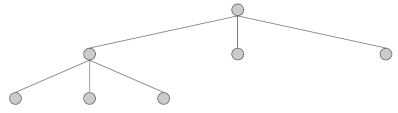
10. M-ary Tree
A rooted tree is called an m-ary tree if every internal vertex has no more than m children. The tree is called a full m-ary tree if every internal vertex has exactly m children.
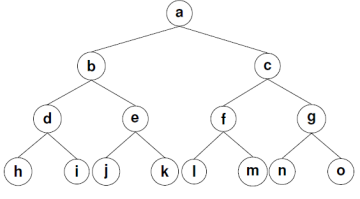
11. Example of a full 3-ary tree:
The tree which includes all the vertices of the connected undirected graph G very minimally is known as a spanning tree. A single graph can have many spanning trees.
Example:
After spanning the above graph becomes
An m-ary tree with m = 2 is called a binary tree.
Ordered Root Tree
An ordered rooted tree is a rooted tree where the children of each internal vertex are ordered.
Left and Right Child
In an ordered binary tree, the first child is called the left child and the second child is called the Rightchild.
Left and Right Sub tree
The tree rooted at the left child is called the left sub treeand the tree rooted at the right child is called the right sub tree.
Example 1: Every binary tree has an odd no of vertices.
Solution: let T = (V, E) be a binary tree.
A part from the root every vertex in a binary tree is an odd degree.
w.k.t., there must be an even no. Of vertices such odd degree.
When the root which of odd degree is added to this even no. Of vertices i.e.,
Even no. Of vertices and one root vertex, we have odd no. Of vertices.
Therefore, every binary tree has odd no. Of vertices
Note: let a tree has ‘n’ vertices and ‘m’ pendent vertices, then the no. Of internal vertices of degree 3 is n-(m+1)
Example 2: prove that there are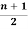 
pendent vertices in any binary tree with ‘n’ vertices.
Solution: suppose T = (V, E) be a binary tree with ‘n’ vertices. Let ‘m’ be the two no. Of pendent vertices in T. Then T has (n-(m+1)) no. Of internal vertices of degree 3
So, the sum of degree of all vertices in T is 3(n-m-1) + m+2….(1)
Since T is tree with ’n’ vertices then it has (n-1) edges.
So, the degree sum of ‘n’ vertices in T is given by
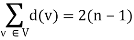
(2)
From (1) and (2)
3(n - m - 1) + m + 2 = 2(n - 1)
→ 3n - 3m - 3 + m + 2 = 2n - 2
→ n - 2m + 1 =0
→ n + 1 = 2m
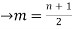
The no. Of pendent vertices in binary tree is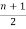 
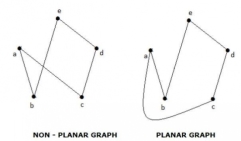
A graph 'G' is said to be planar if it can be drawn on a plane or a sphere so that no two edges cross each other at a non-vertex point.
Euler’s formula for planar graph-
For any planar graph with v vertices, e edges and f faces, we have-
v + f = 2 + e
Example
Regions
Every planar graph divides the plane into connected areas called regions.
Example 1:
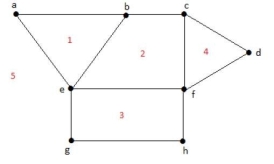
Solution: Degree of a bounded region r = deg(r) = Number of edges enclosing the regions r.
Deg (1) =3
Deg (2) =4
Deg (3) =4
Deg (4) =3
Deg (5) =8
Example 2:
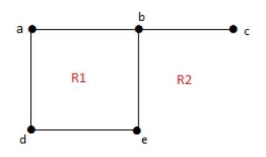
Solution: Degree of an unbounded region r = deg(r) = Number of edges enclosing the regions r.
Deg (R1) = 4
Deg (R2) = 6
In planar graphs, the following properties hold good –
1. In a planar graph with 'n' vertices, sum of degrees of all the vertices is
n ∑ i=1 deg (Vi) = 2|E|
2. According to Sum of Degrees of Regions Theorem, in a planar graph with 'n' regions, Sum of degrees of regions is −
n ∑ i=1 deg(ri) = 2|E|
Based on the above theorem, you can draw the following conclusions −
In a planar graph,
- If degree of each region is K, then the sum of degrees of regions is
K|R| = 2|E|
- If the degree of each region is at least K (≥ K), then
K|R| ≤ 2|E|
- If the degree of each region is at most K (≤ K), then
K|R| ≥ 2|E|
Note− Assume that all the regions have same degree.
3. According to Euler's Formulae on planar graphs,
- If a graph 'G' is a connected planar, then
|V| + |R| = |E| + 2
- If a planar graph with 'K' components then
|V| + |R|=|E| + (K+1)
Where, |V| is the number of vertices, |E| is the number of edges, and |R| is the number of regions.
4. Edge Vertex Inequality
If 'G' is a connected planar graph with degree of each region at least 'K' then,
|E| ≤ 
- 2{|v|-2}
You know, |V| + |R| = |E| + 2
K.|R| ≤ 2|E|
K (|E| - |V| + 2) ≤ 2|E|
(K - 2) |E| ≤ K (|V| - 2)
|E| ≤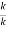 
- 2{|V| - 2}
5. If 'G' is a simple connected planar graph, then
|E| ≤ 3 |V| - 6
|R| ≤ 3 |V| - 4
There exists at least one vertex V∈ G, such that deg(V) ≤ 5
6. If 'G' is a simple connected planar graph (with at least 2 edges) and no triangles, then
|E| ≤ (2|V| - 4)
Key takeaways
- For any planar graph with v vertices, e edges and f faces, we have- v+f = 2+e
- A graph 'G' is said to be planar if it can be drawn on a plane or a sphere so that no two edges cross each other at a non-vertex point.
Euler Path: An Euler’s path contains each edge of ‘G’ exactly once and each vertex of ‘G’ at least once. A connected graph G is said to be traversable if it contains an Euler’s path.
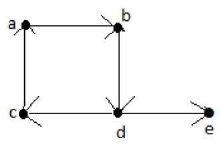
Euler’s Path = d-c-a-b-d-e.
Example 1: Find the Eulerpath for the following figure
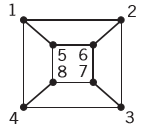
Solution:
The graph G1has an Euler circuit for example a,e,c,d,e,b,a has Euler circuit. Neither of the graphs G2 OR G3 has Euler circuits.G3 has an Euler path but not the circuit.
Example 2: Find the Euler path for the following figure.
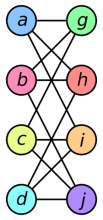
Solution:
The graph H2 has a Euler circuit i.e., a,g,c,b,g,e,d,f .Neither H3 or H1 has the Euler path but namely H3 has Euler path but not the circuit.
Multigraphs
Multigraph is a graph in which numerous edges between the same set of vertices are allowed. To put it another way, it's a graph with at least one loop and numerous edges.
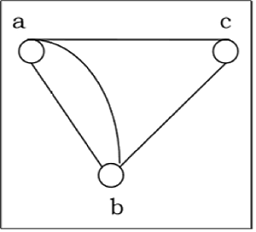
Fig: Multigraph
A Euler Path through a graph is a path whose edge list contains each edge of the graph exactly once.
Euler Circuit: A Euler Circuit is a path through a graph, in which the initial vertex appears a second time as the terminal vertex.
Euler Graph:A Euler Graph is a graph that possesses a Euler Circuit. A Euler Circuit uses every edge exactly once, but vertices may be repeated.
Example - The graph shown in fig is a Euler graph. Determine Euler Circuit for this graph.
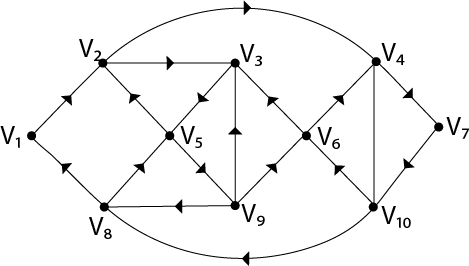
Fig: Euler graph
Solution - The Euler Circuit for this graph is
V1, V2, V3, V5, V2, V4, V7, V10, V6, V3, V9, V6, V4, V10, V8, V5, V9, V8, V1
For a connected network with no vertices of odd degrees, we can create a Euler Circuit.
State and Prove Euler's Theorem:
Consider any linked planar network with R regions, V vertices, and E edges, G= (V, E). V+R-E=2 in this case.
Proof: To prove this theorem, use induction on the number of edges.
Basis of Induction:Assume that each edge has the value e=1.
Then there are two examples, both of which have graphs in fig:
We have V=2 and R=1 in Fig. As a result, 2+1-1=2.
V=1 and R=2 is shown in Fig. As a result, 1+2-1=2.
As a result, the induction's foundation is established.
Induction step: Assume the formula is valid for connected planar graphs with K edges.
Consider the graph G, which has K+1 edges.
To begin, we assume that G is devoid of circuits. Take a vertex v and create a path that starts at v. We have a new vertex whenever we locate an edge in G since it is a circuit-free language. Finally, we'll arrive at a vertex v with degree 1. As a result, we are unable to proceed as depicted in fig.
Remove the corresponding edge incident on v and the vertex v. As a result, we have a graph G* with K edges, as shown in fig.
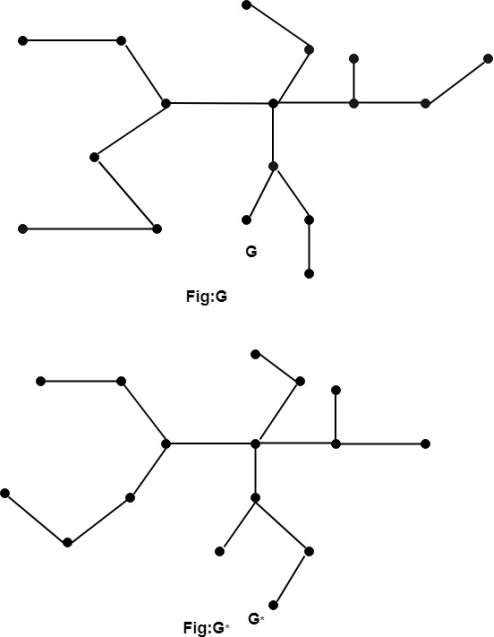
As a result, Euler's formula holds for G* by inductive assumption.
Now, G has one extra edge and one more vertex than G*, with the same number of regions. As a result, the formula also applies to G.
Second, we suppose that G contains a circuit and that e is an edge in the circuit depicted in figure:
Now, because e is a portion of a two-region boundary. As a result, we merely delete the edge, leaving us with a graph G* with K edges.
As a result, Euler's formula holds for G* by inductive assumption.
G now has one more edge than G*, as well as one more area with the same number of vertices as G*. As a result, the formula also holds for G, proving the thesis by verifying the inductive steps.
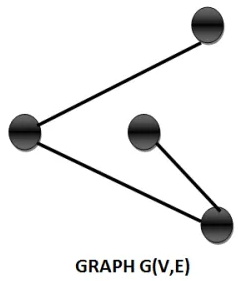
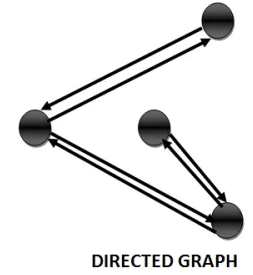
A closed path that visits every vertex in G exactly once and if G admit a Hamiltonian circuit, then G is called Hamiltonian graph.
Note- A Eulerian circuit traverses every edge exactly once, but many repeats’ vertices.
While a Hamiltonian circuit visits each vertex exactly once but many repeats’ edges.
Following are the examples of Hamiltonian and Eulerian graph respectively-
Note:
- Euler’s circuit contains each edge of the graph exactly once.
- In a Hamiltonian cycle, some edges of the graph can be skipped.
Example:
Take a look at the following graph-
For the graph shown above-
- Euler path exists – false
- Euler circuit exists – false
- Hamiltonian cycle exists –true
- Hamiltonian path exists –true
G has four vertices with odd degree, hence it is not traversable. By skipping the internal edges, the graph has a Hamiltonian cycle passing through all the vertices.
Graph colourings:
Consider a graph G. A vertex coloring, or simply a coloring of G is an assignment of colors to the verticesof G such that adjacent vertices have different colors.We say that G is n-colorable if there exists a coloring of Gwhich uses n colors. (Since the word “color” is used as a noun, we will try to avoid its use as a verb by saying, for example, “paint” G rather than “color” G when we are assigning colors to the vertices of G.) The minimumnumber of colors needed to paint G is called the chromatic number of G and is denoted by χ(G).
An algorithm by Welch and Powell for a coloring of a graph G. We emphasize that thisalgorithm does not always yield a minimal coloring of G.
Algorithm (Welch-Powell): The input is a graph G.
Step 1. Order the vertices of G according to decreasing degrees.
Step 2. Assign the first color C1 to the first vertex and then, in sequential order, assign C1 to each vertex which is not adjacent to a previous vertex which was assigned C1.
Step 3. Repeat Step 2 with a second color C2 and the subsequence of noncolored vertices.
Step 4. Repeat Step 3 with a third color C3, then a fourth color C4, and so on until all vertices are colored.
Step 5. Exit
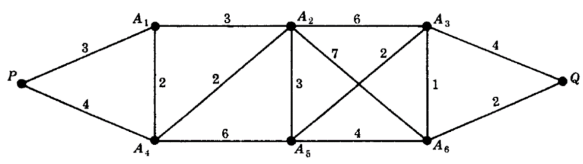
Example: Consider the graph G in Fig. Below. We use the Welch-Powell Algorithm to obtain a coloring ofG. Orderingthe vertices according to decreasing degrees yields the following sequence:
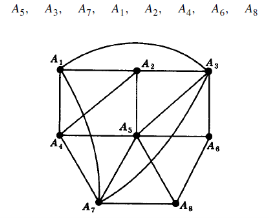
The first color is assigned to vertices A5 and A1. The second color is assigned to vertices A3, A4, and A8.
The third color is assigned to vertices A7, A2, and A6. All the vertices have been assigned a color, and so Gis 3-colorable. Observe that G is not 2-colorable since vertices A1, A2, and A3, which are connected to eachother, must be assigned different colors. Accordingly, χ(G) = 3.
(b) Consider the complete graph Kn with n vertices. Since every vertex is adjacent to every other vertex, Kn requires n colors in any coloring. Thus χ(Kn) = n.
There is no simple way to actually determine whether an arbitrary graph is n-colorable. However, thefollowing theorem gives a simple characterization of 2-colorable graphs.
Theorem: The following are equivalent for a graph G:
(i) G is 2-colorable.
(ii) G is bipartite.
(iii) Every cycle of G has even length.
There is no limit on the number of colors that may be required for a coloring of an arbitrary graph since, forexample, the complete graph Knrequires n colors. However, if we restrict ourselves to planar graphs, regardlessof the number of vertices, five colors suffice.
Four Color Theorem (Appel and Haken):
Any planar graph is 4-colorable.
Four Color Theorem (Appel and Haken): If the regions of any map M are colored so that adjacent regionshave different colors, then no more than four colors are required.
The proof of the above theorem uses computers in an essential way. Specifically, Appel and Haken first showed that if the four color theorem was false, then there must be a counterexample among one of approximately 2000different types of planar graphs. They then showed, using the computer, that none of these types of graphs hassuch a counterexample. The examination of each different type of graph seems to be beyond the grasp of humanbeings without the use of a computer. Thus the proof, unlike most proofs in mathematics, is technology dependent; that is, it depended on the development of high-speed computers.
References:
1. Discrete Mathematics and its Applications, Kenneth H. Rosen, 7th Edition, McGraw HillEducation (India) Private Limited.
2. Discrete Mathematics D.S. Malik & K. K. Sen, Revised Edition Cengage Learning.
3. Elements of Discrete Mathematics, C.L. Liu and D.P. Mohapatra, 4th Edition, McGraw HillEducation (India) Private Limited.
4. Discrete Mathematics with Applications, Thomas Koshy, Elsevier.
