Unit - 4

Recurrence Relations

4.1 Generating Functions of Sequences

For a numeric function-

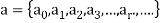
An infinite series is defined as-

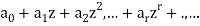which is called the generating function of a.

We denote it by A(Z).

The coefficient of 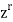is A (z) is the value of the numeric function a.

For example:

If the generating function is

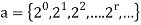
Is

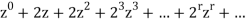
We can write the above series as below-

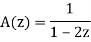
In 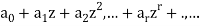  the term 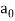is called the constant term.

Let

And

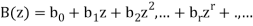
Are the generating functions.

A(z) and B(z) are equal if , for each

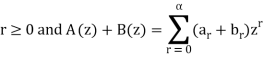
The product can be defined as-

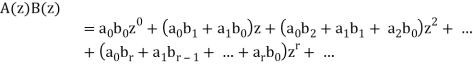
Note-

1. The ordinary generating function is the formal power series-

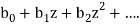
2.     the exponential generating function (egf) is the formal power series

3.     If the sequence has finitely many elements then the generating functions have finitely many terms.

4.2 Calculating Coefficients of Generating Functions

Suppose r and k are non-negative integers. A recurrence relation of the form

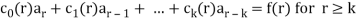
Here and f(r) are the functions of r is said to be a recurrence relation.

If 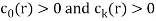then it said to be a linear recurrence relation of degree k..

Linear recurrence relation with constant coefficient-

If 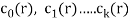are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.

A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form

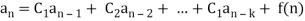
Where 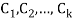are constant with 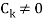and f(n) is a function of ’n’.

Example: Consider a following recurrence relation-

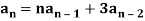
Sol.

It is a homogeneous linear second-order recurrence relation but it does not have constant coefficients because the coefficient of 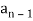is not a constant given initial conditions 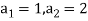, the next elements of the sequence follows-

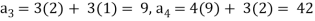
Note-

If iff (r) = 0, then the recurrence relation is called a linear homogenous relation.

For example:

The following relations are linear recurrence relations with constant coefficients-

an - 6an + 11 an-1 + 6an-3 = 2n

an - 9an-1 + 26an-1 - 24 an-3 = 5n

Key takeaways

1. If 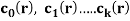are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.
2. A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form

an = C1 an-1 + C2 an-2 + . . . + Ck an-k + f(n)

Where 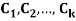are constant with 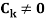and f(n) is a function of ’n’.

4.3 Recurrence relations

Recursion is a technique of defining a function, a set or an algorithm in terms of itself.

Suppose the set of natural numbers, we introduce the method of generating the set of natural numbers by recursion.

The natural numbers with zero are those objects which can be generated by starting with an initial object 0 and from any object “n” already generated passing to another uniquely determined object 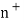, the successor of n. The objects differently generated are always distinct. Thus the natural numbers appear as a set of objects 0,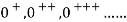

The transition to the usual notation is made upon introducing 1, 2, 3, 4, … to stand for 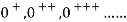and then employing the notation.

The recursive formula for defining a sequence (or numeric function) is called a recurrence relation.

A recurrence relation is also called a difference equation.

The information accompanying a recursive formula about the beginning of the numeric function is called initial condition.

Example: Find a recurrence relation and initial conditions for 1, 5, 17, 53, 161, 485 .

Sol.

Here 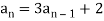is the recurrence relation and the initial condition is

Example: Check whether 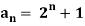is a solution to the recurrence relation 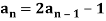with .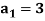

Sol.

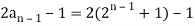
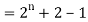
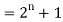
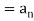
Key takeaways

1. The recursive formula for defining a sequence (or numeric function) is called a recurrence relation.
2. A recurrence relation is also called a difference equation.
3. The information accompanying a recursive formula about the beginning of the numeric function is called initial condition.

Linear recurrence relations with constant coefficients

Suppose r and k are non-negative integers. A recurrence relation of the form

c0(r) ar + c1(r)ar-1 + . . . + ck(r) ar-k = f(r) for r ≥ k

Here 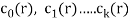and f(r) are the functions of r is said to be a recurrence relation.

If 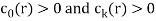then it said to be a linear recurrence relation of degree k..

Linear recurrence relation with constant coefficient-

If 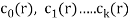are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.

A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form

an = C1 an-1 + C2an-2 + . . . + Ck an-k + f(n)

Where 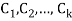are constant with 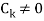and f(n) is a function of ’n’.

Example: Consider a following recurrence relation-

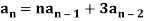
Sol.

It is a homogeneous linear second-order recurrence relation but it does not have constant coefficients because the coefficient of 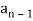is not a constant given initial conditions 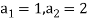, the next elements of the sequence follows-

a3 = 3(2) + 3(1) = 9,   a4 = 4(9) + 3(2) = 42

Note-

If iff (r) = 0, then the recurrence relation is called a linear homogenous relation.

For example:

The following relations are linear recurrence relations with constant coefficients-

an - 6an-1 + 11an-1 + 6an-3 = 2n

an - 9an-1 + 26an-1 - 24 an-3 = 5n

Key takeaways

1. If 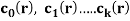are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.
2. A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form

an = C1an-1 + C1an-2 + . . . + Ck an-k + f(n)

Where 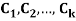are constant with 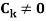and f(n) is a function of ’n’.

Total solutions

The total solution or the general solution of a non-homogeneous linear difference equation with constant coefficients is the sum of the homogeneous solution and a particular solution. If no initial conditions are given, obtain n linear equations in n unknowns and solve them, if possible, to get total solutions.

If y(h) denotes the homogeneous solution of the recurrence relation and y(p) indicates the particular solution of the recurrence relation then, the total solution or the general solution y of the recurrence relation is given by

Y = y(h) + y(p)

Example 1: solve the difference equation to find the total solution  ar - 4ar-1 + 4 ar-2 = 3r + 2r…..equation(1)

Solution: the homogenous of this equation is obtained by putting R.H.S equal to zero i.e., ar - 4ar-1+ 4ar-2 = 0

Then equation (1) can be written as,

(E2 - 4E + 4)ar = 3r + 2r

The particular solution is given as

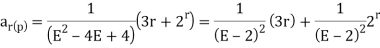
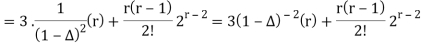
Therefore, the total solution is  ar = (c1 + c2r)2r + 3(r+2) + r(r-1)2r – 3

 Applications of relations and functions

Example 1: Suppose the weights of four students are shown in the following table.

Solution:  The pairing of the student number and his corresponding weight is a relation and can be written as a set of ordered-pair numbers.

W = {(1,120),(2,100),(3,150),(4,130)}

The set of all first elements is called the domain of the relation.

The domain of W = {1,2,3,4}

The set of second elements is called range of the relation.

The range of W = {120,100,150,130}

Example 2: Determine whether the following are functions

a)  A = {(1,2), (2,3), (3,4), (4,5)}

b)  B = {(1,3), (0,3), (2,1), (4,2)}

c)  C = {(1,6), (2,5), (1,9), (4,3)}

Solution:  a) A = {(1,2), (2,3), (3,4), (4,5)} is a function because all the first elements are different.

b)  B = {(1,3), (0,3), (2,1), (4,2)} is a function because all the first elements are different. (The second element does not need to be unique)

c)  C = {(1,6), (2,5), (1,9), (4,3)} is not a function because the first element, 1, is repeated.

A function can be identified from a graph. If any vertical line drawn through the graph cuts the graph at more than one point, then the relation is not a function. This is called the vertical line test.

4.4 Solving Recurrence Relations by Substitution and Generating Functions

Solution of recurrence relations by the method of generating functions

Any numeric function that can be described by a recurrence relation together with an appropriate set of boundary conditions is called a solution of the recurrence relation.

If

a = {a0, a1, a2, a3, . . . . , ar, . . . }  

Is a solution to a recurrence relation then it is said to satisfy the relation.

A given recurrence relation may or may not have a solution.

Method of generating functions-

Recurrence relations can also be solved by using generating functions. Some equivalent expressions used are given below-

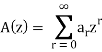
Then

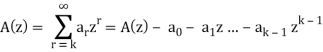
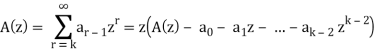
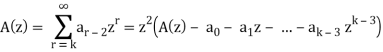
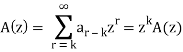
Example:  Solve the recurrence relation-

ar - 7ar-1 + 10ar-2 = 0 for r ≥ 2

Sol.

Multiplying each term of the recurrence relation by zr , we find-

arzr - 7ar - 1 zr + 10 ar - 2 zr = 0

Now taking the sum to 2 to ∞, we get

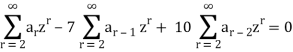
Replace each infinite sum by the corresponding equivalent expression given above, we obtain-

[A(z) - a0 - a1 z] - 7 z [ A(z) - a0] - 10 z2 A(z) = 0

On simplifying, we obtain-

A(z) (1 - 7z + 10 z2) = a0 + a1 z - 7 a0 z

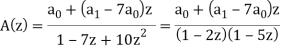
Decomposing A (z) as a sum of partial fractions, we can write

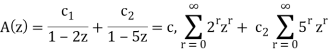
The solution is-

ar = c1 2r + c2 5r

4.5 The Method of Characteristic Roots

Consider a homogeneous second-order recurrence relation with constant coefficients which has the form

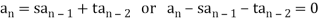
Where s and t are constants with t 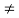0.We associate the following quadratic polynomial with the above recurrencerelation

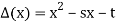
This polynomial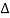(x) is called the characteristic polynomial of the recurrence relation, and the roots of (x)are called its characteristic roots.

Theorem: Suppose the characteristic polynomial 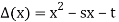of the recurrence relation

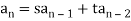
Has distinct roots r1 and r2. Then the general solution of the recurrence relation follows, wherec1 and c2 are arbitrary constants:

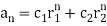
We emphasize that the constants c1 and c2 may be uniquely computed using initial conditions.

We note thatthe theorem is true even when the roots are not real.

Example: Consider the following homogeneous recurrence relation:

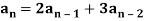
The general solution is obtained by first finding its characteristic polynomial 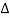(x) and its roots r1 and r2:

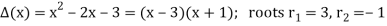
Since the roots are distinct, we can use Theorem mentioned above to obtain the general solution:

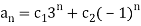
Thus any values for c1 and c2 will give a solution to the recurrence relation.

Suppose we are also given the initial conditions a0 = 1, a1 = 2. Using the recurrence relation we cancompute the next few terms of the sequence:

1, 2, 8, 28, 100, 356, 1268, 3516, . . .

The unique solution is obtained by finding c1 and c2 using the initial conditions. Specifically:

For n = 0 and 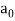= 1, we get:-

For n = 1 and 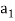= 2, we get:-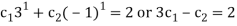

Solving the system of the two equations, we get

Thus the following is the unique solution of the given recurrence relation with the given initial conditions a0 = 1, a = 2:

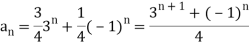
Solution when Roots of the Characteristic Polynomial are Equal:

Suppose the roots of the characteristic polynomial are not distinct. Then we have the following result.

Theorem:

Suppose the characteristic polynomial

Of the recurrence relation-

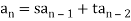
Has only one root r0. Then the general solution of the recurrence relation follows, where c1 andc2 are arbitrary constants:

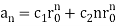
The constants c1 and c2 may be uniquely computed using initial conditions.

Example: Consider the following homogeneous recurrence relation-

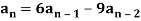
The characteristic polynomial 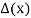follows:

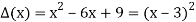
Thus 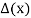has only the one root r0 = 3. Now we use Theorem 6.9 to obtain the following general solution ofthe recurrence relation:

Thus any values for c1 and c2 will give a solution to the recurrence relation.

Suppose we are also given the initial conditions a1 = 3, a2 = 27. Using the recurrence relation we cancompute the next few terms of the sequence:

3, 27, 135, 567, 2187, 8109, . . .

The unique solution is obtained by finding c1 and c2 using the initial conditions. Specifically:

For n = 1 and a1 = 3, we get:-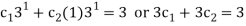

For n = 2 and a2 = 27, we get:-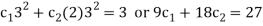

Solving the system of the two equations, we get

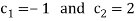
Thus the following is the unique solution of the recurrence relation with the given initial conditions:

4.6 Solutions of Inhomogeneous Recurrence Relations

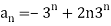
Any solution to therecurrence relation is the sum of two parts: the Homogenous solution and the particular solution. Asolution that satisfies the recurrence relation when the right hand side of the recurrence relation is set tozero is called a Homogeneous solution. The solution which satisfies the recurrence relation with f (r) onright hand side is called the particular solution. The homogeneous solution is denoted by 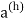and theparticular solutions denoted by 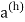. We follow the same procedure as in solving homogeneous recurrencerelations for determining the homogeneous solution. But there is no general procedure for determiningthe particular solution. It depends on the nature of f (r). The methods are described in terms of examples.(i) When f (r) is a constant. Then the particular solution is also a constant.

Example: Find the particular solution of the recurrence relation

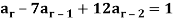
Sol:

f (r) is a constant. Therefore, the particular solution is also a constant P. Substituting P in thegiven equation, we get P – 7P + 12P = 1

We obtain-

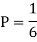
The particular solution is

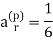
(ii) f (r) may be polynomial in r and is of degree m. Say. In this case the corresponding particularsolution is of the form

Example: Find the particular solution of

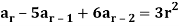
Sol:

Let the form of the particular solution be P1r2 + P2r + P3 where P1, P2 and P3 are constantsto be determined. Substituting the expression into the left hand side of given difference equation, we get

p1 r2 + P2 r + P3 + 5P1(r - 1)2 + 5 P2 (r -1) +5 P3 + 6P1 (r - 2)2 + 6P2 (r -1) + 6P3 = 3r2

Simplifying, we get

12P1 r2 - (34p1 - 12p2)r + (29P1 - 17P2 + 12P3) = 3r2

12P1 = 3                                                         .......(i)

34P1 - 12P2 =0                                              .......(ii)

29P1 - 17P2 + 12P3 = 0                                ........(iii)

Solving we get

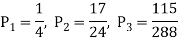
The particular solutions is-

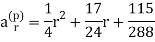
(iii) When f (r) is of the form and 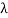is not a characteristic root of the recurrence relation, theparticular solution is of the form Pfurther more when f (r) is of the form

(b1 rm + b2 rm - 1 + . . . + bm+1) λr the corresponding particular solution is of the form

(P1 rm + P2 rm -1 + . . . + Pm + 1) λr

Where 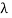is not a characteristic root of the recurrence relation. When 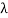is a characteristic root with

Multiplicity and f (r) is of the form

(b1rm + b2 rm - 1 + . . . + bm + 1)λr

The corresponding particular solution is of the form

rp - 1 (P1 rm + P2 rm - 1 + . . . + Pm + 1)λr

Example: Find a general expression for a solution to the recurrence relation-

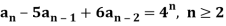
Sol:

The characteristic equation of the given relation is

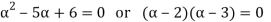
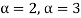are the characteristic roots

The homogeneous solution is

an(h) = A1 2n + A2 3n

The particular solution will be of the form

an(p) = λ. 4n

Putting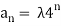

an - 5an - 1 + 6an - 2 = 4n

We get

λ4n - 5 λ 4n - 1 + 6 λ 4n - 2 = 4n

4n - 2[λ 42 - 5λ . 4 + 6λ] = 4n - 2 . 42

16λ - 20λ + 6λ = 16

2λ = 16

λ = 8

Therefore, the general solution of the given recurrence relation is

an = A1 . 2n + A2 3n + 8. 4n

References:

1. Discrete Mathematics and its Applications, Kenneth H. Rosen, 7th Edition, McGraw HillEducation (India) Private Limited.

2. Discrete Mathematics D.S. Malik & K. K. Sen, Revised Edition Cengage Learning.

3. Elements of Discrete Mathematics, C.L. Liu and D.P. Mohapatra, 4th Edition, McGraw HillEducation (India) Private Limited.

4. Discrete Mathematics with Applications, Thomas Koshy, Elsevier.