Unit - 3
Elementary Combinations
Sum rule-
Suppose S be a set and | S | denote the number of elements in S.
If S is a union of disjoint non-empty subsets
A1, A2,…,An then-
|S| = |A1| + |A2| + … + |An|
In the above statement the subsets Ai of S are all disjoint i.e., they have no element in common. If Ai
A nd Aj an two subsets of S, then-
Ai ∩Aj= ∅i≠j
And we have
S = A1 ∪A2 ∪A3 ∪... ∪An
That is each element of S is exactly in one of the subsets Ai. In other words, the subsets A1, A2,…An is a partition of S. We now state the sum rule for counting events.
Let S be a sample space. Two events E1 and E2 of X are said to be mutually exclusive if the events have no elements in common. If E1, E2, E3, …En, are mutually exclusive events of S, then we can state
Sum rule for counting events as follows:
If E1, E2… En are mutually exclusive events of a sample space S and E1 can happen in m1 ways. E2 can happen in m2 ways…
En can happen in mn ways then E1 or E2 or … or En can happen m1 + m2 + …
+ mn ways.
Sum rule principle-
Let A and B are two disjoint sets, then-
n(A ∪ B) = n(A) + n(B)
Product rule principle-
Let A×B is the Cartesian product of two sets A and B, then-
n(A B) = n(A). n(B)
Example-1: How many ways can we draw a club or a diamond from a pack of cards?
Solution: As we know that there are 13 clubs and 13 diamonds in a pack of cards.
The number of ways a club or a diamond may be drawn 13 + 13 = 26.
Example-2: In how ways can be drawn an ace or a king from an ordinary deck of playing cards?
Solution:
Number of Aces in a pack = 4
Number of kings in a pack = 4
Number ways an Ace or a king can be drawn from the pack = 4 + 4 =
Product rule-
If E1, E2, …., En are events, and E can happen in m1 ways E2 can happen m2 ways, … En can happen in mn ways, then the sequence of events E, first followed by E2 followed by E3, . . ., followed by En can happenin m1 × m2 × … × mn ways
Example-1: In how many different ways one can answer all the questions of a true-false test consisting of 4 questions?
Solution: There are two ways of answering each of the 4 questions. Therefore by product rule the
Number of ways in which all the 4 questions can be answered-
= 2 × 2 × 2 × 2 = 16
Permutations-
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are- P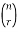
or nPr
Example 1: Consider the three letters x, y, z. The arrangements of the letter x, y, z taken two at a time are-
Xy, yx, xz, zx, yz, zy
∴The number of 2-arrangements are 6 i.e., the number of permutation of 3 letters taken 2 at a time
P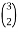
= 6
Note-A permutation of n objects taken r at a time is also called r-permutation
Factorial function-
The product of the positive integers from 1 to n is denoted by n! and we read it as “factorial “
Expressed as-
n! = 1.2.3.4…(n – 3)(n – 2)(n – 1)n
Note- 1! = 1 and 0! = 1n! = n(n – 1)!
Binomial coefficient-
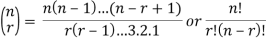
Example:
1. 
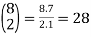
2. 
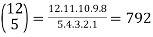
Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any r≤n of these objects in a given order is said to be r-permutation.
The number of permutations of n objects taken r will be denoted as-
P(n, r)
Formula- P(n, r) =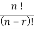 
Permutation with repetitions-
The number of permutations of n objects of which are q1 are alike, q2 are alike, qr
Are alike is-
P(n,q,q2, . . ., qr) = n!/(q1! q2!...qr!)
Sampling with or without replacement-
Suppose we chose the samples with repetition, from example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition
Then the product rule tells us that the number of such samples is-
n.n.n.n.n……….n.n = nr
And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.
So that in this case the number of samples are given as-
P(n, r) = n!/(n – r)!
Example-
Three cards are chosen one after the other from a 52-card deck. Find the number m of ways
This can be done: (a) with replacement; (b) without replacement.
Sol.
(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.
(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-
P(52, 3) = 52(51)(50) = 132 600
Example-
There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?
Solution: Total number of balls = 4 black + 3 green + 5 red = 12
The black balls are alike,
The green balls are, and the red balls are alike,
The number of ways in which the balls can be arranged in a row = 12!/(4!3!5!) = 27,720
Example- A box contains 10 light bulbs. Find the number n of ordered samples of:
(a) Size 3 with replacement,
(b) Size 3 without replacement.
Solution:
(a) n= 10r = 103 = 10 10 10 = 1,000
(b) P (10, 3) = 10 × 9 × 8 = 720
Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.
Hence the number of circular permutations of n different objects = (n – 1)!
Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
Note-
1. Property-1
C(n, r) = P(n, r)/r!
2. Property-2
C(n, n) = n!/(n!(n – n)!) = n!/(n!0!) = 1
3. Property-3
C(n, 0) = n!/(0!(n – 0)!) = n!/(0!n!) = 1
Combination of n things taking any number of them at a time when all the things are different:
Each one of the n different things may either be selected or not selected i.e., there are two ways of selecting for each one of the n things.
∴ The total number of combinations of n things taking any number of things is 2n.
But this includes the case in which all the things are rejected.
Hence the total number of ways in which one or more things are taken.
Corollary:
The total number of combinations of n things taken 1, 2, 3, …, n at a time i.e., C (n, 1) + C (n, l) + … +
C (n, n) =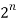 
– 1.
Example: In how many ways can a person invite one or more of his 5 friends to a party?
Solution: For every friend there are two possibilities i.e., he may be invited or he may not be invited to attend the party.
The number of ways in which we can invite his five friends at a party is 25.
But this includes the case when none of his friend is invited.
Hence, the number of ways in which he invites one or more of his five friends to a party is
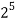– 1 = 32 – 1 = 31
Combination of n things taking any number of them at a time when all the things are not different:
Suppose that out of m + n + p + …, things m are alike, and of one kind, n are alike and of second kind and the rest are different, say they are k in number.
Out of m things we may take 0, 1, 2, … or m. Hence there (m + 1) ways of selecting the m things similarly, n things which are alike may be selected in (n + 1) ways and, P things which are alike may be selected in (P + 1) ways the remaining k different things may be selected in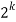 
ways. These include the case in which all are rejected.
∴ The total numbers of combinations
= (m + 1) (n + 1) (p 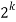+ 1) 
– 1
Basic identities:
Example: Prove that C (n, r) = C (n, n – r)
Sol:
C (n, r) denotes the number of selections of n objects when r-things are selected, and the remaining (n – r) objects are not selected. Therefore, selecting of r-things is the same as discarding (n – r) objects. For each selection of r things i.e., for each r-combination there is a discarding of n – r, remaining objects. The number of ways in which we discord (n – r) objects is C (n, n – r).
Since the set of r-combinations and the set of discarding of (n – r) objects are in one-one corresponding we get
C (n, r) = C (n, n – r)
Example: (Pascal’s Identity)
Show that C (n, r) = C (n – 1, r – 1) + C (n – 1, r)
C (n, r) is the number of r-combinations of n objects. Let n be any one of the n objects. Fix the object x the C (n, r) combinations can be grouped into:
(i) Those r-combinations that contain the objects x.
(ii) Those r-combinations that do not contain the object x.
Since the objects x is in all r-combinations of (i) we are to choose (r – 1) objects in each combinations of (i) from the remaining (n – 1) objects, this can be done in C (n – 1, r – 1) ways.
The number of combinations that contain x, is
C (n – 1, r – 1)
To count the number of r-combinations of (ii) i.e., the number of r-combinations which do not contain x, we omit the objects x from n objects and choose r objects from the remaining (n – 1) objects.
Therefore, the number r-combinations that do not contain x is C (n – 1, r).
Thus C (n, r) = C (n – 1, r – 1) + C (n – 1, r)
Example: (Pascals row sum identity)
Show that C (n, 0) + C (n, 1) + … + C (n, n) =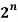 
Sol:
This is equivalent to finding the number of subsets of a set A with n elements. The number of subsets of A can be considered as follows:
The number of subsets having no elements (i.e., subsets with 0 elements is C (n, 0)
The number of subsets having 1 elements is C (n, 1) …
The number of subsets with n elements is C (n, n). Adding we get the number of elements in the power set of A.
i.e., | (A) | = C (n, 0) + C (n, 1) + … + C (n, n)
But the number of elements in the power set of A is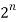 
.
Hence C (n, 0) + C (n, 1) + … + C (n, n) =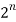 
Ordered partition:
A partition a non-empty set is called an ordered partition of S if there is a specified order on the subsets of S.
An ordered t-tuple of sets {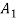
, 
, …, 
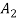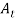} is called a t-part ordered partition if the sets 
, 
, …, 
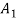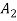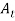form a partition of S.
Theorem:
Let S contain n distinct objects. Then the number of ways S can be partitioned in r
Subsets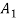 
, 
, …, 
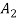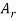with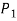 
objects in 
, 
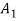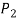objects in 
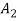…, and 
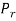objects in 
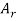is
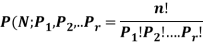
Example: A farmer buys 4 cows, 2 goats and 5 ducks from a person who has 7 cows, 5 goats and 8 ducks. How many choices the farmer have:
Sol:
The farmer can choose 4 cows from 7 cows in C (7, 4) ways, 2 goats from 5 goats in C (5,
2) ways and 5 ducks from 8 ducks in C (8, 5) ways.
∴ The farmer can choose 4 cows, 2 goats and 5 ducks in C (7, 4) C (5, 2) C (8, 5)
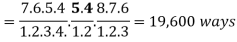
Example: There are twelve students in a class. Find the number of ways that the twelve students take three different tests if four students are to take each test.
Sol:
We find the number of ordered partitions of twelve students into cells containing four students each. There are
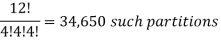
The required number of ways, the students can write the take the tests is 34,650.
Generalized sum rule-
If we have tasks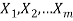 
that can be done in 
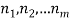ways respectively, and no two of these tasks can be done at the same time then there are 
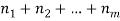ways to do one of these task.
Generalized product rule-
If we have sequential task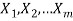 
that can be done in 
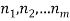, then there are 
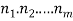to do the procedure.
Permutation and combination with unlimited repetitions-
Suppose U (n, r) denotes r-permutations of n-objects with unlimited repetitions and v (r, n) denotes the r-combination with unlimited repetitions, then-
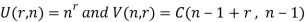
Let us consider a set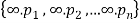 
where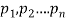 
are all distinct.
Any r-combination is of the form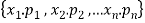 
here each 
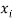is a non-negative integer and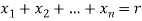 
The numbers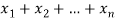 
are called repetition numbers. Conversely any sequence of non-negative integers-
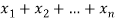
Corresponds to a r-combination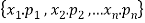 
.
The following observation we get-
The number of r-combination of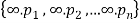 
= the number of non-negative integer solution of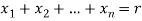 
= the number of ways of placing r indistinguishable balls in n numbered boxes.
= the number of binary numbers with n – 1 one’s and zeros.
= C (n – 1 + r, r)
= C (n – 1 + r, n - 1)
Example: Find the number of non-negative integral solutions to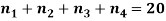 
Sol: We have n = 4, r = 20
The number of non-negative integral solutions
= C (4 – 1 + 20, 20)
= C (23, 20)
= 1,771
Example-Find the number of ways of placing 8 similar balls in 5 numbered boxes.
Solution:
The number of ways of placing similar balls in 5 numbered boxes is
= C (5 – 1 + 8, 8)
= C (12, 8) = 495
Example-How many outcomes are possible by costing a 6 faced die 10 times?
Solution:
This is same as placing 10 similar balls into 6 numbered boxes.
There are C (6 – 1 + 10, 10)
= C (15, 10) possible outcomes.
Let U(n, r) denote r-permutations of n-objects with unlimited repetitions, and v (n, r) denote the number of r-combinations with unlimited repetitions, then
U(n, r) =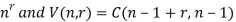 
Consider t he set {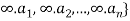
where a1, a2, …, an are all distinct. Any r-combination is of the form {
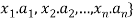where each xi is a non-negative integer and x1 + x2 + … + xn = r.
The numbers x1 + x2 + … + xn are called repetition numbers. Conversely any sequence of non-negative integers
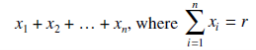
Corresponds to a r-combination {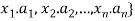
The following observations are made:
The number of r-combinations of {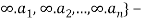
= The number of non-negative integers solution of x1 + x2 + … + xn = r.
= The number of ways of placing r indistinguishable balls in n numbered boxes.
= The number of binary numbers with n – 1 one’s and r zeros.
= C (n – 1 + r, r)
= C (n – 1 + r, n – 1)
Example: Find the 4-combinations of {1, 2, 3, 4, 5, 6}.
Sol: The 4-combinations are 1234, 1235, 1236, 1245, 1246, 1256, 1345, 1346, 1356, 1456, 2345, 2346, 2456, 3456.
Example: Find the number of non-negative integral solutions to n1 + n2 + n3 + n4 = 20
Sol:
We have n = 4, r = 20
The number of non-negative integral solutions
= C (4 – 1 + 20, 20)
= C (23, 20) = 1,771
Example: Find the number of ways of placing 8 similar balls in 5 numbered boxes.
Sol: The number of ways of placing similar balls in 5 numbered boxes is
= C (5 – 1 + 8, 8)
= C (12, 8) = 495
Example: Find the number binary numbers with five 1’s and three 0’s.
Sol: The number of binary numbers with five 1’s and three 0’s is
= C (5 + 3, 3)
= C (8, 3)
= 56
Example: How many outcomes are possible by costing a 6 faced die 10 times?
Sol: This is same as placing 10 similar balls into 6 numbered boxes.
There are C (6 – 1 + 10, 10)
= C (15, 10) possible outcomes.
The numbers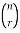
are called the binomial coefficients.
Binomial theorem-
Binomial theorem gives a formula for the coefficients in the expansion of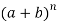 
.
According to theorem-
Let n be a positive integer then for all a and b, then
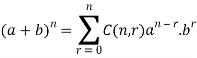
Example-1: Expand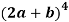 
Sol.
Here we have-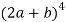
By using binomial theorem, we get
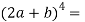
= C (4, 0)(2a)4 + C(4, 1)(2a)3b + C(4, 2) (2a)2b2 +C(4,3)(2a)b3+C(4,4)b4
=16a4 + 32a3b + 24 a2b2 + 8ab3 + b4.
Example-2: Find the term containing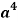 
in the expansion of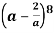 
Sol.
The general term will be-
Tr+1 = C(8, r) a8 – r(-2/a)r
= C(8, r) a8-r(-2a-1)r
= C (8, r)a8-r(-2)r(a-1)r
= C(8, r) (-2)ra8-ra-r
= C(8, r)(-2)ra8-2r
Put 8 – 2r = 4 we get r = 2
Therefore the term contain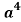s
is-
Tr+1 = T3 = C(8, r) (-r)ra4
= C (8, r) 4 a4
= 284 a4
=112 a4
Note-
If we replace ‘a’ and ‘b’ by ‘x’ and ‘1’ then we get another form of the binomial theorem-
(x + 1)n = 
Example-3: In the expansion of 
, prove the following result-
C02 + C12 + C22 + . . . + Cn2 = 2n!/(n!)2
Sol. We have-
(1+x)n = C(n, 0) + C(n, 1) x + . . . + C(n, n)xn
As we know that the coeff. Of the terms equivalent from the beginning and end are equal, so that-
(1+x)n = C(n, n) + C(n, n -1) x + . . . + C(n, 0)xn
By multiplying the above two equations, we get-
(1+x)2n = [C(n, 0) + C(n, 1) x + . . . + C(n, n)xn]x[C(n, n) + C(n, n – 1)x + . . . + C(n, 0)]xn
From RHS, we see the coeff. Of
C(n, 0)2 + C(n, 1)2 + . . . + C(n, n)2
But the coeff. Of
in 
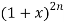is-
C(2n , n) = 2n!/n!.n! = 2n!/(n!)2
C02 + C12 + Cn2 = 2n!/(n!)2
Example: If If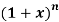 
= C (n, 0) + C (n, 1) x + C (n, 2) 
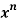+ … + C (n, n)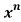
Prove that C (n, 1) + 2 C (n, 2) + 3 C (n, 3) + … + n C (n, n) = n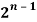 
.
Sol:
C(n, 1)x + 2 C (n, 2) x2 + . . . + n C (n, n) xn
= nx + 2 . 2(n – 1)/2! x2 + . . . + n xn
= nx + n(n – 1) x2 + . . . + nxn
= nx[1 + (n – 1)x + . . . + xn-1]
= nx[ C(n – 1, 0) + C(n – 1, 1) x + . . . + C(n – 1, n – 1) xn – 1]
= nx(1+x)n -1
Example: Prove that
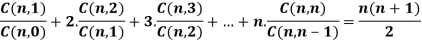
Sol:
We know that
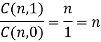
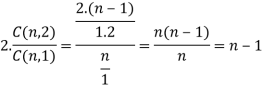
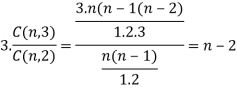
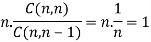
Adding, we get
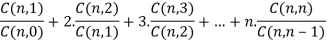
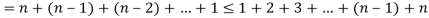
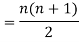
Note-
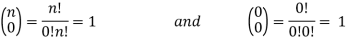
And
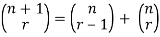
Multi-Nominal Theorems:
Let n be a positive integer, then for all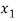 
+ 
+ … + 
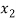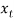
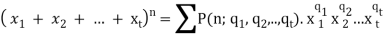
Where the summation extends over all sets of non-negative integers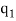 
, 
, …, 
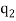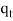
Where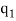 
+ 
+ … + 
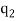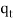= n.
Example: Find the coefficients of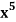 
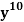
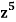
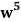in the expansion of 
.
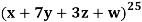Sol:
We have n = 25, x1 = x1, x2 = 74, x3 = 3 z, and x4 = w
∴ The coefficients of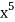 
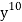
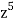
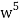in the expansion of 
.
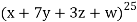Is
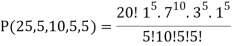
The Inclusion-Exclusion principle can be stated as below-
Let A and B any two finite sets, then-
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Meaning- Here if we have to find the number n(A∪B) of elements in the union of A and B.
So then we add n(A) and n\(B) which means we are including these two.
And then we exclude n(A∩B).
Note- For three sets-
If we have three finite sets A, B and C then-
n(A ∪ B ∪ C) = n (A) + n( B) + n(C) – n(A ∩B) – n(A∩C) – n(B∩C) +n(A∩B∩C)
Example: Find the number of students at a college choosing at least one of the subject from mathematics, physics and statistics.
The data is given as-
65 study maths, 45 study physics, 42 study statistics
20 study maths and physics, 25 study maths and statistics, 15 study physics and statistics and 8 study all the three subjects.
Sol.
Here we need to find n(M∪P∪S) where,
M = maths, P = physics and S = statistics
Now by using Inclusion-Exclusion principle-
n(M ∪ P ∪ S) = n(M) + n(P) + n(S) – n(M ∩ P) – n(M ∩ S) – n(P ∩ S) + n(M ∩ P ∩ S)
Which gives-
n(M ∪ P ∪ S) = 65 + 45 + 42 – 20 – 25 – 15 + 8 = 100
Therefore, we find that 100 students study at least one of the three subjects.
References:
1. Discrete Mathematics and its Applications, Kenneth H. Rosen, 7th Edition, McGraw Hill Education (India) Private Limited.
2. Discrete Mathematics D.S. Malik & K. K. Sen, Revised Edition Cengage Learning.
3. Elements of Discrete Mathematics, C.L. Liu and D.P. Mohapatra, 4th Edition, McGraw Hill Education (India) Private Limited.
4. Discrete Mathematics with Applications, Thomas Koshy, Elsevier.
5. Discrete and Combinatorial Mathematics, R. P. Grimaldi, Pearson.
