Unit - 2
Set Theory
A collection of unique things of the same type or class of objects is referred to as a set. A set's goals are referred to as its elements or members. Numbers, alphabets, names, and other objects are examples of objects.
Sets- A set is a collection of well-defined objects which are called the elements or members of the set.
We generally use capital letters to denote sets and lowercase letters for elements.
If any element which exists in the set is to be denoted as-
Suppose an element ‘a’ is from a set X, then it is represented as- aX
Which means the element ‘a’ belongs to the set X.
If the element is not form the group then we use ‘not belongs to’.
Examples of sets are:
- A set of rivers of India.
- A set of vowels.
A set is denoted by the capital letters A, B, C, and so on, whereas the basics of the set are denoted by the small letters a, b, x, y, and so on.
If A is a set and an is one of its elements, we refer to it as an a ∈ A. "Element of" is the meaning of the sign ∈ in this case.
Set Representation
There are two ways to express a set:
a) Roster or tabular form: We list all the components of the set within braces {} and separate them with commas in this type of representation.
For example, if A is a set of all odd numbers less than 10, then A= {1,3,5,7,9} can be written in the roster.
b) Set Builder form: In this representation, we list all of the qualities that all of the set's elements satisfy. We write as {x: x satisfies properties P}. and can be read as 'the set of all x such that each x has the attributes P.'
For example, If B= {2, 4, 8, 16, 32}, the set builder representation will be: B={x: x=2n, where n ∈ N and 1≤ n ≥5}.
Subsets-
Let every element of set X is also an element of a set Y, then X is said to be the subset of Y.
Symbolically it is written as-
X ⊆ Y
Which is read as- X is the subset of Y.
Note- If X = Y then X ⊆ Y and Y ⊆ X
Proper sub-set-
A set X is called proper subset the set Y is-
1. X is subset of Y
2. Y is not subset of X
Note- every set is a subset to itself.
Equal sets-
If X and Y are two sets such that every element of X is an element of Y and every element of Y is an element of X, the set and set Y will be equal always.
We write it as X = Y and read as X and Y are identical.
Super set-
If X is a subset of Y, then Y is called a super set of X.
Null set-
A set which does not contain any element is known as null set.
We denote a null set by ∅
The null set is a subset of every set.
Singleton-
A set which has only one element is called singleton.
Example- A = {10} and B = {∅}
Theorem- if ∅ and ∅’ are empty sets then ∅=∅’
Proof: Let ∅≠ ∅’ then the following conditions must be true-
1. There is element x∈∅ such that x∉∅’
2. There is element x∈∅’ such that x∉∅.
But both these conditions are false since ∅’ and ∅’ has any elements if follows that ∅=∅’.
Operations on sets
1. Union and intersection-
Union-We denote union of two sets as- A∪B, which is the set of all elements which belongs to A or to B.
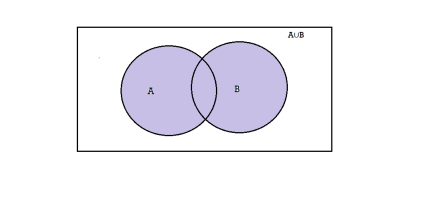
That is-
A∪B = {x |x∈∅A or x∈∅B}
Intersection- We denote intersection of two sets as- A∩B, which is the set of all elements which belongs to A and to B.
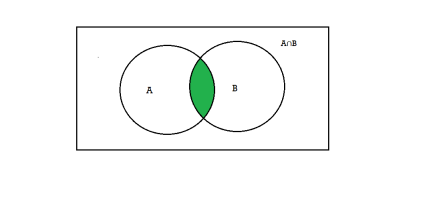
That is-
A∩B = {x |x∈∅A and x∈∅B }
Note- Two sets are said to be disjoint if they have no common elements in common.
Example: If A = {1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8, 9} and C = {5, 6, 7, 8, 9, 10}
Then-
A∪B = {1, 2, 3, 4, 5, 6,7, 8, 9}
A∪C = {1, 2, 3, 4, 5, 6,7, 8, 9,10}
B∪C = {4, 5, 6,7, 8, 9, 10}
A∩B = {4, 5, 6}
A∩C = {5, 6}
B∩C = {5, 6, 7, 8, 9}
Property-1-
An element x belongs to the union A∪B if x belongs to A or x belongs to B; hence every element
In A belongs to A ∪B, and every element in B belongs to A ∪B. That is,
A ⊆A ∪B and B ⊆A ∪B
Property-2-
An element x belongs to the union A∪B if x belongs to A or x belongs to B; hence every element
In A belongs to A ∪B, and every element in B belongs to A ∪B. That is,
A ⊆A ∪B and B ⊆A ∪B
Complements, differences and symmetric differences-
Complement-
The complement of a set A, denoted by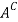 , is the set of elements which belong to U(universal set)but which do not belong to A. That is
, is the set of elements which belong to U(universal set)but which do not belong to A. That is
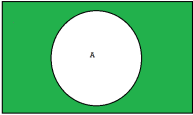
 = {x | x ∈U, x /∈A}
= {x | x ∈U, x /∈A}
Difference-
The difference of A and B, denoted by A\B or A-B, is the set of elements which belong to A but which do not belong to B that is-
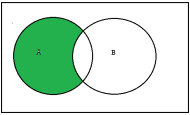
A-B = {x | x ∈A, x / ∈B}
The set A\B or A-Bis read “A minus B”.
Symmetric difference-
The symmetric difference of sets A and B, denoted by A⊕B, consists of those elements which belong to A or B but not to both. That is
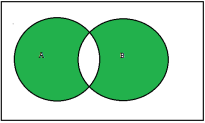
A ⊕B = (A ∪B)-(A ∩B) or A ⊕B = (A-B) ∪(B-A)
Cardinality of sets-
If A is finite set with n distinct elements, then n is called the cardinality of A. The cardinality of A is denoted by |A| [or by n (A)].
Example: Let A = {a, b, c, d}, then A is a finite set and |A| = 4
Cardinality of union of two sets-
Number of elements in A ∪B: (Cardinality of union) If A and B are any two finite sets then, the numbers of elements in A ∪B, denoted by | A ∪B | is given by | A ∪B | = | A | + | B | −| A ∩B |
Principal of inclusion and Exclusion-
Let we have A and B are finite sets. Then A ∪B and A ∩B are
Finite and
n(A ∪B) = n(A) + n(B) −n(A ∩B)
That is, we find the number of elements in A or B (or both) by first adding n(A) and n(B) (inclusion) and then
Subtracting n(A ∩B) (exclusion) since its elements were counted twice
For three sets-
n(A ∪B ∪C) = n(A) + n(B) + n(C) −n(A ∩B) −n(A ∩C) −n(B ∩C) + n(A ∩B ∩C)
Key takeaway
- A collection of unique things of the same type or class of objects is referred to as a set.
- A set's goals are referred to as its elements or members.
- Numbers, alphabets, names, and other objects are examples of objects.
Ordered pair-
An ordered pair of element a and b, where a is designated as the first element and b as the second element, it is denoted by (a, b).
In particular
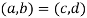
If and only if a = c and b = d. Thus
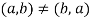
Unless a = b.
n-tuple-
A finite sequence over a set A is a function from {1, 2,….,n} into A, and it is usually denoted by
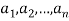
Such a sequence which is finite is called an n-tuple.
Here ‘n’ is a non-negative integer.
Tuples are written by listing the elements with parentheses ().
Cartesian product
Suppose we have two sets A and B, then we can form the set-
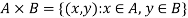
To be the set of all ordered pairs (x,y) where x is an element of A and y is an element of B.
Here we call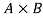 the Cartesian product of A and B.
the Cartesian product of A and B.
Example: If A = {1, 2} and B = {3, 4, 5} then find 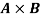 .
.
Sol.
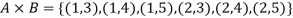
Example: Let A = {1, 2} and B = {a, b, c}, then-
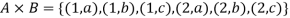
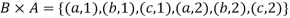
And
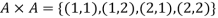
Note-
1. 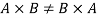
2. 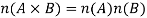
A1 A2 . . . An or 
3. The Cartesian product of two sets of real numbers can be represented by tree diagrams.
Theorems-
If A, B, C are sets then-
1. 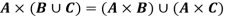
2. 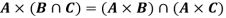
Proof-
1.
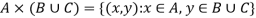
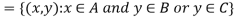
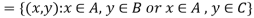
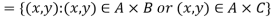
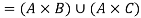
2.
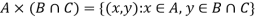
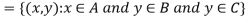
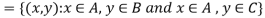
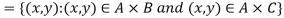
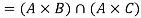
Theorem-
If A, B, and C are non-empty sets then A ⊆B ⇒A × C ⊆B × C
Proof: Let (a, b) be any element A × C, then
⇒a∈B and b ∈C (because A ⊆B)
⇒ (a, b)∈B × C
Hence A × C ⊆B × C
Cartesian product of n-sets-
Let 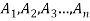 denote n sets where n ≥2 , then the Cartesian product
denote n sets where n ≥2 , then the Cartesian product 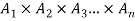 is the set ofall n-tuples of the form
is the set ofall n-tuples of the form 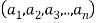 where
where 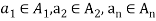
From the definition we have
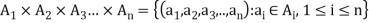
Definition and Properties
Let P and Q be two sets that aren't empty. A subset of P x Q from a set P to Q is defined as a binary relation R. If (a, b) ∈ R and R ⊆P x Q, then a and b are connected by R, i.e., aRb. When the sets P and Q are equivalent, we say R ⊆P x P is a relation on P, for example
(i) Let A = {a, b, c}
B = {r, s, t}
Then R = {(a, r), (b, r), (b, t), (c, s)}
Is a relation from A to B.
(ii) Let A = {1, 2, 3} and B = A
R = {(1, 1), (2, 2), (3, 3)}
Is a relation (equal) on A.
Example - How many relations exist between A and A if a set has n elements?
Solution -
A x A has n2 items if the set A has n elements. As a result, there exist 2n2 relationships between A and A.
Domain of relation - The set of elements in P that are related to some elements in Q, or the set of all initial entries of the ordered pairs in R, is the domain of relation R. DOM is the abbreviation for it (R).
Range of relation - The scope of the relationship R is the set of all second entries of the ordered pairs in R, alternatively it is the set of all elements in Q that are connected to some element in P. RAN is the abbreviation for it (R).
Example: Let A = {1, 2, 3, 4}
B = {a, b, c, d}
R = {(1, a), (1, b), (1, c), (2, b), (2, c), (2, d)}.
Solution:
DOM (R) = {1, 2}
RAN (R) = {a, b, c, d}
Operation on relation
A subset of the Cartesian product of A and B is a binary relation between two nonempty sets A and B (in that order) (in that order). Because relations are sets, they can be affected by standard set operations. For example, given two relations R1 and R2, we can compute their union, intersection, and difference.
Union of two relations
Given two relations R1 and R2, the union of these relations, represented by R1∪ R2, will be defined as
R1∪ R2 ab R ab R = {(a, b) / (a, b) ∈ R1∨ (a, b) ∈ R2}
Intersection of two relations
Given two relations R1 and R2, we shall define R1∩ R2 as the intersection of these two relations.
R1∩ R2 = {(a, b) / (a, b) ∈ R1∧ (a, b) ∈ R2}
Difference of two relations
We will define the difference of relations R1 and R2 (in that order), represented by R1– R2, as follows:
R1− R2 = {(a, b) / (a, b) ∈ R1∧ (a, b) ∉ R2}
Key takeaway
- The set of elements in P that are related to some elements in Q, or the set of all initial entries of the ordered pairs in R, is the domain of relation R.
- The scope of the relationship R is the set of all second entries of the ordered pairs in R.
- A subset of the Cartesian product of A and B is a binary relation between two nonempty sets A and B (in that order).
It's a mapping in which each element in set A is linked to a specific element in set B. The domain of a function is the set of A, and the domain of B is the set of B.
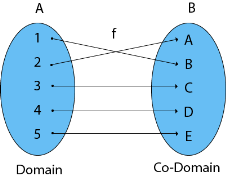
Fig: Domain and co-domain
Domain, Co-domain, and Range of function
Domain - Let f be a function that goes from point P to point Q. The domain of the function f is the set P.
Co-domain - Let f be a function that goes from point P to point Q. The set Q is referred to as the function f's Co-domain.
Range - The collection of pictures in a function's domain is its range. To put it another way, it is a subset of its co-domain. The letter f is used to represent it (domain).
If f: P → Q, then f (P) = {f(x): x ∈ P} = {y: y ∈ Q | ∃ x ∈ P, such that f (x) = y}.
Example: Find the function's Domain, Co-Domain, and Range.
Let x = {1, 2, 3, 4}
y = {a, b, c, d, e}
f = {(1, b), (2, a), (3, d), (4, c)
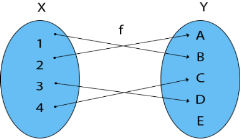
Solution: Domain of function: {1, 2, 3, 4}
Range of function: {a, b, c, d}
Co-Domain of function: {a, b, c, d, e}
Classification of functions
1. Injective (One-to-One) Functions: One element of the Domain Set is associated to one element of the Co-Domain Set in this function.
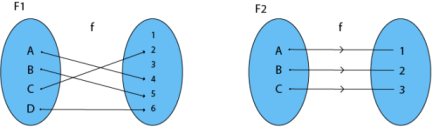
Fig: f1 and f2 show one to one function
2. Surjective (Onto) Functions: Every element of the Co-Domain Set has one pre-image in this function.
Example: Consider, A = {1, 2, 3, 4}, B = {a, b, c} and f = {(1, b), (2, a), (3, c), (4, c)}.
Because every element of B is the image of some A, it is a Surjective Function.
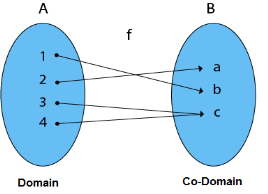
Fig: Surjective function
3. Bijective (One-to-One Onto) Functions: Bijective (One-to-One Onto) Function is a function that is both injective (one to one) and surjective (onto).
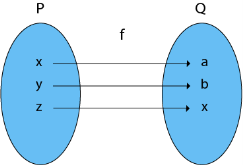
Fig: One to one function
Example: Consider P = {x, y, z}
Q = {a, b, c}
And f: P → Q such that
f = {(x, a), (y, b), (z, c)}
The f is both a one-to-one and an onto function. It is, thus, a bijective function.
4. Into Functions: There is no pre-image in domain X for a function that requires an element from co-domain Y.
Example: Consider, A = {a, b, c}
B = {1, 2, 3, 4} and f: A → B such that
f = {(a, 1), (b, 2), (c, 3)}
In the function f, the range i.e., {1, 2, 3} ≠ co-domain of Y i.e., {1, 2, 3, 4}
As a result, it is an into function.
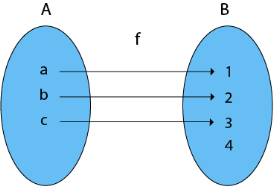
Fig: Into function
5. One-One Into Functions: Let f: X →Y be the case. If distinct elements of X have different unique images of Y, the function f is called one-one into function.
Example: Consider, X = {k, l, m}
Y = {1, 2, 3, 4} and f: X → Y such that
f = {(k, 1), (l, 3), (m, 4)}
The function f is a one-to-one conversion.
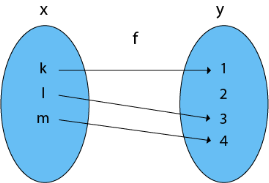
Fig: One one into function
6. Many-One Functions: Let f: X →Y be the case. If there are two or more separate items in X that have the same image in Y, the function f is said to be a many-one function.
Example: Consider X = {1, 2, 3, 4, 5}
Y = {x, y, z} and f: X → Y such that
f = {(1, x), (2, x), (3, x), (4, y), (5, z)}
The function f is a many to one
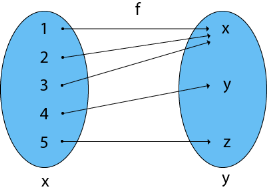
Fig: Many to one function
7. Many-One Into Functions: Let f: X→Y be the case. If and only if is both many one and into function, the function f is termed the many-one function.
Example: Consider X = {a, b, c}
Y = {1, 2} and f: X → Y such that
f = {(a, 1), (b, 1), (c, 1)}
Because f is a many-one and into function, it is also a many-one into function.
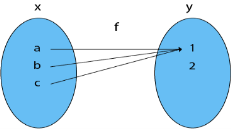
Fig: Many one into function
8. Many-One Onto Functions: Let f: X→ Y be the case. If and only if is both many one and onto, the function f is termed a many-one onto function.
Example: Consider X = {1, 2, 3, 4}
Y = {k, l} and f: X → Y such that
f = {(1, k), (2, k), (3, l), (4, l)}
The function f is a many-one (since the two elements in Y have the same image) and onto (as every element of Y is the image of some element X). As a result, it is a many-to-one function.
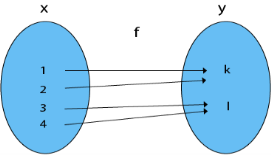
Fig: Many one onto function
Key takeaway
- It's a mapping in which each element in set A is linked to a specific element in set B.
- The domain of a function is the set of A, and the domain of B is the set of B.
Binary operations-
A binary operation * is a set A is a function from A × A to A.
If * is a binary operation in a set A then than for the * image of the ordered pair (a, b) ∈ A×A, we write a*b.
For example:
Addition + is a binary operation in the set of natural number N, integer Z and real number R.
Multiplication is a binary operation in N, Q, Z, R and C.
General properties-
Propery-1: Let A be any set. A binary operation * A × A →A is said to be commutative if for every a, a, b ∈A.
a* b = b * a
Property-2: Let A be a non-empty set. A binary operation *; A × A →A is said to be associative if
a* b) * c = a * (b * c) for every a, b, c ∈A.
Property-3: Let * be a binary operation on a non-empty set A. If there exists an element e ∈A such that e * a = a * e = a for every a ∈A, then the element e is called identity with respect to * in A.
Property-4: Let * be a binary operation on a non-empty set A and e be the identity element in A with respect the operation *. An element a ∈A is said to be invertible if there exists an element b ∈A such that
a* b = b * a = e
In which case a and b are inverses of each other. For the operation * if b is the inverses of a ∈A then we can write b = 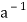
Cancellation laws-
A binary operation denoted by * in a set A, is said to satisfy.
(i) Left cancellation law if for all a, b, c ∈A,
a* b = a * c ⇒b = c
(ii) Right cancellation law if for all a, b, c ∈A
b* a = c * a ⇒b = c
Algebraic system-
If A is a set and * is a binary operation on A, then (A, *) is called an algebraic structure.
Example: Let R be the set of real numbers, then (R, +) is an algebraic structure.
Example: If N denotes the set of natural numbers then (N, +) is an algebraic structure.
An algebraic system is an object A = (A, O, R) consisting of a non-empty set A. a family O of algebraic operations Oi: Ani A (iI) and a family R of relations rj Amj (jJ) defined on A. The indices ni, mj of the Cartesian powers of A under the consideration are assumed to be non-negative integers and are said to be arities of the respective operations and relations. The set A is called the Cartesian set or underlying set of algebraic system A. While its elements are called the elements of this system. The cardinality |A| of A is said to be the cardinality of A or the order of the algebraic system A. The image Oi (a1, a2, . . . , ani) of the element (a1, a2, . . ., ani) ∈Ani
Under the mapping Oi :Ani A is called the value of operation Oi at the point (a1, a2, . . . , ani) .similarly, if (a1, a2, . . . , amj) ∈ ri, then one says that the elements (a1, a2, . . . , amj) of A are in relation rj , and one writes rj (a1, a2, . . . , amj) .The operations Oi ( i∈I) and the relation rj ( j ∈ J), unlike other operations and relations that may be defined on A , are called basic operation primitive.
Example: solve the following system of equations
2x + 3y + 2z = - 38 ….(1)
3x – 2y + 4z = 17 …..(2)
-6x + y – 7 z = - 12 … (3)
Solution:
(1) 3 6x + 15 y + 6z = - 114
(2) 2 6x – 4y +8z = 34
(3) - 6x +y – 7z = - 12
By solving the above equations we get
16y – z = - 126
-3y + z = 22
-6x + y – 7z = - 12
Solving for z we get
13y = - 104
-3y + z = 22
-6x + y -7z = - 12
We get y = -8
By putting y value in above equation we get z=-2
And inserting both the equations we solve for x, we get x= 3
Therefore the solution to the system of equation is x = 3, y = -8, z = -2
Semi-group-
Let S be a non-empty set and * be a binary operation on S. The algebraic (S, *) is called a semi-group if the operation * is associative. In other words, the groupoid is a semi-group if
(a* b) * c = a * (b * c) for all a, b, c ∈S
Thus, a semi-group requires the following:
(i) A sets.
(ii) A binary operation * defined on the elements of S.
(iii) Closure, a * b whenever a, b ∈S.
(iv) Associativity i(a * b) * c = a * (b * c) for all a, b, c ∈S.
Example: Let N be the set of natural numbers. Then (N, +) and (N, *) are semi-groups.
Homomorphism of semi-groups-
Let (S, *) and (T, 0) be any two semi-groups. A mapping f: S →T such that for any two elements a, b ∈S
f(a * b) = f (a) o f(b) is called a semi-group homomorphism.
Isomorphism of semi-groups-
Let (S, *) and (T, 0) be any two semi-groups. A homomorphism f: S →T is called a semi-group isomorphism if f is one-to-one and onto.
If f: S →T is an isomorphism then (S, *) and (T, 0) are said to be isomorphic.
Monoid-
A semi-group (M, *) with an identity element with respect to the binary operation * is called a monoid. In other words, an algebraic system (M, *) is called a monoid if:
(i) (a * b) * c = a * (b * c) ∀a, b, c ∈M.
(ii) There exists an element e ∈M such that e * a = a * e = a ∀a ∈M.
Example: Let Z be the set of integers (Z, +) is a monoid 0 is the identity element in Z with respect
To +.
Cyclic monoid-
A monoid (M, *) is said to be cyclic if there exists an element a ∈M. Such that every element of M can be expressed as some power of a. If M is a cyclic monoid such that every element is some power of
a∈M, then a is called the generator of M. A cyclic monoid is commutative and a cyclic monoid is commutative and a cyclic monoid may have more than one generator.
Monoid homomorphism-
Let (M, *) and (T, 0) be any two monoidsemand et denote the identity elements of
(M, *) and (T, 0) respectively. A mapping
f: M →T such that for any two elements a, b ∈M
f(a * b) = f (a) o f(b)
And
f(em ) = et
Is called a monoid homomorphism.
A group is an algebraic structure (G, *) in which the binary operation * on G satisfies the following conditions:
Condition-1: for all a, b, c, ∈G
a* (b * c) = (a * b) * c (associativity)
Condition-2: there exists an elements e ∈G such that for any a ∈G
a* e= e * a = a (existence of identity)
Condition-3: for every a ∈G, there exists an element denoted by a-1 in G such that
a*a-1= a-1* a = e
a-1 is called the inverse of a in G.
Example: (Z, +) is a group where Z denote the set of integers.
Example: (R, +) is a group where R denote the set of real numbers.
Abelian group-
Let (G, *) be a group. If * is commutative that is
a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.
Finite group-
A group G is said to be a finite group if the set G is a finite set.
Infinite group-
A group G, which is not finite is called an infinite group.
Order of a finite group-
The order of a finite group (G, *) is the number of distinct element in G. The order of
G is denoted by O (G) or by |G|.
Example: If G = {1, -1, i, -i} where i= -1, then show that G is an abelian group with respect to multiplication as a binary operation.
Sol.
First we will construct a composition table-
. | 1 | -1 | i | -i |
1 | 1 | -1 | i | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | i | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties holds.
∴Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied
Hence (G, ⋅) is an abelian group.
Example-
Prove that the set Z of all integers with binary operation * defined by a * b = a + b + 1 ∀a, b ∈G is an abelian group.
Sol: Sum of two integers is again an integer; therefore a +b ∈Z ∀a, b ∈Z
⇒a +b + 1 ⋅∈Z ∀a, b ∈Z
⇒Z is called with respect to *
Associative law for all a, b, a, b ∈G we have (a * b) * c = a * (b * c) as
(a* b) * c = (a + b + 1) * c
= a + b + 1 + c + 1
= a + b + c + 2
Also
a* (b * c) = a * (b + c + 1)
= a + b + c + 1 + 1
= a + b + c + 2
Hence (a * b) * c = a * (b * c) ∈a, b ∈Z.
Lattices-
A lattice is a partially ordered set (L, ≤) in which every pair of elements a,b ∈ L has a greatest lower bound and a least upper bound
For example-
Suppose S be a non-empty set and L = P(S); (P(S); ≤) that means (L, ≤) is partially ordered.
If X and Y are two elements of L, then-
A ∪ B = A ∨ B and A ∩ B = A ∧ B
Hence (L, ≤) is a Lattice.
Axiomatic definition of Lattice-
Let L be a non-empty set closed under two binary operations denoted by ∧ and ∨.
Then L is said to be a Lattice if it follows the axioms given below, here a, b and c are the elements of L.
1. Commutative law-
(i) a∧ b = b ∧ a (ii) a ∨ b = b ∨ a
2. Associative law-
(i) (a ∧ b) ∧ c = a ∧ ( b ∧ c) (ii) (a ∨ b) ∨ c = a ∨ (b ∨ c)
3. Absorption law-
(i) a∧ (a∨b) = a (ii) a∨(a∧b) = a
To show that which operation is involved we denote the Lattice by (L, ∧, ∨)
Theorem-Let (L, ≤) be a lattice in which ‘⋅’ And ‘+’ denote the operations of meet and join respectively.
Then
a≤b ⇔a ⋅b = a ⇔a + b = b ∀a, b, c ∈L
Proof: Suppose a ≤b
As we know that a ≤a so that a ≤a.b but according to definition a.b≤a
So that- a ≤b ⇒a ⋅b = a
Let a ⋅b = a
But this is possible only if a ≤b which means a ⋅b = a ⇒a ≤b
∴a≤b⇒a ⋅b = a and a ⋅b = a ⇒a ≤b
Combine these two, we get
a≤b ⇔a ⋅b = a
Now let,
a⋅b = a,
Then we have
b + (a ⋅b) = b + a + a + b
But,
b + (a ⋅b) = b
Hence a + b = b
Similarly by assuming a + b = b
We can show that a ⋅b = a
Hence a ≤b ⇔a ⋅b = a ⇔a + b = b = a
Isomorphic Lattice-
Two lattices L and L’ are said to be isomorphic if there is a one-to-one correspondence
f: L →L’
Such that
f (a ∧b) = f (a) ∧f (b) and f (a ∨b) = f (a) ∨f (b)
For any elements a, b in L.
Note-
1. A lattice is called complete if each of its non-empty subsets has a least upper bound and a greatest lower bound.
2. A lattice L is complemented if it is bounded and if every element in L has a complement.
3. Let ( L, ⋅, +, 0, 1) be a bounded lattice and a ∈L. If there exists an element b ∈L Such that a⋅b = 0 and a + b = 1
Then b is called the complement of a.
Sub Lattices and Direct products-
Sub Lattices-
Let (L, ≤) be a lattice. A non-empty subset A of L is called a sub lattice of L if a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
If A is a sub lattice of L, then A is closed under the operations of ‘’ ⋅and ‘+’.
Direct product-
Let (L1, *, +) and (L2,∧, ∨) be two lattices. The algebraic system (L1 × L2,...,+)
In which the binary operation + and ‘’ ⋅are on L1 × L2 defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 )
For all (a1, b1) and (a2, b2) (a2 ,b2 ) ∈L1 × L2
Is called the direct product of the lattices L1 and L2.
Note-
1. Let (L, ⋅, +, 0, 1) be a lattice L is said to complemented lattice if every element has atleast one complement.
2. A lattice (L, ⋅, +) is called a distributive lattice if for any a, b, c ∈L
a⋅ (b + c) = (a ⋅b) + (a ⋅c) and
a + (b ⋅c) = (a + b) ⋅ (a + c)
3. Let (L, ≤) be a lattice, with an upper bound 1. An element a ∈L is said to be meet irreducible if a = x ⋅y implies a = x or a = y.
If a ≠0 then a is meet irreducible if and only if a has unique immediate successor
A Boolean algebra is a distributive complemented lattice having at least two elements as well as 0 and 1.
A Boolean algebra is generally denoted by a 6-tuple, (B, +, ⋅, 1, 0, 1) where (B, +, ⋅) is a lattice with two binary operations + and ⋅, called the join and meet respectively is a unary operation in B. The elements 0 and 1 are the least and greatest elements of the lattice (B, +, ⋅). The following axioms are satisfied:
1. There exist at least two elements a, b in B and that a ≠b.
2. ∀a, b ∈B
(i) a+ b ∈B
(ii) a⋅b ∈B
3. For all a, b ∈B
(i) a+ b = b + a
(ii) a⋅b = b ⋅a
Commutative laws
4. Associative laws: for all a, b, c ∈B
(i) a+ (b + c) = (a + b) + c
(ii) a⋅(b ⋅c) = (a ⋅b) ⋅c
5. Distributive laws: for all a, b, c ∈B
(i) a+ (b ⋅c) = (a + b) ⋅(a + c)
(ii) a⋅(b + c) = (a ⋅b) + (a ⋅c)
6. (i) Existence of zero: There exists of B such that
a + 0 = a ∀a ∈B
The element 0 is called the zero element
(ii) Existence of unit: There exists 1 ∈B sum that
a⋅1 = a ∀a ∈B
The element 1 is called the unit element.
7. Existence of complement: ∀a ∈B there exists an element a′∈B such that
(i) a+ a′ = 1 and (ii) a ⋅a′ = 0
Sub-Boolean algebra-
Let (B, +, ⋅, ', 0, 1) be a Boolean algebra and S ≤B. If S contains the elements 0 and 1 and is closed under the operations +, and ⋅, then (S, +, ⋅, ', 0, 1) is called a sub-Boolean algebra.
Boolean functions
Let (B, +, ⋅, ', 0, 1) be a Boolean algebra. A function: f: 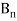 →B which is associated with a Boolean expression in n variables is called a Boolean function.
→B which is associated with a Boolean expression in n variables is called a Boolean function.
Boolean expression-
A Boolean expression or form, in n variables: 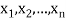 is any finite string of symbols formed as given below:
is any finite string of symbols formed as given below:
1. 0 and 1 are Boolean expression.
2. 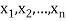 are Boolean expressions.
are Boolean expressions.
3. If αand βare Boolean expression, then (α)(β) and (α)+(β) are also Boolean expressions.
4. If α is a Boolean expression then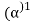 is also a Boolean expression.
is also a Boolean expression.
5. No strings symbols except those formed in accordance with the above rules are Boolean expressions.
Equivalent Boolean expression-
Two Boolean expression α(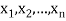 ) and β(
) and β(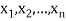 ) are said to be equivalent if one can be obtained from the other by a finite number of application of the identities of Boolean algebra.
) are said to be equivalent if one can be obtained from the other by a finite number of application of the identities of Boolean algebra.
Fundamental product-
A literal or a product of two or more literals in which no two literals involve the same variable is called a fundamental product.
Minterm-
A Boolean expression generated by 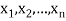 over B, which has the form of conjunction (product) of n literals is called a minterm.
over B, which has the form of conjunction (product) of n literals is called a minterm.
Minimization of Boolean expressions-
Algebra method-
Example: Simplify z (y+z) ((x + y + z).
Sol.
z(y + z) (x + y + z)
= (z y + z z) (x + y + z)
= (z y + z) (x + y + z)
= z (y + 1) (x + y + z)
= z (x + y + z)
= z x + z y + z z
= z x + z y + z
= z (x + y + 1)
= z (x + 1)
= z
Example: Simplify Y = (P + Q) (P + Q′) (P′+ Q)
Sol.
Y = (P + Q) (P + Q′) (P′+ Q)
= (P P+ P Q′+ P Q + Q Q′) (P′+ Q)
= (P + P Q′+ P Q + 0) (P′+ Q)
= (P + P Q′+ P Q) (P′+ Q)
= P P1 + P Q + P Q′P′+ P Q′Q + P Q P′+ P Q Q
= 0 + P Q + 0 + 0 + 0 + P Q
= P Q + P Q
= P Q
Example: Minimize the expression 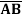 +
+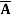 + A B
+ A B
Sol.
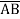 +
+ 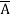 + A B
+ A B
= 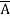 +
+ 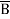 +
+ 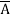 + A B
+ A B
= 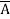 +
+ 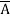 +
+ 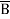 + A B
+ A B
= 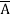 +
+ 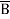 + A B
+ A B
= 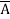 + A B +
+ A B + 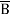
= (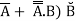
= 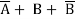
= 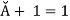
Hence
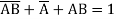
References:
1. Discrete Mathematics and its Applications, Kenneth H. Rosen, 7th Edition, McGraw Hill Education (India) Private Limited.
2. Discrete Mathematics D.S. Malik & K. K. Sen, Revised Edition Cengage Learning.
3. Elements of Discrete Mathematics, C.L. Liu and D.P. Mohapatra, 4th Edition, McGraw Hill Education (India) Private Limited.
4. Discrete Mathematics with Applications, Thomas Koshy, Elsevier.
5. Discrete and Combinatorial Mathematics, R. P. Grimaldi, Pearson.