Unit - 5
Magnetostatics
The Biot Savart Law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current. Biot–Savart law is consistent with both Ampere’s circuital law and Gauss’s theorem. The Biot-Savart law is fundamental to magnetostatics, playing a role similar to that of Coulomb’s law in electrostatics.
The Biot-Savart law can be stated as:
 ……….(1)
……….(1)
Where, k is a constant, depending upon the magnetic properties of the medium and system of the units employed.
In the SI system of unit,
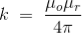 ……….(2)
……….(2)
Therefore, the final Biot-Savart law derivation is,
 ……….(3)
……….(3)
DERIVATION
Let us consider a long wire carrying a current I and also consider a point p in the space. The wire is presented in the picture below, by red colour.
Let us also consider an infinitely small length of the wire dl at a distance r from the point P as shown. Here, r is a distance-vector which makes an angle θ with the direction of current in the infinitesimal portion of the wire.
If you try to visualize the condition, you can easily understand the magnetic field density at point P due to that infinitesimal length dl of the wire is directly proportional to current carried by this portion of the wire.
As the current through that infinitesimal length of wire is the same as the current carried by the whole wire itself, we can write,
 ……….(4)
……….(4)
The magnetic field density at that point P due to that infinitesimal length dl of wire is inversely proportional to the square of the straight distance from point P to the center of dl. Mathematically we can write this as,
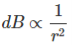 ……….(5)
……….(5)
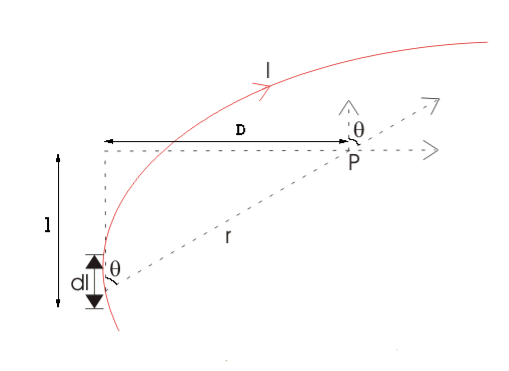
Figure 1
As θ be the angle between distance vector r and direction of current through this infinitesimal portion of the wire, the component of dl directly facing perpendicular to the point P is dlsinθ,
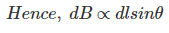 ……….(6)
……….(6)
Now, combining these three statements, we can write,
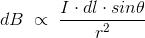 ……….(7)
……….(7)
This is the basic form of Biot Savart’ s Law
Now, putting the value of constant k (which we have already introduced at the beginning of this article) in the above expression, we get
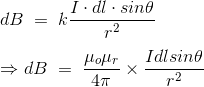 ……….(8)
……….(8)
Here, μ0 used in the expression of constant k is absolute permeability of air or vacuum and its value is 4π 10-7 Wb/ A-m in the SI system of units. μr of the expression of constant k is the relative permeability of the medium.
10-7 Wb/ A-m in the SI system of units. μr of the expression of constant k is the relative permeability of the medium.
Now, flux density(B) at the point P due to the total length of the current-carrying conductor or wire can be represented as,
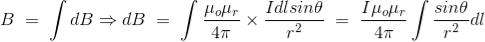 ……….(9)
……….(9)
If D is the perpendicular distance of the point P from the wire, then
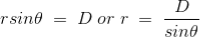 ……….(10)
……….(10)
Now, the expression of flux density B at point P can be rewritten as,
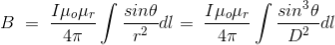
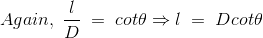 ……….(11)
……….(11)
As per the figure above,
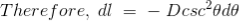 ……….(12)
……….(12)
Finally, the expression of B comes as,
 ……….(13)
……….(13)
This angle θ depends upon the length of the wire and the position of the point P. Say for a certain limited length of the wire, angle θ as indicated in the figure above varies from θ1 to θ2. Hence, magnetic flux density at point P due to the total length of the conductor is,
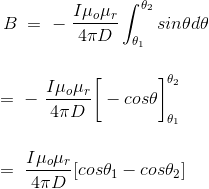 ……….(14)
……….(14)
Let’s imagine the wire is infinitely long, then θ will vary from 0 to π that is θ1 = 0 to θ2 = π. Putting these two values in the above final expression of Biot Savart law, we get,
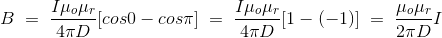 ……….(15)
……….(15)
This is nothing but the expression of Ampere’s Law.
Applications of Biot-Savart’s law
- This law can be used for calculating magnetic reactions even on the level of molecular or atomic.
- It can be used in the theory of aerodynamic for determining the velocity encouraged with vortex lines.
Consider a Rowland ring having a toroidal winding of winding of N turns around it. When a current i0 is sent through the winding, the ring is magnetized along its circumferential length. The current i0 is the real current which magnetizes the ring.
This magnetization arises due to the alignment of the elementary current-loops (magnetic dipoles) resulting from electronic motions in the materials. The small circles represent the current-loops. These internal tiny circular electron currents tend to cancel each other due to the fact that adjacent current are in opposite directions. As such there is no net current in the outer portions of the outer-most loops remain uncancelled. The numerous tiny localized surface currents can be replaced by a single closed current i5 along the surface. Such a current is called Amperian current.
Let A = area of cross and section and l = circumferential length of the ring. Then, volume of the ring = IA.
The ring behaves like a large dipole of magnetic movements is A.
Magnetization = M = magnetic moment per unit volume = iNA/lA = iN/l.
The magnetization M, therefore is the surface current per unit lengths of the ring. This is commonly called magnetization currents.
Now, the magnetic induction B with in material of the ring arises due to the free current i0 in the winding, as well as due to the magnetization of the ring itself which can be described in terms of Amperian surface current.
. : = B = μ0 (Ni0/l + iS/L) = μ0 (Ni0 /l +M) (.: is/L = M)
Here Ni0/l is the free current per unit and is/l is the Amperian surface current per unit length
. : B/ μ0 – M = Ni0 /l … (1)
The quantity B/ μ0 – M is called magnetizing field or magnetic field intensity H. i.e., H = B/μ0 – M
Or B = μ0 (H + M) … (2)
This is relation between the tree vectors B H and M points in the same direction as that of B or M and M. H points in the same direction as that of B or M. Its unit is Am-1
Eq. (1) can be written as H = Ni0/l = ni0
Where n is the number of turns per unit length. Thus the value of H depends only on the free current and is independent of the core material.
When no magnetic material is present in the core of the Rowland ring. i.e., there is vacuum in the core, M = 0. Therefore, Eq (2) becomes
B0 = μ0 H … (3)
In vacuum, the magnetic field strength H is related to the magnetic induction B0 by the above relation.
When a magnetic material is placed in an external magnetic field, the specimen is magnetized by producing (or reorienting) magnetic dipoles in the specimen. This will produce additional field. Thus the resultant field B is greater than B0. In such a case, H is related to B by the relation,
H = (B/μ0) – M.
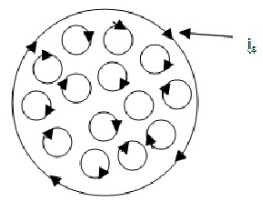
Figure: 2
In homogeneous media, electromagnetic quantities vary smoothly and continuously. At a boundary between dissimilar media, however, it is possible for electromagnetic quantities to be discontinuous. Continuities and discontinuities in fields can be described mathematically by boundary conditions and used to constrain solutions for fields away from these boundaries. In this section, we derive boundary conditions on the magnetic field intensity H.
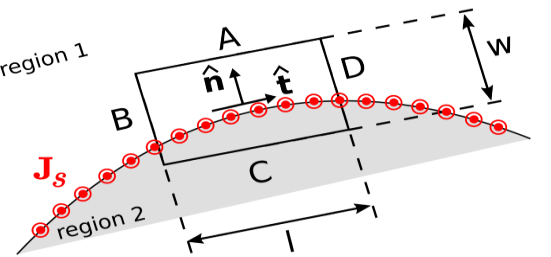
Figure 3: Determining the boundary condition on H at the smooth boundary between two material regions.
To begin, consider a region consisting of only two media that meet at a smooth boundary as shown in above Figure. The desired boundary condition can be obtained directly from Ampere’s Circuital Law
∮C H⋅dl= Iencl ……….(1)
Where C is any closed path and Iencl is the current that flows through the surface bounded by that path in the direction specified by the “right-hand rule” of Stokes’ theorem.
Let C take the form of a rectangle centered on a point on the boundary as shown in Figure, perpendicular to the direction of current flow at that location.
Let the sides A, B, C, and D be perpendicular and parallel to the boundary. Let the length of the parallel sides be l, and let the length of the perpendicular sides be w.
Now we apply Ampere’s Circuital Law, We must integrate in a counter-clockwise direction in order to be consistent with the indicated reference direction for Js
Thus:
∮H⋅dl=∫A H⋅dl+∫B H⋅dl+∫C H⋅dl+∫D H⋅dl=Iencl
Now we let w and l become vanishingly small while maintaining the ratio l/w and keeping C centered on the boundary. In this process, the contributions from the B and D segments become equal in magnitude but opposite in sign; i.e.,
∫B H⋅dl +∫D H⋅dl →0 ………(2)
This leaves
∫A H⋅dl+∫C H⋅dl=Iencl
Let us define the unit vector 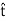 (“tangent”) as shown in Figure 8. Now we have simply:
(“tangent”) as shown in Figure 8. Now we have simply:
H1⋅(−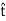 Δl)+H2⋅(+
Δl)+H2⋅(+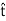 Δl)=Iencl ………(3)
Δl)=Iencl ………(3)
Where H1 and H2 are the fields evaluated on the two sides of the boundary, and Δl→0 is the length of sides A and C. As always, Iencl (units of A) may be interpreted as the flux of the current density Js (units of A/m) flowing past a line on the surface having length Δl (units of m) perpendicular to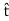
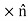 , where
, where 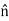 is the normal to the surface, pointing into Region 1. Stated mathematically:
is the normal to the surface, pointing into Region 1. Stated mathematically:
Iencl →Js ⋅(Δl 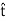
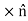 ) ………(4)
) ………(4)
Before proceeding, note this is true regardless of the particular direction we selected for 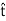 ; it is only necessary that
; it is only necessary that 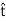 be tangent to the boundary. Thus,
be tangent to the boundary. Thus, 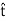
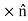 need not necessarily be in the same direction as Js. Now Equation (3) can be written:
need not necessarily be in the same direction as Js. Now Equation (3) can be written:
H1⋅(−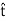 Δl)+H2⋅(+
Δl)+H2⋅(+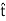 Δl)=Js ⋅(Δl
Δl)=Js ⋅(Δl 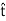
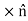 ) ………(5)
) ………(5)
Eliminating the common factor of Δl and arranging terms on the left:
(H2−H1)⋅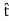 = Js ⋅(
= Js ⋅(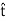
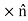 ) ………(6)
) ………(6)
The right side may be transformed using a vector identity (A⋅(B×C)=B⋅(C×A)=C⋅(A×B) to obtain:
(H2−H1)⋅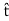 =
= 
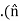
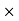 Js) ………(7)
Js) ………(7)
Equation (7) is the boundary condition we seek. We have found that the component of (H2−H1) (the difference between the magnetic field intensities at the boundary) in any direction tangent to the boundary is equal to the component of the current density flowing in the perpendicular direction 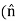
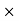 Js).
Js).
A discontinuity in the tangential component of the magnetic field intensity at the boundary must be supported by surface current flowing in a direction perpendicular to this component of the field.
An important consequence is that If there is no surface current, then the tangential component of the magnetic field intensity is continuous across the boundary.
It is possible to obtain a mathematical form of the boundary condition that is more concise and often more useful than Equation (7).
This form may be obtained as follows. First, we note that the dot product with respect to 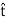 ton both sides of Equation (7) means simply “any component that is tangent to the boundary.” We need merely to make sure we are comparing the same tangential component on each side of the equation.
ton both sides of Equation (7) means simply “any component that is tangent to the boundary.” We need merely to make sure we are comparing the same tangential component on each side of the equation.
For example 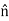 ×(H2−H1) is tangential to the boundary, since
×(H2−H1) is tangential to the boundary, since 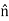 is perpendicular to the boundary and therefore any cross product involving
is perpendicular to the boundary and therefore any cross product involving  will be perpendicular to
will be perpendicular to 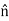 . The corresponding component of the current density is
. The corresponding component of the current density is 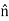 ×(
×(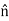 ×Js),
×Js),
So Equation (7) may be equivalently written as follows:
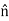 ×(H2−H1)=
×(H2−H1)= 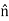 ×(
×( ×Js) ………(8)
×Js) ………(8)
Applying a vector identity (A×(B×C)=B(A⋅C)−C(A⋅B) to the right side of Equation (8) we obtain:
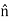 ×
×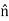 ×Js=
×Js= 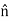 (
(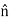 .Js) - Js
.Js) - Js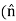 .
.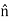 ) =
) =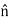 (0)-
(0)-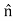 (1)Js = - Js
(1)Js = - Js
Therefore:
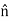 × (H2−H1) = - Js …………(9)
× (H2−H1) = - Js …………(9)
The minus sign on the right can be eliminated by swapping H2 and H1 on the left, yielding
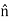 × (H1−H2) = - Js ………...(10)
× (H1−H2) = - Js ………...(10)
This is the form in which the boundary condition is most commonly expressed.
It is worth noting what this means for the magnetic field intensity B. Since B=μH
In the absence of surface current, the tangential component of B across the boundary between two material regions is discontinuous if the permeabilities are unequal.
Key Takeaways
- In homogeneous media, electromagnetic quantities vary smoothly and continuously.
- At a boundary between dissimilar media, however, it is possible for electromagnetic quantities to be discontinuous.
- Continuities and discontinuities in fields can be described mathematically by boundary conditions and used to constrain solutions for fields away from these boundaries.
- (H2−H1)⋅
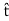 =
= 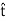

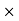 Js) is the boundary condition
Js) is the boundary condition - In the absence of surface current, the tangential component of B across the boundary between two material regions is discontinuous if the permeabilities are unequal.
The magnetic effects in magnetic materials are due to atomic magnetic dipoles in the materials. These dipoles result from effective current loops of electrons in atomic orbits, from effects of electron spin & from the magnetic moments of atomic nuclei.
The electric currents in an atom are caused by orbital and spin motions of electrons and those of its nucleus. Since all these motions of charged particles form closed electric currents, they are equivalent to “magnetic dipoles”. When such dipoles are subjected to an external electric field, they experience a torque which tends to align their magnetic moments in the direction of the externally applied field.
SOME IMPORTANT DEFINITIONS
Magnetic dipole
Each tiny dimension of a magnetic material (or) atoms in magnetic materials is called magnetic dipole. This magnetic dipole produces magnetic moment depending on the alignment with respect to the applied magnetic field.
Magnetic flux (Ф)
It is defined as the amount of magnetic lines of forces passing perpendicularly through unit area of a given material. It is denoted by ‘Ф’
Ф=AB
Where A= Area of cross section of the material in m2
B = magnetic Induction in Wb/ m2
Units: Weber (Wb)
Intensity of Magnetization (M)
When a material is magnetized, it develops a net magnetic moment. The magnetic moment per unit volume is called Intensity of magnetization.
Magnetization (M) = 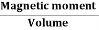
Units: Amp/m
Magnetic Induction (B)
Magnetic induction at a point is defined as the force experienced by a unit North Pole Placed at that point. It is denoted by ‘B’i.e.
B =
Unit is weber / m2
Magnetizing field strength (H)
When a medium is exposed to a magnetic field of intensity ‘H’, it causes an induction ‘B’ in the medium.i.e. B H
B = μH
Where μ = absolute permeability of the medium. If the medium is air or vacuum B=μ0H
μ0=permeability of free space i.e. air or vacuum
μ0=4𝜋×10-7 H/m
Units for H: Amp /m
Permeability (μ)
It indicates with which the material allows magnetic lines of force to pass through it.
Or
It is the ability of the medium to pass magnetic lines of forces through it.
There are three Permeabilities i.e. μ1,μ0, μr
μ = μ0μr
Where μ = Absolute permeability of the medium
μ0 = Permeability of free space i.e. air or vacuum
μr = Relative permeability of the medium
Magnetic moment
Magnetic moment μm = (current) × (area of circulating orbit)
μm = (I) × (𝜋r2)
Units: Amp-m2
When the magnetic dipoles (atoms consisting of charged particles like protons & neutrons) undergo orbital motion (or) spin motion produces a magnetic moment. Since motion of charged particles is considered as closed electric current loops which in turn produces a magnetic moment.
Magnetic susceptibility (χ)
If H is the applied magnetizing field intensity and M is the amount of magnetization of the material,
Then χ = 
χ = 0 in vacuum
χ = +ve for paramagnetic and Ferro magnetic materials
χ = -ve for diamagnetic materials
Units: It has no units.
CLASSIFICATION OF MAGNETIC MATERIALS
Magnetic materials are classified as follows:
- Diamagnetic
- Paramagnetic
- Ferro magnetic
- Anti-Ferro magnetic
- Ferric magnetic or ferrites
DIAMAGNETIC
The orbital motion of electrons around the nucleus produces a magnetic field perpendicular to the plane of the orbit. Thus each electron orbit has finite orbital magnetic dipole moment. Since the orbital planes are oriented in random manner, the vector sum of magnetic moments is zero and there is no resultant magnetic moment for each atom.
In the presence of an external magnetic field, some electrons are speeded up and some are slowed down. The electrons whose moments were anti-parallel are speeded up according to Lenz’s law and this produces an induced magnetic moment in a direction opposite to the field. The induced moment disappears as soon as the external field is removed.
When placed in a non-uniform magnetic field, the interaction between induced magnetic moment and the external field creates a force which tends to move the material from stronger part to weaker part of the external field. It means that diamagnetic material is repelled by the field.
This action is called diamagnetic action and such materials are known as diamagnetic materials. Examples: Bismuth, Copper and Water etc.
Diamagnetism is a fundamental property of all matter, although it is usually very weak. It is due to the non-cooperative behaviour of orbiting electrons when exposed to an applied magnetic field. Diamagnetic substances are composed of atoms which have no net magnetic moments (ie., all the orbital shells are filled and there are no unpaired electrons). However, when exposed to a field, a negative magnetization is produced and thus the susceptibility is negative. If we plot M vs H, we see
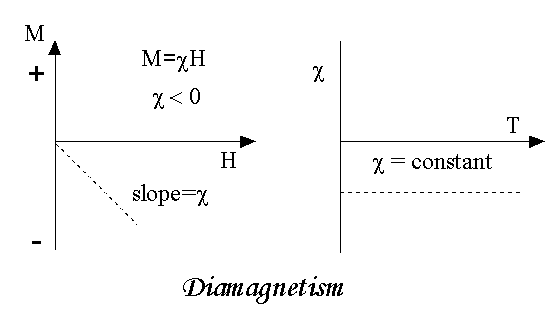
Figure 4
Note that when the field is zero the magnetization is zero. The other characteristic behaviour of diamagnetic materials is that the susceptibility is temperature independent. Some well-known diamagnetic substances, in units of 10-8 m3/kg, include:
Quartz (SiO2) -0.62
Calcite (CaCO3) -0.48
Water -0.90
The properties of diamagnetic materials are
- Magnetic susceptibility is negative.
- Relative permeability is slightly less than unity.
- The magnetic field lines are repelled or expelled by diamagnetic materials when placed in a magnetic field.
- Susceptibility is nearly temperature independent.
- Examples: Cu, Au, Zn, H20, Bi etc. organic materials
PARAMAGNETIC MATERIALS
In some magnetic materials, each atom or molecule has net magnetic dipole moment which is the vector sum of orbital and spin magnetic moments of electrons. Due to the random orientation of these magnetic moments, the net magnetic moment of the materials is zero.
In the presence of an external magnetic field, the torque acting on the atomic dipoles will align them in the field direction. As a result, there is net magnetic dipole moment induced in the direction of the applied field. The induced dipole moment is present as long as the external field exists.
As we come to know this class of materials, some of the atoms or ions in the material have a net magnetic moment due to unpaired electrons in partially filled orbitals. One of the most important atoms with unpaired electrons is iron. However, the individual magnetic moments do not interact magnetically, and like diamagnetism, the magnetization is zero when the field is removed. In the presence of a field, there is now a partial alignment of the atomic magnetic moments in the direction of the field, resulting in a net positive magnetization and positive susceptibility.
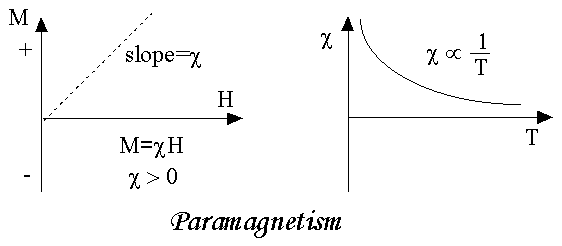
Figure 5
In addition, the efficiency of the field in aligning the moments is opposed by the randomizing effects of temperature. This results in a temperature dependent susceptibility, known as the Curie Law.
At normal temperatures and in moderate fields, the paramagnetic susceptibility is small (but larger than the diamagnetic contribution). Unless the temperature is very low (<<100 K) or the field is very high paramagnetic susceptibility is independent of the applied field. Under these conditions, paramagnetic susceptibility is proportional to the total iron content. Many iron bearing minerals are paramagnetic at room temperature. Some examples, in units of 10-8 m3/kg, include:
Montmorillonite (clay) 13
Nontronite (Fe-rich clay) 65
Biotite (silicate) 79
Siderite (carbonate) 100
Pyrite (sulphide) 30
The paramagnetism of the matrix minerals in natural samples can be significant if the concentration of magnetite is very small. In this case, a paramagnetic correction may be needed.
The properties of paramagnetic materials are:
- Magnetic susceptibility is positive and small.
- Relative permeability is greater than unity.
- The magnetic field lines are attracted into the paramagnetic materials when placed in a magnetic field.
- Susceptibility is inversely proportional to temperature.
FERROMAGNETIC MATERIALS
An atom or a molecule in a ferromagnetic material possesses net magnetic dipole moment as in a paramagnetic material. A ferromagnetic material is made up of smaller regions, called ferromagnetic domain (Figure 3.27). Within each domain, the magnetic moments are spontaneously aligned in a direction. This alignment is caused by strong interaction arising from electron spin which depends on the inter-atomic distance. Each domain has net magnetisation in a direction. However the direction of magnetisation varies from domain to domain and thus net magnetisation of the specimen is zero.
In the presence of external magnetic field, two processes take place
1. the domains having magnetic moments parallel to the field grow in size
2. the other domains (not parallel to field) are rotated so that they are aligned with the field.
As a result of these mechanisms, there is a strong net magnetisation of the material in the direction of the applied field
When placed in a non-uniform magnetic field, the ferromagnetic materials will have a strong tendency to move from weaker to stronger part of the field. Materials which exhibit strong magnetism in the direction of applied field are called ferromagnetic materials.
When you think of magnetic materials, you probably think of iron, nickel or magnetite. Unlike paramagnetic materials, the atomic moments in these materials exhibit very strong interactions. These interactions are produced by electronic exchange forces and result in a parallel or antiparallel alignment of atomic moments. Exchange forces are very large, equivalent to a field on the order of 1000 Tesla, or approximately a 100 million times the strength of the earth's field.
The exchange force is a quantum mechanical phenomenon due to the relative orientation of the spins of two electrons.
Ferromagnetic materials exhibit parallel alignment of moments resulting in large net magnetization even in the absence of a magnetic field.
The elements Fe, Ni, and Co and many of their alloys are typical ferromagnetic materials.
Two distinct characteristics of ferromagnetic materials are their
(1) Spontaneous magnetization and
(2) Magnetic ordering temperature
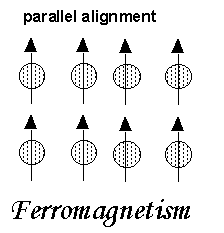
Figure 6
Spontaneous Magnetization
The spontaneous magnetization is the net magnetization that exists inside a uniformly magnetized microscopic volume in the absence of a field. The magnitude of this magnetization, at 0 K, is dependent on the spin magnetic moments of electrons.
A related term is the saturation magnetization which we can measure in the laboratory. The saturation magnetization is the maximum induced magnetic moment that can be obtained in a magnetic field (Hsat); beyond this field no further increase in magnetization occurs.
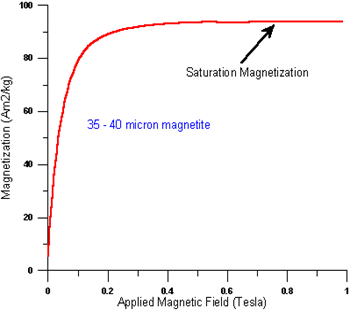
Figure 7
The difference between spontaneous magnetization and the saturation magnetization has to do with magnetic
Domains (more about domains later). Saturation magnetization is an intrinsic property, independent of particle size but dependent on temperature.
There is a big difference between paramagnetic and ferromagnetic susceptibility. As compared to paramagnetic materials, the magnetization in ferromagnetic materials is saturated in moderate magnetic fields and at high (room-temperature) temperatures:
| Hsat Tesla | T range (K) | χ 10-8m3/kg |
Paramagnets | >10 | <<100 | ~50 |
Ferromagnets | ~1 | ~300 | 1000-10000 |
The properties of ferromagnetic materials are:
- Magnetic susceptibility is positive and large.
- Relative permeability is large.
- The magnetic field lines are strongly attracted into the ferromagnetic materials when placed in a magnetic field.
- Susceptibility is inversely proportional to temperature.
A hysteresis loop (also known as a hysteresis curve) is a four-quadrant graph that shows the relationship between the induced magnetic flux density B and the magnetizing force H. It is often referred to as the B-H loop. From hysteresis loops, we can determine a number of magnetic properties about a material. Such as the retentivity, residual magnetism (or residual flux), coercive force, permeability, and the reluctance.
To understand a hysteresis loop, let’s suppose we take a magnetic material to use as a core around which insulated wire is wound.
The coils are connected to a DC supply through a variable resistor to vary the current “I”. We know that current I is directly proportional to the value of magnetizing force (H) as
Where N = number of turns of coil and l is the effective length of the coil. The magnetic flux density of this core is B which is directly proportional to magnetizing force H.
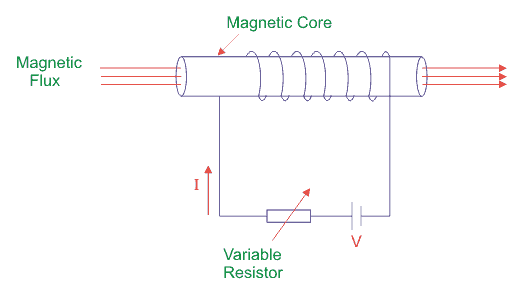
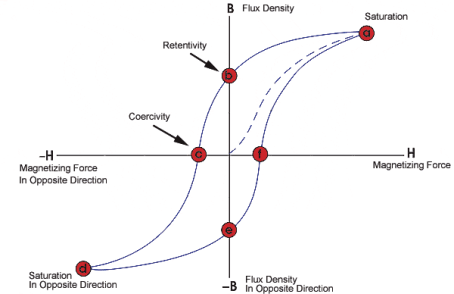
Figure 8: Hysteresis loop
Application:
i) Permanent magnets:
The materials with high retentivity, high coercivity and high permeability are suitable for making permanent magnets. Examples: Steel and Alnico
Ii) Electromagnets:
The materials with high initial permeability, low retentivity, low coercivity and thin hysteresis loop with smaller area are preferred to make electromagnets.
Examples: Soft iron and Mu metal (Nickel Iron alloy).
Iii) Core of the transformer:
The materials with high initial permeability, large magnetic induction and thin hysteresis loop with smaller area are needed to design transformer cores.
Examples: Soft iron
References:
1. Fundamentals of Physics Electricity and Magnetism, Halliday and Resnick, tenth edition (published 2013).
2. Electricity, magnetism and light, W. Saslow, 1st edition
3. Electromagnetic Theory, Singh and Prasad, I. K. International Publication, 1/e
4. Electricity, Magnetism & Electromagnetic Theory, S. Mahajan and Choudhury, 2012, Tata McGraw
5. Elements of Electromagnetics, M.N.O. Sadiku, 2010, Oxford University Press.