Unit - 3
Vector Calculus
A scalar field is an assignment of a scalar to each point in region in the space. E.g. The temperature at a point on the earth is a scalar field.
A vector field is an assignment of a vector to each point in a region in the space. e.g. The velocity field of a moving fluid is a vector field as it associates a velocity vector to each point in the fluid.
One of the values of calculating the scalar electric potential (voltage) is that the electric field can be calculated from it. The component of electric field in any direction is the negative of rate of change of the potential in that direction.
If the differential voltage change is calculated along a direction ds, then it is seen to be equal to the electric field component in that direction times the distance ds.

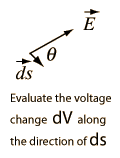
The electric field can then be expressed as
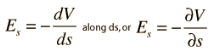
This is called a partial derivative.
For rectangular coordinates, the components of the electric field are
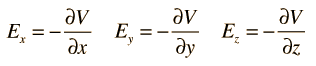
Express as a gradient.
The expression of electric field in terms of voltage can be expressed in the vector form

This collection of partial derivatives is called the gradient, and is represented by the symbol ∇. The electric field can then be written
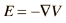
Expressions of the gradient in other coordinate systems are often convenient for taking advantage of the symmetry of a given physical problem.
One approach to continuous charge distributions is to define electric flux and make use of Gauss' law to relate the electric field at a surface to the total charge enclosed within the surface. This involves integration of the flux over the surface.
Another approach is to relate derivatives of the electric field to the charge density. This approach can be considered to arise from one of Maxwell's equations and involves the vector calculus operation called the divergence. The divergence of the electric field at a point in space is equal to the charge density divided by the permittivity of space.

In a charge-free region of space where r = 0, we can say
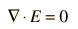
While these relationships could be used to calculate the electric field produced by a given charge distribution, the fact that E is a vector quantity increases the complexity of that calculation. It is often more practical to convert this relationship into one which relates the scalar electric potential to the charge density. This gives Poisson's equation and Laplace’s equation.
The curl of a vector field E = E (x, y, z) is defined, in terms of the del operators ∇, like a cross product
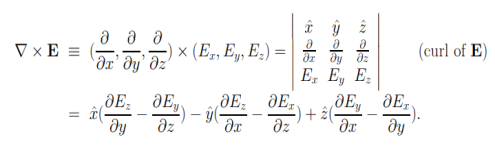
The proof of curl-free nature of static electric fields can be given by first showing that Coulomb field of a static charge is curl-free, and then making use of the superposition principle along with the fact that the curl of a sum must be the sum of curls — like differentiation, “taking curl” is a linear operation
t ∇ × E = 0
With the Coulomb field of a point charge Q located at the origin.
If V is the volume bounded by a closed surface S and  is a vector point function with continuous derivative-
is a vector point function with continuous derivative-
Then it can be written as-
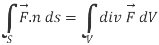
Where unit vector to the surface S.
unit vector to the surface S.
Example-1: Prove the following by using Gauss divergence theorem-
1. 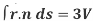
2. 
Where S is any closed surface having volume V and 
Sol. Here we have by Gauss divergence theorem-

Where V is the volume enclose by the surface S.
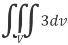
We know that-

= 3V
2.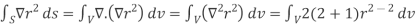
Because 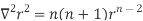

Example – 2 Show that 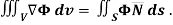
Sol
By divergence theorem,  ..…(1)
..…(1)
Comparing this with the given problem let 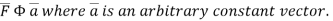
Hence, by (1)
 ………….(2)
………….(2)
Now ,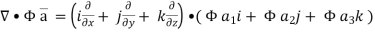
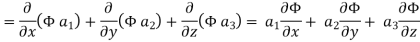
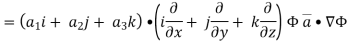
Hence, from (2), We get,
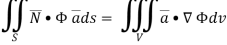
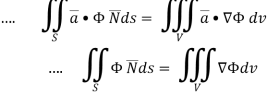
Example Based on Gauss Divergence Theorem
- Show that

Soln. We have Gauss Divergence Theorem
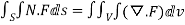
By data, F=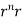
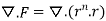

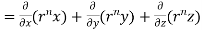

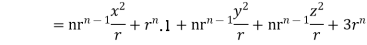
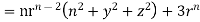
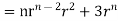
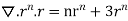
=(n+3)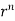
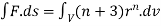
2 Prove that 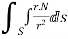 =
=
Soln. By Gauss Divergence Theorem,
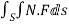 =
=
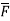 =
=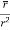 =
=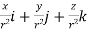
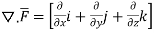 .[
.[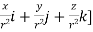
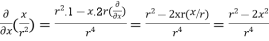
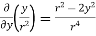
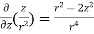
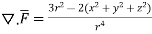 =
= 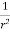
Stokes Theorem (also known as Generalized Stoke’s Theorem) is a declaration about the integration of differential forms on manifolds, which both generalizes and simplifies several theorems from vector calculus. As per this theorem, a line integral is related to a surface integral of vector fields.
The Stoke’s theorem states that “the surface integral of the curl of a function over a surface bounded by a closed surface is equal to the line integral of the particular vector function around that surface.”
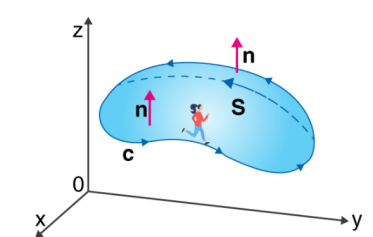
∮CF⃗.dr→=∬S (▽×F⃗).dS→
Where,
C = A closed curve.
S = Any surface bounded by C.
F = A vector field whose components have continuous derivatives in an open region of R3 containing S.
This classical declaration, along with the classical divergence theorem, fundamental theorem of calculus, and Green’s theorem are exceptional cases of the general formulation specified above.

If you walk in the positive direction around C with your head pointing in the direction of n, the surface will always be on your left.
S is an oriented smooth surface bounded by a simple, closed smooth-boundary curve C with positive orientation.
References:
1. Fundamentals of Physics Electricity and Magnetism, Halliday and Resnick, tenth edition (published 2013).
2. Electricity, magnetism and light, W. Saslow, 1st edition
3. Electromagnetic Theory, Singh and Prasad, I. K. International Publication, 1/e
4. Electricity, Magnetism & Electromagnetic Theory, S. Mahajan and Choudhury, 2012, Tata McGraw
5. Elements of Electromagnetics, M.N.O. Sadiku, 2010, Oxford University Press