UNIT 1
Introduction of Engineering Drawing
Engineering drawing is a two-dimensional representation of three dimensional objects. In general, it provides necessary information about the shape, size, surface quality, material, manufacturing process, etc., of the object. It is the graphic language from which a trained person can visualize objects.
Drawings prepared in one country may be utilised in any other country irrespective of the language spoken. Hence, engineering drawing is called the universal language of engineers. Any language to be communicative, should follow certain rules so that it conveys the same meaning to everyone. Similarly, drawing practice must follow certain rules, if it is to serve as a means of communication. For this purpose, Bureau of Indian Standards (BIS) adapted the International Standards on code of practice for drawing. The other foreign standards are: DIN of Germany, BS of Britain and ANSI of America.
Role of Engineering Drawing
The ability to read drawing is the most important requirement of all technical people in any profession. As compared to verbal or written description, this method is brief and clearer. Some of the applications are: building drawing for civil engineers, machine drawing for mechanical engineers, circuit diagrams for electrical and electronics engineers, computer graphics for one and all.
The subject in general is designed to impart the following skills.
1. Ability to read and prepare engineering drawings.
2. Ability to make free - hand sketching of objects.
3. Power to imagine, analyze and communicate, and
4. Capacity to understand other subjects.
Curves used in engineering practice:
The profile of number of objects consists of various types of curves.
1. Conic sections:
The section obtained by intersection of a right circular cone by a plane, in different positions relative to the axis of the cone are called conics.
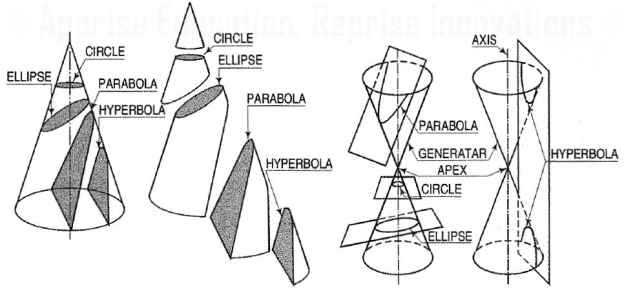
Conic sections are always "smooth". More precisely, they never contain any inflection points. This is important for many applications, such as aerodynamics, civil engineering, mechanical engineering, etc.
The conic may be defined as the locus of a point in a plane, wherein the ratio of its distance from a fixed point and a fixed straight line is always constant. The fixed point is called the focus and the fixed line, the directrix.
The ratio 
is called eccentricity and is denoted by ‘e’. It is always less the 1 for ellipse, equal to 1 for parabola and greater than 1 for hyperbola.
Use of elliptical curves is made in arches, bridges, dams, monuments, man holes, etc. Mathematically an ellipse can be described by equation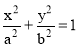
.
Here ‘a’ and ‘b’ are half the length of major and minor axes of ellipse and x and y are co-ordinates.
2.1 Parabola:
Use of parabolic curves is made in arches, bridges, sound reflectors, light reflectors, etc. Mathematically it can be described by an equation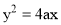 
or
.
Involute:
The involute is a curve traced out by an end of a piece of thread unwound from a circle or a polygon, the thread being kept tight. It may also be defined as a curve traced out by a point in a straight line which rolls without slipping along a circle or a polygon.
It is used as teeth profile of gear wheel.
Mathematically it can be described as by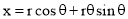 
, 
, where “r” is the radius of the circle.
Spiral:
If a line rotates in a plane about one of its ends and if at the same time, a point moves along the line continuously in one direction, the curve traced out by the moving point is called a spiral. The point about which the line rotates is called a pole.
The line joining any point on the curve with the pole is called the radius vector and the angle between this line and the line in its initial position is called the vectorial angle.
Archemedian spiral:
It is a curve traced out by a point moving in such a way that its movement towards and away from the pole is uniform with the increase of the vectorial angle from the starting line.
The use of this curve is made in teeth profiles of helical gears, profile of cams, etc.
Cycloid curves- only Cycloid
Cycloid is a curve generated by a point on the circumference of a circle which rolls along a straight line. It can be described by an equation,
y = a (1 - cosθ) or x = a (θ - sinθ)
To construct a cycloid, given the diameter of the generating circle.
(i) With centre C and given radius R, draw a circle. Let P be the generating point.
(ii) Draw a line PA tangential to and equal to the circumference of the circle.
(iii) Divide the circle and the line PA into the same number of equal parts, say 12,and mark the division-points as shown.
(iv) Through C, draw a line CB parallel and equal to PA.
(v) Draw perpendiculars at points 1, 2 etc. cutting CB at points C1, C2 etc.
Assume that the circle starts rolling to the right. When point 1' coincides with 1, centre C will move to C1. In this position of the circle, the generating point P will have moved to position P1 on the circle, at a distance equal to P'1 from point 1. It is evident that P1 lies on the horizontal line through 1' and at a distance R from C1. Similarly, P2 will lie on the horizontal line through 2' and at the distance R from C2.
Construction:
(vi)Through the points 1 ', 2' etc. draw lines parallel to PA.
(vii) With centres C1, C2 etc. and radius equal to R, radius of generating circle, draw arcs cutting the lines through 1 ', 2' etc. at points P1, P2 etc. respectively. Draw a smooth curve through points P, P1, P2 …. A. This curve is the required cycloid.
Normal and tangent to a cycloid curve: The rule for drawing a normal to all cycloidal curves:
The normal at any point on a cycloidal curve will pass through the corresponding point of contact between the generating circle and the directing line or circle. The tangent at any point is perpendicular to the normal at that point.
Involute:
The involute is a curve traced out by an end of a piece of thread unwound from a circle or a polygon, the thread being kept tight. It may also be defined as a curve traced out by a point in a straight line which rolls without slipping along a circle or a polygon. Involute of a circle is used as teeth profile of gear wheel. Mathematically it can be described by x = rcosθ + rθsinθ, y = rsinθ - rθcosθ, where "r" is the radius of a circle.
Problem: To draw an involute of a given circle.
With centre C, draw the given circle. Let P be the starting point, i.e. the end of the thread.
Suppose the thread to be partly unwound, say upto a point 1. P will move to a position P1 such that 1P1 is tangent to the circle and is equal to the arc 1 P. P1 will be a point on the involute.
Construction:
(i) Draw a line PQ, tangent to the circle and equal to the circumference of the circle.
(ii) Divide PQ and the circle into 12 equal parts.
(iii) Draw tangents at points 1, 2, 3 etc. and mark on them points P1, P2, P3 etc. such that 1P1 = P1', 2P2 = P2', 3P3 = P3' etc.
Draw the involute through the points P, P1, P2 .... Etc.
Normal and tangent to an involute:
The normal to an involute of a circle is tangent to that circle.
Problem:
To draw a normal and a tangent to the involute of a circle at a point N on it.
(i) Draw a line joining C with N.
(ii) With CN as diameter describe a semi-circle cutting the circle at M.
(iii) Draw a line through N and M. This line is the normal. Draw a line ST, perpendicular to NM and passing through N. ST is the tangent to the involute.
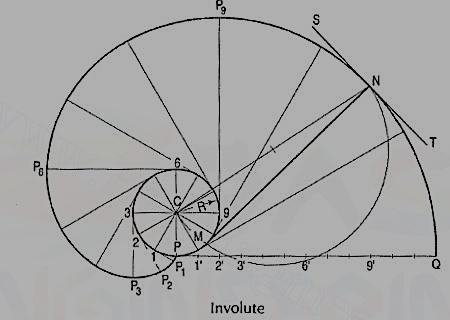
Problem: Trace the paths of the ends of a straight-line AP, 100 mm long, when it rolls, without slipping, on a semi-circle having its diameter AB, 75 mm long. (Assume the line AP to be tangent to the semi-circle in the starting position.)
(i) Draw the semi-circle and divide it into six equal parts.
(ii) Draw the line AP and mark points 1, 2 etc. such that A1 = arc A1 ', A2 = arc A2' etc. The last division SP will be of a shorter length. On the semi-circle, mark a point P' such that S'P' = SP.
(iii) At points 1 ', 2' etc. draw tangents and on them, mark points P1, P2 etc. such that 1' P1 = 1P, 2' P2 =2P .... And 5' P5 = 5' P6 =SP. Similarly, mark pointsA1, A2 etc. such that A11'= A1, A22' = A2 .... And A'p'= AP. Draw the required curves through points P,P1 .... And P', and through points A, A1 .... And A'.
If AP is an inelastic string with the end A attached to the semicircle, the end P will trace out the same curve PP' when the string is wound round the semi-circle.
Involute:
The involute is a curve traced out by an end of a piece of thread unwound from a circle or a polygon, the thread being kept tight. It may also be defined as a curve traced out by a point in a straight line which rolls without slipping along a circle or a polygon.
It is used as teeth profile of gear wheel.
Mathematically it can be described as by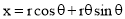 
, 
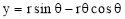, where “r” is the radius of the circle.
An involute is a curve traced by a point on a perfectly flexible string, while unwinding from around a circle or polygon the string being kept taut (tight). It is also a curve traced by a point on a straight line while the line is rolling around a circle or polygon without slipping.
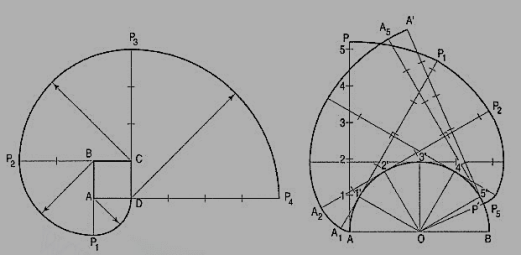
To draw an involute of a given square.
1. Draw the given square ABCD of side a.
2. Taking A as the starting point, with centre B and radius BA=a, draw an arc to intersect the
Line CB produced at Pl.
3. With Centre C and radius CP1 =2 a, draw on arc to intersect the line DC produced at P 2.
4. Similarly, locate the points P3 and P4.
The curve through A, P1, P2, P3 and P4 is the required involute.
A P4 is equal to the perimeter of the square.
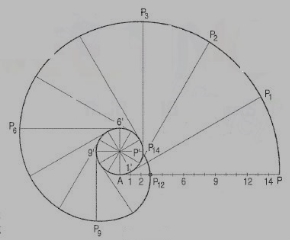
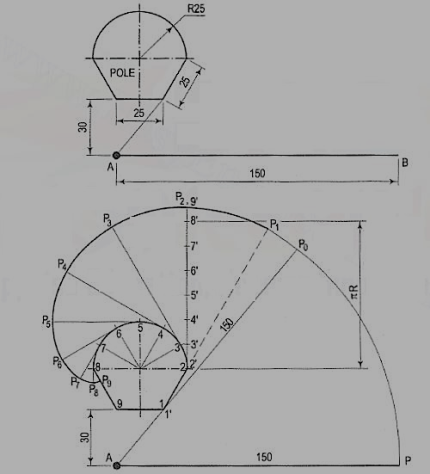
AP is a rope 1.50-metre-long, tied to peg at A as shown in fig. 24. Keeping it always tight, the rope is wound round the pole. Draw the curve traced out by the end P. Use scale 1 :20.
Draw given figure to the scale.
(ii) From A, draw a line passing through 1. A as centre and AP as radius, draw the arc intersecting extended line A1' at P0. Extend the side 1-2, 1 as centre and 1 'Po as radius, draw the arc to intersect extended line 1-2 at P1.
(iii) Divide the circumference of the semicircle into six equal parts and label it as 2, 3, 4, 5, 6, 7 and 8.
(iv) Draw a tangent to semicircle from 2 such that 2'-P1 = 2'-P2 . Mark 8' on this tangent such that 2'-8' = nR. Divide 2'-8' into six equal parts.
(v) Similarly draw tangents at 3, 4, 5, 6, 7 and 8 in anti-clockwise direction such that 3-P3 = 3'-9', 4-P4 = 4'-9', 5-P5 = 5'-9', 6-P6 = 6'-9', 7-P7 = 7'-9', 8-P8 = 8'-9' and 8-P9 = 8'-9' respectively.
(vi) Join P1, P2, ....• , P9 with smooth curve.
Spiral:
If a line rotates in a plane about one of its ends and if at the same time, a point moves along the line continuously in one direction, the curve traced out by the moving point is called a spiral. The point about which the line rotates is called a pole.
The line joining any point on the curve with the pole is called the radius vector and the angle between this line and the line in its initial position is called the vectorial angle.
Archimedean spiral:
It is a curve traced out by a point moving in such a way that it’s movement towards and away from the pole is uniform with the increase of the vectorial angle from the starting line.
The use of this curve is made in teeth profiles of helical gears, profile of cams, etc.
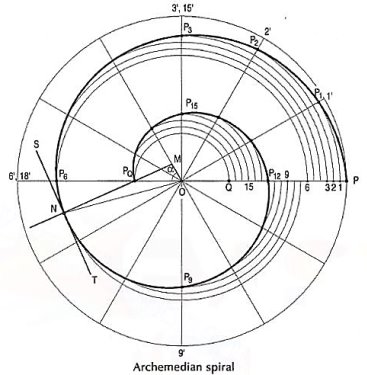
To construct an Archimedean spiral of 
convolutions given the greatest and the shortest radii.
Let O be the pole, OP the greatest radius and OQ the shortest radius.
(i) With centre O and radius equal to OP, draw a circle. OP revolves around0 for 
revolutions. During this period, P moves towards 0, the distance equal to (OP - OQ) i.e. QP.
(ii) Divide the angular movements of OP, viz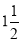 
revolutions i.e. 540°and the line QP into the same number of equal parts, say 18 (one revolution divided into 12 equal parts).
When the line OP moves through one division, i.e. 30°, the point P will move towards O by a distance equal to one division of QP to a point P1.
(iii) To obtain points systematically draw arcs with centre O and radii O1’, O2’, O3’ etc. intersecting lines O1’, O2’, O3’ etc. at points P1, P2, P3 etc. respectively. In one revolution, P will reach the 12th division along QP and in the next half revolution it will be at the point PQ on the line 18'-0.
(iv) Draw a curve through points P, P1, P2, PQ. This curve is the required Archimedean spiral.
The constant of the curve is equal to the difference between the lengths of any two radii divided by the circular measure of the angle between them.
OP and OP3 (fig. 6-63) are two radii making go0 angle between them. In circular measure in radian,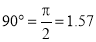
. Therefore, the constant of the curve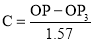 
Scales:
A scale is defined as the ratio of the linear dimensions of the object as represented in a drawing to the actual dimensions of the same.
Necessity
- Drawings drawn with the same size as the objects are called full sized drawing.
- It is not convenient, always, to draw drawings of the object to its actual size. e.g. Buildings, Heavy machines, Bridges, Watches, Electronic devices etc.
- Hence scales are used to prepare drawing at
Full size
Reduced size
Enlarged size
Types of Scale
- Engineers Scale :
The relation between the dimension on the drawing and the actual dimension of the object is mentioned numerically (like 10 mm = 15 m).
Mechanical Engineers Scale:
These are divided and numbered in such a way that fractions of inches represent inches. The most common ranges are 1/8, 1/4, 1/2, and 1 in. To the inch. These scales are known as the size scales because the reduced size also represents the ratio of size, as for example one-eighth size.
Mechanical engineer's scales are almost always "full divided"; that is, the smallest divisions run throughout the entire length.
They are generally graduated with the marked divisions numbered from right to left, as well as from left to right, as shown in Figure Mechanical engineer's scales are used mostly for drawings of machine parts and small structures where the drawing size is more than one-eighth the size of the actual object.
Civil Engineers Scale:
These are divided into decimals with divisions ranging from 10, 20, 30, 40, 50, 60, and 80 to the inch. Such a scale is usually full divided and is sometimes numbered both from left to right and right to leave. Civil engineer's scales are most used for plotting and drawing maps, although they are convenient for any work where divisions of the inch in tenths is required.
2. Graphical Scale:
Scale is drawn on the drawing itself. This takes care of the shrinkage of the engineer’s scale when the drawing becomes old.
Types of Graphical Scale
- Plain Scale
- Diagonal Scale
- Vernier Scale
- Comparative scale
- Plain Scale
- A plain scale consists of a line divided into suitable number of equal units. The first unit is subdivided into smaller parts.
- The zero should be placed at the end of the 1st main unit.
- From the zero mark, the units should be numbered to the right and the sub-divisions to the left.
- The units and the subdivisions should be labeled clearly.
2. Diagonal Scale
- Through Diagonal scale, measurements can be up to second decimal (e.g. 4.35).
- Diagonal scales are used to measure distances in a unit and its immediate two subdivisions; e.g. Dm, cm & mm, or yard, foot & inch.
- Diagonal scale can measure more accurately than the plain scale.
3. Vernier Scales
- Similar to Diagonal scale, Vernier scale is used for measuring up to second decimal.
- A Vernier scale consists of
(i) a primary scale and
(ii) a vernier.
- The primary scale is a plain scale fully divided in to minor divisions.
- The graduations on the vernier are derived from those on the Least count (LC) is the minimum distance that can be measured.
References:
1. Engineering Drawing N.D. Bhatt / Charotar
2. Engineering Drawing / N. S. Parthasarathy and Vela Murali/ Oxford
3. Engineering Drawing / Basant Agrawal and McAgrawal/ McGraw Hill
4. Engineering Drawing/ M. B. Shah, B.C. Rane / Pearson.
5. Computer Aided Engineering Drawing – K Balaveera Reddy et al – CBS Publishers
