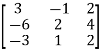UNIT-1
Matrices
Matrices: It is a rectangular arrangement of numbers formed by keeping them in m numbers of rows and n numbers of columns.
Types of matrices:
Row matrix:
A matrix with only one single row and many columns can be possible.
A = 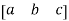
Column matrix
A matrix with only one single column and many rows can be possible.
A = 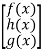
Square matrix
A matrix in which number of rows is equal to number of columns is called a square matrix. Thus an 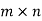 matrix is square matrix then m=n and is said to be of order n.
matrix is square matrix then m=n and is said to be of order n.
The determinant having the same elements as the square matrix A is called the determinant of the matrix A. Denoted by |A|.
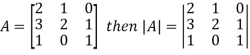
The diagonal elements of matrix A are 2, 2 and 1 is the leading and the principal diagonal.
The sum of the diagonal elements of square matrix A is called the trace of A.
A square matrix is said to be singular if its determinant is zero otherwise non-singular.
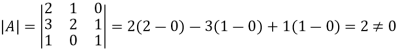
Hence the square matrix A is non-singular.
Diagonal matrix
A square matrix is said to be diagonal matrix if all its non diagonal elements are zero.
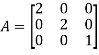
Scalar matrix:
A diagonal matrix is said to be scalar matrix if its diagonal elements are equal.
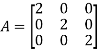
Identity matrix:
A square matrix in which elements in the diagonal are all 1 and rest are all zero is called an identity matrix or Unit matrix.
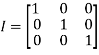
Null Matrix:
If all the elements of a matrix are zero, it is called a null or zero matrixes.
Ex: 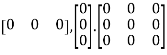 etc.
etc.
Symmetric matrix:
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 and
and 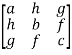
Example: check whether the following matrix A is symmetric or not?
A = 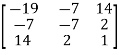
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,
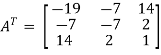
Here,
A = 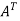
So that, the matrix A is symmetric.
Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
Sol. Suppose A is any square matrix .
Then,
A = 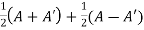
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Hermitian matrix:
A square matrix A = 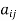 is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
It means,
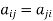
For example:
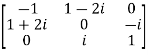
Necessary and sufficient condition for a matrix A to be hermitian –
A = (͞A)’
Skew-Hermitian matrix-
A square matrix A = 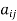 is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
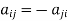
Note- all the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
For example:
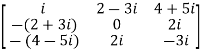
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-
- A = (͞A)’
Note: A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.
Similarly a Skew- Hermitian matrix is a generalization of a Skew symmetric matrix and also every Skew- symmetric matrix is Skew –Hermitian.
Theorem: Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
Or If A is given square complex matrix then 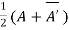 is hermitian and
is hermitian and 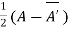 is skew-hermitian matrices.
is skew-hermitian matrices.
Example1: Express the matrix A as sum of hermitian and skew-hermitian matrix where 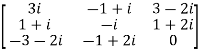
Let A =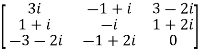
Therefore 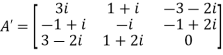 and
and 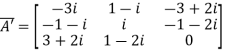
Let 
Again 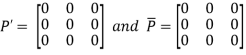
Hence P is a hermitian matrix.
Let 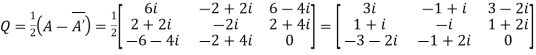
Again 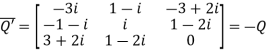
Hence Q is a skew- hermitian matrix.
We Check
P +Q=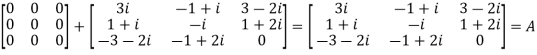
Hence proved.
Example2: If A = 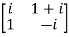 then show that
then show that
(i) 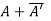 is hermitian matrix.
is hermitian matrix.
(ii) 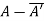 is skew-hermitian matrix.
is skew-hermitian matrix.
Given A = 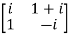
Then 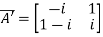
Let 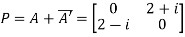
Also 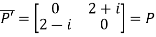
Hence P is a Hermitian matrix.
Let 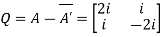
Also 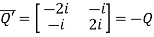
Hence Q is a skew-hermitian matrix.
Skew-symmetric matrix-
A square matrix A is said to be skew Symmetric matrix if –
1. A’ = -A, [ A’ is the transpose of A]
2.all the main diagonal elements will always be zero.
For example-
A = 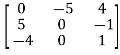
This is skew symmetric matrix, because transpose of matrix A is equals to negative A.
Example: check whether the following matrix A is symmetric or not?
A = 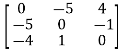
Sol. This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A.
-A = A’
Orthogonal matrix-
Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.
Such that,
A. A’ = I
Matrix × transpose of matrix = identity matrix
Note- if |A| = 1, then we can say that matrix A is proper.
Examples: 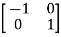 and
and 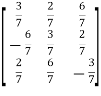 are the form of orthogonal matrices.
are the form of orthogonal matrices.
Unitary matrix-
A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
Such that,
( ͞A)’ . A = I
For example:
A = 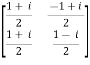 and its ( ͞A)’ =
and its ( ͞A)’ = 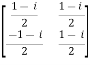
Then ( ͞A)’ . A = I
So that we can say that matrix A is said to be a unitary matrix.
Rank of a matrix by echelon form-
The rank of a matrix (r) can be defined as –
1. It has at least one non-zero minor of order r.
2. Every minor of A of order higher than r is zero.
Example: Find the rank of a matrix M by echelon form.
M = 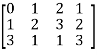
Sol. First we will convert the matrix M into echelon form,
M = 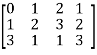
Apply, 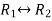 , we get
, we get
M = 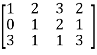
Apply 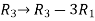 , we get
, we get
M = 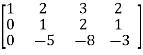
Apply 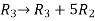
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Example: Find the rank of a matrix A by echelon form.
A = 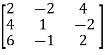
Sol. Convert the matrix A into echelon form,
A = 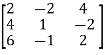
Apply 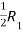
A = 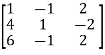
Apply 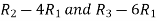 , we get
, we get
A = 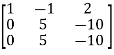
Apply 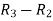 , we get
, we get
A = 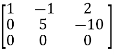
Apply 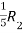 ,
,
A = 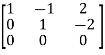
Apply 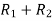 ,
,
A = 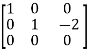
Therefore the rank of the matrix will be 2.
Example: Find the rank of a matrix A by echelon form.
A = 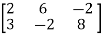
Sol. Transform the matrix A into echelon form, then find the rank,
We have,
A = 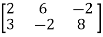
Apply, 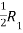
A = 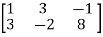
Apply 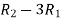 ,
,
A = 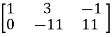
Apply 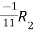
A = 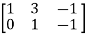
Apply 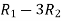
A = 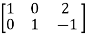
Hence the rank of the matrix will be 2.
Example: Find the rank of the following matrices by echelon form?
Let A = 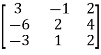
Applying 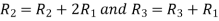
A 
Applying 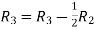
A 
Applying 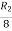
A 
Applying 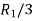
A 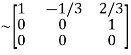
It is clear that minor of order 3 vanishes but minor of order 2 exists as 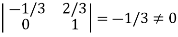
Hence rank of a given matrix A is 2 denoted by 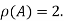
2. 
Let A = 
Applying 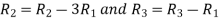

Applying 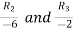
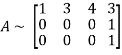
Applying 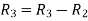
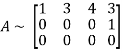
The minor of order 3 vanishes but minor of order 2 non zero as 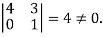
Hence the rank of matrix A is 2 denoted by 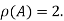
3. 
Let A = 
Apply 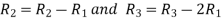

Apply 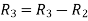

Apply 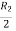
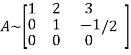
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as 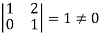
Hence the rank of given matrix is 2 i.e. 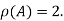
Rank of a matrix by normal form-
Any matrix ‘A’ which is non-zero can be reduced to a normal form of ‘A’ by using elementary transformations.
There are 4 types of normal forms –

The number r obtained is known as rank of matrix A.
Both row and column transformations may be used in order to find the rank of the matrix.
Note-Normal form is also known as canonical form
Example: reduce the matrix A to its normal form and find rank as well.


Sol. We have,

We will apply elementary row operation,
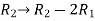
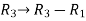
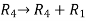
We get,
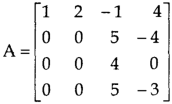
Now apply column transformation,
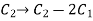
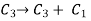
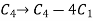
We get,

Apply
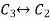 , we get,
, we get,

Apply 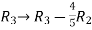 and
and 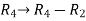

Apply 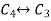

Apply 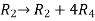 and
and 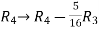

Apply 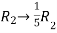 and
and 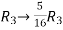

As we can see this is required normal form of matrix A.
Therefore the rank of matrix A is 3.
Example: Find the rank of a matrix A by reducing into its normal form.
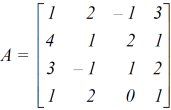
Sol. We are given,
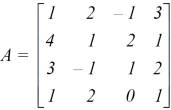
Apply
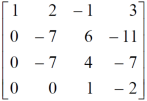
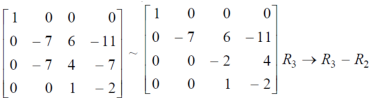
Apply
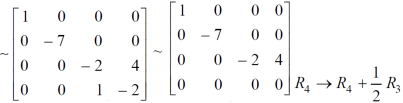
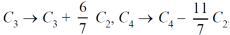
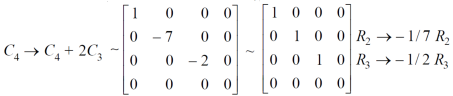
This is the normal form of matrix A.
So that the rank of matrix A = 3
If A (matrix) reduced to I by elementary transformation then
PA = I
P = A‾¹ where P is elementary matrix.
Example: Find the inverse of the following matrix by using gauss Jordan method.
Sol. Here we are given,
A = 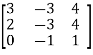
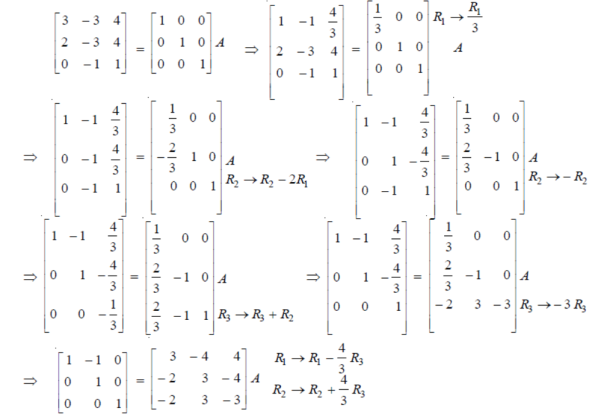
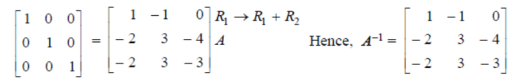
Example: Find the inverse of the following matrix by using gauss Jordan method.
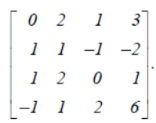
Sol. Let the matrix is A, then

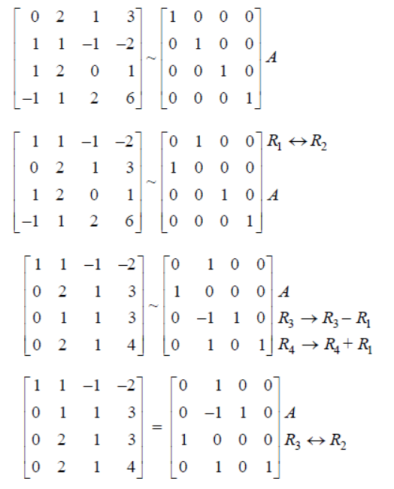
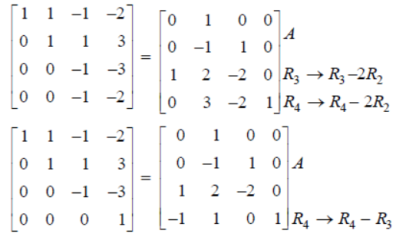
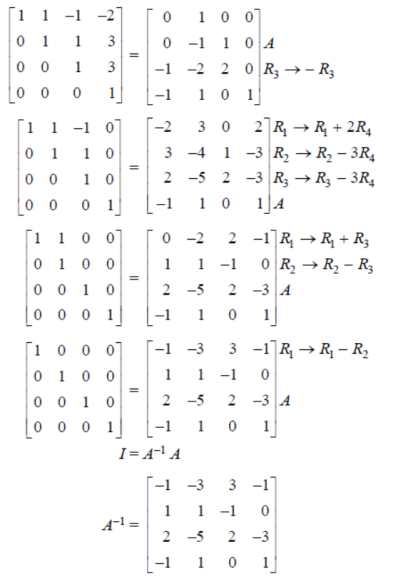
There are two types of linear equations-
1. Consistent 2. Inconsistent
Let’s understand about these two types of linear equations
Consistent –
If a system of equations has one or more than one solution, it is said be consistent.
There could be unique solution or infinite solution.
For example-
A system of linear equations-
2x + 4y = 9
x + y = 5
Has unique solution,
Whereas,
A system of linear equations-
2x + y = 6
4x + 2y = 12
Has infinite solutions.
Inconsistent-
If a system of equations has no solution, then it is called inconsistent.
Consistency of a system of linear equations-
Suppose that a system of linear equations is given as-




This is the format as AX = B
Its augmented matrix is-
[A:B] = C
(1) consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n ( no. Of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
(2) inconsistent equations-
If Rank of A ≠ Rank of C
Solution of homogeneous system of linear equations-
A system of linear equations of the form AX = O is said to be homogeneous, where A denotes the coefficients and of matrix and and O denotes the null vector.
Suppose the system of homogeneous linear equations is,



It means,
AX = O
Which can be written in the form of matrix as below,
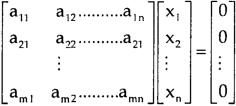
Note- A system of homogeneous linear equations always has a solution if
1. r(A) = n then there will be trivial solution, where n is the number of unknown,
2. r(A) < n , then there will be an infinite number of solution.
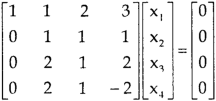
Example: Find the solution of the following homogeneous system of linear equations,
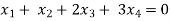
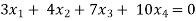
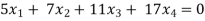
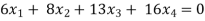
Sol. The given system of linear equations can be written in the form of matrix as follows,
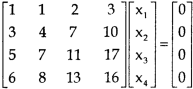
Apply the elementary row transformation,
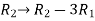
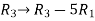
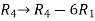 , we get,
, we get,
 , we get
, we get
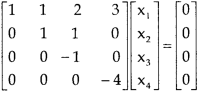
Here r(A) = 4, so that it has trivial solution,
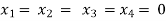
Example: Find out the value of ‘b’ in the system of homogeneous equations-
2x + y + 2z = 0
x + y + 3z = 0
4x + 3y + bz = 0
Which has
(1) trivial solution
(2) non-trivial solution
Sol. (1)
For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value.
Now for non-trivial solution-
(2)
Convert the system of equations into matrix form-
AX = O
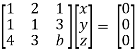
Apply 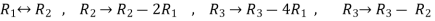 respectively , we get the following resultant matrices
respectively , we get the following resultant matrices
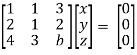
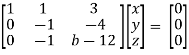
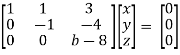
For non-trivial solutions, r(A) = 2 < n
b – 8 = 0
b = 8
Solution of non-homogeneous system of linear equations-
Example-1: check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
Sol. Write the above system of linear equations in augmented matrix form,
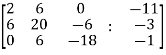
Apply 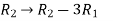 , we get
, we get
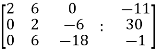
Apply 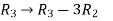
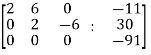
Here the rank of C is 3 and the rank of A is 2
Therefore both ranks are not equal. So that the given system of linear equations is not consistent.
Example: Check the consistency and find the values of x , y and z of the following system of linear equations.
2x + 3y + 4z = 11
X + 5y + 7z = 15
3x + 11y + 13z = 25
Sol. Re-write the system of equations in augmented matrix form.
C = [A,B]
That will be,
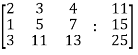
Apply 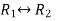
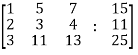
Now apply , 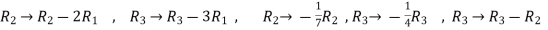
We get,
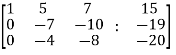 ~
~ 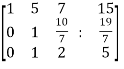 ~
~ 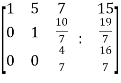
Here rank of A = 3
And rank of C = 3, so that the system of equations is consistent,
So that we can can solve the equations as below,
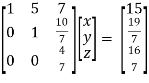
That gives,
x + 5y + 7z = 15 ……………..(1)
y + 10z/7 = 19/7 ………………(2)
4z/7 = 16/7 ………………….(3)
From eq. (3)
z = 4,
From 2,
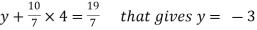
From eq.(1), we get
x + 5(-3) + 7(4) = 15
That gives,
x = 2
Therefore the values of x , y , z are 2 , -3 , 4 respectively.
Matrix form of the linear system can be written as follows,
Ax = b
Where,

A is called augmented matrix.
Gauss elimination method can be presented as ,
Suppose there is a linear system in triangular form ,
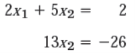
We can solve this as X2 = -26/13 = -2 and X1 = 6
Lets another set of eq. Is given as ,
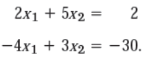
Its augmented matrix is given by,
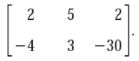
We eliminate X1 from the second eq.
To get the triangular system . We add twice the first equation to the second and we do same operation on rows of the augmented matrix. This gives,
-4X1 +4X1 +3X2 + 10X2 = -30 + 2.2
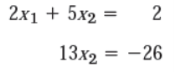
This is called Gauss elimination.
Example: find the solution of the following linear equations.
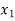 +
+ 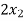 -
- 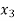 = 1
= 1
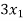 -
- 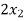 +
+ 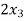 = 2
= 2
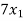 - 2
- 2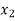 +
+ 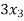 = 5
= 5
Sol. These equations can be converted into the form of matrix as below-
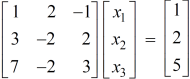
Apply the operation, 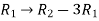 and
and 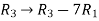 , we get
, we get
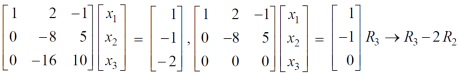
We get the following set of equations from the above matrix,
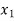 +
+ 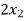 -
- 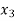 = 1 …………………..(1)
= 1 …………………..(1)
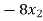 + 5
+ 5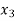 = -1 …………………(2)
= -1 …………………(2)
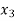 = k
= k
Put x = k in eq. (1)
We get,
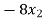 + 5k = -1
+ 5k = -1
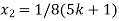
Put these values in eq. (1), we get
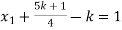
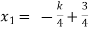
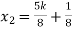 and
and 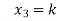
These equations have infinitely many solutions.
Step by step method to solve the system of linear equation by using Gauss Seidel iteration method-
Suppose,
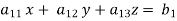
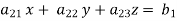
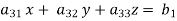
This system can be written as after dividing it by suitable constants,
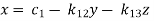
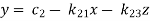
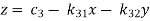
Step-1 Here put y = 0 and z = 0 and x = 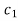 in first equation
in first equation
Then in second equation we put this value of x that we get the value of y.
In the third eq. We get z by using the values of x and y
Step-2: we repeat the same procedure
Example: solve the following system of linear equations by using Gauss seidel method-
6x + y + z = 105
4x + 8y + 3z = 155
5x + 4y - 10z = 65
Sol. The above equations can be written as,
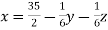 ………………(1)
………………(1)
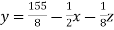 ………………………(2)
………………………(2)
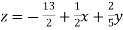 ………………………..(3)
………………………..(3)
Now put z = y = 0 in first eq.
We get
x = 35/2
Put x = 35/2 and z = 0 in eq. (2)
We have,
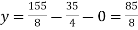
Put the values of x and y in eq. 3
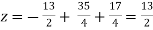
Again start from eq.(1)
By putting the values of y and z
y = 85/8 and z = 13/2
We get
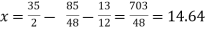
The process can be showed in the table format as below
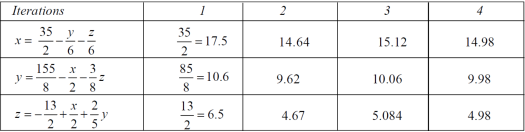
At the fourth iteration , we get the values of x = 14.98 , y = 9.98 , z = 4.98
Which are approximately equal to the actual values,
As x = 15 , y = 10 and y = 5 ( which are the actual values)
Example: : solve the following system of linear equations by using Gauss seidel method-
5x + 2y + z = 12
x + 4y + 2z = 15
x + 2y + 5z = 20
Sol. These equations can be written as ,
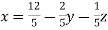 ………………(1)
………………(1)
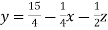 ………………………(2)
………………………(2)
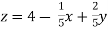 ………………………..(3)
………………………..(3)
Put y and z equals to 0 in eq. 1
We get,
x = 2.4
Put x = 2.4, and z = 0 in eq. 2 , we get
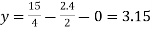
Put x = 2.4 and y = 3.15 in eq.(3) , we get
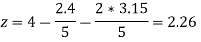
Again start from eq.(1), put the values of y and z , we get
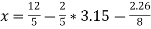 = 0.688
= 0.688
We repeat the process again and again ,
The following table can be obtained –
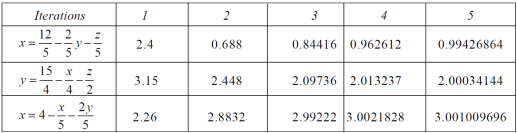

We see that the values are apprx. Equal to exact values.
Exact values are , x = 1 , y = 2, z = 3.