UNIT 2
A.C. Circuits
Sinusoidal Waveform Construction
Coil Angle ( θ ) | 0 | 45 | 90 | 135 | 180 | 225 | 270 | 315 | 360 |
e = Vmax.sinθ | 0 | 70.71 | 100 | 70.71 | 0 | -70.71 | -100 | -70.71 | -0 |
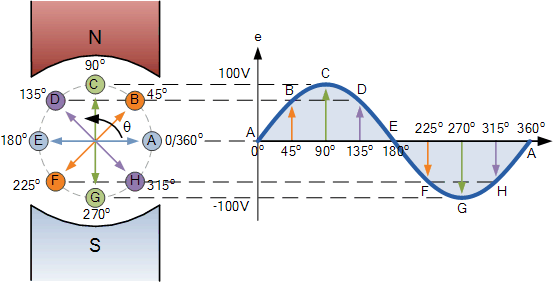
The points on the sinusoidal waveform are obtained by projecting across from the various positions of rotation between 0o and 360o to the ordinate of the waveform that corresponds to the angle, θ and when the wire loop or coil rotates one complete revolution, or 360o, one full waveform is produced.
From the plot of the sinusoidal waveform we can see that when θ is equal to 0o, 180o or 360o, the generated EMF is zero as the coil cuts the minimum amount of lines of flux. But when θ is equal to 90o and 270o the generated EMF is at its maximum value as the maximum amount of flux is cut.
Therefore a sinusoidal waveform has a positive peak at 90o and a negative peak at 270o. Positions B, D, F and H generate a value of EMF corresponding to the formula: e = Vmax.sinθ.
Then the waveform shape produced by our simple single loop generator is commonly referred to as a Sine Wave as it is said to be sinusoidal in its shape. This type of waveform is called a sine wave because it is based on the trigonometric sine function used in mathematics, ( x(t) = Amax.sinθ ).
Average Value:
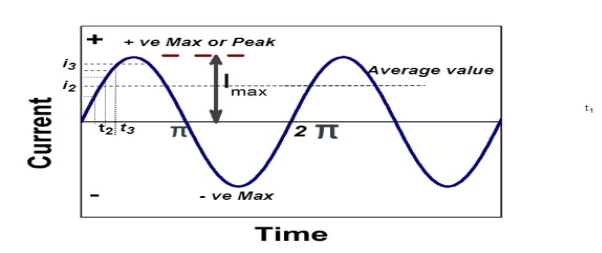
The arithmetic mean of all the value over complete one cycle is called as average value
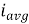 =
= 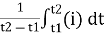
For the derivation we are considering only hall cycle.
Thus  varies from 0 to ᴫ
varies from 0 to ᴫ
i = Im Sin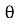
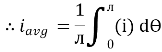
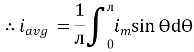
Solving
We get
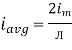
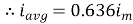
Similarly, Vavg=
The average value of sinusoid ally varying alternating current is 0.636 times maximum value of alternating current.
RMS value: Root mean square value
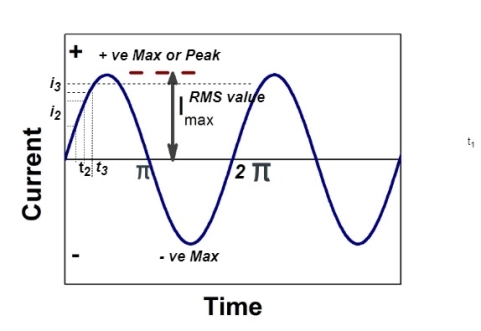
The RMS value of AC current is equal to the steady state DC current that required to produce the same amount of heat produced by ac current provided that resistance and time for which these currents flows are identical.
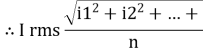
I rms = 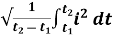
Direction for RMS value:
Instantaneous current equation is given by
i = Im Sin 
But 
I rms = 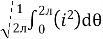
= 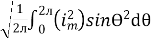
=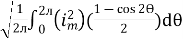
=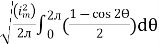
Solving
=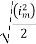
=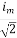
Similar we can derive
V rms= 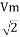 or 0.707 Vm
or 0.707 Vm
 the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
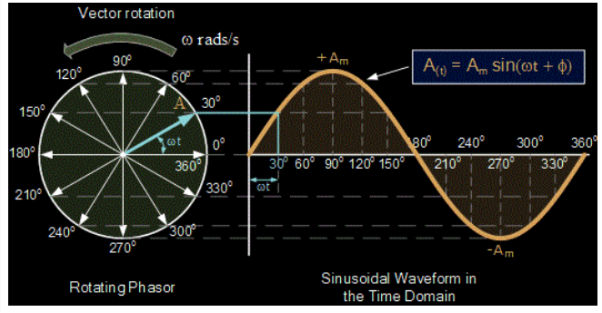
A phasor is a vector that is used to represent a sinusoidal function. It rotates about the origin with an angular speed ω.
The vertical component of phasors represents the quantities that are sinusoidally varying for a given equation, such as v and i. Here, the magnitude of the phasors represents the peak value of the voltage and the current.
From the figure shown above, we can see the relation between a phasor and the sinusoidal representation of the function with respect to time. The projection of the phasor on the vertical axis represents the value of the quantity.
For example, in the case of a current or a vector phasor, the projection of the phasor on the vertical axis, given by vmsinωt and imsinωt respectively, gives the value of the current or the voltage at that instant.
From the phasor diagram, it is easy to detect that one of two quantities are in the same phase. For example, if for a given circuit, the phasors for the voltage and the current are in the same direction for all instances, the phase angle between the voltage and the current is zero.
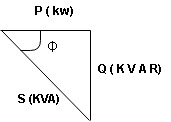
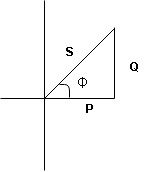
- Apparent power (S) : it is defined as product of rms value of voltage (V) and current (I) or it is the total power / max power
S = V 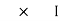
 Unit - volt – Ampere (VA)
Unit - volt – Ampere (VA)
In kilo – K. V. A.
2. Real power / true power / active power / useful power : [P] it is defined as the product of rms value active component or it is the average power or actual power consumed by the resistive part (R) in the given combinational circuit
It is measured in watts
P = VI Cos Ø watts /km where Ø is the power factor angle
3. Reactive power / Imaginary / useless power [Q]
It is defined as the product of voltage current and sine of angle between V and
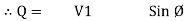
Volt Amp Relative
 Unit – V A R
Unit – V A R
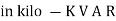
 Power triangle
Power triangle
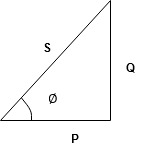
- As we know power factor is cosine of angle between voltage and current
i e P.F. = Cos 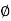
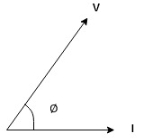
In other words also we can derive it from impedance triangle
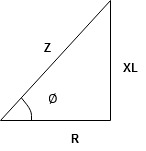
Now consider Impedance triangle in R – L- ckt.
From  now Cos
now Cos  = power factor =
= power factor = 
 power factor = Cos
power factor = Cos  or
or 
Reactance
- Inductive Reactance (XL)
It is opposition to the flow of an AC current offered by inductor.
XL = ω L But ω = 2 ᴫ F
 XL = 2 ᴫ F L
XL = 2 ᴫ F L
It is measured in ohm
 XL∝FInductor blocks AC supply and passes dc supply zero
XL∝FInductor blocks AC supply and passes dc supply zero
2. Capacitive Reactance (Xc)
It is opposition to the flow of ac current offered by capacitor
Xc = 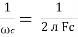
Measured in ohm
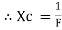 Capacitor offers infinite opposition to dc supply
Capacitor offers infinite opposition to dc supply 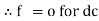
Impedance (Z)
The ac circuit is to always pure R pure L and pure C it well attains the combination of these elements. “The combination of R1 XL and XC is defined and called as impedance represented as
Z = R +i X
Ø = 0
 only magnitude
only magnitude
R = Resistance, i = denoted complex variable, X =Reactance XL or Xc
Polar Form
Z = 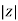 L I
L I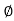
Where 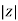 =
=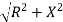
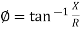 Measured in ohm
Measured in ohm
Power factor (P.F.)
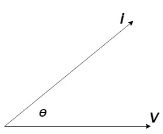
It is the cosine of angle between voltage and current
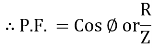
If Ɵis –ve or lagging (I lags V) then lagging P.F.
If Ɵ is +ve or leading (I leads V) then leading P.F.
If Ɵ is 0 or in phase (I and V in phase) then unity P.F.
Ac circuit containing pure resisting
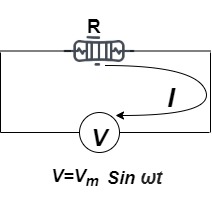
Consider Circuit Consisting pure resistance connected across ac voltage source
V = Vm Sin ωt ①
According to ohm’s law i =  =
= 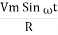
But Im = 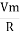
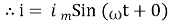 ②
②
From ① and ②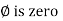 phase or represents RMD value.
phase or represents RMD value.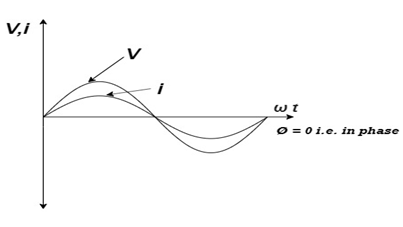
Power P = V. i
Equation P = Vm sin ω t Im sin ω t
P = Vm Im Sin2 ω t
P = 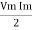 -
- 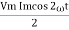
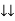
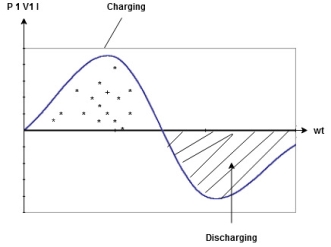
Constant fluctuating power if we integrate it becomes zero
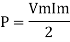
Average power
Pavg = 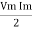
Pavg = 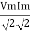
Pavg = Vrms Irms
Power ware form [Resultant]
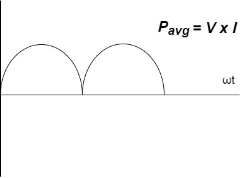
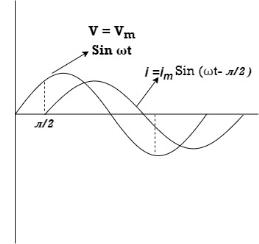
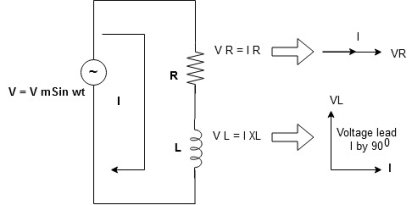
Ac circuit containing pure Inductors

Consider pure Inductor (L) is connected across alternating voltage. Source
V = Vm Sin ωt
When an alternating current flow through inductance it set ups alternating magnetic flux around the inductor.
This changing the flux links the coil and self-induced emf is produced
According to faradays Law of E M I
e = 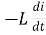
At all instant applied voltage V is equal and opposite to self-induced emf [ lenz’s law]
V = -e
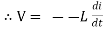 =
= 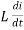
But V = Vm Sin ωt
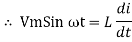
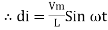 dt
dt
Taking integrating on both sides
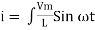 dt
dt
 dt
dt
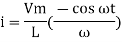
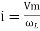 (-cos
(-cos 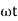 )
)
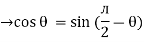
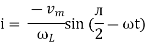
But sin (–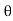 ) = sin (+
) = sin (+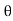 )
)
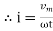 sin (
sin (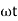 -
- 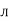 /2)
/2)
And Im= 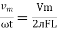
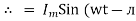 /2)
/2)
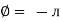 /2
/2
= -ve
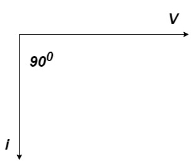
= lagging
= I lag v by 900
Waveform:
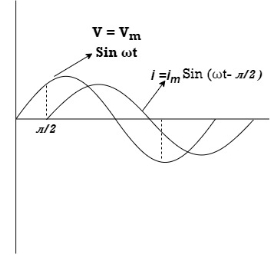
Phasor:
Power P = Ѵ. I
= Vm sin wt Im sin (wt 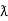 /2)
/2)
= Vm Im Sin wt Sin (wt – 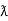 /s)
/s)
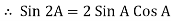 ①
①
And
Sin (wt - 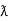 /s) = - cos wt ②
/s) = - cos wt ②
Sin (wt – 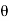 ) = - cos
) = - cos 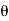
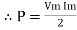 sin 2 wt from ① and ②
sin 2 wt from ① and ②
The average value of sin curve over a complete cycle is always zero
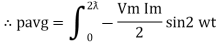
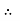 Pavg = 0
Pavg = 0
Ac circuit containing pure capacitors:
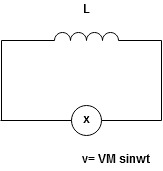
Consider pure capacitor C is connected across alternating voltage source
Ѵ = Ѵm Sin wt
Current is passing through capacitor the instantaneous charge ɡ produced on the plate of capacitor
ɡ = C Ѵ
ɡ = c Vm sin wt
The current is rate of flow of charge
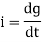
i=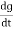 (cvm sin wt)
(cvm sin wt)
i = c Vm w cos wt
Then rearranging the above eqth.
i = 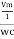 cos wt
cos wt
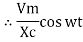
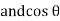 = sin (wt +
= sin (wt + 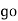 X/2)
X/2)
i = 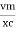 sin (wt + X/2)
sin (wt + X/2)
But 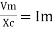
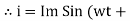 X/2)
X/2)
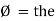
= leading
= I leads V by 900
Waveform :
Phase
Power P= Ѵ. i
= [Vm sinwt] [ Im sin (wt + X/2)]
= Vm Im Sin wt Sin (wt + X/2)]
 (cos wt)
(cos wt)
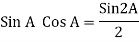
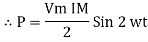
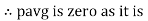 to charging power waveform [resultant].
to charging power waveform [resultant].
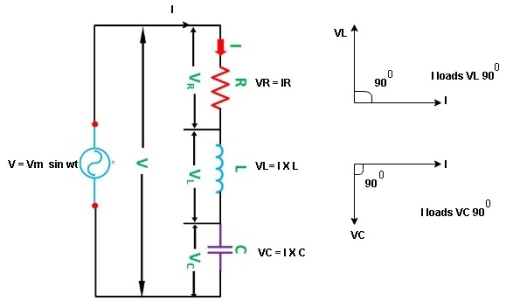
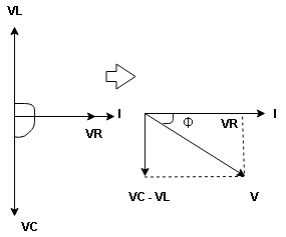
Series R-L Circuit
Consider a series R-L circuit connected across voltage source V= Vm sin wt
As some I is the current flowing through the resistor and inductor due do this current voltage drops arcos R and L R  VR = IR and L
VR = IR and L  VL = I X L
VL = I X L
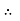 Total V = VR + VL
Total V = VR + VL
V = IR + I X L  V = I [R + X L]
V = I [R + X L]
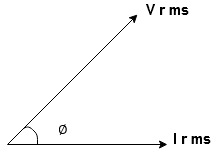
Take current as the reference phasor : 1) for resistor current is in phase with voltage 2) for Inductor voltage leads current or current lags voltage by 90 0.
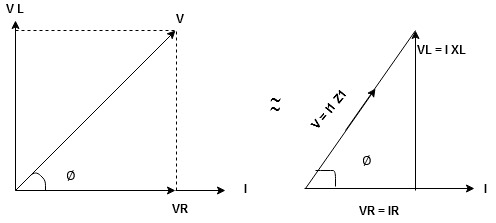
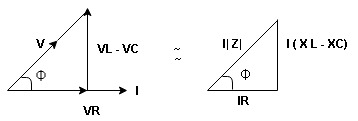
For voltage triangle
Ø is power factor angle between current and resultant voltage V and
V = 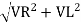
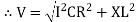
V = 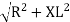
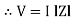
Where Z = Impedance of circuit and its value is 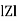 =
= 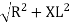
Impedance Triangle
Divide voltage triangle by I
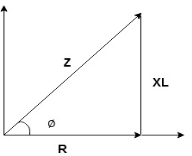
Rectangular form of Z = R+ixL
And polar from of Z =  L +
L + 
(+ j X L + 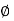 because it is in first quadrant )
because it is in first quadrant )
Where 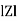 =
= 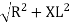
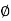 + Tan -1
+ Tan -1 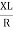
Current Equation :
From the voltage triangle we can sec. That voltage is leading current by 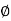 or current is legging resultant voltage by
or current is legging resultant voltage by 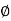
Or i = 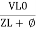 =
= 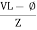 [ current angles - Ø )
[ current angles - Ø )

Resultant Phasor Diagram from Voltage and current eq.
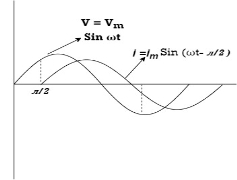
Wave form
Power equation
P = V .I.
P = Vm Sin wt Im Sin wt – Ø
P = Vm Im (Sin wt) Sin (wt – Ø)
P = 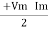 (Cos Ø) - Cos (2wt – Ø)
(Cos Ø) - Cos (2wt – Ø)
Since 2 sin A Sin B = Cos (A-B) – Cos (A+B)
P = 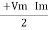 Cos Ø -
Cos Ø - 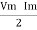 Cos (2wt – Ø)
Cos (2wt – Ø)
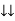
①②
Average Power
Pang = 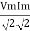 Cos Ø
Cos Ø
Since ② term become zero because Integration of cosine come from 0 to 2ƛ
 pang = Vrms Irms cos Ø watts.
pang = Vrms Irms cos Ø watts.
Power Triangle :
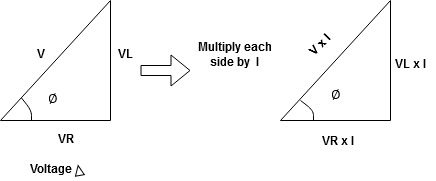
From 
VI = VRI + VLI B
Now cos Ø in  A =
A = 
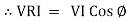 ①
①
Similarly Sin 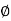 =
= 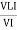

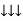
Apparent Power Average or true Reactive or useless power
Or real or active
-Unit (VI) Unit (Watts) C/W (VAR) denoted by (Ø)
Denoted by [S] denoted by [P]
Power 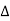 for R L ekt.
for R L ekt.

Series R-C circuit
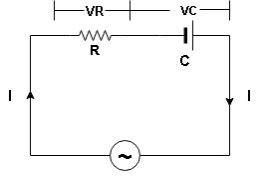
V = Vm sin wt
VR

 I
I
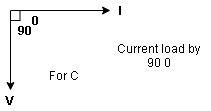
- Consider a series R – C circuit in which resistor R is connected in series with capacitor C across a ac voltage so use V = VM Sin wt. (voltage equation).
- Assume Current I is flowing through
R and C  voltage drops across.
voltage drops across.
R and C  R
R 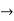 VR = IR
VR = IR
And C  Vc = I
Vc = I c
c
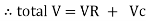
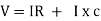
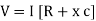
 V =
V = 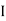 lZl
lZl
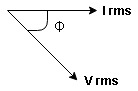
Voltage triangle: take current as the reference phasor 1) for resistor current is in phase with voltage 2) for capacitor current leads voltage or voltage lags behind current by 900
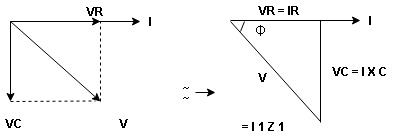
Where Ø is power factor angle between current and voltage (resultant) V
And from voltage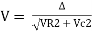
V = 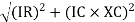
V = 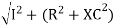
V = 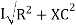
V = 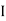 lZl
lZl
Where Z = impedance of circuit and its value is lZl = 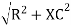
Impendence triangle:
Divide voltage  by
by  as shown
as shown
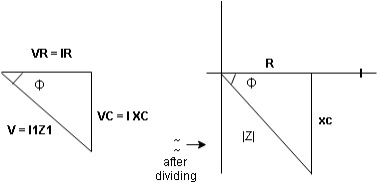
Rectangular from of Z = R - jXc
Polar from of Z = lZl L - Ø
( - Ø and –jXc because it is in fourth quadrant ) where
LZl = 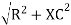
And Ø = tan -1 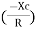
Current equation:
From voltage triangle we can see that voltage is lagging current by Ø or current is leading voltage by Ø
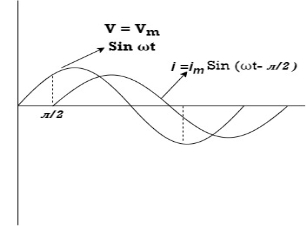
 i = IM Sin (wt + Ø) since Ø is +ve
i = IM Sin (wt + Ø) since Ø is +ve
Or i = 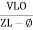 for RC
for RC
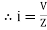 LØ [ resultant current angle is + Ø]
LØ [ resultant current angle is + Ø]
Resultant phasor diagram from voltage and current equation
Resultant wave form :
Power Equation :
P = V. I
P = Vm sin wt. Im Sin (wt + Ø)
= Vm Im sin wt sin (wt + Ø)
2 Sin A Sin B = Cos (A-B) – Cos (A+B)
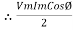 -
- 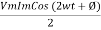
Average power
Pang = 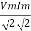 Cos Ø
Cos Ø
Since 2 terms integration of cosine wave from 0 to 2ƛ become zero
 2 terms become zero
2 terms become zero
 pang = Vrms Irms Cos Ø
pang = Vrms Irms Cos Ø
Power triangle RC Circuit:
R-L-C series circuit
Consider ac voltage source V = Vm sin wt connected across combination of R L and C. When I flowing in the circuit voltage drops across each component as shown below.
VR = IR, VL = I  L, VC = I
L, VC = I  C
C
- According to the values of Inductive and Capacitive Reactance I e XL and XC decides the behaviour of R-L-C series circuit according to following conditions
① XL> XC, ② XC> XL, ③ XL = XC
① XL > XC: Since we have assumed XL> XC
 Voltage drop across XL> than XC
Voltage drop across XL> than XC
 VL> VC A
VL> VC A
- Voltage triangle considering condition A
VL and VC are 180 0 out of phase .
Therefore, cancel out each other
 Resultant voltage triangle
Resultant voltage triangle
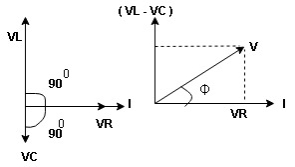
Now V = VR + VL + VC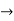 c phasor sum and VL and VC are directly in phase opposition and VL
c phasor sum and VL and VC are directly in phase opposition and VL VC
VC their resultant is (VL - VC).
their resultant is (VL - VC).
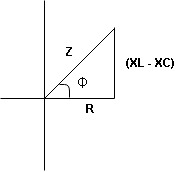
From voltage triangle
V = 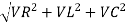
 V =
V = 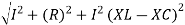
 V = I
V = I 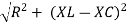
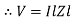
Impendence  : divide voltage
: divide voltage 
Rectangular form Z = R + j (XL – XC)
Polor form Z = 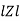 l + Ø B
l + Ø B
Where 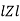 =
= 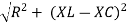
And Ø = tan-1 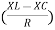
- Voltage equation : V = Vm Sin wt
- Current equation
i = 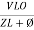 from B
from B
i =  L-Ø C
L-Ø C
As VL VC the circuit is mostly inductive and
VC the circuit is mostly inductive and  I lags behind V by angle Ø
I lags behind V by angle Ø
 Since i =
Since i =  L-Ø
L-Ø
 i = Im Sin (wt – Ø) from c
i = Im Sin (wt – Ø) from c
- XC
 XL :Since we have assured XC
XL :Since we have assured XC  XL
XL
 the voltage drops across XC
the voltage drops across XC  than XL
than XL
 XC
XC  XL (A)
XL (A)
 voltage triangle considering condition (A)
voltage triangle considering condition (A)
 Resultant Voltage
Resultant Voltage 
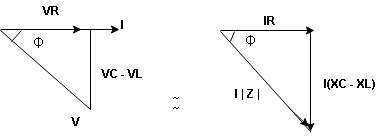
Now V = VR + VL + VC  phases sum and VL and VC are directly in phase opposition and VC
phases sum and VL and VC are directly in phase opposition and VC VL
VL  their resultant is (VC – VL)
their resultant is (VC – VL)
From voltage 
V = 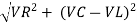
V = 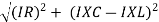
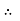 V =
V = 
 V =
V = 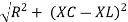
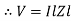
 Impedance
Impedance 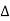 : Divide voltage
: Divide voltage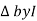
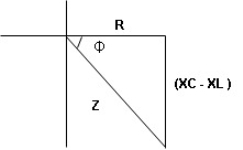
- Rectangular form : Z + R – j (XC – XL) – 4th qurd
Polar form : Z = 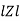 L -
L -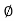
Where 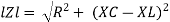
And Ø = tan-1 – 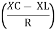
- Voltage equation : V = Vm Sin wt
- Current equation : i =
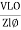 from B
from B - i =
 L+Ø C
L+Ø C
As VC 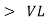 the circuit is mostly capacitive and
the circuit is mostly capacitive and 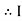 leads voltage by angle Ø
leads voltage by angle Ø
Since i = 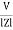 L + Ø
L + Ø
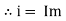 Sin (wt – Ø) from C
Sin (wt – Ø) from C
- Power
 :
:
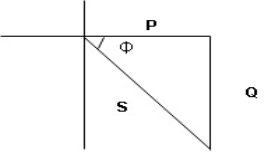
- XL= XC (resonance condition):
ɡȴ XL= XC then VL= VC and they are 1800 out of phase with each other  they will cancel out each other and their resultant will have zero value.
they will cancel out each other and their resultant will have zero value.
Hence resultant V = VR and it will be in phase with I as shown in below phasor diagram.
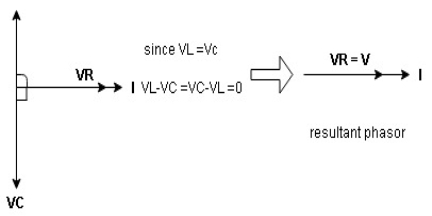
From above resultant phasor diagram
V =VR + IR
Or V = I  lZl
lZl
Because lZl + R
Thus Impedance Z is purely resistive for XL = XC and circuit current will be in phase with source voltage.
Since VR=V Øis zero when XL = XC  power is unity
power is unity
Ie pang = Vrms I rms cos Ø = 1 cos o = 1
Maximum power will be transferred by condition. XL = XC
Resonance in series RLC circuits
Definition: it is defined as the phenomenon which takes place in the series or parallel R-L-C circuit which leads to unity power factor
Voltage and current in R – L - C ckt. Are in phase with each other
Resonance is used in many communicate circuit such as radio receiver.
Resonance in series RLC series resonance in parallel RLC anti resonance / parallel resonance.
- Condition for resonance XL = XC
- Resonant frequency (Fr) : for given values of R-L-C the inductive reactance XL become exactly equal to the capacitive reactance Xc only at one particular frequency. This frequency is called as resonant frequency and denoted by (fr)
- Expression for resonant frequency(fr) : we know that XL = 2ƛ FL - Inductive reactance
Xc = 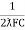 - capacitive reactance
- capacitive reactance
At a particular frequency ȴ = fr, the Inductive and capacitive reactance are exactly equal
 XL = XC ……at ȴ = fr
XL = XC ……at ȴ = fr
Ie 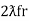 L =
L = 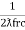
 fr2 =
fr2 = 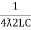
 fr =
fr = 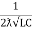 H2
H2
And 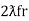 = wr =
= wr = 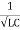 rad/sec
rad/sec
Three phase circuit is the polyphase system where three phases are sent together from generator to the load. Each phase are having a phase difference of 1200, i.e 1200 angle electrically. So from the total of 3600, three phase are equally divided into 1200 each. The power in three phase system is continuous as all the three phases are involved in generating the total power. The sinusoidal waves for 3 phase system is shown below
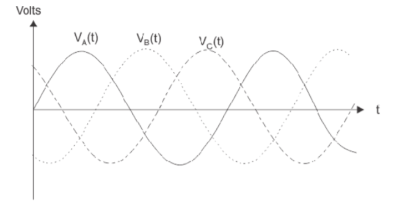
The three- phase can be used as single phase each. So, if the load is single phase, then one phase can be taken from the three- phase circuit and the neutral can be used as ground to complete the circuit.
A set of three impedances interconnected in the form of a star or delta form a 3-phase star or delta connected load. If the three impedances are identical and equal then it is a balanced 3-phase load, otherwise it is an unbalanced 3-phase load.
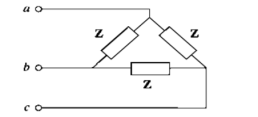
Let us consider a balanced 3-phase delta connected load
Determination of phase voltages:
VAB = V∠0 0 , VBC = V∠-1200 , VCA = V∠ − 240 0 = V∠120 0
Determination of phase currents:
Phase current = Phase voltage/ Load impedance
IAB = VAB/ Z ; IBC = VBC/Z ; ICA = VCA/Z
Determination of line currents:
Line currents are calculated by applying KCL at nodes A,B,C
IA = IAB – ICA ; IB = IBC - IAB ; IC = ICA - IBC
Balanced star connected load:
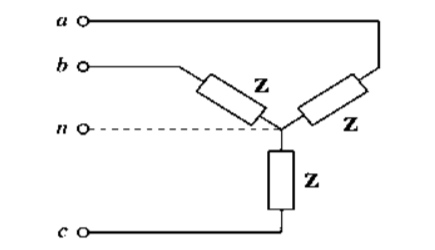
Let us consider a balanced 3-phase star connected load.
For star connection, phase voltage= Line voltage/(√3)
For ABC sequence, the phase voltage is polar form are taken as
VAN = Vph <-90 ; VCN = Vph<150 ; VBN = Vph <30
For star connection line currents and phase currents are equal
IA = VAN / Z ; IB = VBN/Z ; IC = VCN/Z
To determine the current in the neutral wire apply KVL at star point
IN + IA + IB + IC =0
IN = -(IA + IB + IC) since they are balanced.
In a balanced system the neutral current is zero. Hence if the load is balanced, the current and voltage will be same whether neutral wire is connected or not. Hence for a balanced 3-phase star connected load, whether the supply is 3- phase 3 wire or 3-phase 4 wire, it is immaterial. In case of unbalanced load, there will be neutral current.
Text-Books/Reference-Books:
- Basic Electrical Engineering - D.P. Kothari and I.J. Nagrath, 3rd edition 2010, Tata McGraw Hill.
- D.C. Kulshreshtha, “Basic Electrical Engineering”, McGraw Hill, 2009.
- L.S. Bobrow, Fundamentals of Electrical Engineering”, Oxford University Press, 2011
- Electrical and Electronics Technology, E. Hughes, 10th Edition, Pearson, 2010
- Electrical Engineering Fundamentals, Vincent Deltoro, Second Edition, Prentice Hall India, 1989.