Unit–4
Applied Statistics
Significance test of a sample mean
Given a random small sample 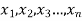 from a normal population we have to test the hypothesis that mean of the population is μ. For this we first calculate
from a normal population we have to test the hypothesis that mean of the population is μ. For this we first calculate 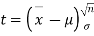
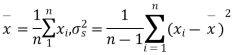
Then find the value of P for the given df from the table.
If the calculated value of 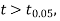 the difference between
the difference between  and μ is said to be significant at 5% level of significance.
and μ is said to be significant at 5% level of significance.
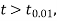 the difference is said to be significant at 1% level of significance.
the difference is said to be significant at 1% level of significance.
If 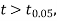 the data is said to be the consistent with the hypothesis that μ is the mean of the population.
the data is said to be the consistent with the hypothesis that μ is the mean of the population.
Example. A certain stimulus administered to each of 12 patients resulted in the following increases off blood pressure: 5, 2, 8, -1, 3, 0, -2, 1, 5, 0, 4, 6. Can it be concluded that the stimulus will in general be accompanied by an increase in blood pressure.
Solution. Let us assume that the stimulus administered to all the 12 patients will increases the blood pressure. Taking the population to be normal with mean μ = 0 and S.D. 
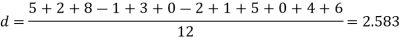
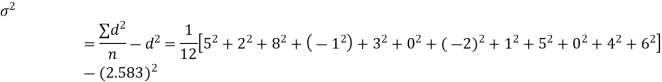
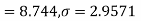
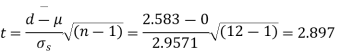
Here 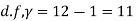
For 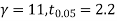 , from table IV.
, from table IV.
Since the  our assumptions is rejected i.e. the stimulus does not increase the B.P.
our assumptions is rejected i.e. the stimulus does not increase the B.P.
Example. The 9 items of a sample have the following values : 45, 47, , 50, 52, 48, 47, 49, 53, 51. Does the mean of these differ significantly from the assumed mean of 47.5?
Solution. We find the mean and the standard deviation of the sample as follows
x |  |  |
45 | -3 | 9 |
47 | -1 | 1 |
50 | 2 | 4 |
52 | 2 | 4 |
48 | 0 | 0 |
47 | -1 | 1 |
49 | 1 | 1 |
53 | 5 | 25 |
51 | 3 | 9 |
Total | 10 | 66 |
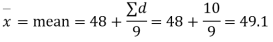
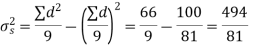
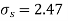
Hence, 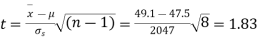
Here, 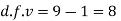
For v = 8, we get from table IV 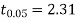
As calculated value of 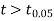 the value of t is not significant at 5% level of significance which implies that there is no significant difference between
the value of t is not significant at 5% level of significance which implies that there is no significant difference between 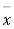 and μ. Thus the test provides no evidence against the population mean being 47.5.
and μ. Thus the test provides no evidence against the population mean being 47.5.
Example. A mechanism is making engine parts with axle diameter of 0.7 inch. A random sample of 10 parts shows mean diameter 0.742 inches with a standard deviation of 0.04 inch. On the basis of this sample would you say that the work is inferior?
Solution. Here we have,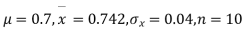
Taking the hypothesis that the product is not inferior that is there is no significant difference between 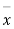 and μ.
and μ.
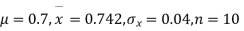
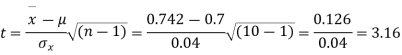
Degree of freedom 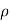 = 10-1=9
= 10-1=9
For  we get from table IV,
we get from table IV, 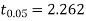
As the calculated value of 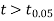 the value of t is significant at 5% level of significance. This implies that
the value of t is significant at 5% level of significance. This implies that 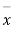 differs significantly from μ and the hypothesis is rejected. Hence the work is inferior. In fact the work is inferior even at 2% level of significance.
differs significantly from μ and the hypothesis is rejected. Hence the work is inferior. In fact the work is inferior even at 2% level of significance.
Comparison of large samples
Two large samples of sizes 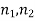 are taken from two populations giving proportions of attributes A's are
are taken from two populations giving proportions of attributes A's are 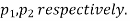
(a) On the hypothesis that the populations are similar as regards the attribute A, we combine the two samples to find an estimate of the common value of proportion of A’s in the populations which is given by
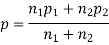
If 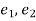 be the standard errors in the two samples then
be the standard errors in the two samples then
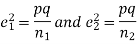
If e with the standard error of the difference between 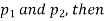
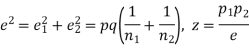
If z>3, the difference between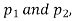 is real one.
is real one.
If z<2, the difference may be due to fluctuations of simple sampling.
But if z lies between 2 and 3, then the difference is significant at 5% level of significance.
(b)If the proportions of A's are not the same in the two populations from which the samples are drawn but 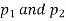 are the True values of proportions then S.E., e off the difference
are the True values of proportions then S.E., e off the difference 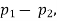 is given by
is given by
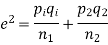
If 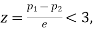 the difference could have rising due to fluctuations of simple sampling.
the difference could have rising due to fluctuations of simple sampling.
Example. In two large populations there are 30% and 25% respectively of fair haired people. Is this difference likely to be hidden in samples of 1200 and 900 respectively from the two populations?
Solution. Here 
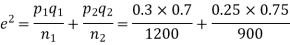
So that,. 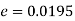

Hence it is unlikely that the real difference will be hidden.
Example. One type of aircraft is found to be develop engine trouble in 5 flights out of a total of hundred and another type in 7 flights out of a total of 200 flights. Is there a significant difference in the two types of aircraft so as far as engine defects are concerned.
Solution. 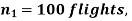 number of troubled flights =5
number of troubled flights =5

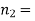 200 flights, number of troubled flights
200 flights, number of troubled flights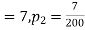
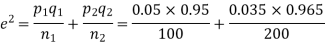

e=0.0254
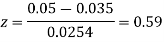
z<1, difference is not significant.
Example. In a sample of 600 men from a certain City 450 are found smokers. In another sample of 900 men from another City, 450 are smokers. Do the data indicate that the cities are significantly different with respect to the habit of smoking among men.
Solution. 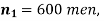 number of smokers = 450,
number of smokers = 450, 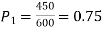
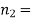 900 men, number of smokers = 450,
900 men, number of smokers = 450, 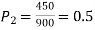
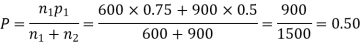
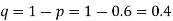
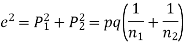
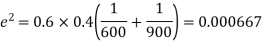

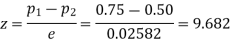
z>3 so that the difference is significant.
Significance test of difference between sample mean
Given two independent samples, 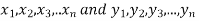 which means
which means  and standard deviations from a normal population with the same variance, we have to test the hypothesis that the population means
and standard deviations from a normal population with the same variance, we have to test the hypothesis that the population means  are the same
are the same
For this, we calculate,
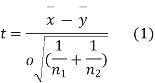
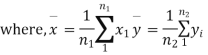

It can be shown that the variate t defined by (1) follows the t distribution with 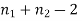 degree of freedom.
degree of freedom.
If the calculated value of 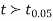 the difference between the sample means is said to be significant at 5% level of significance.
the difference between the sample means is said to be significant at 5% level of significance.
If 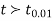 , the difference is said to be significant at 1% level of significance.
, the difference is said to be significant at 1% level of significance.
If 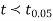 , the data is said to be consistent with the hypothesis, that
, the data is said to be consistent with the hypothesis, that 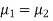
Cor. If the two samples are of the same size and the data are paired, then t is defined by
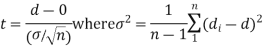
Example. From a random sample of 10 pigs fed on diet A. The increase in weight in a certain period were 10, 6, 16, 17, 13, 12, 8, 14, 15, 9 lbs. For another random sample of 12 pig’s fat on diet B, the increases in the same period were 7, 13, 22, 15, 12, 14, 18, 8, 21, 23, 10, 17 lbs. Test whether diets A and B differ significantly as regards their effects on increases in weight?
Solution. We calculate the means and standard deviation of the samples as follows
| Diet A |
|
| Diet B |
|
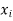 | 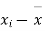 |  | 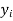 | 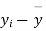 | 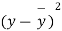 |
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 18 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 23 | 2 | 4 |
120 | 0 | 120 | 10 | 0 | 314 |

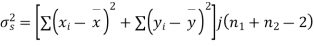
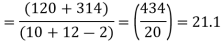
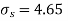
Assuming that the samples do not differ in weight so far as two diets are concerned i.e. 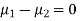
Hence, 
Here, 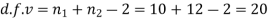
For 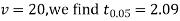
The calculated value of 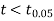
Hence the difference between the sample means is not significant that is the two diets do not differ significantly as regards their effects on increase in weight.
Test for Single Mean
When you test a single mean, you’re comparing the mean value to some other hypothesized value. Which test you run depends on if you know the population standard deviation (σ) or not.
Known population standard deviation
If you know the value for σ, then the population mean has a normal distribution: use a one sample z-test. The z-test uses a formula to find a z-score, which you compare against a critical value found in a z-table. The formula is:
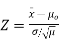
A one sample test of means compares the mean of a sample to a pre-specified value and tests for a deviation from that value. For example we might know that the average birth weight for white babies in the US is 3,410 grams and wish to compare the average birth weight of a sample of black babies to this value.
Assumptions
- Independent observations.
- The population from which the data is sampled is normally distributed.
Hypothesis:
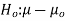
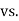
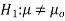
Where μ0 is a pre-specified value (in our case this would be 3,410 grams).
Test Statistic
- First calculate
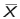 , the sample mean.
, the sample mean. - We choose an α = 0.05 significance level
- If the standard deviation is known:
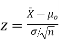
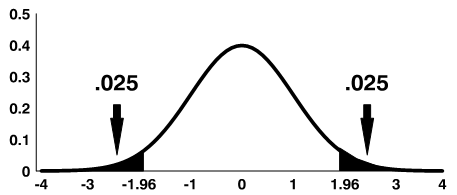
Using the significance level of 0.05, we reject the null hypothesis if z is greater than 1.96 or less than -1.96.
- If the standard deviation is unknown:
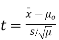
Using the significance level of 0.05, we reject the null hypothesis if |t| is greater than the critical value from a t-distribution with df = n-1.
Note: The shaded area is referred to as the critical region or rejection region.
We can also calculate a 95% confidence interval around the mean. The general form for a confidence interval around the mean, if σ is unknown, is
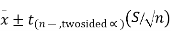
For a two-sided 95% confidence interval, use the table of the t-distribution (found at the end of the section) to select the appropriate critical value of t for the two-sided α=0.05.
Example: one sample t-test
Recall the data used in module 3 in the data file "dixonmassey."
Data dixonmassey;
Input Obs chol52 chol62 age cor dchol agelt50 $;
Datalines;
1 | 240 | 209 | 35 | 0 | -31 | y |
2 | 243 | 209 | 64 | 1 | -34 | n |
3 | 250 | 173 | 61 | 0 | -77 | n |
4 | 254 | 165 | 44 | 0 | -89 | y |
5 | 264 | 239 | 30 | 0 | -25 | y |
6 | 279 | 270 | 41 | 0 | -9 | y |
7 | 284 | 274 | 31 | 0 | -10 | y |
8 | 285 | 254 | 48 | 1 | -31 | y |
9 | 290 | 223 | 35 | 0 | -67 | y |
10 | 298 | 209 | 44 | 0 | -89 | y |
11 | 302 | 219 | 51 | 1 | -83 | n |
12 | 310 | 281 | 52 | 0 | -29 | n |
13 | 312 | 251 | 37 | 1 | -61 | y |
14 | 315 | 208 | 61 | 1 | -107 | n |
15 | 322 | 227 | 44 | 1 | -95 | y |
16 | 337 | 269 | 52 | 0 | -68 | n |
17 | 348 | 299 | 31 | 0 | -49 | y |
18 | 384 | 238 | 58 | 0 | =146 | n |
19 | 386 | 285 | 33 | 0 | -101 | y |
20 | 520 | 325 | 40 | 1 | -195 | y |
;
Many doctors recommend having a total cholesterol level below 200 mg/dl. We will test to see if the 1952 population from which the Dixon and Massey sample was gathered is statistically different, on average, from this recommended level.
- H0: μ = 200 vs. H1: μ ≠ 200
- α=0.05
- Our sample of n=20 has
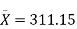 = 311.15 and s = 64.3929.
= 311.15 and s = 64.3929. - Df = 19, so reject H0 if |t| > 2.093
Calculate:
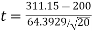
|t| > 2.093 so we reject H0
The 95% confidence limits around the mean are
311.15 ± (2.093)(64.3929/√20)
311.15 ± 30.14
(281.01, 341.29)
One Sample t-test Using SAS:
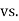
Proc ttest data=name h0=μ0 alpha=α;
Var var;
Run;
SAS uses the stated α for the level of confidence (for example, α=0.05 will result in 95% confidence limits). For the hypothesis test, however, it does not compute critical values associated with the given α, and compare the t-statistic to the critical value. Rather, SAS will provide the p-value, the probability that T is more extreme than observed t. The decision rule, "reject if |t| > critical value associated with α" is equivalent to "reject if p < α."
SAS will provide the p value, the probability that T is more extreme than observed t. The decision rule, “reject if |t| critical value associated with
critical value associated with 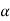 ” is equivalent to “reject if p
” is equivalent to “reject if p 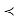 a.”
a.”
Example:
Proc ttest data=dixonmassey h0=200 alpha=0.05;
Var chol52;
Title 'One Sample t-test with proc ttest';
Title2 'Testing if the sample of cholesterol levels in 1952 is statistically different from 200' ;
Run;
One sample t-test with proc ttest
‘Testing if the sample of cholesterol level in 1952 is statistically different from
The T TEST Procedure
Variable : chol52
N | Mean | Std Dev | Std Err | Minimum | Maximum |
20 | 311.2 | 64.3929 | 14.3987 | 240.0 | 520.0 |
Mean | 95% CL Mean | Std Dev | 95% CL | Std Dev |
311.2 | 281.0 | 64.3929 | 48.9702 | 94.0505 |
DF | T Value | Pr> |t| |
19 | 7.72 | <.0001 |
As in our hand calculations, t = 7.72, and we reject H0 (because p<0.0001 which is < 0.05, our selected α level).
The mean cholesterol in 1952 was 311.2, with 95% confidence limits (281.0, 341.3).
Difference of Means and Correlation Coefficients
Testing the meaning of the correlation coefficient.
The relationship coefficient, r, tells us about the strength and direction of the linear relationship between X1 and X2.
Sample data is used to calculate r, the correlation coefficient for the sample. If we had data for the entire population, we could find the correlation coefficient for the population.
But since we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r, is our estimate of the correlation coefficient for the unknown population.
• ρ = population correlation coefficient (unknown)
• r = sample relationship coefficient (known; calculated from sample data)
The hypothesis test allows us to decide if the value of the population correlation coefficient ρ is "close to zero" or "significantly different from zero". We decide on the basis of the correlation coefficient of sample r and the size of sample n.
If the test arranges that the relationship coefficient is meaningfully different from zero, we say that the relationship coefficient is "significant".
• Conclusion: there is sufficient evidence to conclude that there is a significant linear relationship between X1 and X2 because the correlation coefficient is significantly different from zero.
• Meaning of the conclusion: there is a significant linear relationship X1 and X2. If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that the correlation coefficient is not "significant".
Take the hypothesis test
• Null hypothesis: H0: ρ = 0
• Alternative hypothesis: Ha: ρ≠ 0
What do hypotheses mean in words?
• Hypothesis H0: the population correlation coefficient is NOT meaningfullydissimilar from zero. There is NO significant linear relationship (correlation) between X1 and X2 in the population.
• Alternative hypothesis Ha: the population correlation coefficient is significantly different from zero. Here is a significant linear relationship (correlation) amid X1 and X2 in the population.
Drawing a conclusion There are two methods of making a hypothetical decision. The test statistic to test this hypothesis is:
When the second formula is an equivalent form of the test statistic, n is the sample size and the degrees of freedom are n-2. This is a t-statistic and works in the same way as other t-tests.
Calculate the value t and compare it to the critical value in table t at the appropriate degrees of freedom and the level of confidence you want to maintain. If the calculated value is in the queue, then you cannot accept the null hypothesis that there is no linear relationship between these two independent random variables.
If the calculated t value is NOT in the queue, it is not possible to reject the null hypothesis that there is no linear relationship between the two variables.
A quick way to test correlations is the relationship between sample size and correlation. Me:
Then this implies that the correlation between the two variables demonstrates the existence of a linear relationship and is statistically significant at approximately the significance level of 0.05.
As the formula indicates, there is an inverse relationship between the sample size and the required correlation for the meaning of a linear relationship.
With only 10 observations, the required correlation for significance is 0.6325, for 30 observations the required correlation for significance drops to 0.3651 and for 100 observations the required level is only 0.2000.
Correlations can be useful for visualizing data, but are not used appropriately to "explain" a relationship between two variables. Perhaps a single statistic is not used more inadequately than the correlation coefficient.
Quoting correlations between health conditions and anything from place of residence to eye color has the effect of implying a cause and effect relationship. This simply cannot be accomplished with a correlation coefficient.
The correlation coefficient is obviously innocent of this misinterpretation. The analyst has a duty to use a statistic designed to test cause and effect relationships and report those results only if he intends to submit such a request.
The problem is that passing this stricter test is difficult, so lazy and / or unscrupulous "investigators" turn to correlations when they cannot legitimately support their case.
Define a t-test of a regression coefficient and provide a unique example of its use. Definition: A t-test is obtained by dividing a regression coefficient by its standard error and then comparing the result with critical values for students with df error.
Provides a test for the claim that when all other variables were included in the relevant regression model. Example: Suppose that 4 variables are suspected to influence some response. Suppose the assembly results include:
Variable | Regression coefficient | Standard error of regular coefficient |
.5 | 1 | -3 |
.4 | 2 | +2 |
.02 | 3 | +1 |
.6 | 4 | -.5 |
- t calculated for variables 1, 2 and 3 would be 5 or greater in absolute value while for variable 4 it would be less than 1. For most levels of significance, the hypothesis would be rejected. However, note that this is the case where, and have been included in the regression. For most levels of significance, the hypothesis would have continued (held) for the case where, and are in regression. Often this pattern of results will involve calculating another regression involving only and examining the proportions produced for that case.
- The correlation between the scores on a neuroticism test and the scores on an anxiety test is high and positive; Thus
- To. Anxiety causes neuroticism
- Yes. Those who score low on one test tend to score high on the other.
- C. Those who score small on one test tend to score low on the other.
- Re. You cannot make a meaningful prediction from one test to another.
- C. Those who score small on one test tend to score low on the additional.
- Testing the meaning of the correlation coefficient.
- LEARNING OUTCOMES
- • Calculate and interpret the correlation coefficient.
- The correlation coefficient, r, says us about the asset and direction of the linear relationship amid x and y. However, the reliability of the linear model also depends on the number of data points observed in the sample. We have to examine together the value of the correlation coefficient r and the sample size n.
- We done a hypothesis test on the "significance of the correlation coefficient" to choose whether the linear relationship in the sample data is strong sufficient to be used to model the connection in the population.
- Sample data is used to calculate r, the correlation coefficient for the sample. If we had data for the entire population, we could find the correlation coefficient for the population. But since we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r, is our estimate of the correlation coefficient for the unknown population.
- • The representation for the population correlation coefficient is ρ, the Greek letter "rho".
- ρ = population correlation coefficient (unknown)
- r = sample correlation coefficient (known; calculated from sample data)
- The hypothesis test allows us to decide if the value of the population correlation coefficient
- ρ is "near to zero" or "significantly dissimilar from zero". We decide on the basis of the correlation coefficient of sample r and the size of sample n.
- If the test determines that the correlation coefficient is meaningfullydissimilar from zero, we say that the association coefficient is "significant".
- Assumption: there is sufficient indication to accomplish that there is aimportant linear relationship between x and y, since the association coefficient is significantly dissimilar from zero. What does the conclusion mean: There is a significant linear relationship between x and y. We can practice the reversion line to model the linear relationship amid x and y in the population.
- If the test achieves that the correlation coefficient is not meaningfullydiverse from zero (it is close to zero), we say that the correlation coefficient is not "significant".
- Assumption: “There is insufficient indication to accomplish that there is a significant linear relationship amid
- x and y because the correlation coefficient is not meaningfullydissimilar from zero. "What the conclusion means: There is no important linear association between x and y. So, we CANNOT use the reversion line to model a linear relationship amid x and y in the population.
- Note
- • If r is significant and the scatter diagram shows a linear trend, the line can be used to predict the value of y for the values of x that fall within the domain of the observed values of x.
- • If r is not significant OR if the scatter diagram does not show a linear trend, the line should not be used for forecasting.
- • If r is significant and if the scatter diagram shows a linear trend, the line may NOT be appropriate or reliable to predict OUT of the domain of the x values observed in the data.
- Take the hypothesis test
- Null hypothesis: H0: ρ = 0
- Alternative hypothesis: Ha: ρ≠ 0
- What do hypotheses mean in words?
- Hypothesis H0: the population relationship coefficient is NOT meaningfullydissimilar from zero. There is NO significant linear relationship (correlation) between x and y in the population.
- Alternative hypothesis Ha: the population correlation coefficient is significantly different from zero. There is aimportant linear relationship (correlation) between x and y in the population.
- Get a conclusion
- There are two methods of making the decision. The two methods are equivalent and give the same result.
- Method 1: using the p value
- Method 2: use of a table of critical values.
- In this chapter of this textbook, we will continuously use a significance level of 5%, α = 0.05
Note
- Using the p-value method, you can choose any appropriate level of significance desired; It is not limited to the use of α = 0.05. But the critical value table provided in this textbook assumes that we are using a significance level of 5%, α = 0.05. (If we wanted to use a significance level other than 5% with the critical value method, we would need several tables of critical values that are not provided in this manual).
- Method 1: use a p-value to make a decision
- To calculate the p-value using LinRegTTEST:
- • On the LinRegTTEST input screen, at the line prompt for β or ρ, highlight "≠ 0"
- The output screen shows the p value on the line that says "p =".
- (Most statistical software can calculate the p-value).
- If the p value is fewer than the meaning level (α = 0.05)
- Decision: reject the null hypothesis.
- Assumption: "There is sufficient indication to accomplish that there is aimportant linear relationship amid x and y since the correlation coefficient is meaningfullydissimilar from zero."
- If the p value is NOT less than the meaning level (α = 0.05)
- Decision: DO NOT reject the null hypothesis.
- Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is NOT significantly different from zero."
- Calculation Notes:
- Use technology to calculate the p-value. The calculations for calculating test statistics and p-value are described below:
- The p-value is considered using a t-distribution with n - 2 degrees of freedom.
- The formula for the test statistic is t = r√n - 2√1 - r2t = rn - 21 - r2. The test statistic value, t, is displayed on the computer or calculator output along with the p-value. The t-test statistic has the same sign as the correlation coefficient r.
- The p-value is the combined area in both tails.
(1) CHI SQUARE 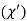 TEST
TEST
When a fair coin is tossed 80 times we expect from the theoretical considerations that heads will appear 40 times and tail 40 times. But this never happens in practice that is the results obtained in an experiment do not agree exactly with the theoretical results. The magnitude of discrepancy between observations and theory is given by the quantity 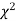 (pronounced as chi squares). If
(pronounced as chi squares). If 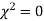 the observed and theoretical frequencies completely agree. As the value of
the observed and theoretical frequencies completely agree. As the value of 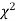 increases, the discrepancy between the observed and theoretical frequencies increases.
increases, the discrepancy between the observed and theoretical frequencies increases.
(1) Definition. If  and
and  be the corresponding set of expected (theoretical) frequencies, then
be the corresponding set of expected (theoretical) frequencies, then 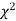 is defined by the relation
is defined by the relation
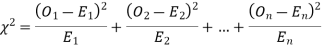

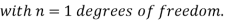
(2) Chi – square distribution
If 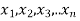 be n independent normal variates with mean zero and s.d. Unity, then it can be shown that
be n independent normal variates with mean zero and s.d. Unity, then it can be shown that 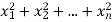 is a random variate having
is a random variate having 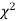 distribution with ndf.
distribution with ndf.
The equation of the 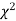 curve is
curve is
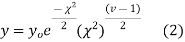
(3) Properties of 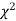 distribution
distribution
- If v = 1, the
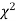 curve (2) reduces to
curve (2) reduces to 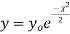 which is the exponential distribution.
which is the exponential distribution. - If
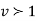 this curve is tangential to x – axis at the origin and is positively skewed as the mean is at v and mode at v-2.
this curve is tangential to x – axis at the origin and is positively skewed as the mean is at v and mode at v-2. - The probability P that the value of
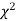 from a random sample will exceed
from a random sample will exceed 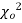 is given by
is given by
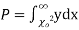
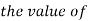
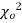 have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)
have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)
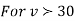 ,the
,the  curve approximates to the normal curve and we should refer to normal distribution tables for significant values of
curve approximates to the normal curve and we should refer to normal distribution tables for significant values of 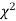 .
.
IV. Since the equation of 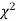 curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
V. Mean = 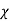 and variance =
and variance = 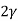
Goodness of fit
The values of 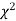 is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit given distribution
is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit given distribution 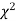 therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory and fact.
therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory and fact.
This is a nonparametric distribution free test since in this we make no assumptions about the distribution of the parent population.
Procedure to test significance and goodness of fit
(i) Set up a null hypothesis and calculate
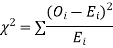
(ii) Find the df and read the corresponding values of  at a prescribed significance level from table V.
at a prescribed significance level from table V.
(iii) From 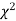 table, we can also find the probability P corresponding to the calculated values of
table, we can also find the probability P corresponding to the calculated values of 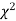 for the given d.f.
for the given d.f.
(iv) If P<0.05, the observed value of 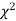 is significant at 5% level of significance
is significant at 5% level of significance
If P<0.01 the value is significant at 1% level.
If P>0.05, it is a good faith and the value is not significant.
Example. A set of five similar coins is tossed 320 times and the result is
Number of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
Solution. For v = 5, we have 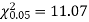
P, probability of getting a head=1/2;q, probability of getting a tail=1/2.
Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion 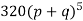
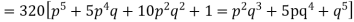
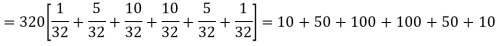
Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.
Hence, 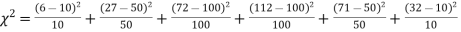
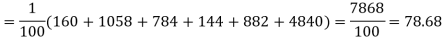
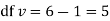
Since the calculated value of 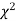 is much greater than
is much greater than 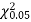 the hypothesis that the data follow the binomial law is rejected.
the hypothesis that the data follow the binomial law is rejected.
Example. Fit a Poisson distribution to the following data and test for its goodness of fit at level of significance 0.05.
x | 0 | 1 | 2 | 3 | 4 |
f | 419 | 352 | 154 | 56 | 19 |
Solution. Mean m =
Hence, the theoretical frequency are 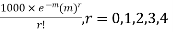
x | 0 | 1 | 2 | 3 | 4 | Total |
f | 404.9 (406.2) | 366 | 165.4 | 49.8 | 11..3 (12.6) | 997.4 |
Hence, 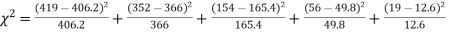
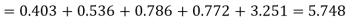
Since the mean of the theoretical distribution has been estimated from the given data and the totals have been made to agree, there are two constraints so that the number of degrees of freedom v = 5- 2=3
For v = 3, we have 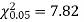
Since the calculated value of 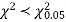 the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
Example. In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
Solution. The corresponding frequencies are

Hence, 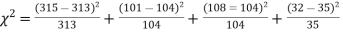

For v = 3, we have 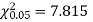
Since the calculated value of 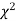 is much less than
is much less than  there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.