Unit–1

Random variable and discrete probability distributions

1.1. Conditional probability

Let A and B be two events of a sample space Sand let 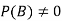. Then conditional probability of the event A, given B, denoted by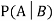is defined by –

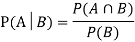
Theorem: If the events A and B defined on a sample space S of a random experiment are independent, then

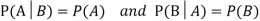
Example1: A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.

SOLUTION: We consider the following events:

A: Selected item comes from A.

B: Selected item comes from B.

D: Selected item is defective.

We are looking for 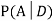. We know:

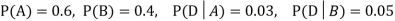
Now,

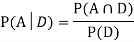
So we need

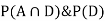
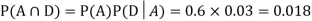
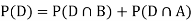
Since, D is the union of the mutually exclusive events 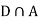and 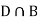(the entire sample space is the union of the mutually exclusive events A and B)

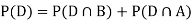
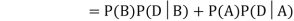
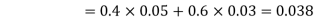
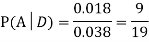
Example: Two fair dice are rolled, 1 red and 1 blue. The Sample Space is

S = {(1, 1),(1, 2), . . . ,(1, 6), . . . ,(6, 6)}.Total -36 outcomes, all equally likely (here (2, 3) denotes the outcome where the red die show 2 and the blue one shows 3).

(a) Consider the following events:

A: Red die shows 6.

B: Blue die shows 6.

Find 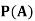 , 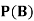and .

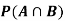Solution: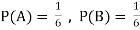

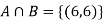
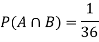
NOTE: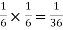so 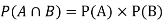for this example. This is not surprising - we expect A to occur in of cases. In of these cases i.e. in 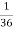of all cases, we expect B to also occur.

(b) Consider the following events:

C: Total Score is 10.

D: Red die shows an even number.

Find 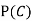, 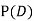and .

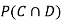Solution: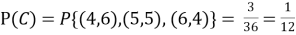

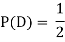
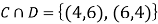
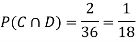
NOTE: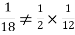so,.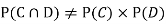

Why does multiplication not apply here as in part (a)?

ANSWER: Suppose C occurs: so the outcome is either (4, 6), (5, 5) or (6, 4). In two of these cases, namely (4, 6) and (6, 4), the event D also occurs. Thus

Although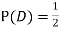 , the probability that D occurs given that C occurs is .

We write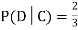, and call 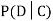the conditional probability of D given C.

NOTE: In the above example

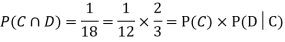
Example: Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball drawn is red find the probability that it is drawn from the first urn.

Solution:

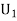:The ball is drawn from urnI.

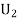: The ball is drawn from urnII.

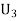: The ball is drawn from urnIII.

R:The ball is red.

We have to find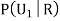

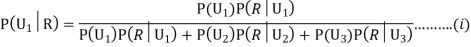
Since the three urns are equally likely to be selected

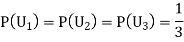
Also,

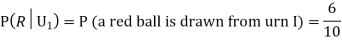
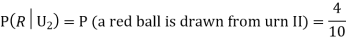
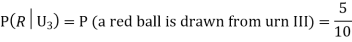
From (i), we have

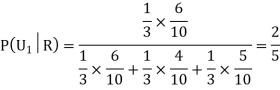
Example: A bag contains 12 pens of which 4 are defective. Three pens are picked at random from the bag one after the other.

Then find the probability that all three are non-defective.

Sol. Here the probability of the first which will be non-defective = 8/12

By the multiplication theorem of probability,

If we draw pens one after the other then the required probability will be-

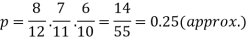
Example: The probability of A hits the target is 1 / 4 and the probability that B hits the target is 2/ 5. If both shoot the target then find the probability that at least one of them hits the target.

Sol.

Here it is given that-

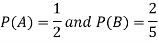
Now we have to find-

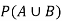
Both two events are independent. So that-

1.2. Probability spaces

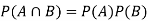
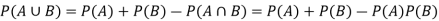
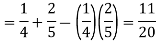
A probability space is a three-tuple (S, F, P) in which the three components are

1. Sample space: A non-empty set S called the sample space, which represents all possible outcomes.
2. Event space: A collection F of subsets of S, called the event space.
3. Probability function: A function P : FR, that assigns probabilities to the events in F.

DEFINITIONS:

1. Die: It is a small cube. Dots (number) are marked on its faces. Plural of the die is dice. On throwing a die, the outcome is the number of dots on its upper face.

2. Cards: A pack of cards consists of four suits i.e. Spades, Hearts, Diamonds and Clubs. Each suit consists of 13 cards, nine cards numbered 2, 3, 4, ..., 10, an Ace, a King, a Queen and a Jack or Knave. Colour of Spades and Clubs is black and that of Hearts and Diamonds is red.

Kings, Queens and Jacks are known as face cards.

3. Exhaustive Events or Sample Space: The set of all possible outcomes of a single performance of an experiment is exhaustive events or sample space. Each outcome is called a sample point.

In case of tossing a coin once, S = (H, T) is the sample space. Two outcomes - Head and Tail

- constitute an exhaustive event because no other outcome is possible.

4. Random Experiment: There are experiments, in which results may be altogether different, even though they are performed under identical conditions. They are known as random experiments. Tossing a coin or throwing a die is random experiment.

5. Trial and Event: Performing a random experiment is called a trial and outcome is termed as event. Tossing of a coin is a trial and the turning up of head or tail is an event.

6. Equally likely events: Two events are said to be ‘equally likely’, if one of them cannot be expected in preference to the other. For instance, if we draw a card from well-shuffled pack, we may get any card. Then the 52 different cases are equally likely.

7. Independent events: Two events may be independent, when the actual happening of one does not influence in any way the probability of the happening of the other.

8. Mutually Exclusive events: Two events are known as mutually exclusive, when the occurrence of one of them excludes the occurrence of the other. For example, on tossing of a coin, either we get head or tail, but not both.

9. Compound Event: When two or more events occur in composition with each other, the simultaneous occurrence is called a compound event. When a die is thrown, getting a 5 or 6 is a compound event.

10. Favourable Events: The events, which ensure the required happening, are said to be favourable events. For example, in throwing a die, to have the even numbers, 2, 4 and 6 are favourable cases.

11. Conditional Probability: The probability of happening an event A, such that event B has already happened, is called the conditional probability of happening of A on the condition that B has already happened. It is usually denoted by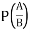

12. Odds in favour of an event and odds against an event: If number of favourable ways = m, number of not favourable events = n

(i) Odds in favour of the event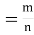

(ii) Odds against the event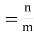

13. Classical Definition of Probability. If there are N equally likely, mutually, exclusive and exhaustive of events of an experiment and m of these are favourable, then the probability of the happening of the event is defined as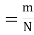

Consider Example1: In poker, a full house (3 cards of one rank and two of another, e.g. 3 fours and 2 queens) beats a flush (five cards of the same suit).

A player is more likely to be dealt a flush than a full house. We will be able to precisely quantify the meaning of “more likely” here.

Example2: A coin is tossed repeatedly.

Each toss has two possible outcomes:

Heads (H) or Tails (T)

Both equally likely. The outcome of each toss is unpredictable; so is the sequence of H and T.

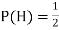However, as the number of tosses gets large, we expect that the number of H (heads) recorded will fluctuate around of the total number of tosses. We say the probability of aH is , abbreviated by . Of course  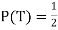 also

Example3:

If 4 coins are tossed, what is the probability of getting 3 heads and 1 tail?

NOTES:

• In general, an event has associated to it a probability, which is a real number between 0 and 1.

• Events which are unlikely have low (close to 0) probability, and events which are likely have high (close to 1) probability.

• The probability of an event which is certain to occur is 1; the probability of an impossible event is 0.

Probability-

Let S be a sample space, and each outcome of an experiment is equally likely and the number of outcomes is finite.

If A is an event connected with the experiment, then the probability of occurrence of event A is given by-

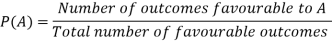
Example: If a card is selected from the pack of playing cards then what will be the probability of the following cases?

1. A = {the card is a diamond}

2. B = {the card is a face card}

Sol.

As we know that-

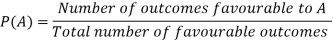
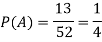
And \

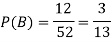
Note-

1. The probability of an event lies between 0 to 1, i.e.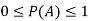

2. If events A and B are mutually exclusive then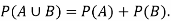

3. Let A be any event then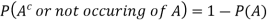

4. The sum of all probabilities in the sample space is 1.

5. The probability of an event which can not occur is 0.

Addition rule of probability-

For any events A and B,

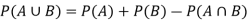
Example: In a college counselling, 30 students are choosing maths, 20 are choosing Computer science and 10 are selecting maths and computer science.

Suppose a student is selected randomly from 100 students then find the probability that student choose maths or computer science.

Sol.

Let A = {student is taking maths} and B = {student taking computer science}

So that the probabilities will be-

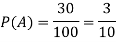
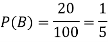
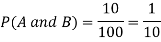
Hence by the addition principle of probability-

1.3. Discrete random variables, Independent random variables

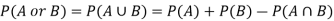
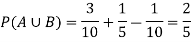
Independence:

Two events A, B ∈ are statistically independent iff

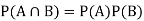
(Two disjoint events are not independent.)

Independence implies that

Knowing that outcome is in B does not change your perception of the outcome’s being in A.

Random Variable: It is a real valued function which assign a real number to each sample point in the sample space.

Random Variables

A random variable X is a function defined on the sample space 5 of an experiment S of an experiment. Its value are real numbers. For every number a the probability

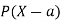
With which X assumes a is defined. Similarly for any interval l the probability

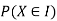
With which X assumes any value in I is defined.

Example: 1.Tossing a fair coin thrice then-

Sample Space(S) = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

2. Roll a dice

Sample Space(S) = {1,2,3,4,5,6}

Discrete Random Variable:

A random variable is said to be discrete if it has either a finite or a countable number of values

The number of students present each day in a class during an academic session is an example of discrete random variable as the number cannot take a fractional value.

Discrete Random Variables and Distribution

By definition a random variable X and its distribution are discrete if X assumes only finitely maany or at most contably many values 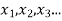called the possible values of X. With positive probabilities 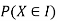is zero for any interval J containing no possible values.

Clearly the discrete distribution of X is also determined by the probability functions f (x) of X, defined by

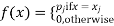
From this we get the values of the distribution function F (x) by taking sums.

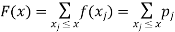
Example: 1. No. Of head obtained when two coin are tossed.

2. No. Of defective items in a lot.

Probability mass function-

Let X be a r.v. Which takes the values 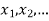and let P[X = 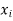] = p(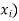. This function p(xi), i =1,2, … defined for the values 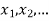assumed by X is called probability mass function of X satisfying p(xi) ≥ 0 and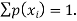

Example: A random variable x has the following probability distribution-

Then find-

1. Value of c.

2. P[X≤3]

3. P[1 < X <4]

Sol.

We know that for the given probability distribution-

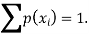
So that-

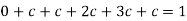
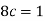
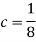
2.

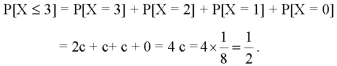
3.

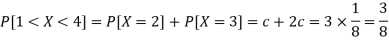
Independent random variables-

Two discrete random variables X and Y are said to be independent only if-

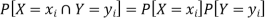
Note- Two events are independent only if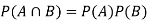

Example: Two discrete random variables X and Y have-

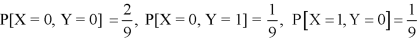
And

P[X = 1, Y = 1] = 5/9.

Check whether X and Y are independent or not?

Sol.

First we write the given distribution In tabular form-

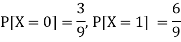
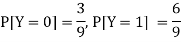
Now-

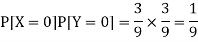
But

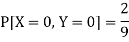
So that-

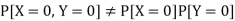
Hence X and Y are not independent.

1.4. Expectation of discrete random variables, Sums of independent random variables

Let a random variable X has a probability distribution which assumes the values say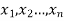 with their associated probabilities 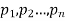then the mathematical expectation can be defined as-

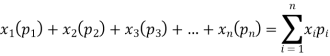
The expected value of a random variable X is written as E(X).

Expected value for a continuous random variable is

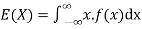
OR

The mean value (μ) of the probability distribution of a variate X is commonly known as its expectation current is denoted by E (X). If f(x) is the probability density function of the variate X, then

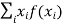                              (discrete distribution)

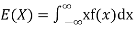                (continuous distribution)

In general expectation of any function is 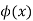given by

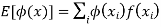         (discrete distribution)

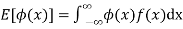      (continuous distribution)

(2) Variance offer distribution is given by

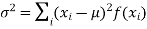             (discrete distribution)

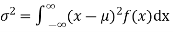           (continuous distribution)

Where 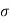is the standard deviation of the distribution.

(3) The rth moment about mean (denoted by 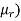is defined by

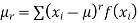                    (discrete function)

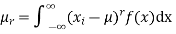               (continuous function)

(4) Mean deviation from the mean is given by

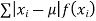                                 (discrete distribution)

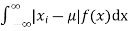                        (continuous distribution)

Example. In a lottery, m tickets are drawn at a time out of a tickets numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.

Solution. Let 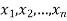be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have

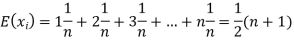
Therefore expected value of the sum of the numbers on the tickets drawn

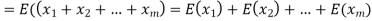
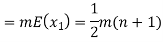
Example. X is a continuous random variable with probability density function given by

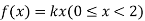
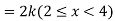
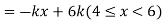
Find k and mean value of X.

Solution. Since the total probability is unity.

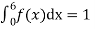
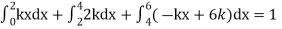
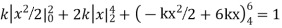
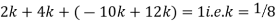
Mean of X =

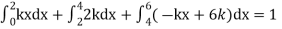
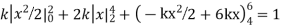
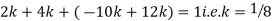
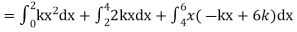
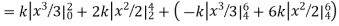
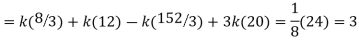
Example. The frequency distribution of a measurable characteristic varying between 0 and 2 is as under

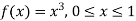
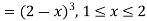
Calculate two standard deviation and also the mean deviation about the mean.

Solution. Total frequency N =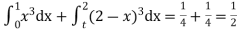

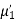(about the origin)=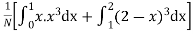

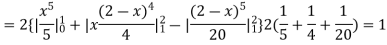
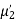(about the origin)=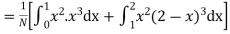

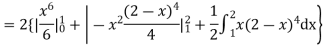
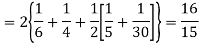
Hence,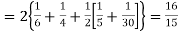

i.e., standard deviation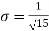

Mean derivation about the mean

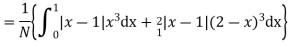
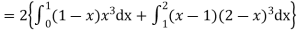
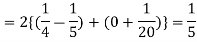
Example: If a random variable X has the following probability distribution in tabular form then what will be the expected value of X.

Sol.

We know that-

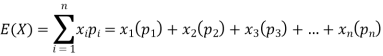
So that-

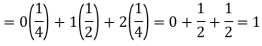
Example: Find the expectations of the number of an unbiased die when thrown.

Sol. Let X be a random variable which represents the number on a die when thrown.

X can take the values-

1, 2, 3, 4, 5, 6

With

P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6

The distribution table will be-

Hence the expectation of number on the die thrown is-

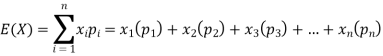
So that-

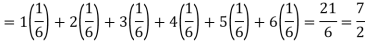
Independent random variables

In real life, we usually need to deal with more than one random variable. For example, if you study physical characteristics of people in a certain area you might pick a person at random and then look at his/ her weight, height etc. the weight of the randomly chosen person is one random variable while his/ her height is another one. Not only do we need to study is random variable separately but also we need to consider if there is dependence (i.e. correlation) between them. Is it true that a taller person is more likely to be heavier or not? the issues of dependence between several random variables will be studied in detail later on, but here we would like to talk about special scenario where two random variables are independent.

The concept of independent random variables is very similar to independent events. Remember to A and B are independent if we have P (A,B) = P (A) P (B) (remember comma means and, i.e. P(A,B) = P (A and B) = P (A 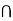B). Similarly we have the following definition for independent discrete random variables.

Definition

Consider two discrete random variables X and Y. We say that X and Y are independent if

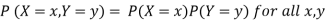
In general if two random variables are independent then you can write

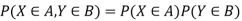, For all sets A and B

Definition

Consider n discrete random variables 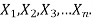We say that 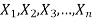are independent if

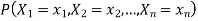
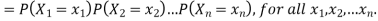
Example.

I toss a coin twice and define X to be the number of heads one observe. Then I toss the coin two more times and define Y to be the number of heads that I observed this time. Find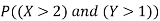

Solution. since X and Y are the result of different independent coin tosses the two random variables X and Y are independent.

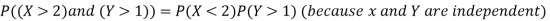
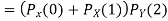
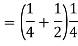
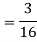
Example. A box A contains 2 white and 4 Black balls. Another box B contains 5 white and 7 black balls. A ball is transferred from the box A to the box B. Then A ball is drawn from the box B. Find the probability that it is white.

Solution. The probability of drawing a white ball from box B will depend on whether the transferred ball is black or white.

If black ball is transferred, it's probability is 4/6. There are now 5 white and 8 black balls in the box B.

Then the probability of drawing a white ball from box B is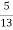

Thus the probability of drawing a white ball from B, if the transferred ball is black

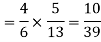
Similarly the probability of drawing a white ball from urn B if the transferred ball is white

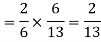
Hens required probability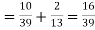

Example. A pair of dice is tossed twice. Find the probability of scoring 7 points

(a)  Once

(b) At least once

(c)  Twice

Solution. In a single toss of two dice the sum 7 can be obtained as (1,6), (2,5), (3,4), (4,3), (5,2), (6,1), i.e. in 6 ways so that the probability of getting 7 = 6/36 = 1/6

Also the probability of not getting 7 = 1-1/6= 5/6

(a)  The probability of getting seven in the first toss and not getting 7 in the second toss=1/6×5/6=5/36

Similarly the probability off not getting seven in the first toss and getting 7:00 in the second toss=5/6×1/6=5/36

Since these mutually exclusive events addition law of probability applies

Required probability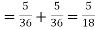

(b) The probability of not getting 7 in either toss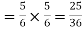

Therefore the probability of getting 7 at least once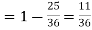

(c)  The probability of getting 7 twice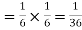

Example. Two cards are drawn in succession from a pack of 52 cards. Find the chance that the first is a king and the second a queen if the first card is

(i)                Replaced

(ii)              Got replaced

Solution. (i) the probability of drawing a king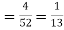

If the card is replaced the back will again have 52 cards so that the probability of drawing a queen is 1/13.

The two events being independent the probability of drawing both cards in succession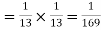

(ii)the probability of drawing a king = 1/13

If the card is not replaced the pack will have 51 cards only so that the chance of drawing the queen is 4/51.

Hence the probability of drawing both cards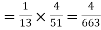

Example. Two cards are selected at random from 10 cards numbered 1to10 find the probability p that the sum is odd if

(i)                The two cards are drawn together

(ii)              the two cards are drawn one after the other without replacement

(iii)           The two cards are drawn one after the other with replacement

Solution. (i) two cars out of 10 can be selected in 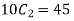ways. The sum is odd if one number is odd and other number is even. There being 5 odd numbers (1,3,5,7,9) and 5 even numbers (2,4,6,8,10) an what and an even number is chosen in 5×5=25 ways.

Thus,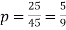

(ii)two cards out of 10 can be selected one of the other without replacing in 10 × 10 = 100 ways

An odd number is selected in 5 × 5 =25 ways and an even number in 5 × 5 = 25 ways

Thus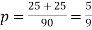

(iii)two cards can be selected one after the other with replacement in 10 × 10 =100 ways

An odd number is selected in 5 × 5 =25 ways and an even number in 5×5=25 ways

Thus,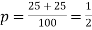

1.5. Moments, Variance of a sum, Correlation coefficient

Moments-

The r’th moment of a variable x about the mean is denoted by 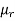and defined as-

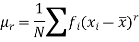
The r’th moment of a variable x about any point ‘a’ will be-

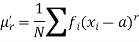
Relationship between moments about mean and moment about any point-

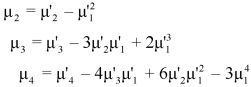
When two variables are related in such a way that change in the value of one variable affects the value of the other variable, then these two variables are said to be correlated and there is correlation between two variables.

Example- Height and weight of the persons of a group.

The correlation is said to be perfect correlation if two variables vary in such a way that their ratio is constant always.

Variance of a sum

One of the applications of covariance is finding the variance of a sum of several random variables. In particular, if Z = X + Y, then

Var (Z) =Cov (Z,Z)

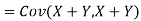
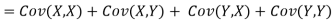
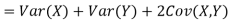
More generally, for a, b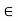R we conclude

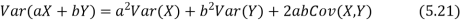
Variance

Consider two random variables X and Y with the following PMFs

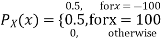                      (3.3)

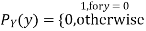                           (3.4)

Note that EX =EY = 0. Although both random variables have the same mean value, their distribution is completely different. Y is always equal to its mean of 0, while X is IDA 100 or -100, quite far from its mean value. The variance is a measure of how spread out the distribution of a random variable is. Here the variance of Y is quite small since its distribution is concentrated value. Why the variance of X will be larger since its distribution is more spread out.

The variance of a random variable X with mean 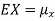, is defined as

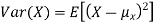
By definition the variance of X is the average value of 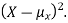Since 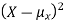≥0, the variance is always larger than or equal to zero. A large value of the variance means that 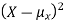is often large, so X often X value far from its mean. This means that the distribution is very spread out. On the other hand a low variance means that the distribution is concentrated around its average.

Note that if we did not square the difference between X and its mean the result would be zero. That is

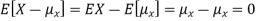
X is sometimes below its average and sometimes above its average. Thus 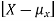is sometimes negative and sometimes positive but on average it is zero.

To compute 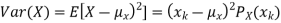, note that we need to find the expected value of 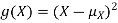, so we can use LOTUS. In particular we can write

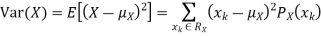
For example, for X and Y defined in equations 3.3 and 3.4 we have

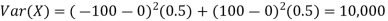
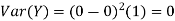
As we expect, X has a very large variance while Var (Y) = 0

Note that Var (X) has a different unit than X. For example, if X is measured in metres then Var(X) is in 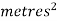.to solve this issue we define another measure called the standard deviation usually shown as 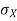which is simply the square root of variance.

The standard deviation of a random variable X is defined as

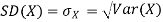
The standard deviation of X has the same unit as X. For X and Y defined in equations 3.3 and 3.4 we have

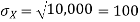
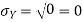
Here is a useful formula for computing the variance.

Computational formula for the variance

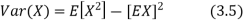
To prove it note that

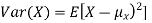
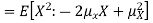
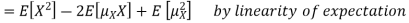
Note that for a given random variable X, 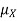is just a constant real number. Thus 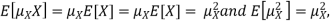so we have

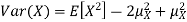
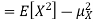
Equation 3.5 is equally easier to work with compared to 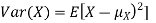. To use this equation we can find 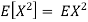using LOTUS.

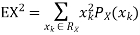
And then subtract 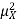to obtain the variance.

Example. I roll a fair die and let X be the resulting number. Find EX, Var(X), and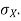

Solution. We have 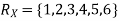  and 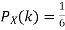for k = 1,2,…,6. Thus we have

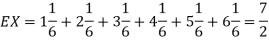
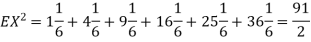
Thus ,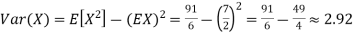

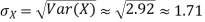
Theorem

For random variable X and real number a and b

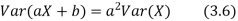
Proof. If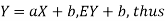

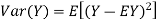
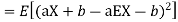
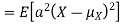
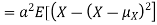
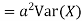
From equation 3.6, we conclude that, for standard deviation, 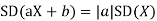. We mentioned that variance is NOT a linear operation. But there is a very important case, in which variance behave like a linear operation and that is when we look at sum of independent random variables,

Theorem

If 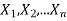are independent random variables and 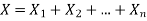, then

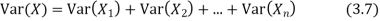
Example. If 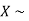Binomial (n, p) find Var (X).

Solution. We know that we can write a Binomial (n, p) random variable as the sum of n independent Bernoulli (p) random variable, i.e.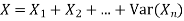

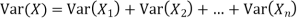
If 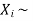Bernoulli (p) then its variance is

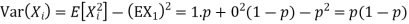
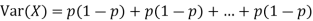
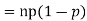
Problem. If 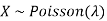, find Var (X).

Solution. We already know 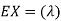, thus Var (X)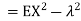. You can find 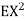directly using LOTUS, however, it is a little easier to find E [X (X-1)] first. In particular using LOTUS we have

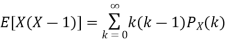
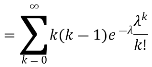
S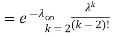

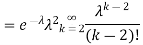
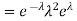
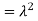
So we have 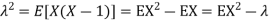. Thus, 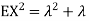and we conclude

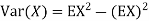
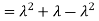
Karl Pearson’s coefficient of correlation-

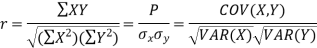
Here- 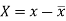and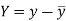

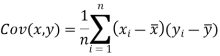
Note-

1. Correlation coefficient always lies between -1 and +1.

2. Correlation coefficient is independent of change of origin and scale.

3. If the two variables are independent then correlation coefficient between them is zero.

Example: Find the correlation coefficient between Age and weight of the following data-

Sol.

x	y					( ) )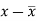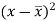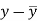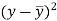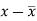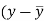
30	56	-10	100	-4	16	40
44	55	4	16	-5	25	-20
45	60	5	25	0	0	0
43	64	3	9	4	16	12
34	62	-6	36	2	4	-12
44	63	4	16	3	9	12
Sum= 240	360	0	202	0	70	32

Karl Pearson’s coefficient of correlation-

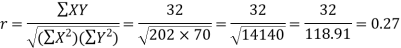
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.

Short-cut method to calculate correlation coefficient-

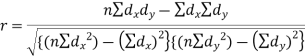
Here,

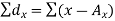
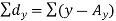
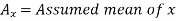
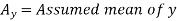
Example: Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-

Sol.

X	Y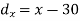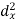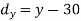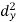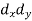
10	90	-20	400	20	400	-400
20	85	-10	100	15	225	-150
30	80	0	0	10	100	0
40	60	10	100	-10	100	-100
50	45	20	400	-25	625	-500
Sum = 150	360	0	1000	10	1450	-1150

Short-cut method to calculate correlation coefficient-

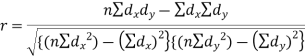
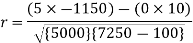
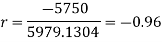
Spearman’s Rank Correlation

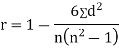
Solution: Let 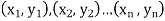be the ranks of 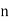individuals corresponding to two characteristics.

Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3, 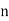and hence their arithmetic means are, each

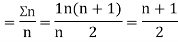
Let 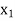, , 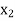, 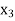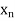be the values of variable 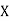and 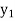, , 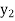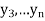those of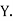

Then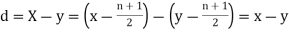

Where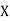 and y are deviations from the mean.

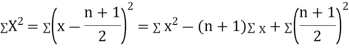
Clearly, and

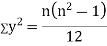
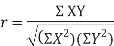
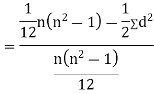
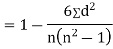
SPEARMAN’S RANK CORRELATION COEFFICIENT:

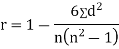
Where 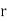denotes rank coefficient of correlation and 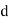refers to the difference ofranks between paired items in two series.

Example: Compute Spearman’s rank correlation coefficient r for the following data:

Solution:

Person	Rank Statistics	Rank in income	d=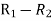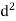
A	9	1	8	64
B	10	2	8	64
C	6	3	3	9
D	5	4	1	1
E	7	5	2	4
F	2	6	-4	16
G	4	7	-3	9
H	8	8	0	0
I	1	9	-8	64
J	3	10	-7	49

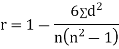
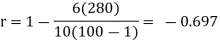
Example: If X and Y are uncorrelated random variables, the 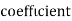of correlation between 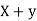and

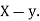
Solution:

Let 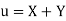and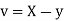

Then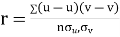

Now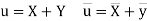

Similarly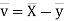

Now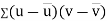

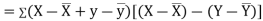
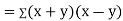
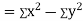
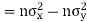
Also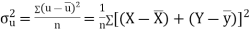

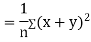
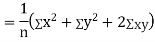
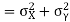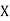(As and 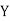are not correlated, we have )

Similarly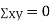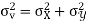

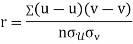
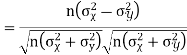
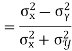
1.7. Chebyshev's Inequality

Markov and Chebyshev Inequalities

Let X be any positive continuous random variable, we can write

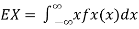
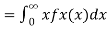
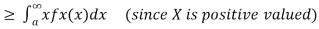
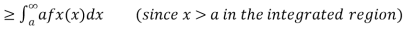
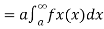
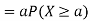
Thus, we conclude

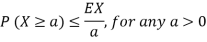
We can prove the above inequality for discrete or mixed random variables similarly (using the generalized PDF), so we have the following result called Markov's inequality.

Markov Inequality

If X is any non negative random variable then

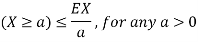
Example 1. Prove the union bound using Markov's inequality.

Solution. Similar to the discussion in the previous section, let 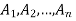be any events and X be the number events 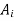that occur. We saw that

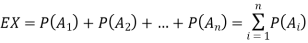
Since X is a non negative random variable we can apply Markov's inequality. Choosing a = 1, we have

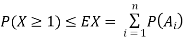
But note that )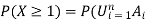

Example 2. Let X ~ binomial (n, p). Using Markov's inequality, find an upper bound on P(X ≥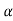n), where 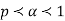. Evaluate the ground for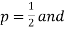

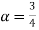
Solution. Note that X is a non negative random variable and EX = np. Applying Markov's inequality we obtain

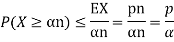
For 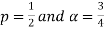,we obtain

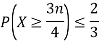
Chebyshev's Inequality

Let X be any random variable. If you define 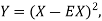then Y is a nonnegative random variable so we can apply Markov''s inequality to Y. In particular for any positive real number b, we have

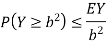
But note that

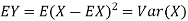
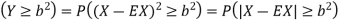
Thus we conclude that

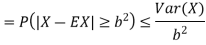
This is Chebyshev’s inequality.

Chebyshev’s inequality

If X is any random variable then for any b>0 we have

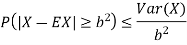
Chebyshev’s inequality states that the difference between X and EX is somehow limited by Var (X). This is intuitively expected as variance shows on average how far we are from the mean.

Example 2. Let X ~ binomial (n, p). Using Markov's inequality, find an upper bound on P(X ≥n), where 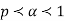. Evaluate the ground for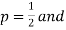

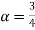
Solution. One way to obtain a bound is to write

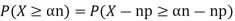
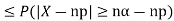
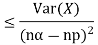
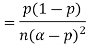
For p = ½ and 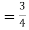, we obtain

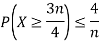
Example. Let X be a random variables such that

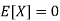
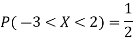
Find a lower bound to its variance.

Solution.

The lower bound can be derived thanks to Chebyshev’s inequality

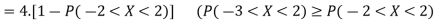
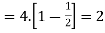
Thus, the lower bound is Var[X]≥2

1.8. The multinomial distribution

Multinomial experiments consists of the following properties-

1. The trials are independent.

2. Each trial has discrete number of possible outcomes.

3. The Experiments consists of n repeated trials.

Note- Binomial distribution is a special case of multinomial distribution.

Multinomial distribution-

A multinomial distribution is the probability distribution of the outcomes from a multinomial experiment.

The multinomial formula defines the probability of any outcome from a multinomial experiment.

Multinomial formula-

Suppose there are n trials in a multinomial experiment and each trial can result in any of k possible outcomes 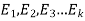. Now suppose each outcome can occur with probabilities .

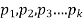Then the probability 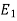occurs 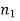times, 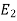occurs 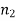times and 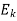occur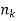s times

Is-

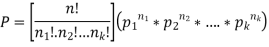
Example: If we have 10 balls in a bag, in which 2 are red, 3 are green and remaining are blue colour balls. Then we select 4 balls randomly form the bag with replacement, then what will be the probability of selecting 2 green balls and 2 blue balls.

Sol.

Here this experiment has 4 trials so n = 4.

The required probability will be-

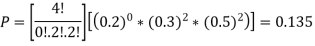
So that-

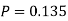
Example: You are randomly drawing cards from an ordinary deck of cards. Every time you pick one you place it back in the deck. You do this 5 times. What is the probability of drawing 1 heart, 1 spade, 1club, and 2 diamonds?

Solution:

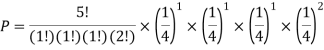
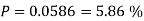
Example: A die weighed or loaded so that the number of spots X that appear on the up face when the die is rolled has pmf

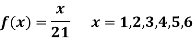
If this loaded die is rolled 21 times. Find the probability of rolling one one, two twos, three threes, four fours, five fives, six sixes.

Solution:

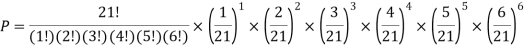
Example: You are given a bag of marble. Inside the bag are 5 red marble, 4 white marble, 3 blue marble. Calculate the probability that with 6 trials you choose 3 marbles that are red, 1 marble that is white and 2 marble is blue. Replacing each marble after it is chosen.

Solution:

1.9. Poisson approximation to the binomial distribution

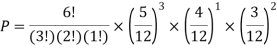
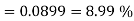
Poisson distribution

If it is a distribution related to the probabilities of events which are extremely rare but which have a large number of independent opportunities for occurrence. The number of persons born blind per year in a large city and the number of deaths by horse cake in an army corps are some of the phenomenon in which this law is followed.

This distribution can be derived as a limiting case of the binomial distribution of making a very large and p very small, keeping up fixed (=m, say).

The probability of r successes in a binomial distribution is

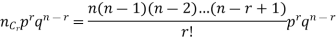
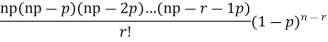
As 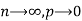(np=m), we have

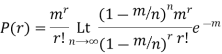
So that the probability of 0,1,2…,r,… successors in a Poisson distribution are given by

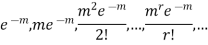
The sum of these probabilities is unity as it should be.

(2) Constants of the Poisson distribution

These constants can easily be derived from the corresponding constants of the binomial distribution simply by making  and noting that np =m

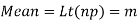
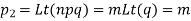
Standard deviation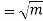

Also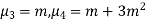

Skewness 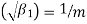, Kurosis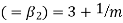

Since 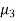is positive, Poisson distribution is positively skewed and since 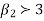, it is Leptokurtic.

(3) Applications of poison distribution.

The distribution is applied to problems concerning:-

(i)                Arrival pattern of defective vehicles in a workshop, patients in a hospital or telephone calls.

(ii)              Demand pattern for certain spare parts.

(iii)           Number of fragments from a shell hitting a target.

(iv)            Spatial distribution of bomb hits.

Example. If the probability of a bad reaction from a certain injection is 0.001, determine the chance that out of 2,000 individuals more than to get a bad reaction.

Solution. It follows a Poisson distribution as the probability of occurrence is very small

Mean m = np = (0.001)=2

Probability that more than two will get bad reaction

= 1- [probability that no one get a bad reaction + probability that one gets a bad reaction + probability that to get bad reaction]

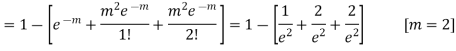
Example. In a certain factory turning out razor blades there is a small chance of 0.002 of any need to be defective. The blades are supplied in packets of 10, use Poisson distribution to calculate the approximate number of packets containing no defective, one defective and to defective blades respectively in a consignment of 10000 packets.

Solution. We know that m = no = 10 × 0.002=0.02

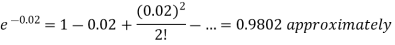
Probability of no defective blade is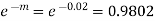

Therefore number of packets containing no defective blade is

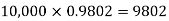
Similarly the number of packets containing one defective blade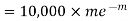

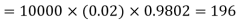
Find the number of packets containing to defective blades

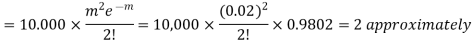
Example. Fit a Poisson distribution to the set of observations:

Solution. Mean =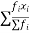

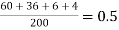
Therefore mean of Poisson distribution i.e. m =0.5

Hence the theoretical frequency for r successes is is

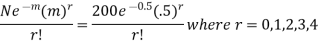
Therefore the theoretical frequencies are

1.10. Infinite sequences of Bernoulli trials.

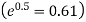
A random experiment whose results are of only two types, for example, success S and failure F, is a Bernoulli test. The probability of success is taken as p, while the probability of failure is q = 1 - p. Consider a random experiment of items in a sale, either sold or not sold. An item produced may be defective or non-defective. An egg is boiled or un-boiled.

A random variable X will have the Bernoulli distribution with probability p if its probability distribution is

P(X = x) = px (1 – p)1−x, for x = 0, 1 and P(X = x) = 0 for other values of x.

Here, 0 is failure and 1 is success.

Conditions for Bernoulli tests

1. A finite number of tests.

2. Each trial must have exactly two results: success or failure.

3. The tests must be independent.

4. The probability of success or failure must be the same in each test.

Problem 1:

If the probability that a light bulb is defective is 0.8, what is the probability that the light bulb is not defective?

Solution:

Probability that the bulb is defective, p = 0.8

Probability that the bulb is not defective, q = 1 - p = 1 - 0.8 = 0.2

Problem 2:

10 coins are tossed simultaneously where the probability of getting heads for each coin is 0.6. Find the probability of obtaining 4 heads.

Solution:

Probability of obtaining the head, p = 0.6

Probability of obtaining the head, q = 1 - p = 1 - 0.6 = 0.4

Probability of obtaining 4 of 10 heads, P (X = 4) = C104 (0.6) 4 (0.4) 6P (X = 4) = C410 (0.6) 4 (0.4) 6 = 0.111476736

Problem 3:

In an exam, 10 multiple-choice questions are asked where only one in four answers is correct. Find the probability of getting 5 out of 10 correct questions on an answer sheet.
 

Solution:

Probability of obtaining a correct answer, p = 1414 = 0.25

Probability of obtaining a correct answer, q = 1 - p = 1 - 0.25 = 0.75

Probability of obtaining 5 correct answers, P (X = 5) = C105 (0.25) 5 (0.75) 5C510 (0.25) 5 (0.75) 5 = 0.05839920044