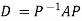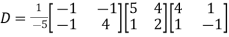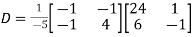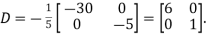Unit – 6
Content
Matrices: It is a rectangular arrangement of numbers formed by keeping them in m numbers of rows and n numbers of columns.
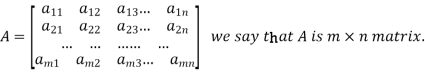
Algebra on Matrices:
- Addition and subtraction of matrices:
Addition and subtraction of matrices is possible if and only if they are of same order.
We add or subtract the corresponding elements of the matrices.
Example: 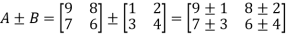
2. Scalar multiplication of matrix:
In this we multiply the scalar or constant with each element of the matrix.
Example: 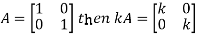
3. Multiplication of matrices: Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
Example: 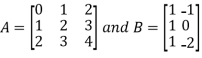
Then 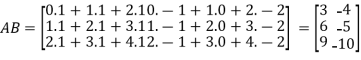
4. Power of Matrices: If A is A square matrix then
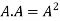
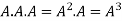 and so on.
and so on.
If 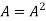 where A is square matrix then it is said to be idempotent.
where A is square matrix then it is said to be idempotent.
5. Transpose of a matrix: The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 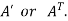
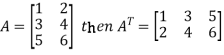
The transpose of matrix  Also
Also 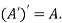
Note: 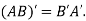
Special Matrix:
Orthogonal Matrices:
A real square matrix A is said to be orthogonal if 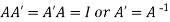
Since 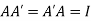 .
.
Taking determinant we get 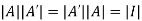
As we know that 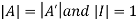
So,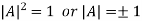 .
.
This implies that determinant of an orthogonal matrix is either 1 or -1.
Note: i) If A is orthogonal, A’ and inverse of A is also orthogonal.
Ii) If A and B are orthogonal then AB is also orthogonal.
Example1: Prove that the following matrix is orthogonal:
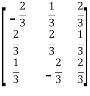
Let A = 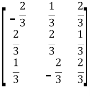 then A’=
then A’= 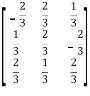
Now, AA’=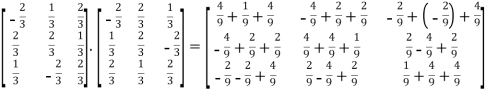
Thus AA’=  = I
= I
Hence the matrix is orthogonal.
Singular Matrix: A square matrix is said to be singular if its determinant is zero otherwise non singular matrix.
i.e. |A|=0 then A is a singular matrix if not non singular.
1.1 Elementary transformation of matrices
It contains three operations one on the rows or columns of the matrix:
- Interchanging- It contain interchange of any two rows or columns .i.e.
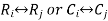
b. Scalar multiplication-It contains scalar multiplication of any scalar quantity with any row or column.
c. Linear combination: we form a linear combination by multiplying a scalar with any row or column and then add the corresponding elements with another row or column.
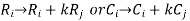 t
t
NOTE: Elementary transformation does not change/affect the order or rank of the matrix.
Elementary matrix: It is obtained from an identity matrix by applying any elementary transformation to it
Row echelon from-
Any matrix is said to be in row echelon form if it follows the term mentioned below:
1. The first non-zero element in each row , is called leading coefficient , is 1. ( some prefers it is not necessary that it should be 1. It can be any number)
2. Each leading entry is in a column to the right of the leading entry in the previous row.
3. Rows with all zero elements are below rows having a non-zero element.
Example of a row echelon form-
 and
and 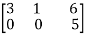
Row reduced form-
A matrix is said to be in reduced row echelon form if it satisfies the following terms-
1. The first non-zero entry in each row is 1.
2. The columns containing this 1 has all the other entries 0.
A matrix in row reduced form is known as row reduced matrix.
For example:
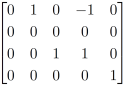

The above matrices are row reduced matrix.
Important definition-
Leading term- the first non-zero entry of any row is called leading term.
Leading column- the column containing the leading term is known as leading column.
Row reduced echelon from-
A matrix is said to be in row reduced echelon form if it has following properties,
1. If the given matrix is already in row reduced form.
2. The row consisting of all zeroes comes below all non zero rows
3. The leading term appear from left to right in successive rows
Some of the examples of row reduced echelon form of the matrices are given below,

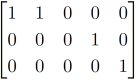
Rank of a matrix-
The rank of a matrix (r) can be defined as –
1. It has atleast one non-zero minor of order r.
2. Every minor of A of order higher than r is zero.
Example: Find the rank of a matrix M by echelon form.
M = 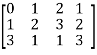
Sol. First we will convert the matrix M into echelon form,
M = 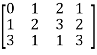
Apply, 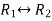 , we get
, we get
M = 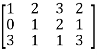
Apply 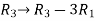 , we get
, we get
M = 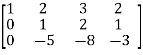
Apply 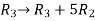
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Example: Find the rank of a matrix A by echelon form.
A = 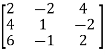
Sol. Convert the matrix A into echelon form,
A = 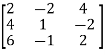
Apply 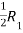
A = 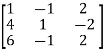
Apply 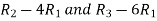 , we get
, we get
A = 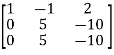
Apply 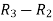 , we get
, we get
A = 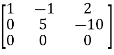
Apply 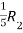 ,
,
A = 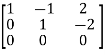
Apply 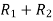 ,
,
A = 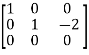
Therefore the rank of the matrix will be 2.
Example: Find the rank of a matrix A by echelon form.
A = 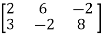
Sol. Transform the matrix A into echelon form, then find the rank,
We have,
A = 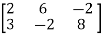
Apply, 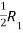
A = 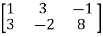
Apply 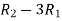 ,
,
A = 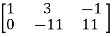
Apply 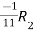
A = 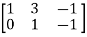
Apply 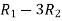
A = 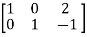
Hence the rank of the matrix will be 2.
This can be done with the help of Gauss-Jordan method. This method used only elementary row transformation, with the help of it we convert the square matrix A to the identity matrix I and the corresponding matrix obtained give the inverse of A.
Gauss –Jordan Method of finding the inverse:
We know that X will be the inverse of a matrix A if
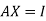
Where I is an identity matrix of order same as A.
We write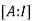 , using elementary operation we covert the matrix A in to a upper triangular matrix. Then compare this matrix with each corresponding column and using back substitution.
, using elementary operation we covert the matrix A in to a upper triangular matrix. Then compare this matrix with each corresponding column and using back substitution.
The determinant of this coefficient matrix is the product of the diagonal elements of the upper triangular matrix.
If this |A|=0 then inverse does not exist.
Example1: Find the inverse of the matrix  by row transformation?
by row transformation?
Let A=
By Gauss-Jordan method
We have 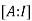
=
Apply 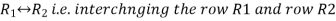

Apply 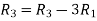 we get
we get
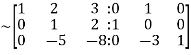
Apply 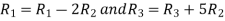 we get
we get
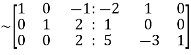
Apply 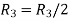
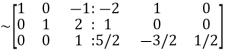
Apply 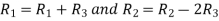
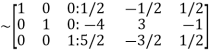
Hence 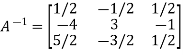
Example2: Find the inverse of 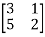
Let A=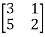
By Gauss-Jordan method
We have 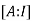
=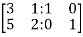
Apply 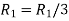
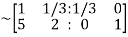
Apply 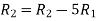
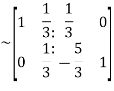
Apply 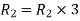
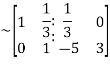
Apply 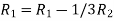
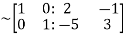
Hence 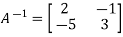
Example3: Find the inverse of the matrix 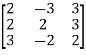 by row transformation?
by row transformation?
Let A= 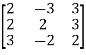
By Gauss-Jordan method
We have 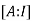
=
Apply 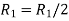 we get
we get
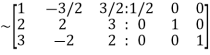
Apply 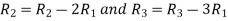
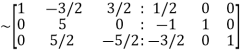
Apply 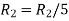
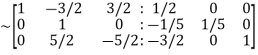
Apply 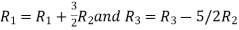
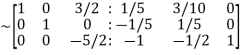
Apply 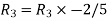
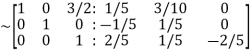
Apply 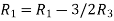
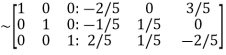
Hence 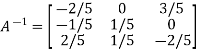
Example4: Find the inverse of 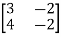
Let A= 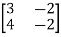
By Gauss Jordan method
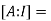
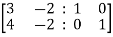
Apply 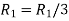
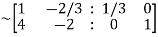
Apply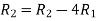
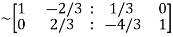
Apply 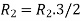
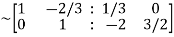
Apply 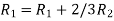
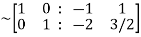
Hence the inverse of matrix A is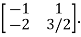
Example5:Find the inverse of 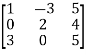
Let A= 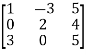
By Gauss-Jordan Method [A:I]
= 
Apply 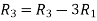
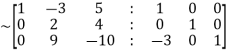
Apply 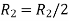

Apply 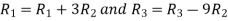
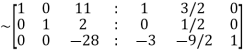
Apply 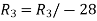
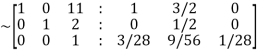
Apply 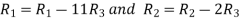
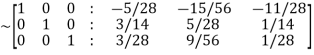
Hence the inverse of matrix A is 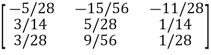
The matrix that we make from the coefficient x,y and z of of the linear equations is reduced into echelon form by elementary row operation.
At the end, we calculate the value of z, and value of y and x are calculated by backward substitution.
Example: find the solution of the following linear equations.
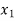 +
+ 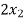 -
- 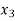 = 1
= 1
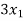 -
- 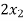 +
+ 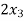 = 2
= 2
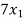 - 2
- 2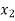 +
+ 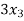 = 5
= 5
Sol. These equations can be converted into the form of matrix as below-
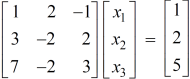
Apply the operation, 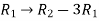 and
and 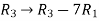 , we get
, we get
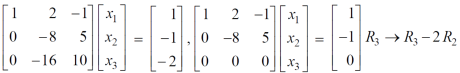
We get the following set of equations from the above matrix,
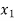 +
+ 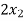 -
- 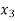 = 1 …………………..(1)
= 1 …………………..(1)
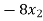 + 5
+ 5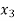 = -1 …………………(2)
= -1 …………………(2)
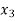 = k
= k
Put x = k in eq. (1)
We get,
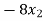 + 5k = -1
+ 5k = -1
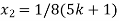
Put these values in eq. (1), we get
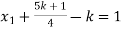
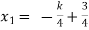
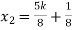 and
and 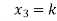
These equations have infinitely many solutions.
Guass- Jordan method –
This method is the modification of gauss elimination method
Example: solve the following system of equations by gauss-jordan method
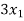 +
+ 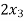 - 2
- 2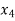 = 0
= 0
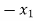 +
+ 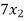 +
+ 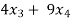 = 0
= 0
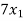 - 7
- 7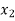 +
+ 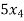 = 0
= 0
Sol. The given system of equations can be written in the form of matrices as follows,
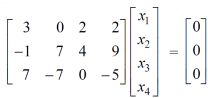
By applying operation - 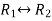 we get,
we get,
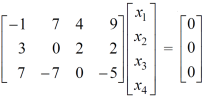
Now apply, 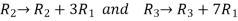
We get,
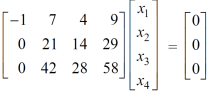
Apply, 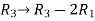
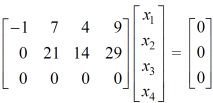
The set of the equations we get from above matrices,
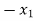 +
+ 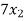 +
+ 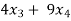 = 0 …………………..(1)
= 0 …………………..(1)
21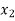 +
+ 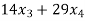 = 0 …………………………..(2)
= 0 …………………………..(2)
Suppose 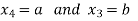
From equation-2, we get
21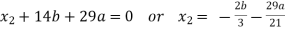
Now from equation-1:
-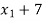 (
(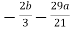 ) + 4b + 9a = 0
) + 4b + 9a = 0
We get,
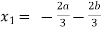
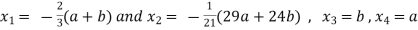
Example: solve the following system of equations by gauss-jordan method
2x + y + 2z = 10
X + 2y + z = 8
3x + y – z = 2
Sol. We will write the equations in matrix form as follows,
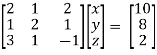
Now apply operation, 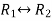

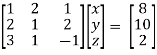
Apply 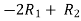 , we get,
, we get,

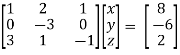
Apply, 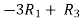 , we get,
, we get,

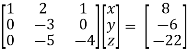
Apply, 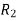 / -3 , we get
/ -3 , we get

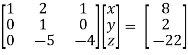
Apply 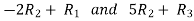

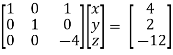
Apply 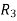 / -4, we get
/ -4, we get

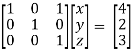
Finally apply 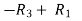
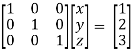
Therefore the solution of the set of linear equations will be,
x = 1 , y = 2 , z = 3
Example: solve the following system of equations by gauss-jordan method.
6a + 8b +6c + 3d = -3
6a – 8b + 6c – 3d = 3
8b - 6d = 6
Sol. Change the system of linear equations into matrix form,
The augmented matrix format will be,
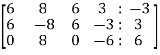
Apply 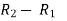
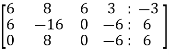
Apply 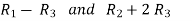
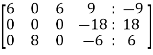
Apply 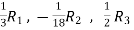
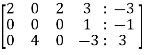
Apply 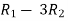 and
and 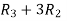

Apply 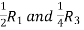

Apply 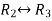

This is the reduced row echelon form,
The system of linear equations becomes,
a + c = 0
b = 0
d = -1
Suppose c = t be a free variable,
Then the solution will be,
a = -t
b = 0
c = t
d = -1
For any number ‘t’.
Let A is a square matrix of order n. The equation formed by
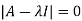
Where I is an identity matrix of order n and 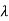 is unknown. It is called characteristic equation of the matrix A.
is unknown. It is called characteristic equation of the matrix A.
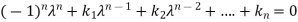
The values of the 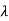 are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
Corresponding to each Eigen value there exist vectors X,
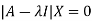
Called the characteristics vectors or latent vectors or Eigen vectors of the matrix A.
Note: Corresponding to distinct Eigen value we get distinct Eigen vectors but in case of repeated Eigen values we can have or not linearly independent Eigen vectors.
If 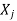 is Eigen vectors corresponding to Eigen value
is Eigen vectors corresponding to Eigen value 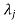 then
then 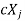 is also Eigen vectors for scalar c.
is also Eigen vectors for scalar c.
Properties of Eigen Values:
- The sum of the principal diagonal element of the matrix is equal to the sum of the all Eigen values of the matrix.
Let A be a matrix of order 3 then 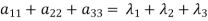
2. The determinant of the matrix A is equal to the product of the all Eigen values of the matrix then 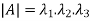 .
.
3. If 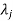 is the Eigen value of the matrix A then 1/
is the Eigen value of the matrix A then 1/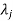 is the Eigen value of the
is the Eigen value of the 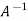 .
.
4. If 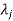 is the Eigen value of an orthogonal matrix, then 1/
is the Eigen value of an orthogonal matrix, then 1/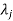 is also its Eigen value.
is also its Eigen value.
5. If 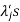 are the Eigen values of the matrix A then
are the Eigen values of the matrix A then 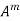 has the Eigen values
has the Eigen values 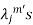 .
.
Example1: Find the sum and the product of the Eigen values of 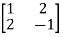 ?
?
The sum of Eigen values = the sum of the diagonal elements
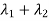 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
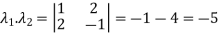
On solving above equations we get 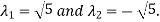
Example2: Find out the Eigen values and Eigen vectors of  ?
?
The Characteristics equation is given by 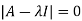
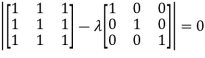
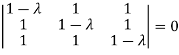
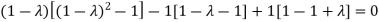
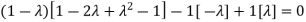
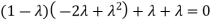
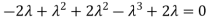
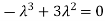
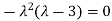
Or 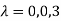
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 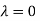 is
is
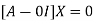
Where X is the column matrix of order 3 i.e.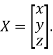
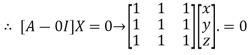
This implies that 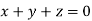
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1)=2 linearly independent solutions.
Let 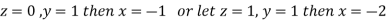
Thus the Eigen vectors corresponding to the Eigen value 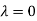 are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 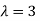 is
is
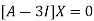
Where X is the column matrix of order 3 i.e.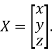
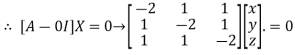
This implies that 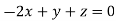
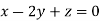
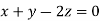
Taking last two equations we get
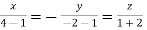
Or 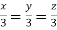
Thus the Eigen vectors corresponding to the Eigen value 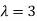 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Example3: Find out the Eigen values and Eigen vectors of 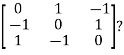
Let A =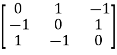
The characteristics equation of A is 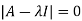 .
.
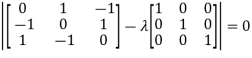
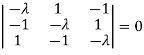
Or 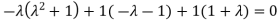
Or 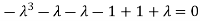
Or 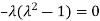
Or 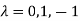
The Eigen vector corresponding to Eigen value 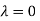 is
is
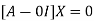
Where X is the column matrix of order 3 i.e.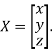
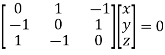
Or 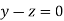
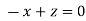
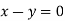
On solving we get 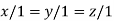
Thus the Eigen vectors corresponding to the Eigen value 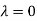 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 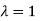 is
is
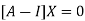
Where X is the column matrix of order 3 i.e.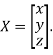
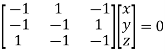
Or 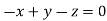
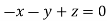
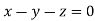
On solving 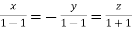 or
or 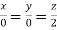 .
.
Thus the Eigen vectors corresponding to the Eigen value 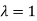 is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 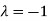 is
is
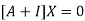
Where X is the column matrix of order 3 i.e.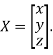
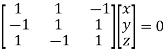
Or 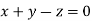
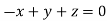
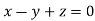
On solving we get 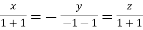 or
or 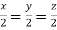 .
.
Thus the Eigen vectors corresponding to the Eigen value 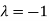 is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
It states that every square matrix A when substituted in its characteristics equation, will satisfies it.
Let A is a square matrix of order n. The characteristic equation of the matrix A.
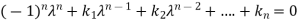
Then according to Cayley-Hamilton theorem
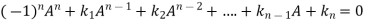
We can also find the inverse of A ,
Multiplying 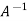 on both side of above equation we get
on both side of above equation we get
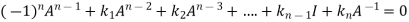
Or 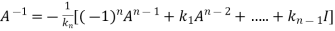
Example1: Verify the Cayley-Hamilton theorem and find the inverse.
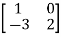 ?
?
Let A =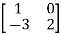
The characteristics equation of A is 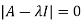
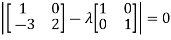
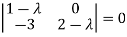
Or 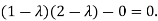
Or 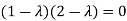
Or 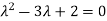
By Cayley-Hamilton theorem 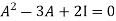
L.H.S: 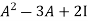
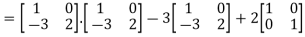
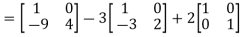
= 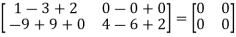 =0=R.H.S
=0=R.H.S
Multiply both side by 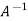 on
on 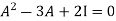
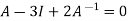
Or 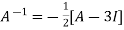
Or 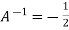 [
[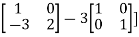
Or 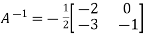
Example2: Verify the Cayley-Hamilton theorem and find the inverse.
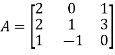
The characteristics equation of A is 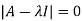
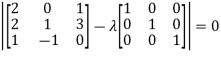
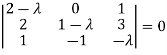
Or 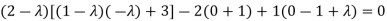
Or 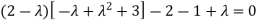
Or 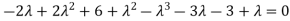
Or 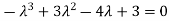
Or 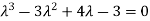
By Cayley-Hamilton theorem 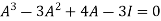
L.H.S. 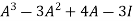
=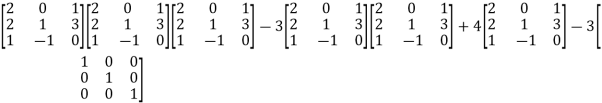
=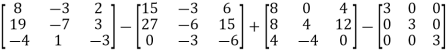
=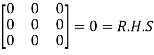
Multiply both side with 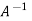 in
in 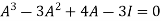
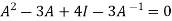
Or 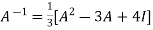
Or 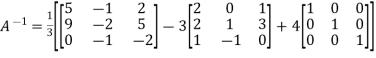
=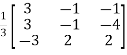
Example3: Using Cayley-Hamilton theorem, find 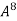 , if A =
, if A = 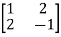 ?
?
Let A =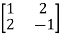
The characteristics equation of A is 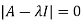
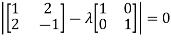
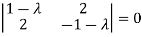
Or 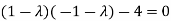
Or 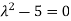
By Cayley-Hamilton theorem 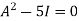
L.H.S. 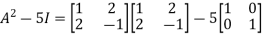
=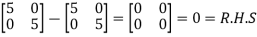
By Cayley-Hamilton theorem we have 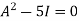
Multiply both side by 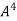
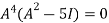 .
.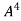
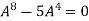
Or 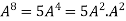
=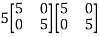
=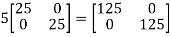
Two square matrix 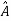 and A of same order n are said to be similar if and only if
and A of same order n are said to be similar if and only if
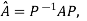 for some non singular matrix P.
for some non singular matrix P.
Such transformation of the matrix A into 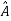 with the help of non singular matrix P is known as similarity transformation.
with the help of non singular matrix P is known as similarity transformation.
Similar matrices have the same Eigen values.
If X is an Eigen vector of matrix A then  is Eigen vector of the matrix
is Eigen vector of the matrix 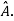
Reduction to Diagonal Form:
Let A be a square matrix of order n has n linearly independent Eigen vectors which form the matrix P such that
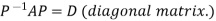
Where P is called the modal matrix and D is known as spectral matrix.
Procedure: let A be a square matrix of order 3.
Let three Eigen vectors of A are 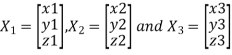 corresponding to Eigen values
corresponding to Eigen values 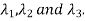
Let 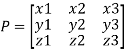
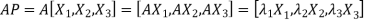 {by characteristics equation of A}
{by characteristics equation of A}
Or 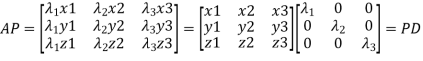
Or 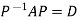
Note: The method of diagonalization is helpful in calculating power of a matrix.
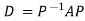 .Then for an integer n we have
.Then for an integer n we have 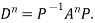
We are using the example of 1.6*
Example1: Diagonalise the matrix 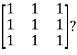
Let A= 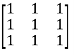
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values 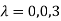 .
.
Then 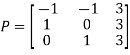 and
and 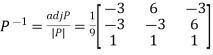
Also we know that 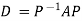
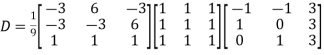
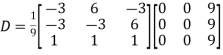
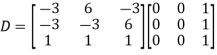
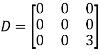
Example2: Diagonalise the matrix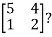
Let A =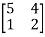
The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values 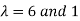 .
.
Then 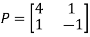 and also
and also 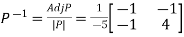
Also we know that