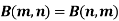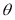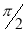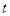Unit -1
Content
Consider

Then limit of f(x) and g(x) both are zero when 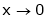 then
then
L becomes  form.
form.
This form is called indeterminate form. The other indeterminate formal are 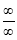 ,
,  ,
, 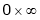 ,
,  , OO,
, OO, 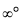 etc.
etc.
To evaluate limit in this case we use L – Hospital rule
L – Hospital rule for 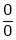 and
and 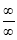
Statement:
If 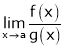 takes either
takes either 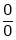 or
or 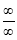
Indeterminate form, then
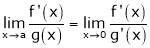 Provided limit is exist
Provided limit is exist
If 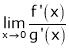 again takes either
again takes either 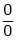 or
or  .
.
Then  ; limit is exist
; limit is exist
We continue the procedure until the limit is exist.
Exercise 1
Evaluate 
Solution:
Let
 …
… 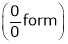
 By L – Hospital rule,
By L – Hospital rule,
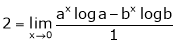
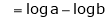

Exercise 2
Evaluate 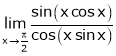
Solution:
Let
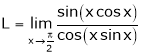 …
… 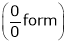
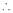 By L – Hospital rule
By L – Hospital rule
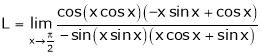

Exercise 3
Evaluate 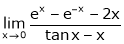
Solution:
Let
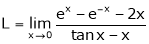 …
… 
 By L – Hospital rule
By L – Hospital rule
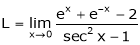 …
… 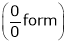
 …
… 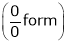
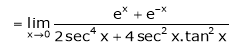

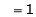
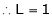
Find the value of a, b if 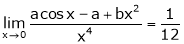
Solution:
Let
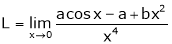 …
… 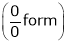
 By L – Hospital rule
By L – Hospital rule
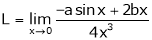 …
… 
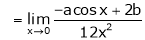 …
… 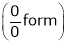
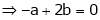 … (1)
… (1)
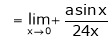 …
… 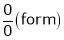

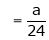
But 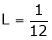

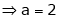
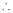 From equation (1)
From equation (1)
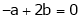
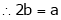
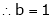
Evaluate 
Solution:
Let
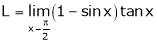 …
… 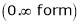
 …
… 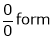
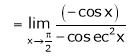 (By L – Hospital Rule)
(By L – Hospital Rule)
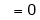
Evaluate 
Solution:
Let
 … 0o form
… 0o form
Taking log on both sides we get,
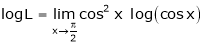 …
… 
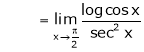 …
… 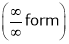
 By L – Hospital Rule
By L – Hospital Rule
i.e. 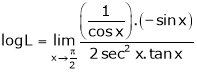



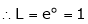

Evaluate 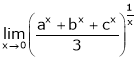
Solution:
Let
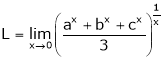 …
… 
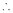 Taking log on both sides,
Taking log on both sides,
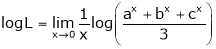
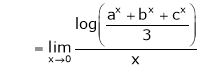 …
… 
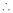 By L – Hospital rule,
By L – Hospital rule,
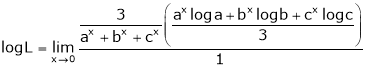
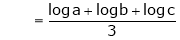
i.e. 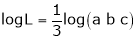
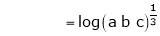
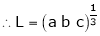
Evaluate 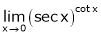
Solution:
Let
 …
… 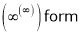
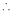 Taking log on both sides, we get
Taking log on both sides, we get

 …
… 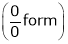
 By L – Hospital Rule,
By L – Hospital Rule,
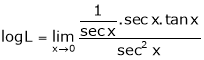
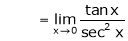

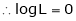

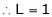
(1) Let f is function defined on [a , ∞) and it is integrable on [a , t] for all t >a, then
If 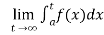 exists , then we define the improper integral of f over [a , ∞) as follows-
exists , then we define the improper integral of f over [a , ∞) as follows-
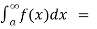
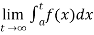
(2) Let f is function defined on (-∞,b] and it is integrable on [t , b] for all t >b, then
If 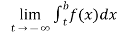 exists , then we define the improper integral of f over (-∞ , b] as follows-
exists , then we define the improper integral of f over (-∞ , b] as follows-
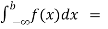
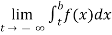
(3) ) Let f is function defined on (-∞, ∞] and it is integrable on [a , b] for every closed and bounded interval [a , b] which is the subset of R., then
If 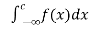 and
and 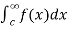 exist for some c belongs to R , then we define the improper integral of f over (-∞ , ∞ ) as follows-
exist for some c belongs to R , then we define the improper integral of f over (-∞ , ∞ ) as follows-
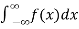 =
= 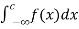 +
+ 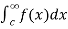
(4) Let f is function defined on (a , ∞) and  exists for all t>a , then
exists for all t>a , then
If 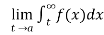 exists , then we define the improper integral of f over (a , ∞) as follows-
exists , then we define the improper integral of f over (a , ∞) as follows-
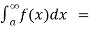
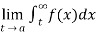
(5) ) Let f is function defined on (-∞ , b) and 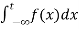 exists for all t<b , then
exists for all t<b , then
If 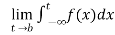 exists , then we define the improper integral of f over (-∞ , b) as follows-
exists , then we define the improper integral of f over (-∞ , b) as follows-
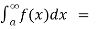
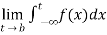
Improper integrals over finite intervals-
(1) Let f is function defined on (a, b] and 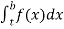 exists for all t ∈(a,b) , then
exists for all t ∈(a,b) , then
If 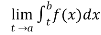 exists , then we define the improper integral of f over (a , b] as follows-
exists , then we define the improper integral of f over (a , b] as follows-
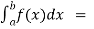
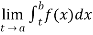
(2) Let f is function defined on [a, b) and 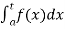 exists for all t ∈(a,b) , then
exists for all t ∈(a,b) , then
If 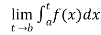 exists , then we define the improper integral of f over [a , b) as follows-
exists , then we define the improper integral of f over [a , b) as follows-
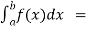
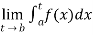
(3) Let f is function defined on [a, c) and (c , b] . If 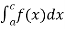 and
and 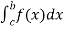 exist
exist
Then we define the improper integral of f over [a , b] as follows-
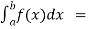
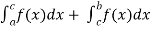
We will read more about the uses of improper integrals in the next topic.
As we have read about improper integrals , we will understand how to check the convergence and divergence of the integrals.
Rules for convergence/ divergence
(1) if the limit exists and a finite number then the integral is said to be convergent.
(2) if the limit does not exists then the integral is said to be divergent.
Example-1: find out the integral 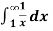 is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
Sol. Here we will convert the integral into limit ,
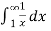 =
= 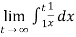
= 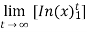
= 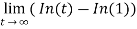
= ∞
As we can see , here limit does not exist. i.e. that is infinity.
So we can say that the given integral is divergent.
Example-2: find out the integral 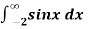 is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
Sol. Covert to the limit ,
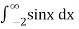 =
= 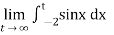
= 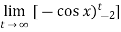
= 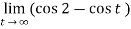
Again the limit does not exist that means the integral is divergent.
Example-3: find out the integral 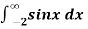 is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
Sol. Follow the same process as we did above,
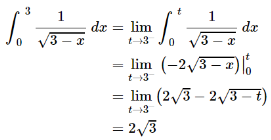
Here limit exists and finite , so that the integral is convergent. And its value is 2√3.
Example-4: find out the integral 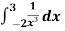 is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
Sol. As we see, the given is integrand is not continuous at x = 0 , we will split the integral,
 =
= 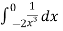 +
+ 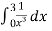
We will check one by one whether the integrals are convergent or divergent,

As we found that, integral is divergent
We don’t need to check for the second one.
A function,
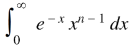
Is called gamma function of n , which can be written as,
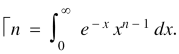
Some important results-
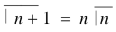
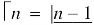
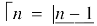
Ex.1: Evaluate 0∞ x3/2 e -x dx
Solution: 0∞ x3/2 e -x dx = 0∞ x 5/2-1 e -x dx
= γ(5/2)
= γ(3/2+ 1)
= 3/2 γ(3/2 )
= 3/2 . ½ γ(½ )
= 3/2 . ½ .π
= ¾ π
Ex. 2: Find γ(-½)
Solution: (-½) + 1 = ½
γ(-1/2) = γ(-½ + 1) / (-½)
= - 2 γ(1/2 )
= - 2 π
Ex. 3. Show that 

Solution :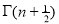 =
= 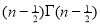
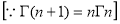
= 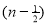
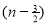
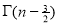
= 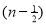
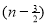
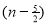
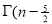 ) .......................
) .......................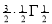
= 
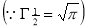
= 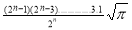


Ex. 4: Evaluate 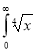
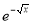 dx.
dx.
Solution : Let 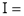
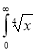
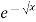 dx
dx
X | 0 |  |
t | 0 | 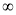 |
Put 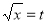 or
or 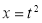 ;dx =2t dt .
;dx =2t dt .
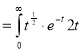 dt
dt
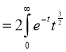 dt
dt
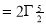

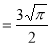
Ex. 5: Evaluate 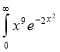 dx.
dx.
Solution : Let 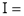
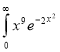 dx.
dx.
x | 0 | 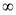 |
t | 0 | 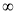 |
Put 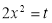 or
or 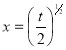 ; 4x dx = dt
; 4x dx = dt
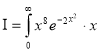 dx
dx
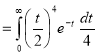

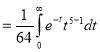
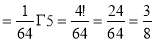
Definition : Beta function
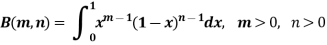
|
Properties of Beta function : |
2. 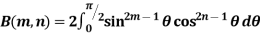 |
3.  |
4. 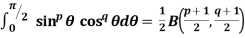 |
Example(1): Evaluate I = 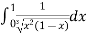
Solution:
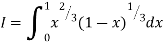
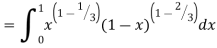
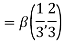
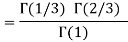
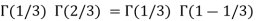
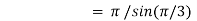
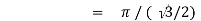
= 2 π/3
Example(2): Evaluate: I = 02 x2 / (2 – x ) . Dx
Solution:
Letting x = 2y, we get
I = (8/2) 01 y 2 (1 – y ) -1/2dy
= (8/2) . B(3 , 1/2 )
= 642 /15
BETA FUNCTION MORE PROBLEMS
Relation between Beta and Gamma functions :
 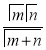 | ||||||
Example(1): Evaluate: I = 0a x4 (a2 – x2 ) . Dx Solution: Letting x2 = a2 y , we get I = (a6 / 2) 01 y 3/2 (1 – y )1/2dy = (a6 / 2) . B(5/2 , 3/2 ) = a6 /3 2 Example(2): Evaluate: I = 02 x (8 – x3 ) . Dx Solution: Let x3 = 8y I = (8/3) 01 y-1/3 (1 – y ) 1/3 . Dy
= (8/3) B(2/3 , 4/3 ) = 16 π / ( 9 3 ) Example(3): Prove that 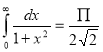 Solution : Let   Put 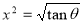 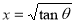 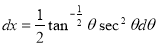 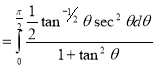 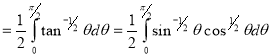 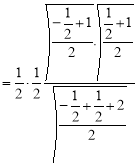 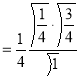 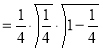 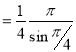 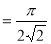  Example(4): Evaluate 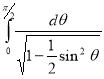 Solution :Let 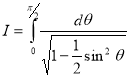 Put 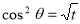 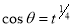  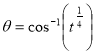 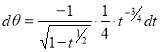 When 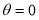 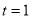 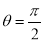 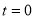
Also 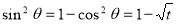 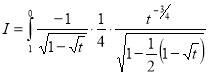 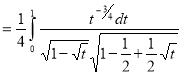 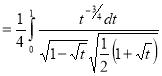 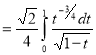 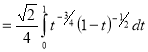 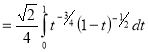 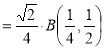  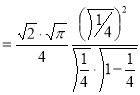 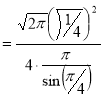 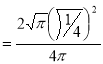 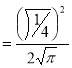
Example(5): Show that 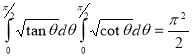 Solution : 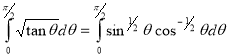 = 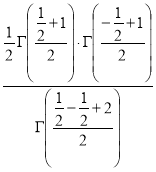 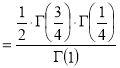 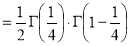 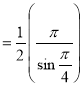  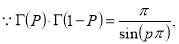 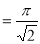  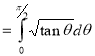 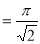   Exercise : - Q. Show that 1. 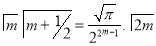 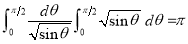 |
There is wide range of definite integrals such as, from geometric applications to physical world problems.
We will study about these applications one by one-
(1) Area between the curves-
Suppose we want to find out the area between y = f(x) and y = g(x) on interval [a,b] such that f(x) ≥ g(x). See the figure
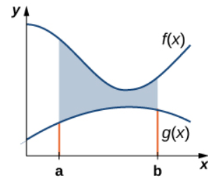
Let the area between the two curve is A, then
A = 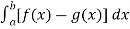
Lets do some examples,
Example-1: find the area under the curves where f(x) = x+4 and g(x) = 3 – x/2 over the interval [1,4]
Sol. Here limits are given a = 1 , b = 4,
We know that, area under the curve,
A = 
= 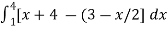
= 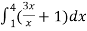
= 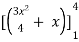
= (16 – 7/4) = 57/4
So that the area of the region is 57/4 unit square.
Example-2: find the area under the curves where y = x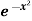 and y = x + 1, x = 2 and y-axis.
and y = x + 1, x = 2 and y-axis.
Sol. When we draw the graph, curve does not meet, but depend on two vertical lines,
Here boundary is [0 , 2]
Area under the curve,
A = 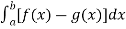
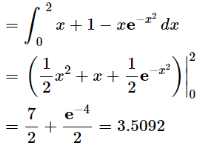
So that the area under the curve is 3.2092 unit square.
Example-2: Determine the area under the curves y = 2x² + 10 and y = 4x + 16.
Sol. Here we will find out the intersection, which are the boundaries of the curve,
2x² + 10 = 4x + 16
2x² - 4x – 6 = 0
2 (x + 1) ( x – 3 ) = 0
We get, x = -1 and x = 3,
We know that, Area under the curve,
A = 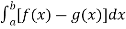
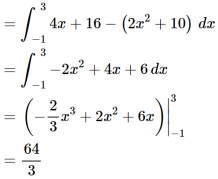
(2) Average function value-
We can use definite integrals to find out the average value of a function.
The average value of a function over the interval [a , b] is given by the following expression ,
f( avg.) = 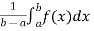
Example-1: find the average value of the function f(x) = x³ over the interval[0,1].
Sol. We know that
f( avg.) = 
= 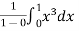 =
= 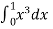 = 1 / 4
= 1 / 4
Example-2: find the average value of f(x) = cos x over the interval [0 , 𝛑/2]
Sol. We know that,
f( avg.) = 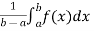
Put the values , we get
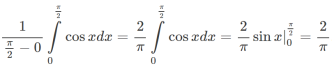
(3) Work-
This one is the easiest use of definite integral
We know that work done, when a constant force F is applied to move the object over a distance d.
W = Fd
Now suppose that the force at any point x is F(x) , the the work done by to move the object from x = a to x = b is,
W = 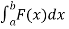
Example-1: Find the work done on a spring when we compress it from its natural length of 1m to the 0.75m , if the spring constant k = 16 N / m.
Sol. The force is given by,
F =16x
Here we start to compress it at x = 0 and finish at x= 0.25 from its natural length.
So we take lower limit and upper limit 0 and 0.25 respectively.
We know that,
W = 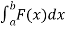
= 
= 0.5 N.m
Example-2: A force of 1200 N compresses a spring from its natural length of 18 cm to a length of 16 cm. How much work is done in compressing it from 16 cm to 14 cm?
Sol. Here,
F = kx
So that,
1200 = 2k
K = 600 N/cm
In that case,
F = 600x
We know that,
W = 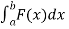
W = 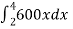 , which gives
, which gives
W = 3600 N.cm
Suppose A(x) represents the area of the cross section at any point x over the interval [a,b], then the volume of the solid is represented by,
V(S) = 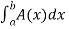
This method is known as slicing method.
Example-1: find out the volume of pyramid with square base by slicing method.
Sol.
Here pyramid has square base , then its volume will be V =  a²h , where a is the length of side of base.
a²h , where a is the length of side of base.
We will derive this formula by slicing method.
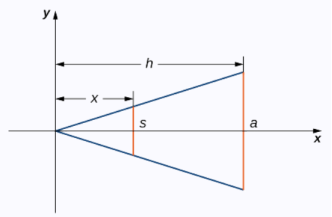
In the above figure , there is a pyramid on x-axis,
Here we see that there are similar tirangles,
Then by basic proportionality theorem( BPT) that we have studied in high school,
We get,
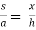
Which gives,
s = 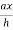
Then the area of cross sectional squares,
A(x) = s² = 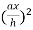
To find the volume of pyramid , we integrate from 0 to h,
V= 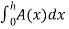 =
=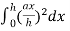 =
= 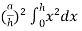 ,
,
Which gives,
V =  a²h.
a²h.
This is formula for volume of pyramid with square base.
Example-2: using slicing method, find out the volume of solid of revolution bounded by f(x) = x² - 4x +5 , x = 1 and x = 4, rotated about the x-axis.
Sol. Intervals are given. [ 1 , 4]
Here the solid is formed by revolving the region about x-axis , the cross – sections are circle .
Area of the cross section is , then is the area of circle, here radius of the circle is given by f(x).
We know that,
Area of the circle= π r²
= π [f(x)]²
= π[x² - 4x +5]²
Volume will be,
V = 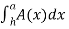
= 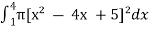
= 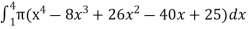 which gives,
which gives,
= 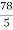 π
π
So the volume is 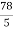 π
π
Example-3: Find the volume of the solid of revolution generated by rotating the region between the graph of f(x) = √x over the interval [1,4] around x-axis.
Sol. The graph of the function will look like as follow,
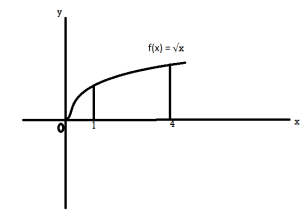
On rotation it will make circle ( cross-section)
We know that,
V = 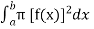
= 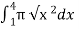 =
= 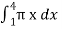 , which gives
, which gives
= 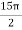
The volume is 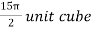
We can use definite integrals to find out the length of the arc of a curve.
Suppose a rocket launched along a parabolic path and if we are interested to find the length of the how much distance has rocket covered the we can use the concept of arc length of curve.
Arc length of the curve y = f(x) –
Let f(x) be a smooth function over the interval [a,b]. Then the arc length of the proportion of f(x) from point (a,f(a)) to the point (b, f(b)) is given by,
Length of Arc = 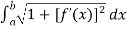
Note - smooth functions- functions which are continuous derivative are called smooth.
Example-1: let f(x) = 2 x³/² , then calculate the arc length of the graph over interval [ 0 , 1].
Sol. Here we can find its first derivative
f’(x) = 3 x¹/²
Such that,
[f’(x)]² = 9x
Then we know that,
Length of Arc = 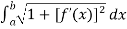
= 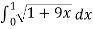
Now,
Let u = 1 + 9x , then du = 9 dx , when x = 0 then u = 1 and x = 1 then u = 10,
So,
= 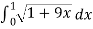
= 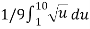
= 1/9 ×2/3 × 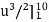 = 2.268 units
= 2.268 units
Example-2: suppose a wire hanging on two poles follows the curve,
f(x) = a cosh(x/a)
Find the length of the wire.
Sol. We will find the first derivative of f(x),
f’(x) = sinh(x/a)
The curve of f(x) will look like,
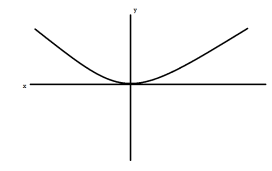
Hence the curve os symmetric, we will measure the length of one side first,
The limits on one side will be, 0 to b
We know that
Length of Arc = 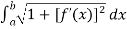
Put f’(x) = sinh(x/a), we get
Length of Arc = 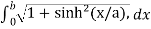
Use the identity,
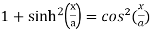
= 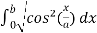
= 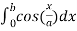
We get on solving,
a sinh(b/a)
On both sides, the length of the curve will be,
2 a sinh(b/a)
Example_3: Find the length of f(x) = x between x = 2 and x = 3.
Sol. The derivative of f(x) will be,
f’(x) = 1
And we know that,
Length of Arc = 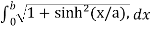
So that,
Length of Arc = 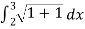
= 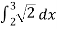
On solving the integral, we get
= (3 – 2) =
= 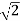 .
.
Suppose we have a curve y = f(x) and if we revolve this curve around x – axis then the area formed is known as surface area of revolution.
Let f(x) be a non-negative smooth function over the interval[ [ a , b] , then the surface area of the surface of revolution formed by revolving the graph of f(x) around x-axis is given by,
S = 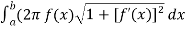
Example-1: find the surface of the surface generated by revolving the graph f(x) = 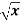 over the interval [1,4] around x-axis.
over the interval [1,4] around x-axis.
Sol. The graph of the function will look like
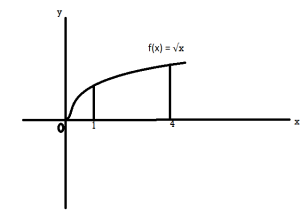
f(x) = 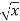 then f’(x) = 1/2 (
then f’(x) = 1/2 (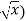
(f’(x))² = 1/4x
Then,
S = 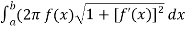
S = 
S = 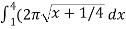 ,
,
Let u = 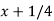 , then du = dx, when x = 1 , u = 5/4 and when x = 4 , u = 17/4,
, then du = dx, when x = 1 , u = 5/4 and when x = 4 , u = 17/4,
This will give,
 =
= 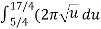
On solving the integral we get,
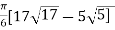 = 30.84 (approx.)
= 30.84 (approx.)
Example-1: find the surface of the surface generated by revolving the graph g(y) = 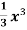 over the interval [0,2] around y-axis.
over the interval [0,2] around y-axis.
Sol. Hint - use formula
S = 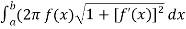
Ans. = 24.118