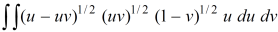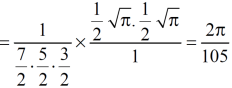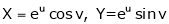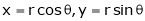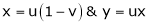Unit -5
Content
Double integral –
Before studying about multiple integrals, first let’s go through the definition of definition of definite integrals for function of single variable.
As we know, the integral
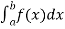
Where is belongs to the limit a ≤ x ≤ b
This integral can be written as follows-
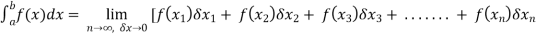
Now suppose we have a function f(x , y) of two variables x and y in two dimensional finite region R in xy-plane.
Then the double integration over region R can be evaluated by two successive integration

Evaluation of double integrals-
If A is described as 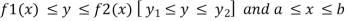
Then,
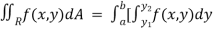 ]dx
]dx
Let do some examples to understand more about double integration-
Example-1: Evaluate 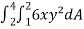 , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
Sol. Let , I = 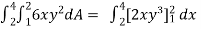
= 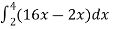
= 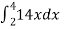
= 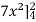
= 84 sq. Unit.
Which is the required area.
Example-2: Evaluate 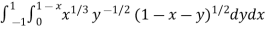
Sol. Let us suppose the integral is I,
I = 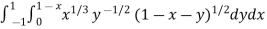
Put c = 1 – x in I, we get
I = 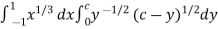
Suppose , y = ct
Then dy = c
Now we get,
I = 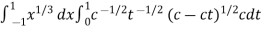
I = 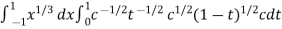
I = 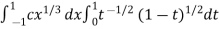
I = 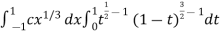
I = 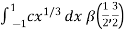
As we know that by beta function,
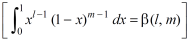
Which gives,
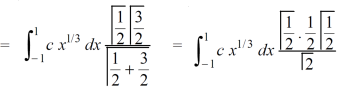
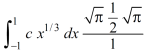

Now put the value of c, we get
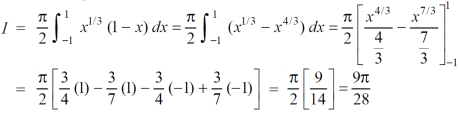
Example-3: Evaluate the following double integral,
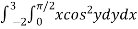
Sol. Let ,
I = 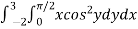
On solving the integral, we get
Consider a function f (x, y) defined in the finite region R of the X-Y plane. Divide R into n elementary areas A1, A2,…,An. Let (xr, yr) be any point within the rth elementary are Ar

Fig. 6.1
f (x, y) dA = f (xr, yr) A
Evaluation of Double Integral when limits of Integration are given (Cartesian Form).
Ex. 1 : Evaluate 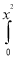 ey/x dy dx.
ey/x dy dx.
Soln. :
Given : I =  ey/x dy dx
ey/x dy dx
Here limits of inner integral are functions of y therefore integrate w.r.t y,
I = 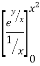
 dx
dx
= 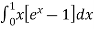
= 
I = 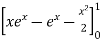
= =
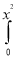 ey/x dy dx =
ey/x dy dx =
Ex. 2 : Evaluate x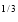 y
y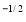 (1 – x –y)
(1 – x –y)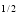 dx dy.
dx dy.
Soln. :
Given : I = x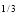 y
y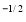 (1 – x –y)
(1 – x –y)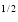 dx dy.
dx dy.
Here the limits of inner integration are functions of y therefore first integrate w.r.t y.
I = x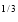 dx
dx 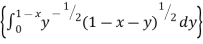
Put 1 – x = a (constant for inner integral)
I = x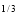 dx
dx 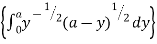
Put y = at dy = a dt
y | 0 | a |
t | 0 | 1 |
I = x dx
dx 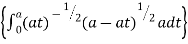
I = x dx
dx 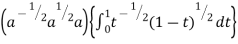
I = x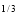 a dx
a dx
I = x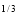 (1 – x) dx = (x
(1 – x) dx = (x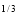 – x4/3) dx
– x4/3) dx
I = 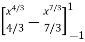
=
I = =
x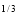 y
y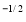 (1 – x –y)
(1 – x –y)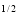 dx dy =
dx dy =
Ex. 3 : Evaluate 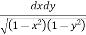
Soln. :
Let, I = 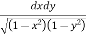
Here limits for both x and y are constants, the integral can be evaluated first w.r.t any of the variables x or y.
I = dy 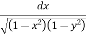
I = 
= 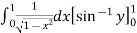
= 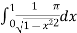
= 
=
= 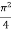
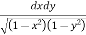 =
=
Ex. 4: Evaluate e–x2 (1 + y2) x dx dy.
Soln. :
Let I = e–x2 (1 + y2) x dy = dy e–x2 (1 + y2) x dy
= dy e– x2 (1 + y2)  dx
dx
= dy [∵ f (x) ef(x) dx = ef(x) ]
= (–1) dy (∵ e– = 0)
= = =
e–x2 (1 + y2) xdx dy =
NOTES:
Type II: Evaluation of Double Integral when region of Integration is provided (Cartesian form)
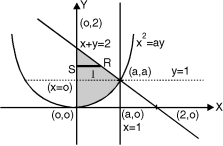
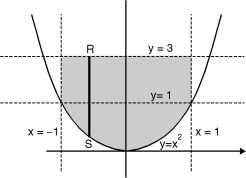
Ex.1: Evaluate y dx dy over the area bounded by x= 0 y =  and x + y = 2 in the first quadrant
and x + y = 2 in the first quadrant
Soln. :
The area bounded by y = x2 (parabola) and x + y = 2 is as shown in Fig.6.2
The point of intersection of y = x2 and x + y = 2.
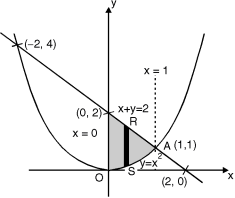
x + x2 = 2 x2 + x – 2 = 0
x = 1, – 2
At x = 1, y = 1 and at x = –2, y = 4
Fig. 6.2
(1, 1) is the point of intersection in Ist quadrant. Take a vertical strip SR, Along SR x constant and y varies from S to R i.e. y = x2 to y = 2 – x.
Now slide strip SR, keeping IIel to y-axis, therefore y constant and x varies from x = 0 to x = 1.
I = 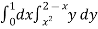
= 
= 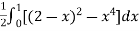
= (4 – 4x + 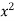 –
– 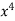 ) dx
) dx
= =
I = 16/15
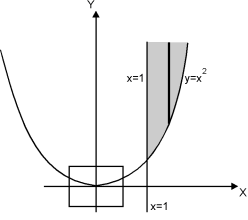
Ex. 2 : Evaluate 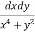 over x 1, y
over x 1, y 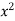
Soln. :
 Let I =
Let I = 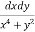 over x 1, y
over x 1, y 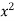
The region bounded by x 1 and y 
Is as shown in Fig. 6.3.
Fig. 6.3
Take a vertical strip along strip x constant and y varies from y = 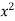
To y = . Now slide strip throughout region keeping parallel to y-axis. Therefore y constant and x varies from x = 1 to x = .
I = 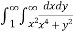
= 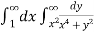
= 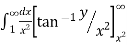 [ ∵
[ ∵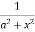 dx = tan–1 (x/a)]
dx = tan–1 (x/a)]
= 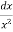 =
=
= – = (0 – 1)
I =
Ex. 3 : Evaluate (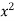 +
+ 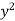 ) dx dy through the area enclosed by the curves y = 4x, x + y = 3 and y =0, y = 2.
) dx dy through the area enclosed by the curves y = 4x, x + y = 3 and y =0, y = 2.
Soln. :
Let I = (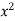 +
+ 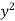 ) dx dy
) dx dy
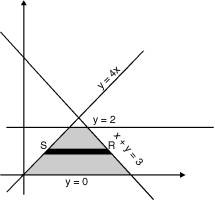 The area enclosed by the curves y = 4x, x + y =3, y = 0 and y = 2 is as shown in Fig. 6.4.
The area enclosed by the curves y = 4x, x + y =3, y = 0 and y = 2 is as shown in Fig. 6.4.
(find the point of intersection of x + y = 3 and y = 4x)
Fig. 6.4
Take a horizontal strip SR, along SR y constant and x varies from x = to x = 3 – y. Now slide strip keeping IIel to x axis therefore x constant and y varies from y = 0 to y = 2.
I = dy (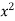 +
+ 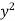 ) dx
) dx
= 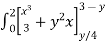
=  +
+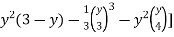 dy
dy
I = 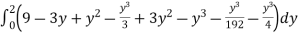
= 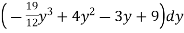
= 
= + – 6 + 18
I =
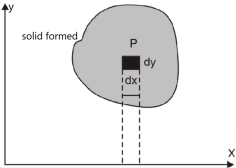
Suppose we have a curve y = f(x) is revolved about an axis , then a solid is generated , now we need to find out the volume of the solid generated ,
Q
The formula for volume of the solid generated about x-axis,

Example-1: Calculate the volume generated by the revolution of a cardioid,
r = a ( 1 – cos θ) about its axis
Sol. Here, r = a ( 1 – cos θ)
Volume = 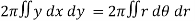
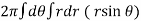
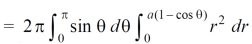
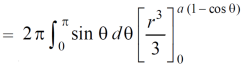
= 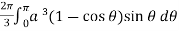
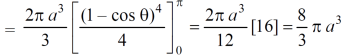
Which is the volume of generated by cardioid.
Example-2: Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
Sol. We know that,
Volume = 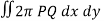
Here , PQ = 3 – x,
= 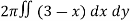
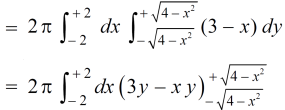
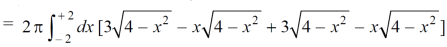
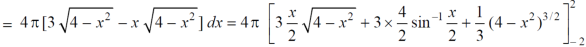
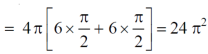
The volume is 24π².
Example-3: Calculate the volume under the surface z = 3 + x² - 2y over the region R defined as 0≤ x ≤ 1 and -x ≤ y ≤ x
Sol. The is a double integral of z = 3 + x² - 2y over the region R .
Volume will be,
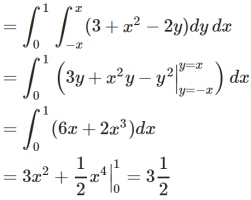
Ex. 1 : Change the order of integration for the integral  and evaluate the same with reversed order of integration.
and evaluate the same with reversed order of integration.
Soln. :
Given, I = 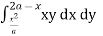 …(1)
…(1)
 In the given integration, limits are
In the given integration, limits are
y = 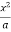 , y = 2a – x and x = 0, x = a
, y = 2a – x and x = 0, x = a
The region bounded by x2 = ay, x + y = 2a Fig.6.5
And x = 0, x = a is as shown in Fig. 6.5
Here we have to change order of Integration. Given the strip is vertical.
Now take horizontal strip SR.
To take total region, Divide region into two parts by taking line y = a.
1 st Region :
Along strip, y constant and x varies from x = 0 to x = 2a – y. Slide strip IIel to x-axis therefore y varies from y = a to y = 2a.
I1 = dy xy dx …(2)
2nd Region :
Along strip, y constant and x varies from x = 0 to x = . Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.
I2 = dy xy dx …(3)
From Equation (1), (2) and (3),
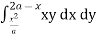 = dy xy dx + dy xy dx
= dy xy dx + dy xy dx
= 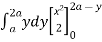 + y dy
+ y dy 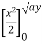
=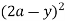 dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2 dy
dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2 dy
= (4a2 y – 4ay2 + y3) dy + y2 dy
= 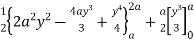
= 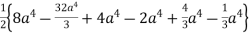 +
+ 
= a4
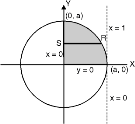
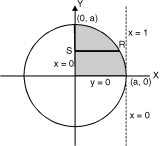 Ex. 2 : Evaluate
Ex. 2 : Evaluate
I = 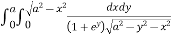
Soln. :
 Given : I =
Given : I = 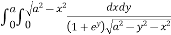 …(1)
…(1)
In the given integration, limits are
x = 0, x = a, y = 0, y = 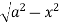
The bounded region is as shown in Fig. **.
In the given, strip is vertical. Now take horizontal strip SR. Along strip y constant and x varies from x = 0 to
x = 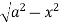 . Slide strip IIel to X-axis therefore y varies from y = 0 to y = a.
. Slide strip IIel to X-axis therefore y varies from y = 0 to y = a.
I = dy 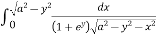
= 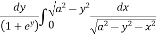
Put a2 – y2 = b2
I = 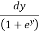
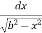
= 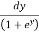 =
= 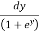
= 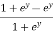 dy =
dy = 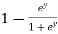 dy
dy
= 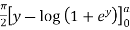
=
= 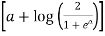
= 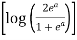 [∵ a = a loge]
[∵ a = a loge]
I = dy 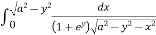 =
= 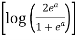
 Ex.3 : Express as single integral and evaluate dy dx + dy dx.
Ex.3 : Express as single integral and evaluate dy dx + dy dx.
Soln. :
Given : I = dy dx + dy dx
I = I1 + I2
The limits of region of integration I1 are
x = – ; x = and y = 0, y = 1 and I2 are x = – 1,
x = 1 and y = 1, y = 3.
The region of integration are as shown in Fig. 6.7
To consider the complete region take a vertical strip SR along the strip y varies from y = x2 to
y = 3 and x varies from x = –1 to x = 1. Fig. 6.7
I = 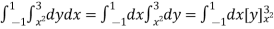
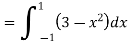
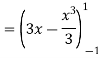
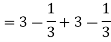
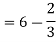

NOTES:
Evaluation of Double Integral by Changing Cartesian to Polar co-ordinates (when limits are given).
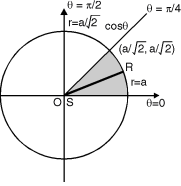
 Ex. 1 : Evaluate
Ex. 1 : Evaluate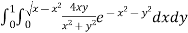
Soln. :
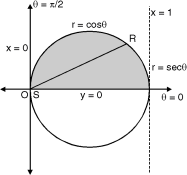
The region of integration bounded by
y = 0, y = 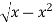 and x = 0, x = 1
and x = 0, x = 1
y = 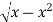 x2 + y2 = x
x2 + y2 = x
The region bounded by these is as shown in Fig. 6.8.
Convert the integration in polar co-ordinates by using x = r cos , y = r sin and dx dy = r dr d
x2 + y2 = x becomes r = cos
y = 0 becomes r sin = 0 = 0
x = 0 becomes r cos = 0 =
And x = 1 becomes r = sec Fig. 6.8
Take a radial strip SR with angular thickness , Along strip constant and r varies from r = 0 to r = cos . Turning strip throughout region therefore varies from = 0 to =
I = 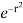 r dr d
r dr d
= 4 cos sin d r 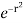 dr
dr
= 4 cos sin d [–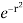 ]
]
= – 2 cos sin [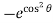 +1] d
+1] d
= – 2 [cos sin 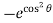 – cos sin ] d
– cos sin ] d
= –2 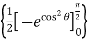 + 2 cos sin d
+ 2 cos sin d
= – + 2
= + 1 =
 Ex. 2: Sketch the area of double integration and evaluate
Ex. 2: Sketch the area of double integration and evaluate
 dxdy
dxdy
Soln. :
Let I = 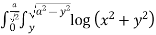 dxdy
dxdy
The region of integration is bounded by the curves
x = y, x = 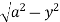 and y = 0, y = Fig. 6.9
and y = 0, y = Fig. 6.9
i.e. x = y, x2 + y2 = a2 and y = 0, y =
The region bounded by these is as shown in Fig. 6.9.
The point of intersection of x = y and x2 + y2 = a2 is x =
Convert given integration in polar co-ordinates by using polar transformation x = r cos , y = r sin and dx dy = r dr d
x = y gives r cos = r sin tan = 1 =
x2 + y2 = a2 r2 = a2 r = a
y = 0 gives r sin = 0 = 0.
y = gives r sin = r = cosec
Take a radial strip SR, along SR constant and r varies from r = 0 to r = a. Turning this strip throughout region therefore varies from = 0 to =
I = log r2 r dr d = 2 d r log r dr
I = 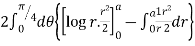
= 2 d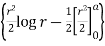
= 2 d
= 2 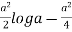 d
d
= 2 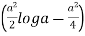 []
[]
I =  [/4] =
[/4] = 
Evaluation of Double Integral when region of Integration is provided (Polar form)
Ex. 1 : Evaluate r4 cos3 dr d over the interior of the circle r = 2a cos
Soln. :
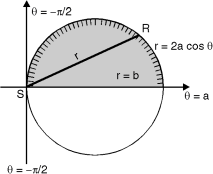 The region of the integration is as shown in Fig. 6.10.Take a radial strip SR, along strip constant and r varies from r = 0 to r = 2a cos. Now turning this strip throughout region therefore varies from = to =
The region of the integration is as shown in Fig. 6.10.Take a radial strip SR, along strip constant and r varies from r = 0 to r = 2a cos. Now turning this strip throughout region therefore varies from = to =
I = r4 cos3 dr d
= cos3 d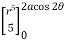
=  cos3 cos5 d
cos3 cos5 d
= 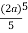 cos8 d Fig. 6.10
cos8 d Fig. 6.10
= 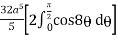
= 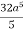 2
2
I = 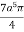
r4 cos3 dr d = 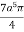
Ex. 2 : Evaluate r sin dr d over the cardioid r = a (1 – cos ) above the initial line.
Soln. :
The cardioid r = a (1 – cos ) is as shown in Fig. 6.11. The region of the integration is above the initial line.
Take a radial strip SR, along strip constant and r Varies from r = 0 to r = a (1 – cos ).
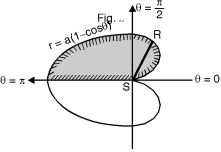 New turning the strip throughout region therefore varies from = 0 to = .
New turning the strip throughout region therefore varies from = 0 to = .
I = r sin dr d
= sin d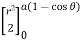
Fig.6.11
= sin [a2 (1 – cos )2]
= 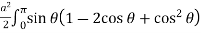
I = 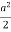 (sin – 2 sin cos + sin
(sin – 2 sin cos + sin 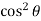 ) d
) d
= 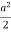 2 (sin – sin2 + sin
2 (sin – sin2 + sin 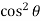 ) d
) d
= 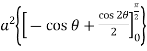 +
+
I = a2= a2
I = 
NOTES:



 Area enclosed by plane curves expressed in Cartesian coordinates:
Area enclosed by plane curves expressed in Cartesian coordinates:


 Y (x,y) P Q (x+dx,y+dy) y=f(x)
Y (x,y) P Q (x+dx,y+dy) y=f(x)


 V U
V U
G H dxdy
 A R S B
A R S B
x=a y=0 x=b X
Consider the area enclosed by the curves 
And 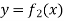 and the ordinates
and the ordinates
Area =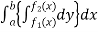
Consider the area enclosed by the curves 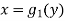
And 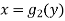 and the ordinates
and the ordinates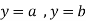
Area =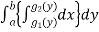
Area enclosed by plane curves expressed in Polar coordinates:
Consider the area enclosed by the polar curves 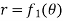
And 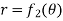 and the line
and the line 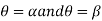
Area =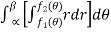
Ex.1: Find the area between the curves 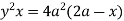 and its asymptote.
and its asymptote.
Solution: The curve is symmetrical about x axis not passing through origin. Also 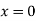 is the asymptote to the curve and intersect x axis at
is the asymptote to the curve and intersect x axis at 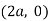 for
for 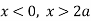 curve doesn’t exists. And for
curve doesn’t exists. And for 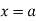 and
and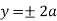 . Because of symmetry
. Because of symmetry
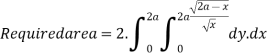
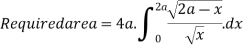
Put 
x | 0 | 2a |
t | 0 | 1 |
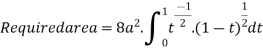
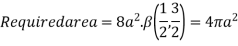
Ex: 2: Show that the area of curve  is
is 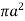
Solution: The curve is symmetrical about Y - axis passing through origin and there exists a cusp at origin. It intersects Y-axis at (0 , 0) , (0 , 2a) .
Also 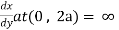 .
.
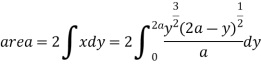
Putting 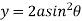
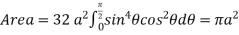 .
.
Ex.3: Find the Area included between the two cardioids 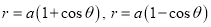
Solution: - Area = 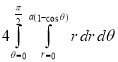
= 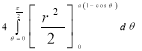
= 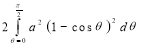
= 
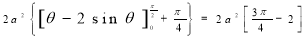
Ex.4: Find the Area common to the two circle 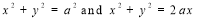
Solution: - By converting the given circle into polar form we get

Area = 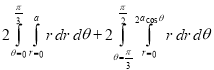
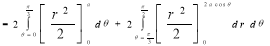
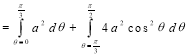

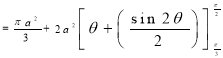
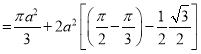

In polar coordinates, we need to evaluate
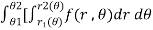
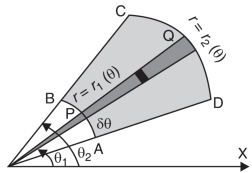
Over the region bounded by θ1 and θ2.
And the curves r1(θ) and r2(θ)
Example-1: Evaluate the following by changing to polar coordinates,

Sol. In this problem, the limits for y are 0 to 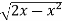 and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 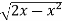
Squaring both sides,
y² = 2x - x²
x² + y² = 2x
But in polar coordinates,
We have,
r² = 2r cosθ
r = 2 cosθ
From the region of integration, r lies from 0 to 2 cosθ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cosθ and y by r sinθ , dy dx by r dr dθ,
We get,
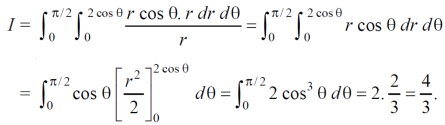
Example-2: Evaluate the following integral by converting into polar coordinates.
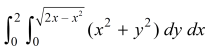
Sol. Here limits of y ,
y = 
y² = 2x - x²
x² + y² = 2x
x² + y² - 2x = 0 ………………(1)
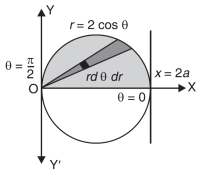
Eq. (1) represent a circle whose radius is 1 and centre is ( 1, 0)
Lower limit of y is zero.
Region of integration in upper hapf circle,
First we will covert into polar coordinates,
By putting
x by r cosθ and y by r sinθ , dy dx by r dr dθ,
Limits of r are 0 to 2 cosθ and limits of θ are from 0 to π / 2.
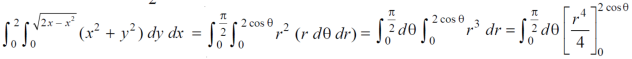

Example-3: Evaluate 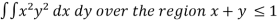
Sol. Let the integral,
I = 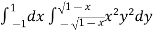
=
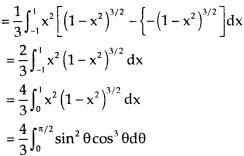
Put x = sinθ
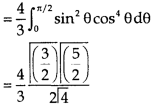
= π / 24 ans.
Area in Cartesian coordinates-
Example-1: Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
Sol. Let,
y = 2 – x ………………..(1)
And y² = 2 (2 – x) ………………..(2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2) ,
We know that,
Area = 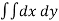
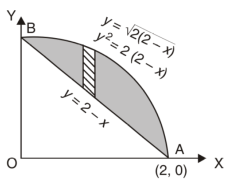
Here we will find the area as below,
Area = 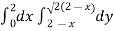
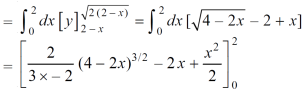
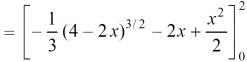
Which gives,
= ( - 4 + 4 /2 ) + 8 / 3 = 2 / 3.
Example-2: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.
Sol. Let,
y ² = 4ax ………………..(1)
And
x² = 4ay…………………..(2)
Then if we solve these equations, we get the values of points where these two curves intersect
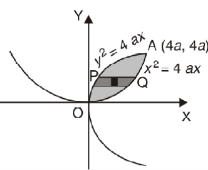
x varies from y²/4a to 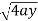 and y varies from o to 4a,
and y varies from o to 4a,
Now using the concept of double integral,
Area = 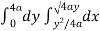
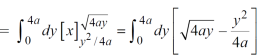
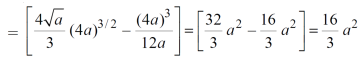
Area in polar coordinates-
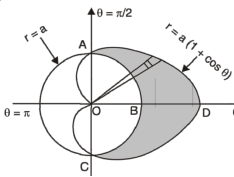
Example-3: Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.
Sol. We have,
r = a(1+cosθ) …………………….(1)
And
r = a ……………………………….(2)
On solving these equations by eliminating r , we get
a(1+cosθ) = a
(1+cosθ) = 1
Cosθ = 0
Here a θ varies from – π/2 to π/2
Limit of r will be a and 1+cosθ)
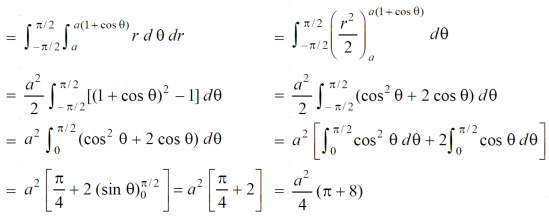
Which is the required area.
Example-4: Find the are lying inside a cardioid r = 1 + cos θ and ouside the parabola r(1 + cos θ) = 1.
Sol. Let,
r = 1 + cos θ ……………………..(1)
r(1 + cos θ) = 1……………………..(2)
Solving these equestions , we get
(1 + cos θ )( 1 + cos θ ) = 1
(1 + cos θ )² = 1
1 + cos θ = 1
Cos θ = 0
θ = ±π / 2
So that, limits of r are,
1 + cos θ and 1 / 1 + cos θ
The area can be founded as below,
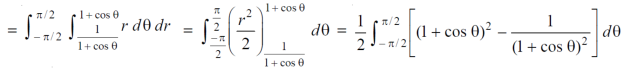

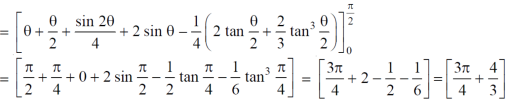
Definition: Let f(x,y,z) be a function which is continuous at every point of the finite region (Volume V) of three dimensional space. Divide the region V into n sub regions of respective volumes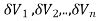 . Let (
. Let (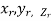 ) be a point in the
) be a point in the 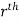 sub region then the sum:
sub region then the sum:
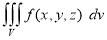 =
= 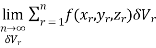
Is called triple integration of f(x, y, z) over the region V provided limit on R.H.S of above Equation exists.
Spherical Polar Coordinates
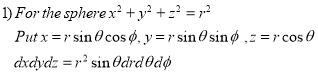
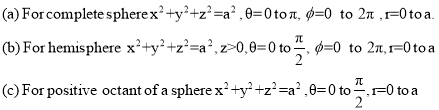
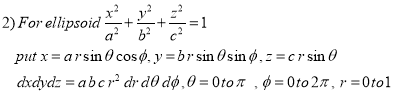
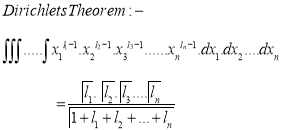
Where the integral is extended to all positive values of the variables subjected to the condition 
Ex.1: Evaluate
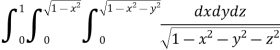
Solution : Let
I = 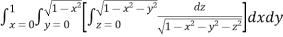
= 
(Assuming m = 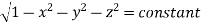 )
)
= 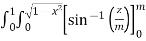 dxdy
dxdy
= 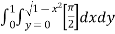
=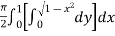
= 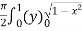 dx
dx
=  dx
dx
= 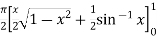
=
I =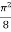
Ex.2: Evaluate 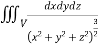 Where V is annulus between the spheres
Where V is annulus between the spheres 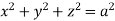
And  (
(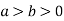 )
)
Solution: It is convenient to transform the triple integral into spherical polar co-ordinate by putting
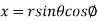 ,
, 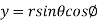 ,
, 
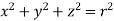 , dxdydz=
, dxdydz= sin
sin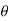 drd
drd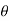 d
d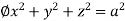 ,
,
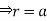 and
and 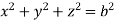
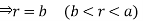
For the positive octant, r varies from r =b to r =a ,  varies from
varies from 
And  varies from
varies from 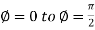
I= 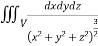
= 8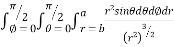
=8
=8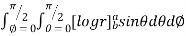
=8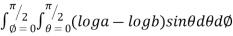
=8 log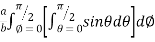
= 8 log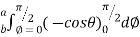
I= 8 log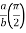 I = 4 log
I = 4 log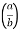
Ex.3: Evaluate 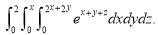
Solution:-
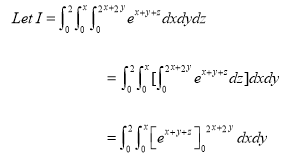
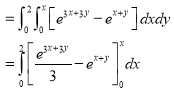
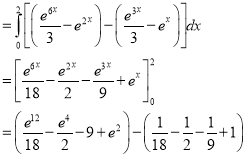
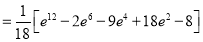
Ex.4:Evaluate 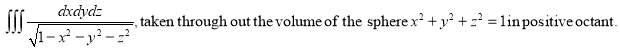
Solution:- 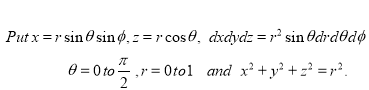
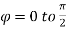
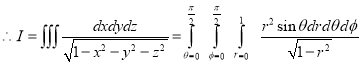
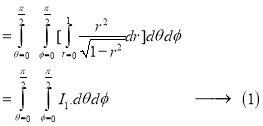
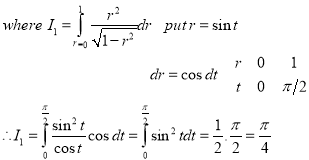
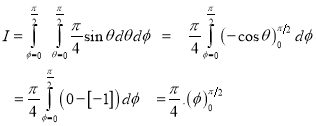
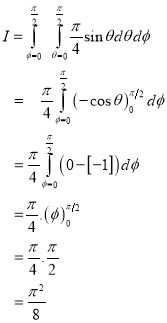
NOTES:
The volume of solid is given by
Volume =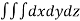
In Spherical polar system
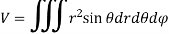
In cylindrical polar system

Ex.1: Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane
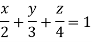
Solution: Volume =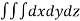 ………. (1)
………. (1)
Put 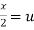 ,
, 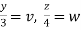

From equation (1) we have
V = 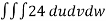
=24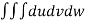
=24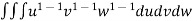 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 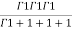
=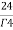 =
=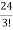 = 4
= 4
Volume =4
Ex.2: Find volume common to the cylinders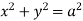 ,
, 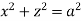 .
.
Solution: For given cylinders,
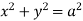 ,
, 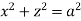 .
.
Z varies from
Z=-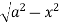 to z =
to z = 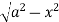
Y varies from
y= -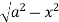 to y =
to y = 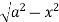
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 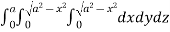
=8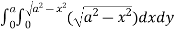
= 8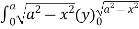 dx
dx
=8
=8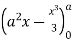
=8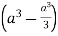
Volume = 16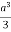
Ex.3: Evaluate
1. 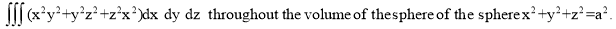 Solution:-
Solution:-
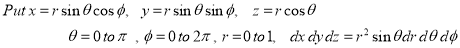
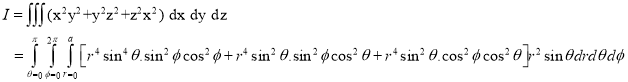
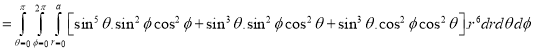
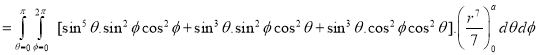
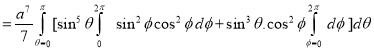
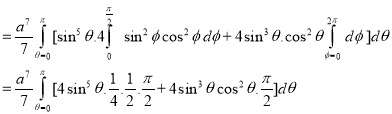
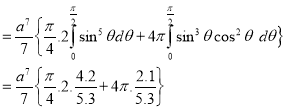
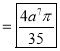
Ex.4: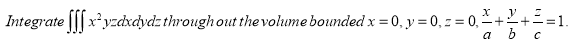
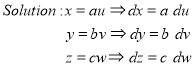
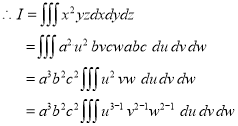
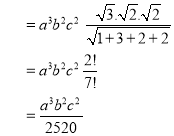
Ex.5: Evaluate 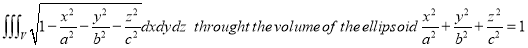
Solution:- Put

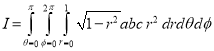
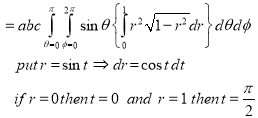
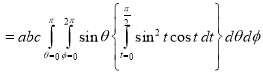

NOTES:
MASS OF A LAMINA :- If the surface density ρ of a plane lamina is a function of the position of a point of the lamina, then the mass of an elementary area dA is ρ dA and the total mass of the lamina is 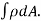
In Cartesian coordinates, if ρ = f(x, y) the mass of lamina, M=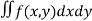
In polar coordinates, if ρ = F(r, Ө) the mass of lamina, M=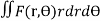
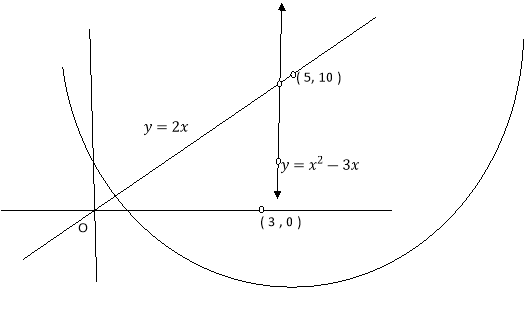
Ex.1: A lamina is bounded by the curves  and
and 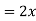 . If the density at any point is
. If the density at any point is  then find mass of lamina.
then find mass of lamina.
Solution:

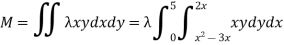
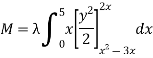
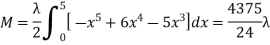
Ex.2:If the density at any point of a non uniform circular lamina of radius’ a’ varies as its distance from a fixed point on the circumference of the circle then find the mass of lamina.
Solution:

Take the fixed point on the circumference of the circle as origin and diameter through it as x axis. The polar equation of circle 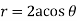
And density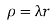 .
.

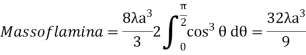
Mean Value:
The mean value of the ordinate y of a function 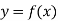 over the range
over the range 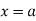 to
to  is the limit of mean value of the equidistant ordinates
is the limit of mean value of the equidistant ordinates 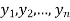 as
as 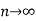
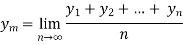
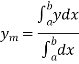
Mean Square values of function 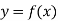 over the range
over the range 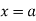 to
to 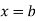 is defined as
is defined as
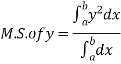
Mean Square values of function 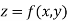
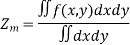
Mean Square values of function 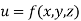
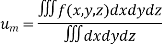
Root Mean Square Value: (R.M.S. Value):
If y is a periodic function of x of period p, the root mean square value of y is the square root of the mean value of 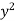 over the range
over the range 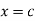 to
to 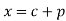 , c is constant.
, c is constant.
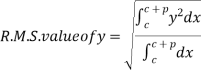
Ex. 1: Find mean value and R.M.S. Value of the ordinate of cycloid
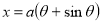 ,
, 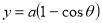 over the range
over the range 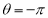 to
to 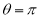 .
.
Sol Let P(x,y) be any point on the cycloid . Its ordinate is y.

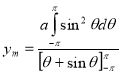
= 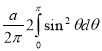
=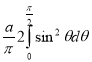
=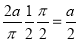
R.M.S.Value= 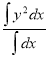
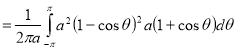

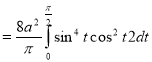


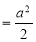
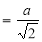
Ex. 2: Find The Mean Value of  Over the positive octant of the
Over the positive octant of the
Ellipsoid 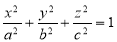
Sol: M.V.=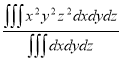
Since 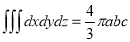
Put 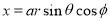
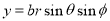
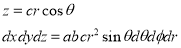
M.V.=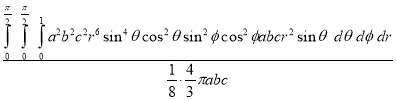

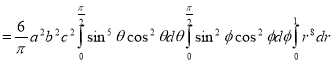
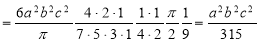
Cartesian coordinate into spherical coordinates-
The relationship between the Cartesian and spherical coordinates is given by,
x = r sinθ cos∅
y = r sinθ sin∅
z = x = r cosθ
Dx dy dz = r² x = r sinθ dr dθ d∅
Example-: Evaluate the following integral throughout the volume of the sphere,
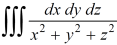
Sol. We are given,
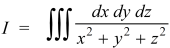
Change the coordinates into spherical coordinates,
Put,
x = r sinθ cos∅
y = r sinθ sin∅
z = x = r cosθ
Dx dy dz = r² x = r sinθ dr dθ d∅
Limits are as below,
Limit of r - 0 to a
Limit of θ = 0 to π/2
Limit of ∅ = 0 to π/2
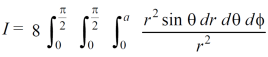
[ the given shere lies in 8th quadrant]
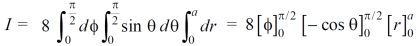
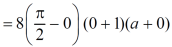
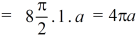
Example: Evaluate the following triple integral over the firsr octant of the sphere x² + y² + z² = a²

Sol. We are given,
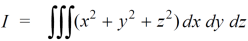
Change the coordinates to spherical,
x = r sinθ cos∅
y = r sinθ sin∅
z = x = r cosθ
Dx dy dz = r² x = r sinθ dr dθ d∅
Limits are as below,
Limit of r - 0 to a
Limit of θ = 0 to π/2
Limit of ∅ = 0 to π/2
Now we can find the integral as below,

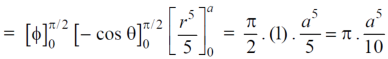
Cartesian coordinates into cylindrical coordinates-
We will change the Cartesian coordinates to cylindrical coordinate as follows-
x = r cos θ
y = r sin θ
z = z
Dx dy dz = r dr dz
Example: Evaluate the triple integral 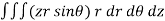 , where the limits of r ,
, where the limits of r , 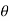 , z are 0≤ r ≤ 2 , 0 ≤ θ ≤ π / 2 and 0 ≤ z ≤ 4.
, z are 0≤ r ≤ 2 , 0 ≤ θ ≤ π / 2 and 0 ≤ z ≤ 4.
Sol. We can use the method of triple integration as follows,
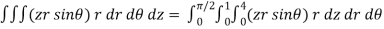
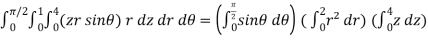
On solving the above integral, it gives
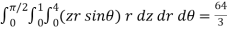
Therefore the value of the integral is 64/3
If u and v be continuous and differentiable functions of two other independent variables x and y such as
 ,
, 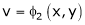 then we define the determine
then we define the determine
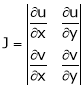 as Jacobian of u, v with respect to x, y
as Jacobian of u, v with respect to x, y
Similarly ,
JJ’ = 1
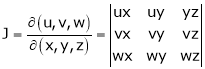
Actually Jacobins are functional determines
Ex.
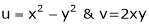 Calculate
Calculate 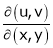
- If
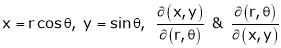
- If
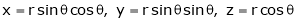
ST 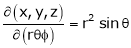
4.  find
find 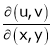
5. If 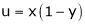 and
and 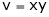 , find
, find 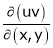
6. 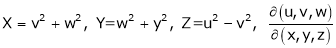
7. If 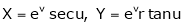
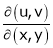
8. If 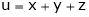 ,
, 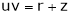 ,
, 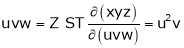
JJ1 = 1
If 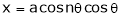 ,
, 
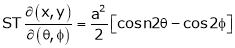
JJ1=1
Jacobian of composite function (chain rule)
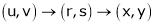
Then 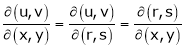
Ex.
- If

Where 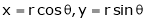
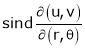
2. If 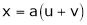
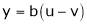 and
and 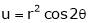
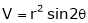
Find 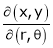
3. If 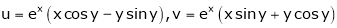
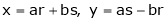
Find 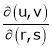
Jacobian of Implicit function
Let u1, u2 be implicit functions of x1, x2 connected by f1, f2 such there
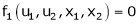 ,
, 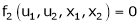
Then 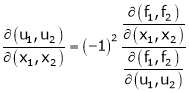
Similarly,
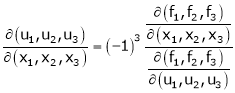
Ex.
If 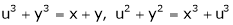
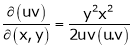
If 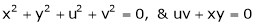
Find 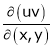
Partial derivative of implicit functions
Consider four variables u, v, x, y related by implicit function.
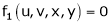 ,
, 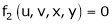
Then
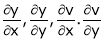
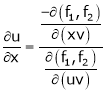
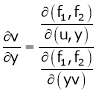
Ex.
If 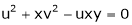 and
and 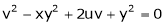
Find 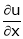
If 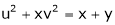 and
and 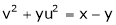
Find 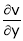
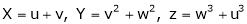
Find 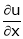
If 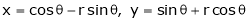
Find 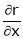
We can solve the double integration by changing the independent variable.
Suppose there is an integral 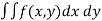
It is to be changed by the new variables u and v.
The relationship between x and y can be given as-
x = ∅( u , v)
y = g(u , v)
Then the double integration can be converted into,
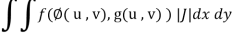
Where,
Dx dy = |J| du dv = 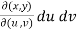 =
=  du dv
du dv
Example; Using the transformation x + y = u and y = uv, find the value of the following double integral , taken over the area of the triangle bounded by the lines x = 0 and y = 0 , x + y = 1.
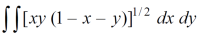
Sol. It is given that,
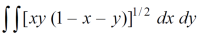
We have,
x + y = u or x = u – y or x = u – uv
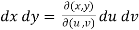 =
= 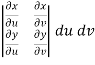

x = 0 ,
u ( 1 – v) = 0
u = 0 , v = 0
y = 0
Uv = 0
u = 0 , v = 0
x+y = 1
u = 1
Therefore the limit of u is from 0 to1 and the limit of v are from 0 to 1.
On putting x = u – uv , y = uv , dx dy = u du dv , we get