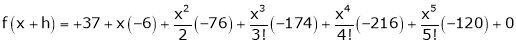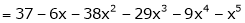Unit – 2
Content
First we will understand the concept of sequence-
Sequence- A sequence <Sn> is said to tend to limit “l” , when given any positive number ‘ϵ’ , however small , we can always find a integer ‘m’ such that | Sn – l| <ϵ , for every for all, n≥m , and we can define this as follows,
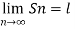
Convergent sequence- A sequence Sn is said to be convergent when it tends to a finite limit. That means the limit of a sequence Sn will be always finite in case of convergent sequence.
Divergent sequence- when a sequence tends to ±∞ then it is called divergent sequence.
Note- a sequence which neither converges nor diverges , is called oscillatory sequence.
A sequence converges to zero Is called null.
Example-1: Show that 
Sol. For ϵ> 0 , we need to find an integer N such that ,
| 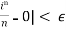
For all n≥N , since |i|=1 we need 1/n<ϵ , so that we choose any N>1 / ϵ>0 , for all n≥N , we find that
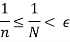
Here |i| = 1 , then
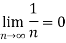
Example-2: consider a sequence 2, 3/2 , 4/3 , 5/4, …….. HereSn = 1 + 1/n
Sol. As we can see that the sequence Sn is convergent and has limit 1.
According to def.
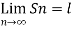

Example-3: consider a sequence Sn= n² + (-1)ⁿ.
Sol. Here we can see that, the sequence Sn is divergent as it has infinite limit.
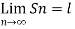

Let {an} , {bn} and {cn} be real sequences such that an ≤ bn≤ cnfor all n . If
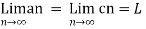
Then
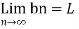
Proof:
The hypotheses says that,
0 ≤ bn – an ≤cn – an , for all n
So that,
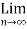 (cn – an ) = L – L = 0
(cn – an ) = L – L = 0
And ,
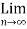 (bn – an ) = 0
(bn – an ) = 0
Thus,
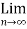 bn=
bn=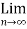 ( bn – an + an)
( bn – an + an)
=  ( bn – an) +
( bn – an) + 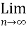 an
an
= 0 + L
= L
This is the proof of Sandwich theorem.
Example-1: show that
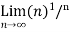 = 1
= 1
Sol.
Let Sn =  - 1 for all n >0 , here Sn≥ 0 for all positive n , therefore
- 1 for all n >0 , here Sn≥ 0 for all positive n , therefore
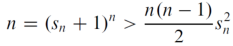
For all n>0 ,
For all n > 1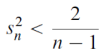

From Sandwich theorem, we get,
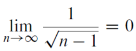
Example-2: show that

For each constant b > 0
Sol.
Lets start with b ≥ 1 and fix an integer, n ≥b .
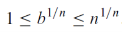
By sandwich theorem ,
For b such that 0< b < 1 , we have 1 / b >1 , hence
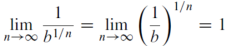
The function f is continuous at a if and only if it satisfies the following property-
For every sequences, {Sn},
If
It says in order to f to be continuous , it is necessary and sufficient that any sequence {Sn} converging to a must force the sequence (f(Sn)) to converges to f(a).
Theorem-1: Let f and g both are continuous at a .then f + g and f.g are continuous at a.
Proof:
Suppose there is sequence {Sn} which converges to ‘a’
Since f is continuous at a , then by the above statement,
 )
)
Similarly,
If g is continuous at a , then

And ,

Similarly we can prove for f.g
Hence proved.
Suppose anbe a sequence then,
1. The sequence is increasing when , an<an+1
2. The sequence is decreasing , when , an >an+1
3. Whenan is increasing sequence or decreasing sequence we call It a monotonic.
4. When there is a number m such that m ≤an for every n we can say that the sequence is bounded below
5. When there is a number m such that m ≥an for every n we can say that the sequence is bounded above.
When a monotonic sequence which is bounded above and bounded below known as bounded monotonic sequence.
For the better understanding , we will do some examples
Example-1: check whether the sequence is bounded monotonic sequence or not.

Sol. This is the decreasing sequence, hence we can say that this is monotonic for every n.
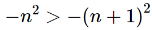
As we can notice here that the terms in this sequence will be either zero or negative , so that the sequence is bounded above.
Suppose m = 0 then,
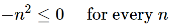
This sequence is not bounded below ,
Hence we can not say that the sequence is bounded.
Example-2: check whether the sequence is bounded monotonic sequence or not.
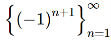
Sol. Here the value of the terms in this sequence will lie between -1 to +1 so the sequence is neither increasing and not decreasing , that means the sequence is not monotonic.
But , it is bounded above by 1 and bounded below by -1, then we can say that the sequence is bounded.
This is divergent sequence too.
Example-3: check whether the sequence is bounded monotonic sequence or not.
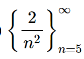
Sol. This is the decreasing sequence , so that the this is a monotonic sequence.
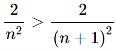
All the terms are positive is this sequence so that it is bounded below by 0.
And the sequence is decreasing , that means the first term will be the largest one.
So that it is bounded above by 2 / 25. ( put n = 5)
Thus we can conclude that the sequence is bounded monotonic equence.
Infinite series- If Un is a sequence , then U1 + U2 + U3 +………………+Un is called the infinite series.
It is denoted by 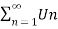 .
.
Examples of infinite series-


Covergent series - suppose n→∞ , Sn→ a finite limit ‘s’ , then the seiresSn is said to be convergent .
We can denote it as,

Divergent series- whenSn tends to infinity then the series is said to be divergent.
Properties of infinite series –
1. The convergence and divergence of an infinite series is unchanged addition od deletion of a finite number of term from it.
2. If positive terms of convergent series change their sign , then the series will be convergent.
3. Let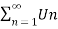 converges to s , let k be a non-zero fixed number then
converges to s , let k be a non-zero fixed number then  converges to ks.
converges to ks.
4. Let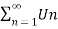 converges to ‘l’ and
converges to ‘l’ and 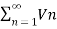 converges to ‘m’.
converges to ‘m’.
Example-1: check whether the series  is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
Sol. As we know that,
Sn = 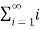
Therefore,
Sn = 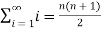
Now find out the limit of the sequence,
 = ∞
= ∞
Here the value of the limit is infinity, so that the series is divergent as sequence diverges.
Example-2: check whether the series  is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
Sol. The general formula for this series is given by,
Sn = 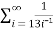 =
= 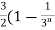 )
)
We get,
 ) = 3/2
) = 3/2
Hence the series is convergent and its values is 3/2.
Example-3: check whether the series 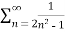 is convergent or divergent.
is convergent or divergent.
Sol. The general formula can be written as,
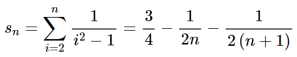
We get on applying limits,
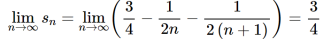
This is the convergent series and its value is 3 / 4
Suppose there are infinite series having infinite number of terms such as,
s1 = a1
s2 = a1 + a2
s3 = a1 + a2 + a3
s4 = a1 + a2 + a3 + a4
s5 = a1 + a2 + a3 + a4 + a5
……………………………
……………………………..
Sn = a1 + a2 + a3 + a4 + a5 + ………..+ an = 
Sn is called the sum of all series if we combine them.
Here {Sn} is the sequence
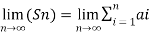 =
= 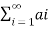
 this is called the infinite series , that starts with i = 1
this is called the infinite series , that starts with i = 1
A series 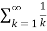 is called harmonic series. This series can be proved divergent by using integral test.
is called harmonic series. This series can be proved divergent by using integral test.
Progression of the series can be represented by,
Example-1: show that the following series  is divergent
is divergent
Sol. To prove this series divergent , we follow the steps below,

As we know that 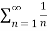 will always diverge.
will always diverge.
And if we multiply a divergent series with a constant then the resulting series will also be divergent.
Hence we can say that theeries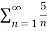 will be divergent.
will be divergent.
Example-2: Show that the harmonic series  is divergent.
is divergent.
Sol. First we will expand its three terms ,
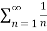 = 1+
= 1+  +
+ 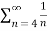
We get,

Here if we subtract a finite number from a divergent series , then the resulting series will not be affected by this number.
Therefore we can say that  is the divergent series which is also a harmonic series.
is the divergent series which is also a harmonic series.
A positive term series
∅(1) + ∅(2) +∅(3) + ∅(4)+ …………..∅(n) + ………
Where ∅(n) decreases as n increases , is convergent or divergent according as the integral 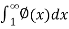 is finite or infinite.
is finite or infinite.
Proof: suppose, Sn = ∅(1) + ∅(2) +∅(3) + ∅(4)+ …………..∅(n)
Here n = 1,2,3,4,………n , n+1, ……..
Hence the total area under the curve ( see fig) lies between the sum of areas of all interior rectangles and sum of the area of all exterior rectangles
So that,



As n tends to infinity , then limit of Sn will be finite or infinite according as 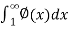 is finite or infinite.
is finite or infinite.
Example-1: determine the following series is convergent or divergent.

Sol. By using integral test
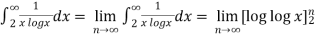 = ∞
= ∞
By the integral test, given series is divergent as 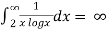
Example-2: Test the series by integral test- 
Sol. Here 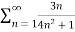 is positive and decreases when we increase n ,
is positive and decreases when we increase n ,
Now apply integral test,
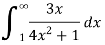
Let,

X = 1 , t = 5 and x = ∞ , t = ∞,
Now,

So by integral test,
The series is divergent.
Example-3: Test the series by integral test- 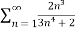
Sol. Here 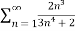 decreases as n increases and it is positive.
decreases as n increases and it is positive.
By using integral test,
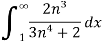
= 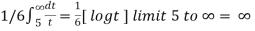
We get infinity,
So that the series is divergent.
The infinite series,
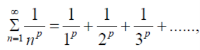
Is convergent , when
(1) convergent when p >1
(2) divergent if p <= 1
Proof;
Let p>1

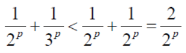
Similarly,

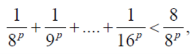
And so on.
Adding we get,
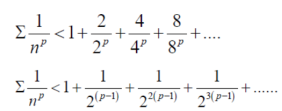
The right hand side of the above inequality is an infinite geometric series , the sum of the geometric series is finite hence the given series is convergent.
Example-1: Test the convergence of the following series:
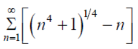
Sol.
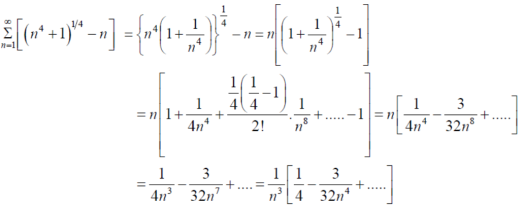
Here we take,
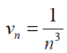
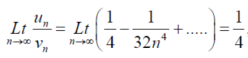
Which not zero and finite ,
So by comparison test ,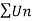 and
and 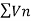 both converges or diverges, but by p-series test
both converges or diverges, but by p-series test
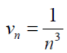
Is convergent .so that 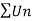 is convergent.
is convergent.
Example-2: Test the convergence of the given series:
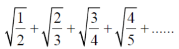
Sol. Here,

Take,

 is divergent by p-series test. (p = 0 <1)
is divergent by p-series test. (p = 0 <1)
Example-3: Test the convergence of the series:
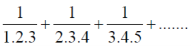
Sol.

By p-series test,
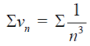
Is convergent ( p = 3>1).
Let ,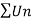 and
and 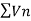 be two series of positive terms and let
be two series of positive terms and let 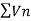 be convergent ,
be convergent ,
Then , converges ,
converges ,
1. If,

Or
2.
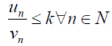
Or
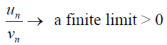
Example: Show that the following series is convergent.
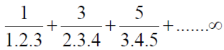
Sol.
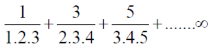

Suppose,

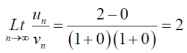
Which is finite and not zero.
By comparison test 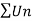 and
and 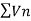 converge or diverge together.
converge or diverge together.
But,

Is convergent. So that  is also convergent.
is also convergent.
Example: Test the series:
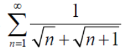
Sol. The series is,
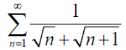
Now,

Take,

Which is finite and not zero.
Which is finite and not zero.
By comparison test  and
and  converge or diverge together.
converge or diverge together.
But,
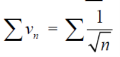
Is divergent. ( p = ½)
So that 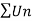 is divergent.
is divergent.
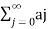 and
and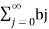
Be the series of positive terms.
Then
1. Both series converge or diverge for –
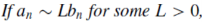
2. The series converges if –
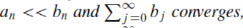
3. Diverges for-
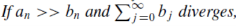
Example: Test the convergence of the series:
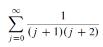
Sol. Let
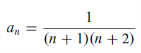
For all n> 0we show that An has the same order of magnitude as 1/n².
We put accordingly
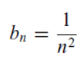
For all n>0, then
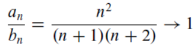
As n tends to infinity , thus
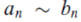
Then the series converges by limit comparison rule.
Example: Test the series for convergence.
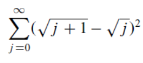
Sol. For all n>= 0 let,
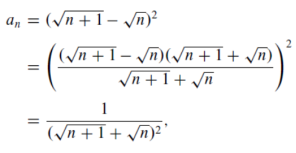
And let,
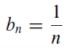
For all n>0, since

It follows,
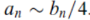
By limit comparison test , the series is divergent
Example: Test the series
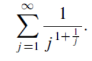
Sol. Take,
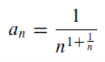
And,

For all n>0, we get
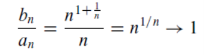
Thid is a divergent series.
Let 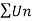 be a series of positive terms and
be a series of positive terms and
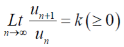
Then , the series,
(1) is convergent if k < 1
(2) is divergent if k>1
Proof:
Case-1:

We know that from the definition of limits ,it follows,
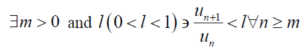

But,

Is the finite quantity. So  is convergent.
is convergent.
Case-2:

There could be some finite terms in starting which will never satisfy the condition,
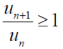
In this case we can find a number ‘m’,
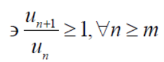
Ignoring the first ‘m’ terms, if we write the series as
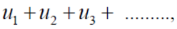
We have , in this case
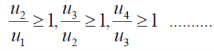



So that 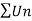 is divergent.
is divergent.
Let 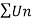 be a series of positive terms and
be a series of positive terms and

Then,
(1) if k >1 ,  is convergent and
is convergent and
(2) if k < 1 , then  is divergent
is divergent
(3) this test fails if k = 1.
Proof: let us consider the series,
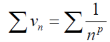

Case-1: in this case,
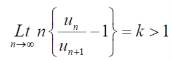
We choose a number ‘p’ for all k > p >1 , comparing thr series  with
with 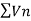 which is divergent ,
which is divergent ,
We get  will converge if after some fixed numver of terms ,
will converge if after some fixed numver of terms ,

That means,
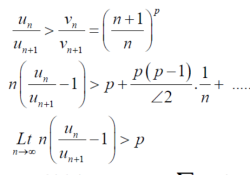
If k >p , which Is true . Hence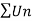 is convergent.
is convergent.
We can prove the second case similarly.
Example-1: Test the convergence of the following series.
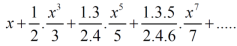
Sol. Neglecting the first term the series can be written as,

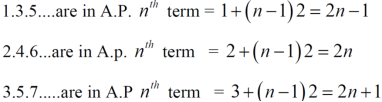
So that,
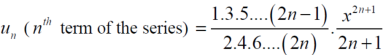

By ratio test  converges if |x|<1 and diverges if |x|>1, but if |x| = 1 the the test fails,
converges if |x|<1 and diverges if |x|>1, but if |x| = 1 the the test fails,
Then ,

By Raabes’s test 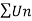 converges hence the given series is convergent when |x|≤ 1 and divergent If |x| >1.
converges hence the given series is convergent when |x|≤ 1 and divergent If |x| >1.
Example-2: Test the convergence of the series,
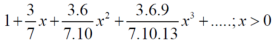
Sol. As we will neglect the first term, we get

By ration test 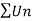 is convergent when x<1 and divergent when x>1, when x= 1,
is convergent when x<1 and divergent when x>1, when x= 1,
The rario test fails, then
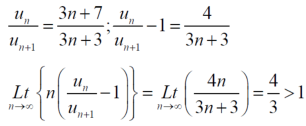
By Rabee’s test 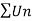 is convergent , hence the given series is convergent when x≤ 1 and divergent If x >1.
is convergent , hence the given series is convergent when x≤ 1 and divergent If x >1.
Example-3: Test the nature of the following series:
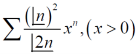
Sol.
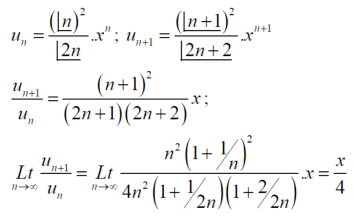
By ration test 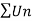 is convergent when (x/4)<1 and divergent when x>4, when x= 4,
is convergent when (x/4)<1 and divergent when x>4, when x= 4,
The rario test fails, then

By Rabee’s test 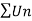 is convergent , hence the given series is convergent when x<4 and divergent If x >=4.
is convergent , hence the given series is convergent when x<4 and divergent If x >=4.
Let 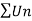 be a series of positive terms and let
be a series of positive terms and let
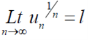
Then  is convergent when l<1 and diverges when l >1.
is convergent when l<1 and diverges when l >1.
Proof: case-1:
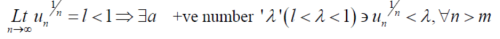
Or
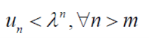
Since,
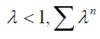
Is a geometric series with common ratio <1 so that the series will be convergent.
Case- 2:
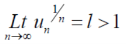
By the limit concept, we can find a number,
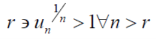
That means
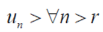
After 1st ‘r’ terms , each term is > 1
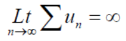
So that the series is divergent.
Example: Test the convergence of the series whose nth term is given below-

Sol.
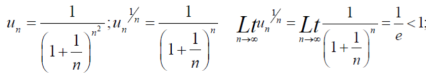
By root test  is convergent.
is convergent.
Example: Test the convergence of the series whose nth term is given below-
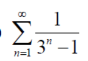
Sol.
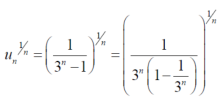
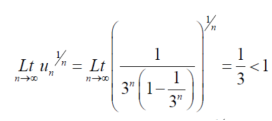
By root test 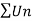 is convergent.
is convergent.
Example: show that the following series is convergent.
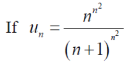
Sol.

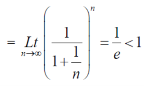
By root test 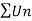 is convergent.
is convergent.
Definition- the series,
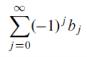
Is alternating if each bj is positive.
Test- the alternating series is convergent if {bn} is a non – increasing sequence of positive terms converging to zero.
Proof: for each integer , n ≥ 0, let
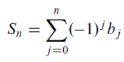
We need to show that the sequence {Sn} converges. We will do this as follows
First we have,
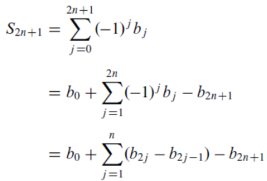
Note
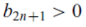
Here
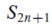
Is bounded above b0, it is non- decreasing because for all n>0, we have
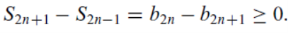
Which is the proof.
A series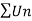 is said to be absolutely convergent if the series
is said to be absolutely convergent if the series  is convergent.
is convergent.
For example- suppose the following series,
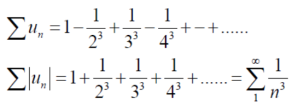
By p- series test, we can say that  is convergent.
is convergent.
Hence 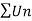 is absolutely convergent.
is absolutely convergent.
Note- if the series has positive terms and it is convergent then this series will be absolutely convergent too.
An absolute convergent series will be convergent but the converse may not be true.
Conditional convergence-:
If the series 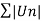 is divergent and
is divergent and 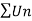 is convergent then
is convergent then 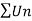 is aid to be conditionally convergent
is aid to be conditionally convergent
Example: Test the series for absolute/conditional convergence.
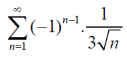
Sol. The given series is an alternating series of the form,

Here,
1.
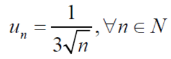
2.
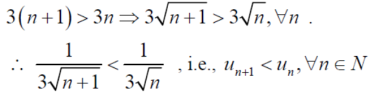
And,
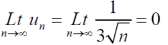
Hence bt Leibnitz’s test , the given series is convergent ,
But,

Is divergent by p-series test.
So that, the given series is conditionally convergent.
Example: Test for the convergence of the series:
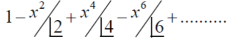
Sol. The given series is,
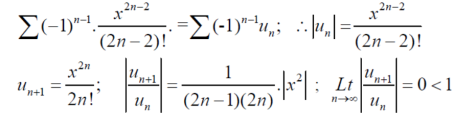
By ratio test series 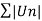 converges, so that the series is convergent.
converges, so that the series is convergent.
Example: Test for absolute convergence:

Sol. Let the series is  ,
,

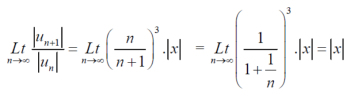
By ratio test,
 is convergent , if |x|<1.
is convergent , if |x|<1.
 is absolutely convergent if |x|< 1.
is absolutely convergent if |x|< 1.
A series
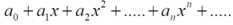
Where An are all the constant is a power series in x.
It may converges for some values of x,

We neglect first term here,
Suppose it is equals to kx,
Where,
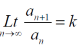
By ratio test, the series converges, when |kx|<1
That means it converges
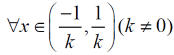
The interval ( -1 /k , 1/k) is known as the interval of convergence of the power series.
Example: Find the interval of convergence.
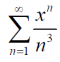
Sol.
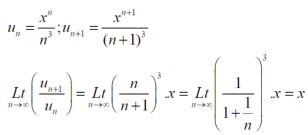
We can see that, by ratio test , the given series converges when |x|<1
That means x = (-1,1)
When x = 1
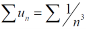
Which is convergent by p-series test.
The interval of convergence of the given series is (-1,1).
A power series is a variable z is defined as a series of the form
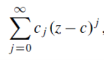
The power series converges absolutely for all z , it converges only when z = c , or there exists a positive number ‘r’ such that the power series converges absolutely if |z – c|< r, and diverges if |z-c|>r ,
Then the ‘r’ is called the radius of convergence of a power series.
Example : Find the radius of convergence for the power series,
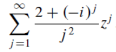
Sol. Set,

For each n>0.
If |z|<=1, then |a|<= 3/n²
Since

Converges the given series is absolutely convergent by the comparison test. Suppose therefore |z|>1
Since,

For all n>0, the sequence does not converges to 0 and the series diverges .
Hence the radius of the convergence is 1.
Expand by Maclaurin’s theorem,
Log sec x
Solution:
Let f(x) = log sec x
 By Maclaurin’s Expansion’s,
By Maclaurin’s Expansion’s,
 (1)
(1)

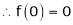
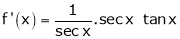



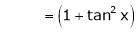
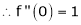

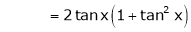
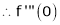



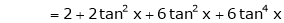


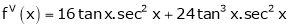
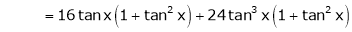
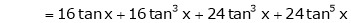
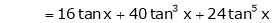
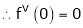
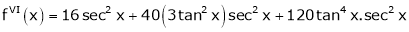
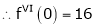
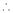 By equation (1)
By equation (1)

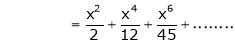
Prove that 
Solution:
Here f(x) = x cosec x
= 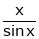
Now we know that

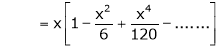
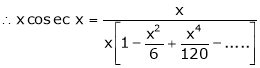
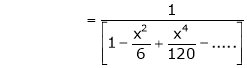

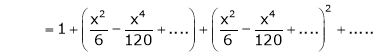
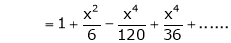

Expand 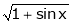 upto x6
upto x6
Solution:
Here 

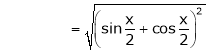

Now we know that
 … (1)
… (1)
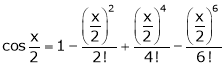 … (2)
… (2)
Adding (1) and (2) we get
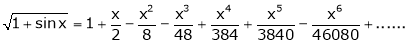
Show that 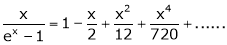
Solution:
Here 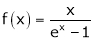
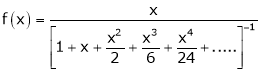
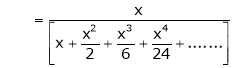
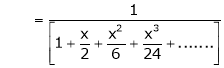

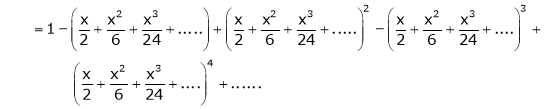
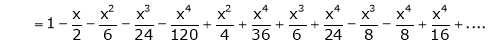
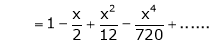
Thus
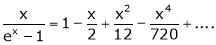
Taylor’s Series Expansion:-
a) The expansion of f(x+h) in ascending power of x is
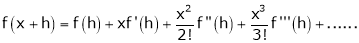
b) The expansion of f(x+h) in ascending power of h is

c) The expansion of f(x) in ascending powers of (x-a) is,
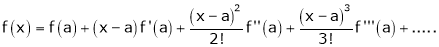
Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions
Expand 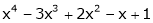 in power of (x – 3)
in power of (x – 3)
Solution:
Let 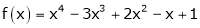
Here a = 3
Now by Taylor’s series expansion,
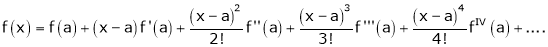 … (1)
… (1)
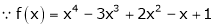
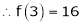


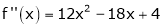
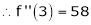

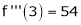
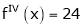
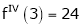
 equation (1) becomes.
equation (1) becomes.
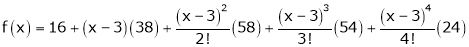
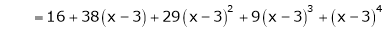
Using Taylors series method expand
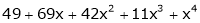 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 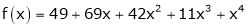
a = -2
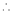 By Taylors series,
By Taylors series,
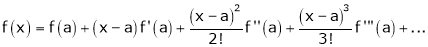 … (1)
… (1)
Since
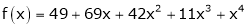


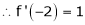
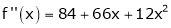

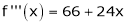
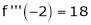

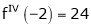 ,
, 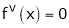 , …..
, …..
Thus equation (1) becomes
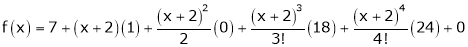
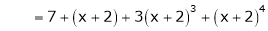
Expand  in ascending powers of x.
in ascending powers of x.
Solution:
Here
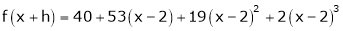
i.e. 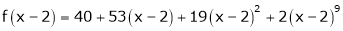
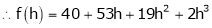
Here h = -2
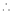 By Taylors series,
By Taylors series,
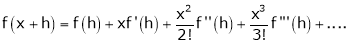 … (1)
… (1)
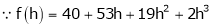
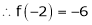
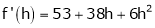
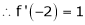
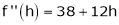
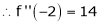
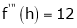
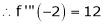

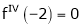
 equation (1) becomes,
equation (1) becomes,
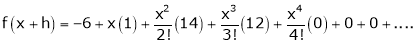

Thus

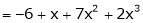
Expand 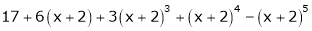 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
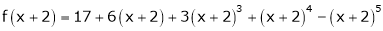
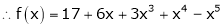
i.e. 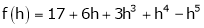
Here
h = 2
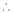 By Taylors series
By Taylors series
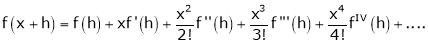 … (1)
… (1)
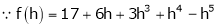
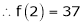
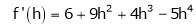
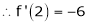


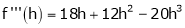
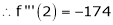
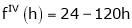
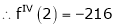


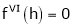
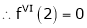
 By equation (1)
By equation (1)