Unit 3
Properties of gases
Content:
Gases are complicated. They're full of billions and billions of energetic gas molecules that can collide and possibly interact with each other. Since it's hard to exactly describe a real gas, people created the concept of an Ideal gas as an approximation that helps us model and predict the behaviour of real gases. The term ideal gas refers to a hypothetical gas composed of molecules which follow a few rules:
Ideal gas molecules do not attract or repel each other. The only interaction between ideal gas molecules would be an elastic collision upon impact with each other or an elastic collision with the walls of the container.
Ideal gas molecules themselves take up no volume. The gas takes up volume since the molecules expand into a large region of space, but the Ideal gas molecules are approximated as point particles that have no volume in and of themselves.
There are no gases that are exactly ideal, but there are plenty of gases that are close enough that the concept of an ideal gas is an extremely useful approximation for many situations. In fact, for temperatures near room temperature and pressures near atmospheric pressure, many of the gases we care about are very nearly ideal.
An ideal gas can be characterized by three state variables: absolute pressure (P), volume (V), and absolute temperature (T). The relationship between them may be deduced from kinetic theory and is called the
Ideal gas law: PV = nRT = NkT
- n = number of moles
- R = universal gas constant = 8.3145 J/mol K
- N = number of molecules
- k = Boltzmann constant = 1.38066 x 10-23 J/K = 8.617385 x 10-5 eV/K
- k = R/NA
- NA = Avogadro's number = 6.0221 x 1023 /mol
Boyle’s law is a gas law which states that the pressure exerted by a gas (of a given mass, kept at a constant temperature) is inversely proportional to the volume occupied by it. In other words, the pressure and volume of a gas are inversely proportional to each other as long as the temperature and the quantity of gas are kept constant. Boyle’s law was put forward by the Anglo-Irish chemist Robert Boyle in the year 1662.
For a gas, the relationship between volume and pressure (at constant mass and temperature) can be expressed mathematically as follows.
P ∝ (1/V)
Where P is the pressure exerted by the gas and V is the volume occupied by it. This proportionality can be converted into an equation by adding a constant, k.
P = k*(1/V) ⇒ PV = k
The pressure v/s volume curve for a fixed amount of gas kept at constant temperature is illustrated below.
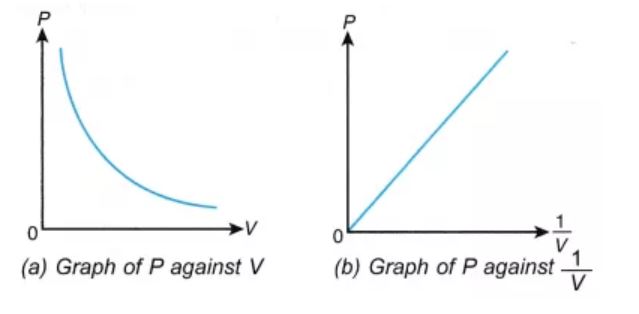
It can be observed that a straight line is obtained when the pressure exerted by the gas (P) is taken on the Y-axis and the inverse of the volume occupied by the gas (1/V) is taken on the X-axis.
Formula and Derivation
As per Boyle’s law, any change in the volume occupied by a gas (at constant quantity and temperature) will result in a change in the pressure exerted by it. In other words, the product of the initial pressure and the initial volume of a gas is equal to the product of its final pressure and final volume (at constant temperature and number of moles). This law can be expressed mathematically as follows:
P1V1 = P2V2
Where,
- P1 is the initial pressure exerted by the gas
- V1 is the initial volume occupied by the gas
- P2 is the final pressure exerted by the gas
- V2 is the final volume occupied by the gas
This expression can be obtained from the pressure-volume relationship suggested by Boyle’s law. For a fixed amount of gas kept at a constant temperature, PV = k. Therefore,
P1V1 = k (initial pressure * initial volume)
P2V2 = k (final pressure * final volume)
∴ P1V1 = P2V2
This equation can be used to predict the increase in the pressure exerted by a gas on the walls of its container when the volume of its container is decreased (and its quantity and absolute temperature remain unchanged)
Charles’ law is one of the gas laws which explain the relationship between volume and temperature of a gas. It states that when pressure is held constant, the volume of a fixed amount of dry gas is directly proportional to its absolute temperature. When two measurements are in direct proportion then any change made in one of them affects the other through direct variation. Charles’ Law is expressed by the equation:
VαT
Or
V1 / T1=V2 / T2
Where,
V1 and V2 are the Initial Volumes and Final Volume respectively. T1 refers to the Initial Temperature and T2 refers to the Final Temperature. Both the temperatures are in the units of Kelvin.
Jacques Charles, a French scientist, in 1787, discovered that keeping the pressure constant, the volume of a gas varies on changing its temperature. Later, Joseph Gay-Lussac, in 1802, modified and generalized the concept as Charles’s law. At very high temperatures and low pressures, gases obey Charles’ law.
Derivation:
Charles’ Law states that at constant pressure, the volume of a fixed mass of a dry gas is directly proportional to its absolute temperature. We can represent this using the following equation:
VαT
Since V and T vary directly, we can equate them by making use of a constant k.
V / T=constant=k
Let V1 and T1 be the initial volume and temperature of an ideal gas. We can write equation I as:
V1 / T1= k ———– (I)
Let’s change the temperature of the gas to T2. Consequently, its volume changes to V2. So, we can write,
V2 / T2=k ———– (II)
Equating equations (II) and (III),
V1 / T1=V2 / T2=k
Hence, we can generalize the formula and write it as:
(V1) / (T1)=(V2) / (T2)
Or
V1T2=V2T1
On heating up a fixed mass of gas, that is, increasing the temperature, the volume also increases. Similarly, on cooling, the volume of the gas decreases.
Charles’ Law in Real Life:
Charles’ law has a wide range of applications in our daily life. Some of the common examples are given below:
- In cold weather or environment, balls and helium balloons shrink.
- In bright sunlight, the inner tubes swell up.
- In colder weather, the human lung capacity will also decrease. This makes it more difficult to do jogging or athletes to perform on a freezing winter day.
The combined gas law is the law which combines Charles’s law, Gay-Lussac’s law and Boyle’s law. It’s an amalgamation of the three previously discovered laws. These laws relate one thermodynamic variable to another holding everything else constant. The interdependence of these variables represents combined gas law which states that the ratio between the product of pressure-volume and temperature of a system remains constant.
Combined Gas Law Formula
Combined gas law can be mathematically expressed as
k = PV/T
Where,
P = pressure
T = temperature in kelvin
V = volume
K = constant (units of energy divided by temperature)
When two substances are compared in two different conditions, the law can be stated as,
PiVi/Ti = PfVf/Tf
Where,
Pi = initial pressure
Vi = initial volume
Ti = initial temperature
Pf = final pressure
Vf= final volume
Tf = final temperature
When the molecular mass of any gas is multiplied by its specific gas constant (R), it is observed that the product R is always the same for all gases. This product is called universal gas constant and it is denoted as R.
From the SI system the value of the universal gas constant is 8.314 kJ/mole.K
Let us consider the pressure exerted by the gas to be p
The volume of the gas be v
Temperature be T
n be the number of moles of gas
Universal gas constant R
According to Boyle’s Law,
At constant n & T, the volume bears an inverse relation with the pressure exerted by a gas.
v ∝ 1/ p ………………………………(i)
According to Charles’ Law,
When p & n are constant, the volume of a gas bears a direct relation with the Temperature.
v ∝ T …………………………(ii)
According to Avogadro’s Law,
When p & T are constant, then the volume of a gas bears a direct relation with the number of moles of gas.
v ∝ n …………………………(iii)
Combining all the three equations, we have-
v ∝ n T / p
p.v=nRT
Where R is the Universal gas constant, which has a value of 8.314 J/mol-K
When heat is absorbed by a body the temperature of the body increases and when heat is lost, the temperature decreases. The temperature of an object is the measure of the total kinetic energy of the particles that make up that object. So, when heat is absorbed by an object this heat gets translated into the kinetic energy of the particles and as a result the temperature increases. Thus, the change in temperature is proportional to the heat transfer.
The formula q = n C ∆T represents the heat q required to bring about a ∆T difference in temperature of one mole of any matter. The constant C here is called the molar heat capacity of the body. Thus, the molar heat capacity of any substance is defined as the amount of heat energy required to change the temperature of 1 mole of that substance by 1 unit. It depends on the nature, size, and composition of the system.
- The molar heat capacity C, at constant pressure, is represented by CP.
- At constant volume, the molar heat capacity C is represented by CV.
The relationship between CP and CV for an Ideal Gas
From the equation q = n C ∆T, we can say:
At constant pressure P, we have
qP = n CP∆T
This value is equal to the change in enthalpy, that is,
qP = n CP∆T = ∆H
Similarly, at constant volume V, we have
qV = n CV∆T
This value is equal to the change in internal energy, that is,
qV = n CV∆T = ∆U
We know that for one mole (n=1) of an ideal gas,
∆H = ∆U + ∆(pV) = ∆U + ∆(RT) = ∆U + R ∆T
Therefore, ∆H = ∆U + R ∆T
Substituting the values of ∆H and ∆U from above in the former equation,
CP∆T = CV∆T + R ∆T
CP = CV + R
CP – CV = R
Constant volume (Isochoric process):
Suppose a gas enclosed in a rigid vessel is interacting with the surroundings and absorbs energy Q as heat. Since the vessel is rigid, the work done W due to expansion or compression is zero. Applying the first law, we get
DU = dQ or Q = U2 –U1
That is, heat interaction is equal to the change in internal energy of the gas. If the system contains a mass m equal of an ideal gas, then
Q = ΔU = mCv (T2 –T1)
The path followed by the gas is shown on a P-V diagram. Now consider the fluid contained in a rigid vessel as shown. The vessel is rigid and insulated. Shaft work is done on the system by a paddle wheel as shown in Fig. a. In Fig. b electric work is done on the system. Since the vessel is rigid, the PdV work is zero. Moreover, the vessel is insulated and hence dQ = 0. Application of the first law of thermodynamics gives
DU = dQ – dW = dQ – (dWpdv + dWs)
Or dU = -dWs or – Ws = ΔU = U2 –U1
Where dWpdv is the compression /expansion work and dWs is the shaft work. That is increase in internal energy of a system at a constant volume, which is enclosed by an adiabatic wall, is equal to the shaft work done on the system.
Constant pressure (Isobaric process):
Several industrial processes are carried out at constant pressure. A few examples of constant pressure processes are: (a) reversible heating/cooling of a gas (b) phase change (c) paddle wheel work (d) electrical work. For a constant pressure process, the work done W is given by
W = ∫PdV = P (V2-V1)
Application of the first law of thermodynamics gives
DU = dQ – dW
= dQ – PdV
= dQ – d (PV)
Or dQ = dU + d (PV) = d(U + PV) = dH
Or Q = ΔH
That is in a constant pressure process, the heat interaction is equal to the increase in the enthalpy of the system. Now consider the constant pressure processes in which the system is enclosed by an adiabatic boundary. Application of the first law gives:
DU = dQ – dW = dQ – (PdV + dWs)
Here, the net work done (dW) consists of two parts – the PdV work associated with the motion of the boundary and (-dWs), the shaft work (or electrical work) done by the surroundings. Since the system is enclosed by an adiabatic boundary, dQ = 0 the equation can be written as
-dWs = dU + d (PV) = dH
That is, the increase in the enthalpy of the system is equal to the shaft work done on the system.
Constant temperature
Suppose a gas enclosed in the piston cylinder assembly is allowed to expand from P1 to P2 while the temperature is held constant. Then application of the first law gives:
DU = dQ – dW = dQ –PdV
It is not possible to calculate work and heat interactions unless the relationships between the thermodynamic properties of the gas are known. Suppose the gas under consideration is an ideal gas (which follows the relation Pv = RT and u =u (T) only) then for an isothermal process,
DU = 0
DQ = PdV = R.T.dv /v or Q =W = RTln(v2/v1)
Adiabatic process:
Reversible adiabatic process is also called an Isentropic Process. It is an idealized thermodynamic process that is adiabatic and in which the work transfers of the system are frictionless; there is no transfer of heat or of matter and the process is reversible. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes.
Adiabatic process derivation
The adiabatic process can be derived from the first law of thermodynamics relating to the change in internal energy dU to the work dW done by the system and the heat dQ added to it.
DU =dQ-dW
DQ =0 by definition
Therefore, 0=dQ=dU +dW
The word done dW for the change in volume V by dV is given as PdV.
The first term is specific heat which is defined as the heat added per unit temperature change per mole of a substance. The heat that is added increases the internal energy U such that it justifies the definition of specific heat at constant volume is given as:
Cv =dUdT1n
Where,
N=number of moles
Therefore, 0= nCvdT+PdV …..(eq.1)
From the ideal gas law, we have
NRT =PV …..(eq.2)
Therefore, nRdT = PdV+VdP…. (eq.3)
By combining the equation 1. And equation 2, we get
−PdV= nCvdT = Cv / R (PdV+VdP)
0 = (1+Cv / R) PdV+Cv / RVdP
0= R+ Cv / Cv (dV / V) +dP /P
When the heat is added at constant pressure Cp, we have
Cp=Cv +R
0=γ (dV / V) +dP / P
Where the specific heat ɣ is given as:
γ ≡ Cp /Cv
From calculus, we have,
d (lnx)=dx / x
0=γd (lnV) + d (lnP)
0=d (γlnV+lnP) =d (lnPVγ)
PVγ=constant
Hence, the equation is true for an adiabatic process in an ideal gas.
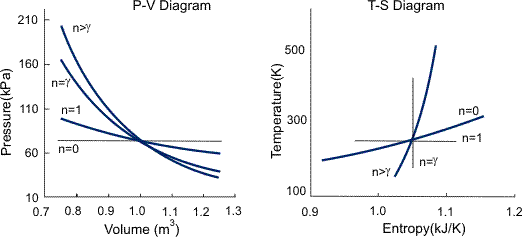
Polytrophic process:
The term "polytropic" was originally coined to describe any reversible process on any open or closed system of gas or vapour which involves both heat and work transfer, such that a specified combination of properties were maintained constant throughout the process. In such a process, the expression relating the properties of the system throughout the process is called the polytropic path.
There are an infinite number of reversible polytropic paths between two given states; the most commonly used polytropic path is
T (dS/dT) = C1…..i
Where T is Temperature, S is Entropy, and C1 is a constant and is equal to zero for an adiabatic process. This path is equivalent to the assumption that the same amount of heat is transferred to the system in each equal temperature increment. In a reversible process following this polytropic path the heat and work transfer are as follows:
Q = C1 (T2-T1)…ii
And W = (H2-H1)-Q….iii
Where H is Enthalpy.
Pressure and volume, and pressure and temperature are related by the following expressions:
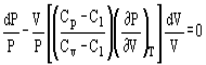
And

Where Cp and Cv are heat capacity at constant pressure and volume, respectively.
For an ideal gas this polytrophic path simplifies to
P.Vn=C2
Where C2 and n are constants and n is called the polytrophic index. The polytrophic index characterizes the process, as summarized and is given by
n = (Cp-C1) / (Cv-C1)
The equivalent pressure temperature and work relationships are as follows:
P (n-1)/n /T = C3 (NR/C21/n)
And
W=n/n-1 (P2V2-P1V1)
Many gas compression and expansion processes may be usefully approximated by a polytropic process. In each case the polytropic coefficient must be determined experimentally by measurement of the heat and work transfer and the initial and final states.
Belt, Rowlinson, and Saville (1975) discuss the errors and inconsistencies which may arise when PVn = C2 is applied to non-ideal gases and vapours.