UNIT 3
PARTIAL DIFFERENTIATION 2
Jacobians
If u and v be continuous and differentiable functions of two other independent variables x and y such as
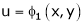 ,
, 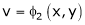 then we define the determine
then we define the determine
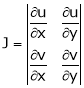 asJacobian of u, v with respect to x, y
asJacobian of u, v with respect to x, y
Similarly ,
JJ’ = 1
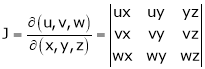
Example 1:
Let x(u,v) = u2 – v2, y(u,v)=uv.find the jacobain j(u,v).
Solution:
Given that x(u,v) =u2-v2 and y(u,v)= 2uv
We know that,
J(u,v)= 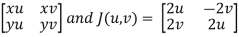
Therefore, J(u,v) = 4u2+4v2
Example 2:
Find 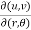 if u= 2xy, v= x2 – y2 and x = r.cos
if u= 2xy, v= x2 – y2 and x = r.cos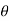 , y = r.sin
, y = r.sin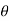
Solution:
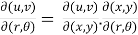
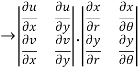
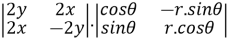
= 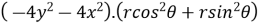
= 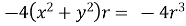
Actually Jacobins are functional determines
Ex.
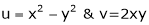
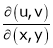
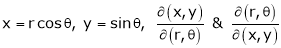
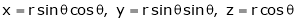
ST 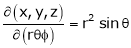
4.  find
find 
5. If 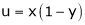 and
and 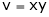 , find
, find 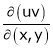
6. 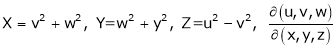
7. If 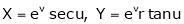
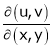
8. If 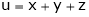 ,
, 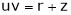 ,
, 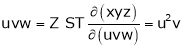
JJ1 = 1
If  ,
, 
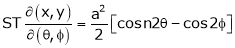
JJ1=1

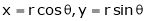
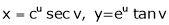
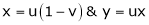
Jacobian of composite function (chain rule)
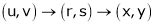
Then 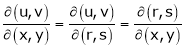
Ex.
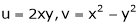
Where 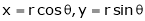
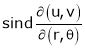
2. If 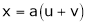
 and
and 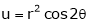

Find 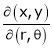
3. If 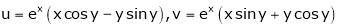
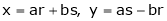
Find 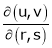
Jacobian of Implicit function
Let u1, u2 be implicit functions of x1, x2 connected by f1, f2 such there
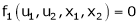 ,
, 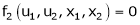
Then 
Similarly,
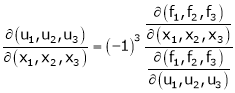
Ex.
If 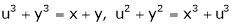
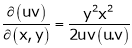
If 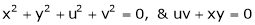
Find 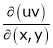
Taylor’s series
Let 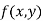 be a function of two variables x and y then
be a function of two variables x and y then
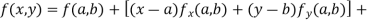
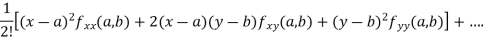
Which is known as Taylor’s expansion of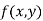 in power of
in power of 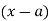 and
and  .
.
Malclaurian’s Series
It is particular case of Taylor’s theorem by putting a=0 and b=0
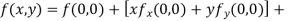
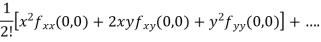
Example1:Expand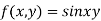 in power of
in power of 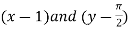 up to second terms.
up to second terms.
Given function 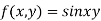
Here 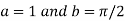
Now, 
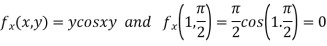
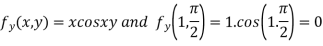

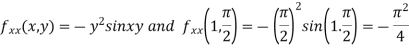
 and
and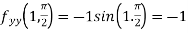
The Taylor’s expansion in power 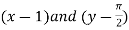 is
is

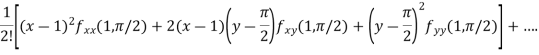
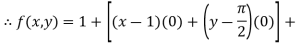
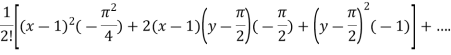
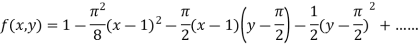
Example2: Expand the 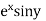 in power of x and y up to third term?
in power of x and y up to third term?
Given function 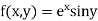
Now, 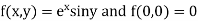
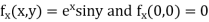
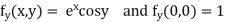
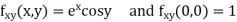
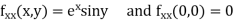
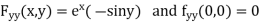
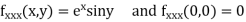

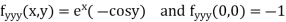
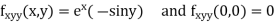
By Maclaurins expansion
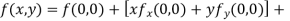
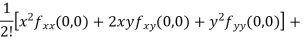
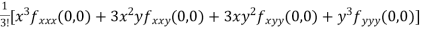 +…
+…

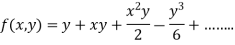
Let z = f(x, y)

Now for stationary point dz = 0
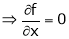 &
&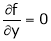
This gives the set of values of x and y for which maxima or minim occurs
Now find 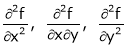
We called it as r, s, t resp.
Thus function has maximum or minimum
ifrt – s2>0
i.e. 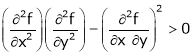
further if
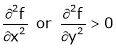
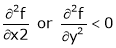
Note that
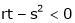
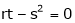
Ex. Discuss the stationary values of 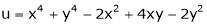
Ex. Find the values of x and y for which x2 + y2 + 6x = 12 has a minimum values and find its minimum value.
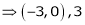
Divide 120 into three parts so that the sum of their product. Taken two at a times shall be maximum.
Using Lagrange’s method divide 24 into three parts. Such that continued product of the first, square of second, cube of third may be maximum.
Find the maximum and minimum value of x2 + y2 when 3x2 + 4xy + 6y2 = 140
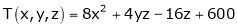
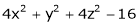 is satisfied.
is satisfied.
Let 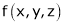 be a function of x, y, z which to be discussed for stationary value.
be a function of x, y, z which to be discussed for stationary value.
Let 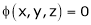 be a relation in x, y, z
be a relation in x, y, z
 for stationary values we have,
for stationary values we have,
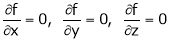
i.e. 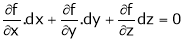 … (1)
… (1)
Also from 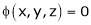 we have
we have
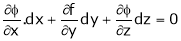 … (2)
… (2)
Let ‘ ’ be undetermined multiplier then multiplying equation (2) by
’ be undetermined multiplier then multiplying equation (2) by 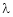 and adding in equation (1) we get,
and adding in equation (1) we get,
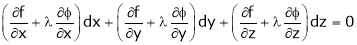
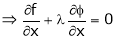 … (3)
… (3)
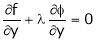 … (4)
… (4)
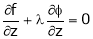 … (5)
… (5)
Solving equation (3), (4) (5) & we get values of x, y, z and 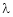 .
.
Solution:
Let x, y, z be the three parts of ‘a’ then we get.
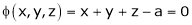 … (1)
… (1)
Here we have to maximize the product
i.e. 
 By Lagrange’s undetermined multiplier, we get,
By Lagrange’s undetermined multiplier, we get,
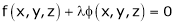
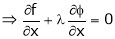 … (2)
… (2)
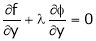 … (3)
… (3)
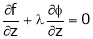 … (4)
… (4)
i.e.
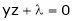 … (2)’
… (2)’
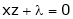 … (3)’
… (3)’
 … (4)
… (4)

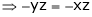

And 
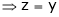
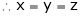
From (1)

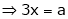
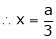
Thus 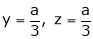 .
.
Hence their maximum product is 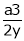 .
.
2. Find the point on plane  nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
Solution:
Let 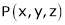 be the point on sphere
be the point on sphere 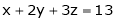 which is nearest to the point
which is nearest to the point 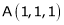 . Then shortest distance.
. Then shortest distance.
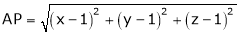
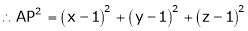
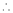 Let
Let 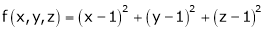
Under the condition 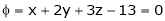 … (1)
… (1)
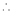 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have
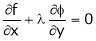
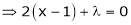 … (2)
… (2)
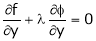
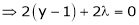 … (3)
… (3)
i.e.  &
&
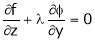
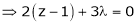 … (4)
… (4)
From (2) we get 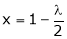
From (3) we get 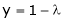
From (4) we get 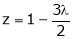
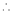 Equation (1) becomes
Equation (1) becomes
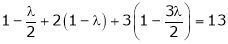
i.e. 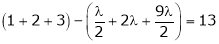
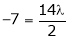
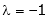
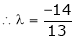
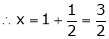
y = 2
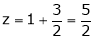
Exercise:
If 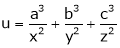 where x + y + z = 1.
where x + y + z = 1.
Prove that the stationary value of u is given by,
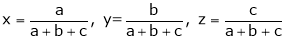
Reference Books:
1. A text book of Applied Mathematics Volume I and II by J.N. Wartikar and P.N. Wartikar
2. Higher Engineering Mathematics by Dr. B. S. Grewal
3. Advanced Engineering Mathematics by H. K. Dass
4. Advanced Engineering Mathematics by Erwins Kreyszig