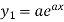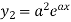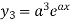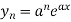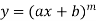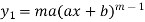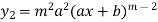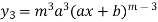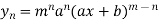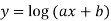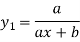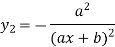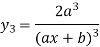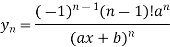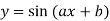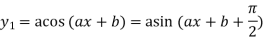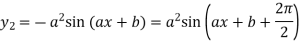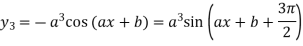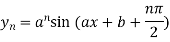UNIT 1
DIFFERENTIAL CALCULUS
It is the process of differentiating the given function simultaneously many times and the result obtained are called successive derivative.
Let  be a differentiable function.
be a differentiable function.
First derivative is denoted by 
Second derivative is 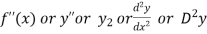
Third derivative is 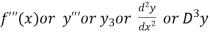
Similarly the nth derivative is 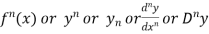
Example:
Function | Derivaties |
|
…………..
|
|
………..
|
|
…………
|
|
………….
|
Example1: Find the nth derivative of 
Since 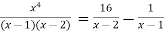
Differentiating both side with respect to x
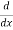 [
[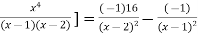
Again differentiating with respect to x
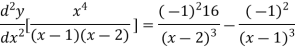
Again differentiating with respect to x
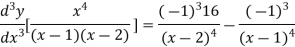
Similarly the nth derivative is
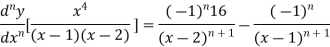
Example2: Find the nth derivative of 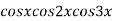
Let 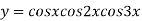
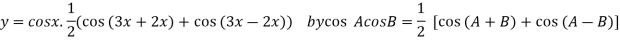
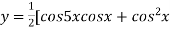 ]
]
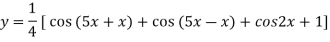
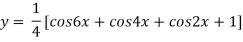
Differentiating with respect to x we get
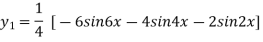

Again differentiating with respect to x we get

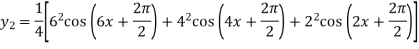
Again differentiating with respect to x we get
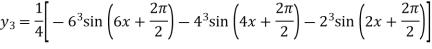
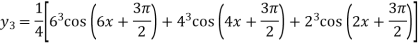
Similarly Again differentiating with respect to x we get
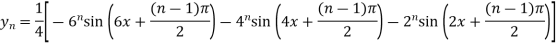
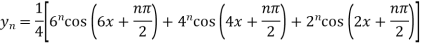
Example3: Find the nth derivative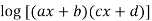
Let 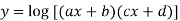
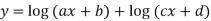
Differentiating with respect to x.
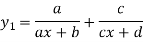
Again differentiating with respect to x.
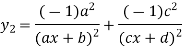
Again differentiating with respect to x.
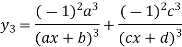
Again differentiating with respect to x.
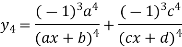
Again differentiating with respect to x.
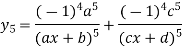
Similarly the nth derivative with respect to x.
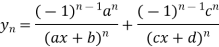
If u and v are the function of x such that their nth derivative exists, then the nth derivative of their product will be

Example1:Find the nth derivative of 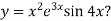
Let 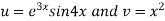
Also 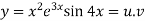
By Leibnitz’s theorem
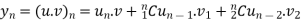
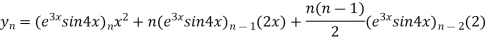
 …(i)
…(i)
Here 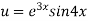
Differentiating with respect to x, we get
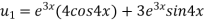
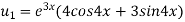
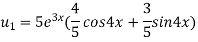
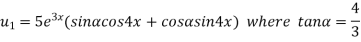

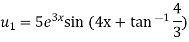
Again differentiating with respect to x, we get


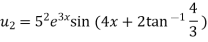
Similarly the nth derivative will be
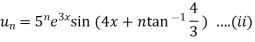
From (i) and (ii) we have,
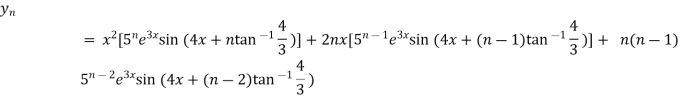
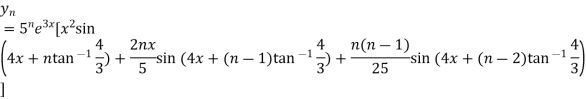
Example2: If 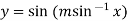 , then show that
, then show that
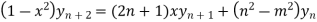
Also, find 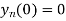
Here 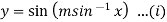
Differentiating with respect to x, we get
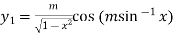 …(ii)
…(ii)

Squaring both side we get
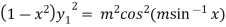
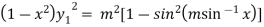
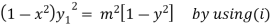
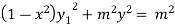 …(iii)
…(iii)
Again differentiating with respect to x ,we get
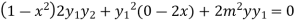
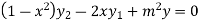
Using Leibnitz’s theorem we get
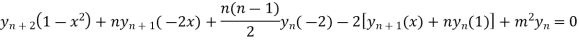
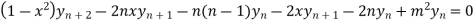
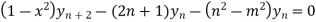 …(iv)
…(iv)
Putting x=0 in equation (i),(ii) and (iii) we get
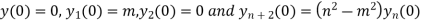
Putting n=1,2,3,4….
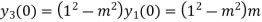
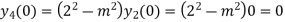
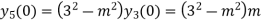
………………
Hence 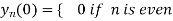
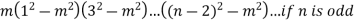
Example3: If 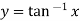 then show that
then show that
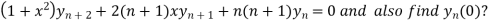
Given 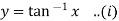
Differentiating both side with respect to x.
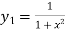 …..(ii)
…..(ii)
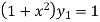
Again differentiating with respect to x, we get
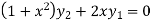 …(iii)
…(iii)
By Leibnitz’s theorem
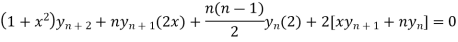
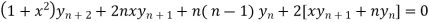
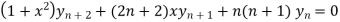
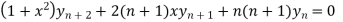 …(iv)
…(iv)
Putting x=0 in equation (i),(ii),(iii) and (iv) we get
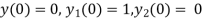
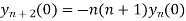
Putting n=1,2,3,4… so we get
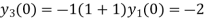
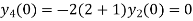
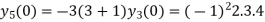
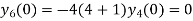
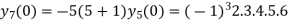
Hence we have
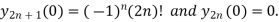
Taylor’s theorem:
If (i) f(x) and its first (n-1) derivative be continuous in [a, a+h],
(ii) 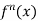 exist for every value of x in (a, a+h), then there is at least one number
exist for every value of x in (a, a+h), then there is at least one number 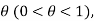 such that
such that
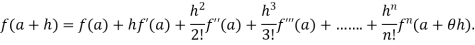
This is called Taylor’s theorem with Lagrange’s form of remainder
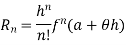
Taylor’s Series:
If 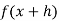 can be expanded as an infinite series, then
can be expanded as an infinite series, then
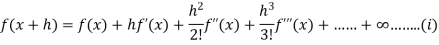
If 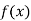 possesses derivative of all orders and the remainder
possesses derivative of all orders and the remainder  .
.
Corollary: Taking 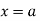 and
and 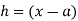 in equation (i) we get
in equation (i) we get

Taking 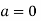 in above we get Maclaurin’s series.
in above we get Maclaurin’s series.
Example1: Expand the polynomial 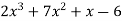 in power of
in power of 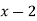 , by Taylor’s theorem.
, by Taylor’s theorem.
Let 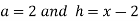 .
.
Also 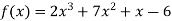
Then 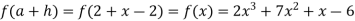
Differentiating with respect to x.
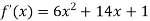
Again differentiating with respect to x the above function.
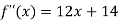
Again differentiating with respect to x the above function.
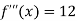
Also the value of above functions at x=2 will be
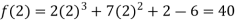
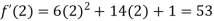
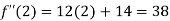

By Taylor’s theorem
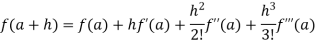
On substituting above values we get

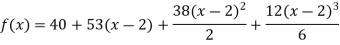

Example2: Expand 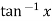 in power of
in power of 
Let 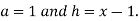
Also 
Differentiating f(x) with respect to x.

Again differentiating f(x) with respect to x.
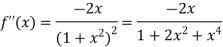
Again differentiating f(x) with respect to x.

Also the value of above functions at x=1 will be
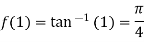

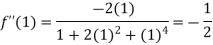
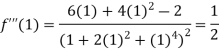
By Taylor’s theorem
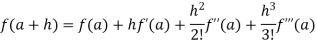
On substituting above values we get
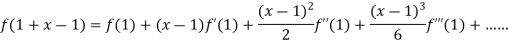
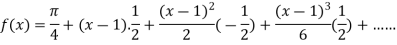
 =
= 
Example3:Expand 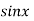 in power of
in power of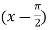 . Hence find the value of
. Hence find the value of 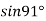 correct to four decimal places.
correct to four decimal places.
Let 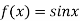
and 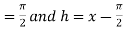 .
.
Differentiating 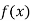 with respect to x.
with respect to x.

Again differentiating 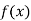 with respect to x.
with respect to x.
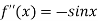
Again differentiating  with respect to x.
with respect to x.
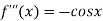
Again differentiating 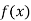 with respect to x.
with respect to x.
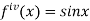
Also the value of above functions at  will be
will be
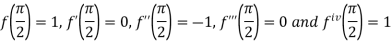
By Taylor’s theorem
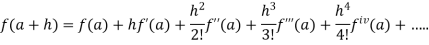
On substituting above values we get
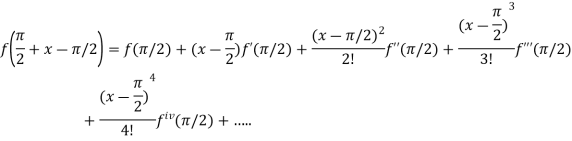
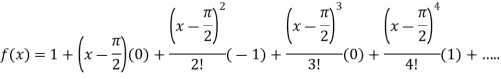
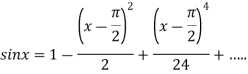
At 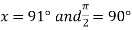
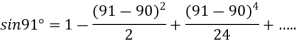

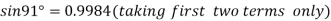 .
.
Maclaurin’s theorem:
This is a particular case of Taylor’s theorem in which a=0 and h=x in Taylor’s theorem.
If f(x) can be expanded as an infinite series, then
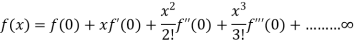
Where the remainder is 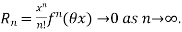
Example1:If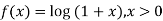 using Taylor’s theorem, show that for
using Taylor’s theorem, show that for 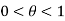 .
.
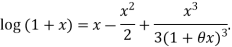
Deduce that 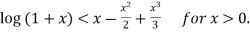
Let 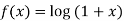 then
then 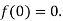
Differentiating with respect to x.
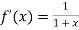 .Then
.Then 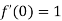
Again differentiating with respect to x.
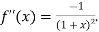 Then
Then 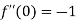
Again differentiating with respect to x.
 Then
Then 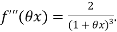
By Maclaurin’s theorem
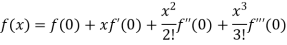
Substituting the above values we get
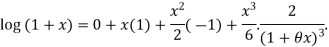
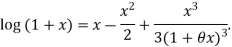
Since 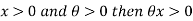
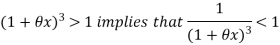
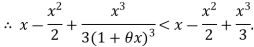
Hence 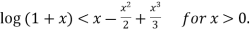
Example2: Prove that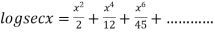
Let 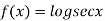
Differentiating 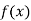 with respect to x.
with respect to x.
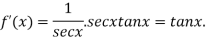
Again differentiating 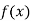 with respect to x.
with respect to x.
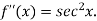
Again differentiating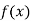 with respect to x.
with respect to x.
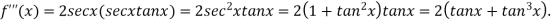
Again differentiating  with respect to x.
with respect to x.
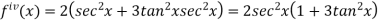 and so on.
and so on.
Putting  , in above derivatives we get
, in above derivatives we get
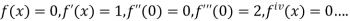 so on.
so on.
By Maclaurin’s theorem
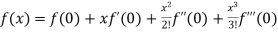 +………
+………
Substituting the above values we get
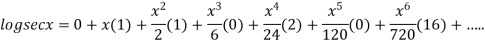
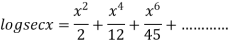
Example3:Prove that
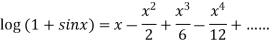
Let 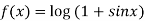
Differentiating above function with respect to x.

Again differentiating above function with respect to x.
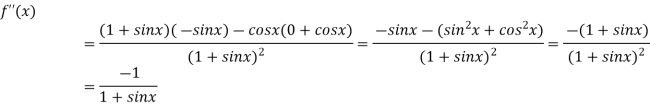
Again differentiating above function with respect to x.
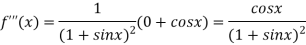
Again differentiating above function with respect to x.
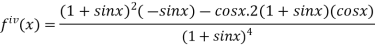
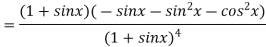

Putting 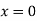 , in above derivatives we get
, in above derivatives we get
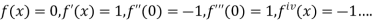 so on.
so on.
By Maclaurin’s theorem
 +………
+………
Substituting the above values we get
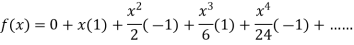
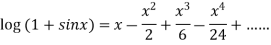
Example: Expansion of Some standard series
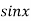
Let 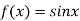 and
and 
Differentiating above function with respect to x.
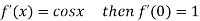
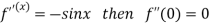
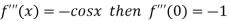


By Maclaurin’s theorem
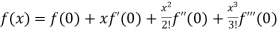 +………
+………
Substituting the above values we get
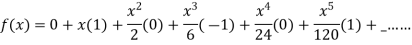
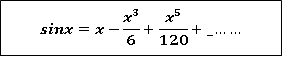
2. 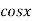
Let  and
and 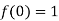
Differentiating above function with respect to x.
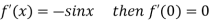
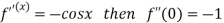
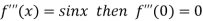
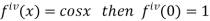

By Maclaurin’s theorem
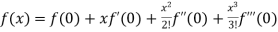 +………
+………
Substituting the above values we get
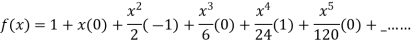
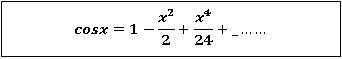
3.
Let 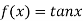 and
and 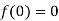
Differentiating above function with respect to x.
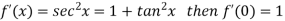 .
.
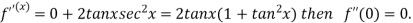


By Maclaurin’s theorem
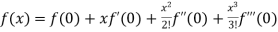 +………
+………
Substituting the above values we get
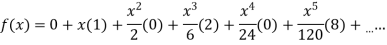
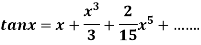
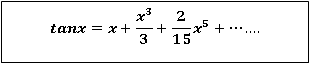
4.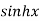
Let  and also
and also 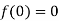
Differentiating above function with respect to x.
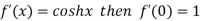
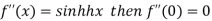
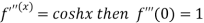
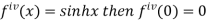

By Maclaurin’s theorem
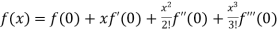 +………
+………
Substituting the above values we get
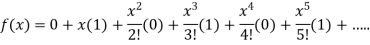
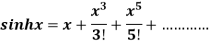
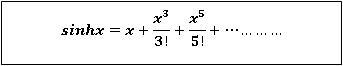
5. 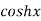
Let 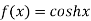 and also
and also 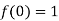
Differentiating above function with respect to x.
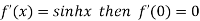

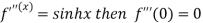
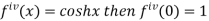
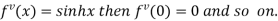
By Maclaurin’s theorem
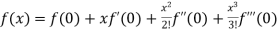 +………
+………
Substituting the above values we get
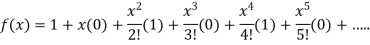
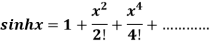
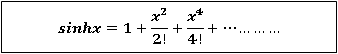
6. 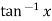
Let  and also
and also 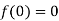
Differentiating above function with respect to x.
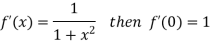
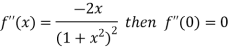
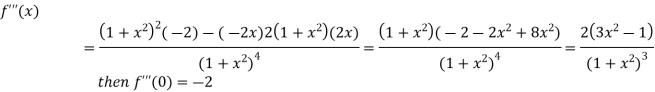
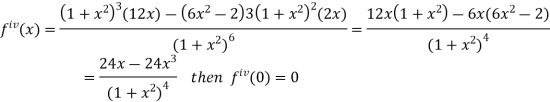
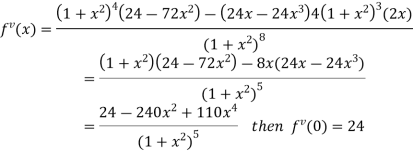
By Maclaurin’s theorem
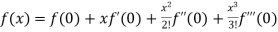 +………
+………
Substituting the above values we get
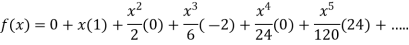

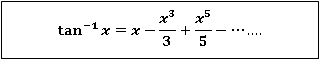
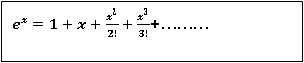
7. 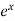
Let 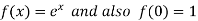
Differentiating above function with respect to x.
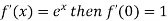
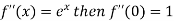
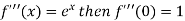
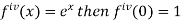
By Maclaurin’s theorem
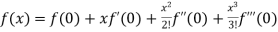 +………
+………
Substituting the above values we get
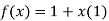 +
+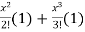 +………
+………
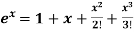 +………
+………
8. 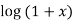
Let 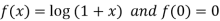
Differentiating above function with respect to x.
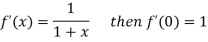
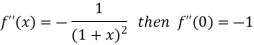
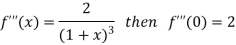
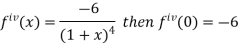
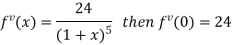
By Maclaurin’s theorem
 +………
+………
Substituting the above values we get
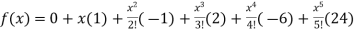 +………
+………
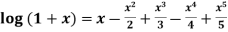 +………
+………
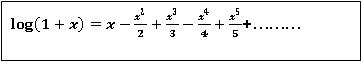
9. 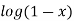
Let 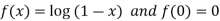
Differentiating above function with respect to x.
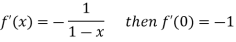

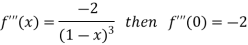
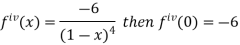
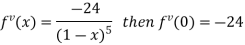
By Maclaurin’s theorem
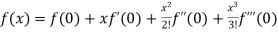 +………
+………
Substituting the above values we get
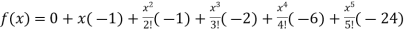 +………
+………
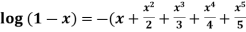 +………)
+………)
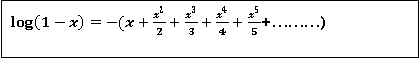
10. 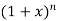
Let 
Differentiating the above function with respect to x.
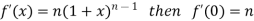
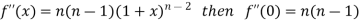
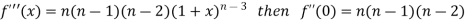
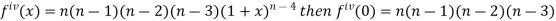
By Maclaurin’s theorem
 +………
+………
Substituting the above values we get

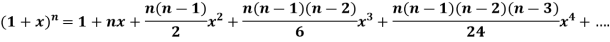
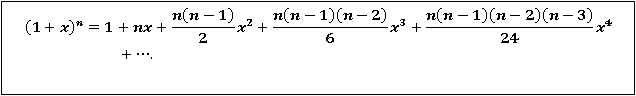
Let 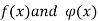 are functions of x only and have zero limit when
are functions of x only and have zero limit when 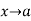 .(where a is a certain point)
.(where a is a certain point)
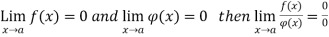 is called the indeterminate form. It means that
is called the indeterminate form. It means that  does not exist.
does not exist.
The indeterminate form is distributed in the following form:
1. Form 0/0:
If 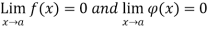 then
then

This is called L-Hospital Rule.
In case 
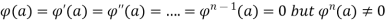
Then 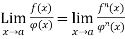
Differentiation of numerator and denominator are done separately as many times as required.
Example1: Evaluate the limits of 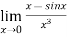
As we can see that 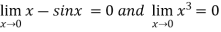
Therefore 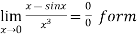
Using L-Hospital rule 
Again using L-Hospital Rule 
Again using L-Hospital Rule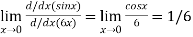
Hence 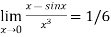
Example2:Evaluate the limits of 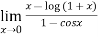
Since 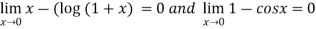
Therefore 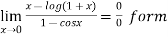
Using L-Hospital rule 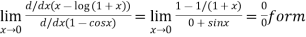
Again using L-Hospital Rule 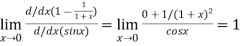
Hence 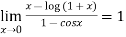
Example3:Evaluate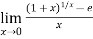
Since  form ….(i)
form ….(i)
Consider , let 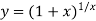
Taking log on both side
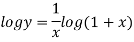
Differentiating both side with respect to x we get
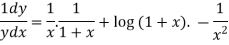
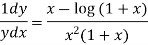
Or 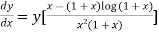
Or 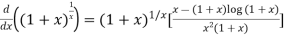 ….(ii)
….(ii)
Using L-Hospital Rule in (i) we have
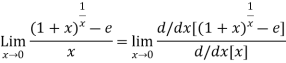
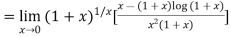 [using (ii)]
[using (ii)]
=0/0 form
Again Using L-Hospital Rule
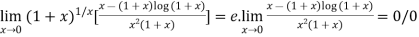 form
form
where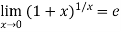
Again Using L-Hospital Rule
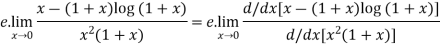
= 
= 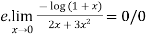 form
form
Again using L-Hospital rule
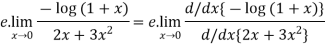
=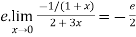
Hence 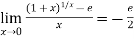 .
.
2. Form 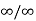 :
:
If  then
then
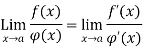
This is called L-Hospital Rule.
In case 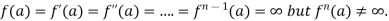
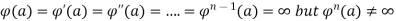 .
.
Then 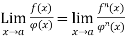
Differentiation of numerator and denominator are done separately as many times as required. We use series and standard limits.
Example1: Find 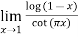
Since 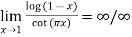 form
form
Using L-Hospital Rule 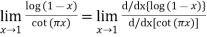
= 
= 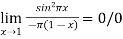 form
form
Again Using L-Hospital Rule
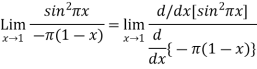
= 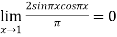
Hence 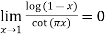
Example2: Find 
Since 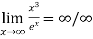 form
form
Using L-Hospital Rule
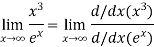
= 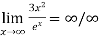 form
form
Again using L-Hospital Rule
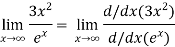
=  form
form
Again Using L-Hospital Rule
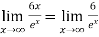 =
= 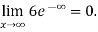
Hence 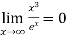 .
.
Example3: Evaluate the limit 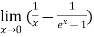
Since  form
form
Therefore 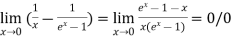 form
form
Using L-Hospital Rule
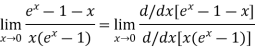
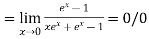 form
form
Again Using L-Hospital Rule
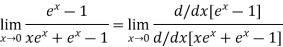
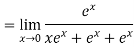
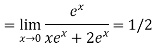
Hence 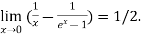
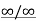
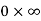
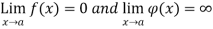
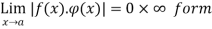
Then 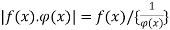 will be of the form 0/0 when
will be of the form 0/0 when 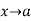 .
.
And 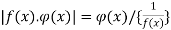 will be of the form
will be of the form 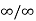 when
when 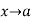
b. Form 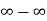 : If
: If 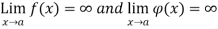 then
then

Then 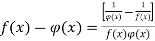
c. Forms 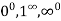 : If
: If 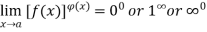 form.
form.
Let 
Taking log on both side we get
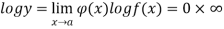
This is solved by the above method then we have 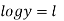 will give
will give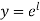 .
.
Example1: Evaluate the limit 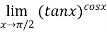
Since 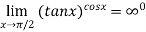 form
form
Let 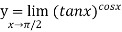
Taking log on both side we get
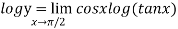
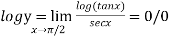 form
form
Using L-Hospital Rule
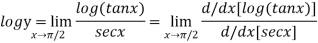
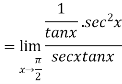
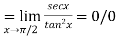 form
form
Again using L-Hospital Rule
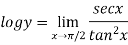
=
=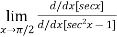
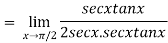
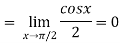
Here 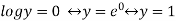
Hence 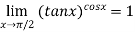 .
.
Example2: Evaluate the limit 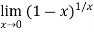
Since 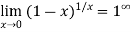 form
form
Let 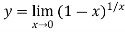
Taking log on both side we get
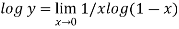
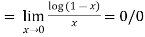 form
form
Using L-Hospital Rule we get


Here 
Hence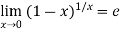 .
.
Example3:Evaluate the limit 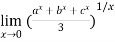
Since 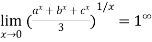
Let y = 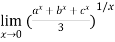
Taking log on both side we get
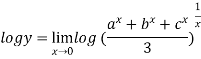
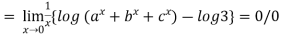 form
form
Using L-Hospital Rule we get
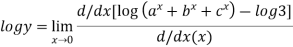
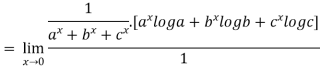
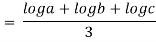
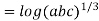
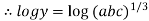
So, 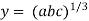
Hence 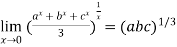
Reference Books:
1. A text book of Applied Mathematics Volume I and II by J.N. Wartikar and P.N. Wartikar
2. Higher Engineering Mathematics by Dr. B. S. Grewal
3. Advanced Engineering Mathematics by H. K. Dass
4. Advanced Engineering Mathematics by Erwins Kreyszig