UNIT-3
ELECTRON OPTICS, NUCLEAR PHYSICS
AND QUANTUM MECHANICS
J. J. Thomson first determined the specific charge (charge to mass ratio e/m) of the electron in 1887. . For his work J. J. Thomson received the Nobel Prize in Physics in 1906, “in recognition of the great merits of his theoretical and experimental investigations on the conduction of electricity by gases”.
The specific charge is defined as the charge per unit mass of the particle. Thomson discovered that the value of (e/m) was independent of the gas used and also independent of the nature of the electrodes. Thomson discovered that the value of (e/m) was independent of the gas used and also independent of the nature of the electrodes.
The importance of the mass-to-charge ratio is that two particles with the same mass-to-charge ratio move in the same path in a vacuum, when subjected to the same electric and magnetic fields.
PRINCIPLE
The fact that the cathode rays (electrons) are deflected by electric and magnetic fields is made use of in this method. When a narrow beam of charged particles are projected at constant speed (v) across a magnetic field in a direction perpendicular to the field, the beam of particles experiences a force, which makes them move in a circular path.
CONSTRUCTION
- It consists of a highly evacuated glass tube, fitted with electrodes.
- Electrons are produced by heating a tungsten filament electrically.
- Electrons are made to accelerate and form a beam by passing through discs A and B.
- They are passed through electric and magnetic field. Finally they fall on zinc sulphide screen
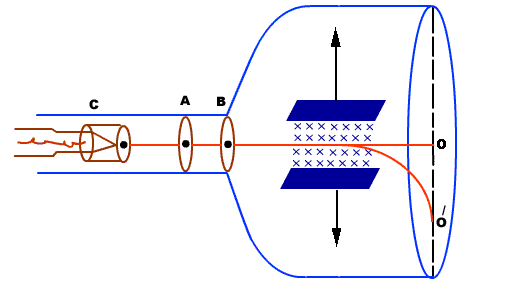Figure: Thomson’s method
.
THEORY
Actually electrons moving sideways are also directed towards the screen by applying a negative potential on a hollow cylinder (c) open on both sides surrounding the filament. Electrons are accelerated by applying a potential difference of above 1000 V between the filament and disc A. A further potential difference of 500 V is applied between the discs A and B. The arrangement focuses the beam to the hole of the disc B from where it is further proceeds to a straight line. When beam of electrons enters a magnetic field it moves in a circular track. The force experienced by the electron is
Fm = evB ……..(1)
This magnetic field provides necessary centripetal force to electron so that it follows a circular path. We know Fc =mv2/r. We have
So Fm = Fc
EvB =mv2/r
EB =mv/r
e/m =v/Br ……..(2)
By knowing the values of v, B and r, value of e/m can be determined.
RADIUS OF CURVATURE OF PATH
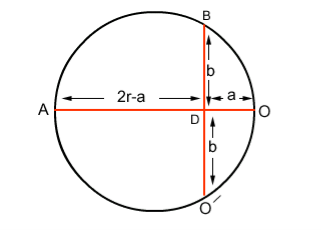
If r is the radius of curvature of circular path, ‘a’ is the distance b/w ‘O’ and ‘O/’, and ‘b’ is the distance b/w electron gun and screen then by using the property of chord:
AD x OD = BD x DO
(2r-a) x a =b.b
(2ra-a2) = b2
Since 2r is very small as comapred to a2
2ra = b2
r = b2/2a ……..(3)
DETERMINE VELOCITY BY FIRST METHOD
The electrons are first accelerated by applying a potential (V) b/w discs A and B before entering the magnetic field.
K.E =Ve
1/2mv2 =Ve
v= (2Ve/m)1/2
We know from eq (2) e/m =v/Br put value of v in eq (2) we get
e/m = {(2Ve/m)1/2}/Br
Squaring on both sides, we have
e2/m2 = (2Ve/m)/B2r2
e/m = 2V/B2r2 ……..(4)
PARTICLE SELECTOR METHOD
This is a more accurate method as compared to the above method. In this method, the beam is passed through crossed electric and magnetic field. The electric field is so adjusted that the light spot comes back to ‘O’ from ‘O/’. i.e. electron beam passes and straight without deflection.
Force on electron by electric field
Fe=Ee
Force on electron by magnetic field
Fm= Bev
Since, both forces balance each other
Fm = Fe
Bev = Ee
v = E/B ……..(5)
We know e/m =v/Br by eq (2), substituting v from above equation (5) we have
e/m = (E/B)/Br
e/m = E/B2r ……..(6)
By knowing E, B and r we are able to find e/m ratio.
Thus In his experiment, J. J. Thomson had found a charged particle that had a specific charge two thousand times that of the hydrogen ion, the lightest particle known at that time. Once the charge on the particles was measured he could conclude with certainty that these particles were two thousand times lighter than hydrogen. This explained how these particles could pass between atoms and make their way out of thin sheets of gold. Measurement of the specific charge of cathode rays for different metals made him conclude that the particles that constituted cathode rays form a part of all the atoms in the universe. The direct measurement of mass of the electron is difficult by experiments. It is easier to determine the specific charge of the electron e/m from which the mass m can be calculated if the elementary charge e is known.
The oil drop experiment was performed by Robert A. Millikan and Harvey Fletcher in 1909 to measure the charge of the electron.
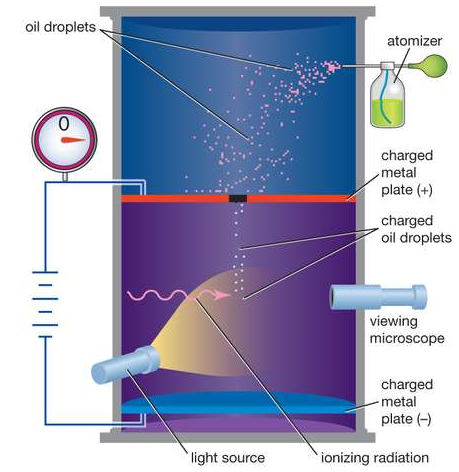
Figure: Millikan’s Oil Drop Experiment
PRINCIPLE
This method is based on the study of the motion of uncharged oil drop under free fall due to gravity and charged oil drop in a uniform electric field. By adjusting uniform electric field suitably, a charged oil drop can be made to move up or down or even kept balanced in the field of view for sufficiently long time and a series of observations can be made.
They suspended tiny charged droplets of oil between two metal electrodes by balancing downward gravitational force with upward drag and electric forces.
The density of the oil was known, so Millikan and Fletcher could determine the droplets’ masses from their observed radii .Since from the radii they could calculate the volume and thus, the mass.
Using the known electric field and the values of gravity and mass, Millikan and Fletcher determined the charge on oil droplets in mechanical equilibrium.
CONSTRUCTION
- The apparatus consists of two horizontal circular metal plates A and B.
- By applying a potential difference across the plates, a uniform electric field was created in the space between them.
- These plates are held together by insulating rods of glass or ebonite, so that they are perfectly parallel to each other.
- The plates are surrounded by a constant temperature bath D and the chamber C containing dry air.
- The plates are connected to a battery which can provide a potential difference.
- Four holes were cut into the ring, three for illumination by a bright light, and another to allow viewing through a microscope.
THEORY
The apparatus incorporated a pair of metal plates and a specific type of oil. Millikan and Fletcher discovered it was best to use an oil with an extremely low vapour pressure, such as one designed for use in a vacuum apparatus. Ordinary oil would evaporate under the heat of the light source, causing the mass of the oil drop to change over the course of the experiment.
Some oil drops became electrically charged through friction with the nozzle as they were sprayed.
The droplets entered the space between the plates and, because they were charged, they could be controlled by changing the voltage across the plates. Initially, the oil drops were allowed to fall between the plates with the electric field turned off.
As they attained terminal velocity due to friction with the air in the chamber. The field was turned on and, if it was large enough, some of the drops (the charged ones) would start to rise. This is because the upwards electric force, FE, is greater for them than the downwards gravitational force,
One such droplet is viewed through the microscope as it descends under gravity the selected drop was kept in the middle of the field of view by alternately switching off the voltage until all the other drops fell. The experiment was continued with this single drop.
Millikan’s experiment was meant to have the drops fall at a constant rate. At this constant rate, the force of gravity on the drop and the force of the electric field on the drop are equal:
MATHEMATICALLY
(i) Motion under gravity
The gravitational force acting on the oil drop downwards is equal to mg =4/3 πa3 ρ g,
Where a is the radius of the oil drop, ρ is the density of the oil and g, the acceleration due to gravity.
The upthrust experienced by the oil drop due to the displaced air is 4/3 πa3 σ g, where σ is the density of air.
∴ The net downward force acting on the oil drop = weight of the oil drop - upthrust experienced by the oil drop.
= ( 4/3 πa3 ρ g ) - ( 4/3 πa3 σ g )
= 4/3 πa3 (ρ - σ) g
Since the oil drop attains a terminal velocity v, the net downward force acting on the oil drop is equal to the viscous force acting opposite to the direction of motion of the oil drop.
By Stoke's law, the viscous force on the oil drop is 6πaηv, where η is the co-efficient of viscosity of air.
4 / 3 πa3 (ρ - σ) g = 6πaηv ……(2)
The radius of the oil drop is,
A= [9ηv / 2(ρ - σ)g ]1/2
(ii) Motion under electric field
The air inside the parallel plates is ionized by sending a beam of X-rays. The droplets pickup one or more electrons from the ionized air.
Let q be the charge carried by the droplet under observation. Let E be the electric field applied between the plates A and B, so that the drop moves upwards with a terminal velocity v1, which can be determined using the microscope.
The force on the droplet due to electric field is Eq. Since the velocity of the droplet is uniform, we have
Eq = 4/3 πa3 ( ρ - σ ) g + 6π aηv1
Eq - 4/3 πa3 ( ρ - σ ) g = 6π aηv1 (4)
Adding equations (2) and (4),
Eq = 6πaη(v + v1) (5)
Substituting the value of a in equation (5) from equation (3),
Eq = 6πη3/2(v + v1 ) [9v/2( ρ - σ ) g]1/2 …..(6)
If V is the potential difference between A and B, d is the distance between them, then E =V/d
Millikan determined the value q for a large number of oil drops using equation (6) and found that they are an integral multiple of a least value. The greatest common factor gives the charge e of the electron.
The charge of an electron was found to be 1.602 x10-19 coulomb.
Bainbridge mass spectrometer is an instrument used for the accurate determination of atomic masses.
PRINCIPLE
Uniform magnetic field acting normal to the path of ions having same velocity deflects the ions of different masses from a straight path to circular path of different radii.
CONSTRUCTION
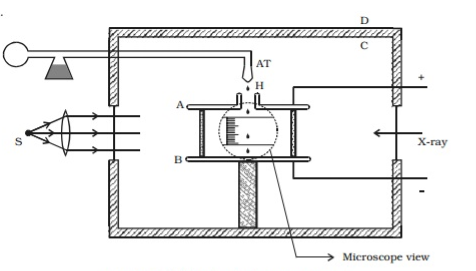
(i) Ionization Chamber
Ionization chamber is used to ionize the gas whose mass or isotope is to be determined and positive ions are produced.
(ii) Velocity Selector
Velocity selector has two fields electric and magnetic field both are applied perpendicular to the moving ion beam. A potential (V) is applied between two electrodes to produce the electric field. A magnetic field (strength B) is applied at right angles to the electrostatic field and so the electrostatic and electromagnetic forces act in opposite directions to each other. A velocity selector is used to produce a monovelocity ion beam and a transverse magnetic field is employed to discriminate between ions of different masses.
(iii) Vacuum / Analyzing Chamber
Vacuum / Analyzing Chamber is a semi-spherical cavity in which another magnetic field B’ is applied perpendicular to the moving positive ion.
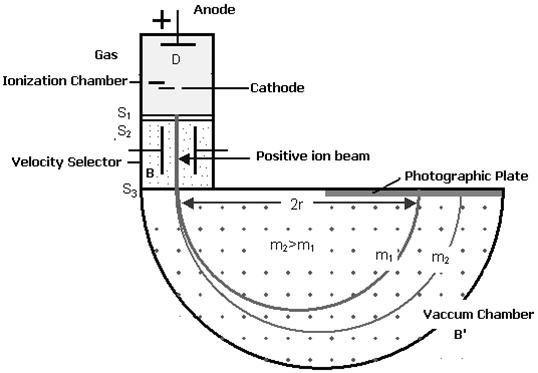
Figure: Bainbridge Mass Spectrograph
WORKING
Atoms with one or more electrons removed, have a net positive charge and they become positive ions. A beam of positive ions produced in a discharge tube is collimated into a fine beam by two narrow slits S1and S2 . This fine beam enters into a velocity selector.
The velocity selector allows the ions of a p articular velocity to come out of it, by the combined action of an electric and a magnetic field. The velocity selector consists of two plane parallel plates P1 and P2, which produces a uniform electric field E and an electromagnet, to produce uniform magnetic field B (represented by the dotted circle). These two fields are at right angles to each other and to the direction of the beam.
The electric field and magnetic field are so adjusted that the deflection produced by one field is nullified by the other, so that the ions do not suffer any deflection within the velocity selector.
Ions are formed in ionization chamber and pass through the cathode, then through collimating slits S1 and S2. The beam is then passed through velocity selector in which electric and magnetic fields are applied perpendicular to each other. The ion moves in straight line path for which both the forces acting on it are equal
Let E and B be the electric field intensity and magnetic induction respectively and q be the charge of the positive ion. The force exerted by the electric field is equal to qE and the force exerted by the magnetic field is equal to qvB where v is the velocity of the positive ion.
QE =qvB
The velocity of ion which passes undeflected through the velocity selector is
v = E/B
In the vacuum chamber the ions are affected by the magnetic field (B’) alone and so move in circular paths, the lighter ions having the larger path radius. If the mass of an ion is M, its charge q and its velocity v then
QvB’ =Mv2 /R
R =Mv/qB’
So radius of path is directly proportional to mass of the ion i.e. R ∝ M
Further substitute the value of v
R =ME/qBB’ or M =RqBB’/E
Ions with different masses trace semi-circular paths of different radii and produce dark lines on the plate. The distance between the opening of the chamber and the position of the dark line gives the diameter 2R from which radius R can be calculated.
Since, B,B′,E and R are known, the mass of the positive ions and hence isotopic masses can be calculated.
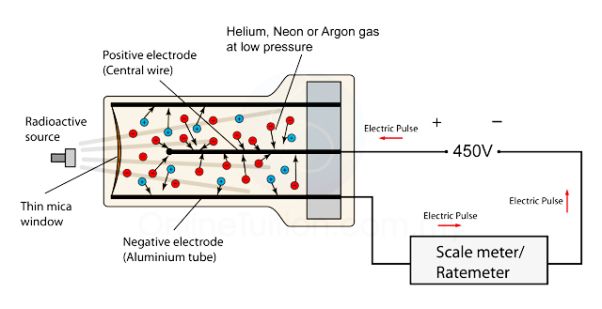
A ‘particle detector’ to measure the ionizing radiation was developed by Geiger and Muller in the year 1928 and they called it a ‘Geiger Muller Counter’ which in short is known as the ‘GM counter.’
The G.M. Counter is a radiation detector. As Nuclear radiations emitted by disintegrating nuclei cannot be sensed directly. Indirect methods are employed to detect them.
PRINCIPLE
The ionizing particle passing through the tube ionizes the gas and electrons so produced move towards Anode. The velocity is quite high and they later produce secondary electrons after repeated collisions with the particles of the gas. These secondary electrons further produce more electrons in Geometric progression.
Due to this large multiplication action, a large ionization current is produced.
CONSTRUCTION
- The G. M. Tube consists of a rugged metal cylinder which acts as cathode.
- A wire of tungsten runs through the axis of the tube, it acts as anode.
- Cathode and anode are separated by ebonite plugs.
- Both the cathode and anode are connected with high DC battery (1000 – 2000 Volts).
- Heavy load is connected in series.
- At one end a thin window of mica is arranged to allow the entry of radiation in the tube.
- The tube is evacuated then is filled with 90% Argon at 10 cm pressure and 10% ethyl alcohol vapours at 1 cm pressure.
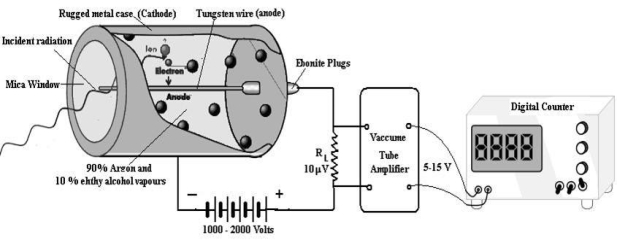
A dc potential about 1200 volt is applied between the cathode and anode. When the radiation enters in the GM tube through the mica window it ionizes few argon atoms. If the applied voltage is strong enough, these ion produce a secondary avalanche that causes a current pulse. The current through RL produces a voltage pulse. This voltage is amplified up to 5 -15 Volt by vacuum tube amplifiers and is then applied to the counter. As each incoming radiation produces a pulse the number of radiation are counted. A rate meter or digital counter indicates the number of pulses or counts per second. The complete apparatus is often called a Geiger counter.
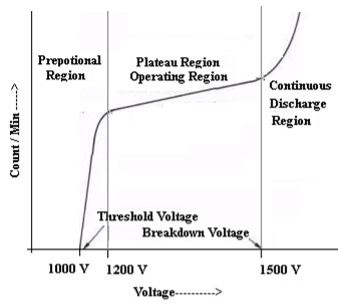
CHARACTERISTIC OF G M COUNTER
The characteristic shows the plot of count / min as a function of voltage
- For voltage less than 1000 Volt there is no discharge and hence no counts.
- Between 1000 – 1200 Volts, the number of count increases linearly with the applied voltage. The region is called proportional region
- Above 1200 Volt upto 1500 Volt the count rate shows least variation, almost constant the region is called the plateau region or Geiger region or Operating region.
- If the voltage is applied above 1500 volt a continuous discharge will take place, count rate increases rapidly due to discharge of Argon gas which is undesirable.
QUENCHING
It is the process to prevent the continuous discharge. Self-quenching is done by vapours of ethyl alcohol because its ionization energy is less than the ionization energy of Argon atom.
COUNTING RATE
The G M Counter can count about 5000 particles / sec. The counting rate depends upon the death and recovery time of G M Counter.
DEATH TIME
In the counter, the slowly moving positive argon ion takes 200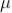 
sec to reach the cathode. If the second radiation enters the tube during this time, it will not be registered this time is called death time of the counter
RECOVERY TIME
After death time the tube takes another 200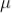 
sec to regain the original working condition. This time is called recovery time of the counter.
PARALYSIS TIME
The sum of death and recovery time is known as paralysis time, which is 400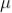 
sec. The tube can respond to the second radiation after 400 
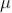sec
TRUE COUNT RATE
If the death time of the counter is τ and the count which is measured by the counter is no then, the true count rate n,
n = n0 / 1-no τ
ADVANTAGES OF GM COUNTER
- It can count alpha, beta, gamma particles as well as cosmic rays.
- It has high sensitivity.
- Power supply need not be precisely regulated as the pulse height is constant over a large range.
- Because of the fact that output pulse is very high, so the Amplification needed is also very subtle.
DISADVANTAGES OF GM COUNTER
- Energies cannot be measured by it as it has a lack of differentiating abilities.
- It cannot detect uncharged particles like Neutrons.
- It is less efficient due to the large paralysis time limits and large dead time.
- Quenching agent used in this counter often decomposes, leading to less lifetime of the GM Counter.
Thus, GM Counter is the one which is primarily used due to its advantages. Although it is not free from disadvantages, still its uses make it preferable over other counters.
USE
- It is used to detect and measure particles in the ionized gases.
- It is widely used in applications like radiological protection, radiation dosimetry and experimental physics
When radioactive isotopes are used in medical research work on humans, it is important to make sure that the amount of radioactive material administered to human subjects is as little as possible. In order to achieve this, a very sensitive instrument is necessary to measure the radioactivity of materials.
According to classical physics, given the initial conditions and the forces acting on a system, the future behaviour (unique path) of this physical system can be determined exactly. That is, if the initial coordinates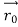
, velocity 
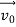, and all the forces acting on the particle are known, the position 
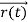, and velocity 
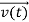are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.
Does this hold for the microphysical world?
Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle.
In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
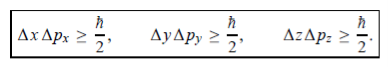
This principle indicates that, although it is possible to measure the momentum or position of a particle accurately, it is not possible to measure these two observables simultaneously to an arbitrary accuracy. That is, we cannot localize a microscopic particle without giving to it a rather large momentum.
We cannot measure the position without disturbing it; there is no way to carry out such a measurement passively as it is bound to change the momentum.
To understand this, consider measuring the position of a macroscopic object (you can consider a car) and the position of a microscopic system (you can consider an electron in an atom). On the one hand, to locate the position of a macroscopic object, you need simply to observe it; the light that strikes it and gets reflected to the detector (your eyes or a measuring device) can in no measurable way affect the motion of the object.
On the other hand, to measure the position of an electron in an atom, you must use radiation of very short wavelength (the size of the atom). The energy of this radiation is high enough to change tremendously the momentum of the electron; the mere observation of the electron affects its motion so much that it can knock it entirely out of its orbit.
It is therefore impossible to determine the position and the momentum simultaneously to arbitrary accuracy. If a particle were localized, its wave function would become zero everywhere else and its wave would then have a very short wavelength. According to de Broglie’s relation p = ℏ /λ,
TIME ENERGY UNCERTAINTY RELATION
The momentum of this particle will be rather high. Formally, this means that if a particle is accurately localized (i.e., ∆x 
0), there will be total uncertainty about its momentum (i.e., ∆px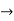 
∞).
Since all quantum phenomena are described by waves, we have no choice but to accept limits on our ability to measure simultaneously any two complementary variables.
Heisenberg’s uncertainty principle can be generalized to any pair of complementary, or canonically conjugate, dynamical variables: it is impossible to devise an experiment that can measure simultaneously two complementary variables to arbitrary accuracy .If this were ever achieved, the theory of quantum mechanics would collapse.
Energy and time, for instance, form a pair of complementary variables. Their simultaneous measurement must obey the time–energy uncertainty relation:
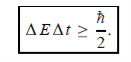
This relation states that if we make two measurements of the energy of a system and if these measurements are separated by a time interval ∆t, the measured energies will differ by an amount ∆E which can in no way be smaller than ℏ /∆t. If the time interval between the two measurements is large, the energy difference will be small. This can be attributed to the fact that, when the first measurement is carried out, the system becomes perturbed and it takes it a long time to return to its initial, unperturbed state. This expression is particularly useful in the study of decay processes, for it specifies the relationship between the mean lifetime and the energy width of the excited states.
In contrast to classical physics, quantum mechanics is a completely indeterministic theory. Asking about the position or momentum of an electron, one cannot get a definite answer; only a probabilistic answer is possible.
According to the uncertainty principle, if the position of a quantum system is well defined its momentum will be totally undefined.
1 Example: The uncertainty in the momentum of a ball travelling at 20m/s is 1×10−6 of its momentum. Calculate the uncertainty in position? Mass of the ball is given as 0.5kg.
Solution:
Given
v = 20m/s,
m = 0.5kg,
h = 6.626 × 10-34 m2 kg / s
Δp =p×1×10−6
As we know that,
P = m×v = 0.5×20 = 10kgm/s
Δp = 10×1×10−6
Δp = 10-5
Heisenberg Uncertainty principle formula is given as,
∆x∆p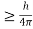 
∆x 
∆x 
∆x =0.527 x 10-29 m
2 Example: .The mass of a ball is 0.15 kg & its uncertainty in position to 10–10m. What is the value of uncertainty in its velocity?
Solution:
Given
m=0.15 kg.
h=6.6×10-34 Joule-Sec.
Δx = 10 –10 m
Δv=?
Δx.Δv ≥h/4πm
Δv≥h/4πmΔx
≥6.6×10-34/4×3.14×0.15×10–10
≥ 3.50×10–24m
APPLICATIONS OF HEISENBERG UNCERTAINTY PRINCIPLE
The Heisenberg uncertainty principle based on quantum physics explains a number of facts which could not be explained by classical physics.
- NON-EXISTENCE OF ELECTRONS IN THE NUCLEUS
One of the applications is to prove that electron cannot exist inside the nucleus.
But to prove it, let us assume that electrons exist in the nucleus.
As the radius of the nucleus in approximately 10-14m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by
According to uncertainty principle
∆x ∆p =h/2π
Thus ∆p=h/2π∆x
Or ∆p=6.62 x10-34/2 x 3.14 x 10-14
Or ∆p=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron then the momentum of electron should be at least of this order that is p=1.05*10-20 kg m/sec.
An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formula
E =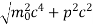 
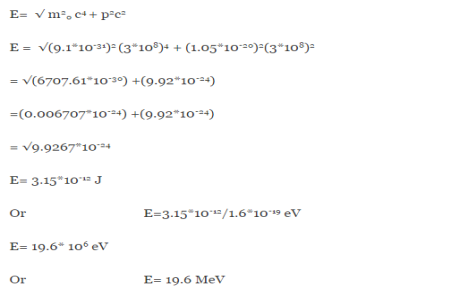
Therefore, if the electron exists in the nucleus, it should have an energy of the order of 19.6 MeV.
However, it is observed that beta-particles (electrons) ejected from the nucleus during b – decay have energies of approximately 3 Me V, which is quite different from the calculated value of 19.6 MeV.
Another reason that electron cannot exist inside the nucleus is that experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.
Therefore, it is confirmed that electrons do not exist inside the nucleus.
2. CALCULATION OF ZERO POINT ENERGY
The minimum energy of a system at o k (zero kelvin) is called zero point energy.
Consider a particle which is confined to move under the influence of potential of dimensions a. Since the particle may be present anywhere in these dimensions, so uncertainty in position
∆x = a/2 (half the diameter).
According to uncertainty principle
∆x∆px = ℏ/2
Or
Thus ∆px= ℏ /2∆x
∆px= ℏ /2a/2 = ℏ /a
Uncertainty in momentum of particle along x-axis is
∆px= ℏ /a
Assuming the momentum of particle to be at least equal to uncertainty in it, the lowest possible value of K.E. Of particle is given by
K.E. =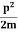 
= 
=
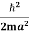
Where m is the mass of the particle.
Energy even at O K is given by the above equation. This minimum energy is called the zero-point energy.
This implies that even at zero kelvin, the particle is never at rest. If it is so, then ∆pX = 0, which is not possible. [It gives ∆x = ∞]
3. EXISTENCE OF PROTON, NEUTRON AND ALPHA PARTICLES WITHIN THE NUCLEUS.
We know that the rest mass of the protons and neutron is of the order of
1.67x 10-27 kg. Hence, the value of momentum 5.27 x 10-21 kg.m/sec from calculation and also the value of v come out to be 3x 105m/sec.
The corresponding value of kinetic energy of a neutron or a proton is
E =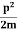 
= 
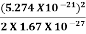=8.33 x 10-15J =
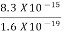eV
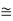52.05 keV
Since the rest mass of the a-particle is nearly four times the proton mass, therefore the alpha particle should have a minimum kinetic energy of one fourth of 52.05 keV, or about 13 keV. Since the energy carried by the protons or neutrons emitted by the nuclei are greater than 52 keV and for a-particle more than 13 keV, these particles can exist in the nuclei.
4. SIZE OF ELEMENTARY CELL IN PHASE SPACE
We have studied in our previous class that state of a microsystem is defined by six variables – three are due to position and three due to momentum.
Hence, a system of N particles needs 6 N variables
If ∆ x and ∆px be the uncertainly in position and in momentum measurements then
∆ x ∆ px = 
;
Similarly ∆ y ∆ py = 
,
And ∆ z ∆ pz = 
,
Multiplying these three equations, we get
∆ x ∆ y ∆ z ∆ px ∆ py ∆ pz = ( 
)3 in the units (J3 S3).
The above product is called the volume of elementary cell in phase space.
So, volume of an elementary cell in phase space 
10-101 units, (for quantum statistics) being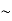 
.
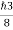5. ACCURATE LIMIT OF FREQUENCY OF RADIATION EMITTED BY AN ATOM
Consider the radiation emitted from an excited atom. The energy of this atom will decrease when it emits one or more photons of characteristic frequency.
The average period between excitation of the atom and the release of energy is about 10-8 seconds.
Thus, uncertainly in energy is
∆ E 
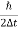
Or ∆ E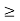 
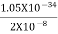J
Or ∆ E 
5.3 x 10-27 J
Frequency of light is uncertain by
∆ ν =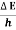 
= 
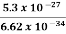Hz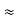 
0.8 x 107 Hz
As a result, the radiation from an excited atom does not have the noted precise frequency new ν - ∆ ν and ν + ∆ ν.
WAVE EQUATIONS
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So We have
E= K+V =
mv2+V(x) =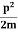
+V(x) ……….. (1)
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk.
Using this equation (1) for the energy will become
ℏω =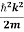 
+ V(x) ……….. (2)
A wave with frequency ω and wave number k can be written as usual as
ψ(x, t) =Aei(kx−ωt) ……….. (3)
The above equation is for one dimensional and for three dimensional we can write it as
ψ(r, t) =Aei(k·r−ωt) ……….. (4)
But here we will stick to one dimension only.
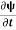=−iωψ ⇒ ωψ=
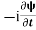……….. (5)
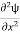=−k2ψ ⇒ k2ψ = - 
……….. (6)
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain
ℏ(ωψ) =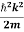 
ψ+ V(x) ψ ⇒ 
= - 
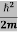
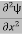+ V(x) ψ ……….. (7)
This is the time-dependent Schrodinger equation.
If we put the x and t in above equation then equation (7) takes the form as given below
= - 
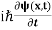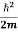
+ V(x) ψ(x,t) ……….. (8)
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the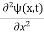 
term becomes ∇2ψ.
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
= - 
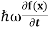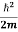
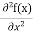+ V(x) f(x) ……….. (9)
We already know that E=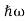
. However ψ(x, t) is general convention to also use the letter ψ to denote the spatial part. So we will now replace f(x) with ψ(x)
Eψ = - 
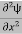+ V(x) ψ ……….. (10)
This is called the time-independent Schrodinger equation.
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as
ψ(x, y, z, t) = a + ib
And its complex conjugate as
ψ*(x, y, z, t) = a – ib.
The product of wave function and its complex conjugate is
ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2
a2 + b2 is a real quantity.
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
- The wave function must be single valued at each point.
- The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.
- ψ must be finite everywhere.
- ψ must be continuous everywhere and
must also be continuous everywhere except where V(x) is infinite. - ψ (x) must vanish ψ
0 as x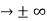
. - The wave function should satisfy the normalization condition. Normalization condition of a wave function ψ is mathematical statement of existence of the particle somewhere. so that if we sum up all possible values ∑|ψ(xi,t)|2∆xi we must obtain 1. The total probability of finding the particle anywhere must be one. Normalization condition is given as
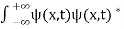dx =1
Only wave function with all these properties can yield physically meaningful result.
PHYSICAL SIGNIFICANCE OF WAVE FUNCTION
- The wave function ‘Ѱ’ has no physical meaning. It is a complex quantity representing the variation of a matter wave.
- The wave function Ѱ(r,t) describes the position of particle with respect to time .
- It can be considered as ‘probability amplitude’ since it is used to find the location of the particle.
- The square of the wave function gives the probability density of the particle which is represented by the wave function itself.
- More the value of probability density, more likely to find the particle in that region.
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.
All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics.
