Unit – 2
Partial Differentiation
Let f(x , y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as 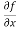 and defined as follows:
and defined as follows:
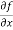 =
= 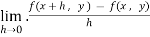
Now the partial derivative of f with respect to f can be written as  and defined as follows:
and defined as follows:
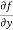 =
= 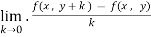
Note: a. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating , as constant.
b. We apply all differentiation rules.
Let f(x , y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives.
These are second order four partial derivatives:
(a) 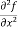 =
= 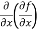
(b) 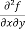 =
= 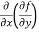
(c) 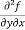 =
= 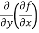
(d) 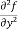 =
= 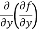
b and c are known as mixed partial derivatives.
Similarly we can find the other higher order derivatives.
Now we will understand the partial derivative by some examples:
Example1- Calculate 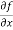 and
and 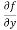 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Solution: To calculate 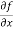 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
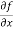 =
= 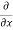 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 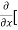 3x³] -
3x³] - 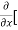 5y²] +
5y²] + 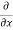 [2xy] -
[2xy] -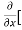 8x] +
8x] +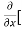 4y] -
4y] - 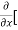 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
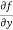 =
= 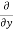 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 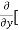 3x³] -
3x³] - 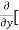 5y²] +
5y²] + 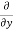 [2xy] -
[2xy] -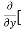 8x] +
8x] + 4y] -
4y] - 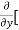 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Example2 - Calculate 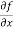 and
and 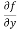 for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Solution- : To calculate 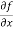 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,

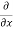 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)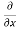 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50) cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
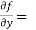
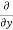 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)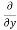 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Example3- Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Solution- 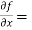 3x²y² - y⁵,
3x²y² - y⁵,  2x³y – 5xy⁴,
2x³y – 5xy⁴,
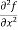 =
= 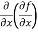 = 6xy²
= 6xy²
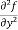 =
=  2x³ - 20xy³
2x³ - 20xy³
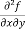 =
=  = 6x²y – 5y⁴
= 6x²y – 5y⁴
 =
=  = 6x²y - 5y⁴
= 6x²y - 5y⁴
(a) Homegeneous function - A function f(x,y) is said to be homogeneous of degree n if,
f( kx, ky) = kⁿf(x, y)
Here, the power of k is called the degree of homogeneity.
(b) Euler’s theorem (proof)-
Statement – if u = f(x, y) be a homogeneous function in x and y of degree n , then
x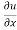 + y
+ y 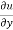 = nu
= nu
Proof: Here u is a homogeneous function of degree n,
u = xⁿ f(y/x) ----------------(1)
Partially differentiate equation (1) with respect to x,
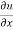 = n
= n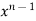 f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(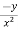 )
)
Now multiplying by x on both sides, we get
x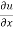 = n
= n f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(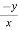 ) ---------- (2)
) ---------- (2)
Again partially differentiate equation (1) with respect to y,
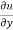 = xⁿ f’(y/x).
= xⁿ f’(y/x).
Now multiplying by y on both sides,
y  = xⁿ f’(y/x).
= xⁿ f’(y/x). ---------------(3)
---------------(3)
By adding equation (2) and (3),
x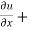 y
y 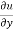 = n
= n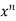 f(y/x) + + xⁿ f’(y/x).(
f(y/x) + + xⁿ f’(y/x).(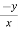 ) + xⁿ f’(y/x).
) + xⁿ f’(y/x).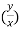
x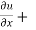 y
y 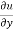 = n
= n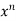 f(y/x)
f(y/x)
Here u = f( x, y) is homogeneous function, then - u =  f(y/x)
f(y/x)
Put the value of u in equation (4),
x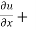 y
y 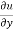 = nu
= nu
Which is the Euler’s theorem.
Lets understand Eulers’s theorem by some examples:
Example1- If u = x²(y-x) + y²(x-y), then show that 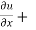
 -2 (x – y)²
-2 (x – y)²
Solution - here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
Now differentiate u partially with respect to x and y respectively,
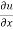 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
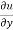 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
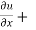
 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Example2- If u = xy + sin(xy), show that 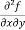 =
=  .
.
Solution – u = xy + sin(xy)
 = y+ ycos(xy)
= y+ ycos(xy)
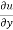 = x+ xcos(xy)
= x+ xcos(xy)
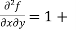 x (- sin(xy).(y)) + cos(xy)
x (- sin(xy).(y)) + cos(xy)
= 1 – xysin(xy) + cos(xy) -------------- (1)
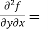 1 + cos(xy) + y(-sin(xy) x)
1 + cos(xy) + y(-sin(xy) x)
= 1 – xy sin(xy) + cos(xy) -----------------(2)
From equation (1) and (2),
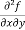 =
= 
When we measure the rate of change of the dependent variable owing to any change in a variable on which it depends, when none of the variable is assumed to be constant.
Let the function, u = f( x, y), such that x = g(t) , y = h(t)
Then we can write,
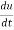 =
= 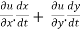
= 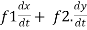
This is the total derivative of u with respect to t.
Example1: let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find 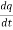 .
.
Solution: 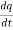 . =
. = 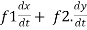
Where, f1 =  , f2 =
, f2 = 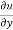
In this example f1 = 4 , f2 = 3
Also, 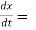 3t² + 2t ,
3t² + 2t , 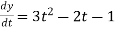
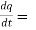 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(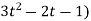
= 21t² + 2t – 3
Example2: Find 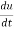 if u = x³y⁴ where x = t³ and y = t².
if u = x³y⁴ where x = t³ and y = t².
Solution: as we know that by definition, 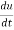 =
= 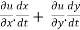
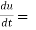 3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
If w = f (x, y) has continuous partial variables fx and fy and if x = x (t), y = y (t) are
Differentiable functions of t, then the composite function w = f (x (t), y (t)) is a
Differentiable function of t.
In this case, we get,
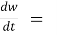 fx (x (t), y (t)) x’ (t) + fy (x(t), y (t)) y’ (t).
fx (x (t), y (t)) x’ (t) + fy (x(t), y (t)) y’ (t).
Example1: if w = x² + y – z + sint and x + y = t, find
(a)  y,z
y,z
(b) 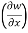 t, z
t, z
Solution: With x, y, z independent, we have
t = x + y, w = x² + y - z + sin (x + y).
Therefore,
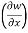 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)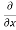 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
Thus 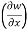 t, z = 2x - 1
t, z = 2x - 1