UNIT 6
Jacobian
If u and v are functions of the two independent variables x and y , then the determinant,

Is known as the jacobian of u and v with respect to x and y, and it can be written as,

Suppose there are three functions u , v and w of three independent variables x , y and z then,
The Jacobian can be defined as,
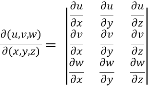
Important properties of the Jacobians-
Property-1-
If u and v are the functions of x and y , then
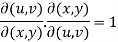
Proof- Suppose u = u(x,y) and v = v(x,y) , so that u and v are the functions of x and y,
Now,
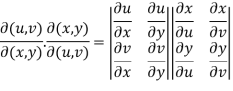
Interchange the rows and columns of the second determinant, we get
= 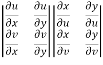
= 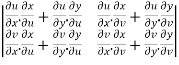 ………….(1)
………….(1)
Differentiate u = u(x,y) and v= v(x,y) partially w.r.t. u and v, we get
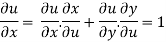

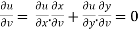

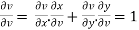


Putting these values in eq.(1) , we get
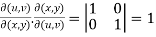 hence proved.
hence proved.
Property-2:
Suppose u and v are the functions of r and s, where r,s are the fuctions of x , y, then,
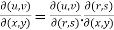
Proof: 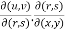 =
= 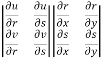
Interchange the rows and columns in second determinant
We get,
= 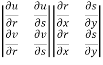
= 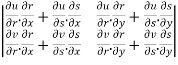
= 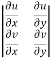 =
= 
Similarly we can prove for three variables.
Property-3
If u,v,w are the functions of three independent variables x,y,z are not independent , then,
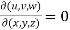
Proof: here u,v,w are independent , then f(u,v,w) = 0 ……………….(1)
Differentiate (1), w.r.t. x, y and z , we get
 …………(2)
…………(2)
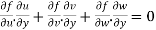 ………………(3)
………………(3)
 ………………..(4)
………………..(4)
Eliminate 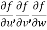 from 2,3,4 , we get
from 2,3,4 , we get
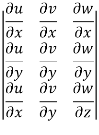
Interchanging rows and columns , we get

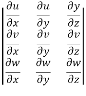 = 0
= 0
So that,
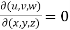
Example-1: If x = r sin , y = r sin
, y = r sin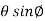 , z = r cos
, z = r cos , then show that
, then show that
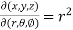 sin
sin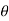 also find
also find 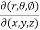
Sol. We know that,
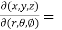

= 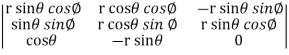
= 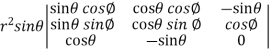
=  ( on solving the determinant)
( on solving the determinant)
= 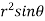
Now using first propert of Jacobians, we get
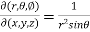
Example-2: If u = x + y + z , uv = y + z , uvw = z , find 
Sol. Here we have,
x = u – uv = u(1-v)
y = uv – uvw = uv( 1- w)
And z = uvw
So that,
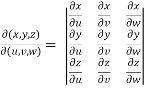
 =
=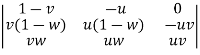
Apply 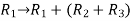
=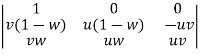
Now we get,
= u²v(1-w) + u²vw
= u²v
Example-3: If u = xyz , v = x² + y² + z² and w = x + y + z, then find J = 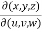
Sol. Here u ,v and w are explicitly given , so that first we calculate
J’ = 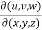
J’ = 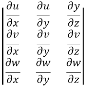 =
= 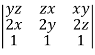
= yz(2y-2z) – zx(2x – 2z) + xy (2x – 2y) = 2[yz(y-z)-zx(x-z)+xy(x-y)]
= 2[x²y - x²z - xy² + xz² + y²z - yz²]
= 2[x²(y-z) - x(y² - z²) + yz (y – z)]
= 2(y – z)(z – x)(y – x)
= -2(x – y)(y – z)(z – x)
By the property,
JJ’ = 1
J = 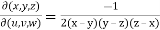
Suppose w = f(x,y) has continuous partial variables fx and fy and if x = x(t) and y = y(t) are differentiable function of t , then the composite function w = f(x(t), y(t)) is a differentiable function of t. we get,
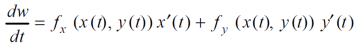
Or,
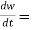

Suppose w = f(x,y,z) has continuous partial variables fx , fy and fz and if x = x(t) and y = y(t) and z = z(t) are differentiable function of t , then the composite function w = f(x(t), y(t), z(t)) is a differentiable function of t. we get,
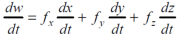
Or
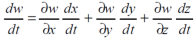
Example-1: If w = x² + y – z + sin t and x + y = t then find
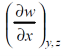
Sol. With x, y and z independent , we have
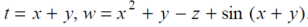
Therefore , we get
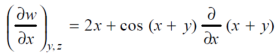
= 2x + cos ( x+ y)
Example-2: If w = x² + y – z + sin t and x + y = t then find
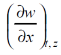
Sol. With x, t and z dependent , we have
y = t – x , w = x² + ( t – x ) + sin t
So that,

Chain rule (Jacobians)-
Suppose u and v are the functions of r and s where r,s are the functions of x, y.
Then, according chain rule-
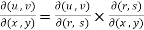
Similarly for three variables-
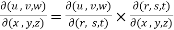
Which is also called the second property of Jacobians.
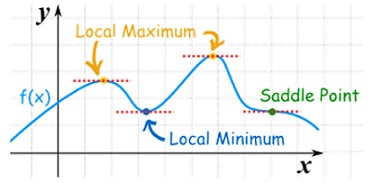
As we know that the value of a function at maximum point is called maximum value of a function. Similarly the value of a function at minimum point is called minimum value of a function.
The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complement of each other.
Maxima and Minima of a function of one variables
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point  if and only if
if and only if 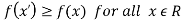
Minima is a minimum point 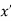 if and only if
if and only if 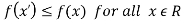


Maxima and Minima of a function of two independent variables
Let 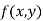 be a defined function of two independent variables.
be a defined function of two independent variables.
Then the point 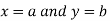 is said to be a maximum point of
is said to be a maximum point of 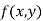 if
if
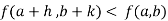
Or 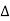 =
= 
For all positive and negative values of h and k.
Similarly the point 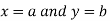 is said to be a minimum point of
is said to be a minimum point of 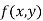 if
if
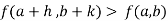
Or 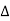 =
= 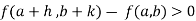
For all positive and negative values of h and k.
Saddle point:Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643164222_337592.png)
At the point.
Stationary Value
The value 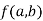 is said to be a stationary value of
is said to be a stationary value of 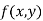 if
if

i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of 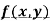
- Calculate
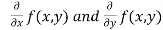 .
. - Form and solve
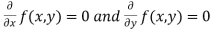 , we get the value of x and y let it be pairs of values
, we get the value of x and y let it be pairs of values 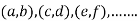
- Calculate the following values :
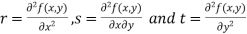
4. (a) If 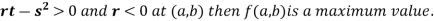
(b) If 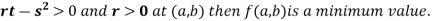
(c) If 
(d) If 
Example1 Find out the maxima and minima of the function

Given 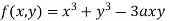 …(i)
…(i)
Partially differentiating (i) with respect to x we get
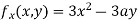 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
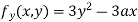 ….(iii)
….(iii)
Now, form the equations 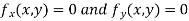
Using (ii) and (iii) we get
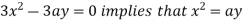
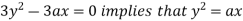
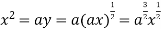 using above two equations
using above two equations
Squaring both side we get
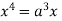
Or 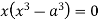
This show that 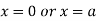
Also we get 
Thus we get the pair of value as 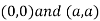
Now, we calculate
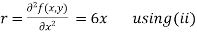
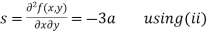
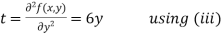
Putting above values in
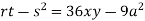
At point (0,0) we get
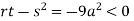
So, the point (0,0) is a saddle point.
At point 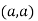 we get
we get
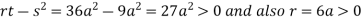
So the point 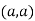 is the minimum point where
is the minimum point where 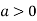
In case 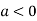
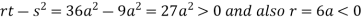
So the point 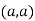 is the maximum point where
is the maximum point where 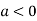
Example2 Find the maximum and minimum point of the function
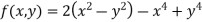
Partially differentiating given equation with respect to and x and y then equate them to zero
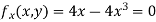

On solving above we get 
Also 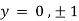
Thus we get the pair of values (0,0), (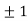 ,0) and (0,
,0) and (0,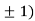
Now, we calculate
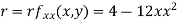
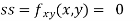

At the point (0,0)
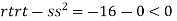
So function has saddle point at (0,0).
At the point (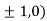
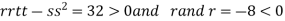
So the function has maxima at this point (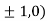 .
.
At the point (0,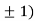

So the function has minima at this point (0, .
.
At the point (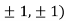
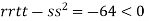
So the function has an saddle point at (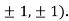
Example3 Find the maximum and minimum value of 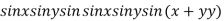
Let 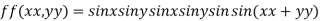
Partially differentiating given function with respect to x and y and equate it to zero
 ..(i)
..(i)
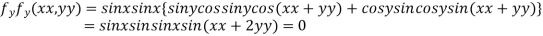 ..(ii)
..(ii)
On solving (i) and (ii) we get
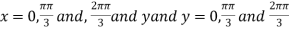
Thus pair of values are 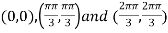
Now, we calculate

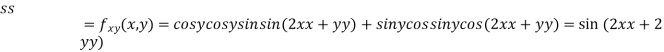
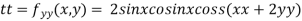
At the point (0,0)
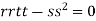
So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x, 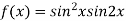
At the point 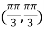
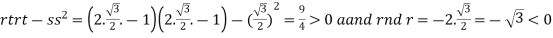
So that the given function has maximum value at 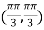
Therefore maximum value of given function
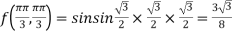
At the point 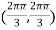
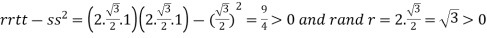
So that the given function has minimum value at 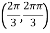
Therefore minimum value of the given function
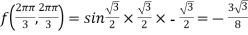
Generally to calculate the stationary value of a function with some relation by converting the given function into the least possible independent variables and then solve them. When this method fail we use Lagrange’s method.
This method is used to calculate the stationary value of a function of several variables which are all not independent but are connected by some relation.
Let 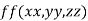 be the function in the variable x, y and z which is connected by the relation
be the function in the variable x, y and z which is connected by the relation 
Rule: a) Form the equation
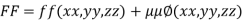
Where 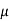 is a parameter.
is a parameter.
b) Form the equation using partial differentiation is
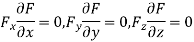
(We always try to eliminate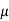 )
)
c) Solve the all above equation with the given relation 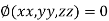
These give the value of 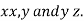
These value obtained when substituted in the given function will give the stationary value of the function.
Example1 Divide 24 into three parts such that the continued product of the first, square of second and cube of third may be maximum.
Let first number be x, second be y and third be z.
According to the question
Let the given function be f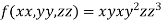
And the relation 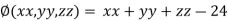
By Lagrange’s Method
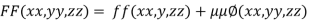
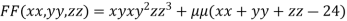 ….(i)
….(i)
Partially differentiating (i) with respect to x,y and z and equate them to zero

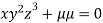 ….(ii)
….(ii)
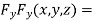
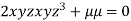 ….(iii)
….(iii)
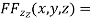
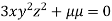 ….(iv)
….(iv)
From (ii),(iii) and (iv) we get
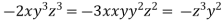
On solving
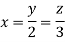
Putting it in given relation we get
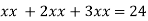
Or 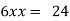
Or 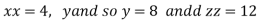
Thus the first number is 4 second is 8 and third is 12
Example2 The temperature T at any point  in space is
in space is 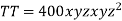 .Find the highest temperature on the surface of the unit sphere.
.Find the highest temperature on the surface of the unit sphere.
Given function is 
On the surface of unit sphere given 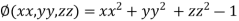 [
[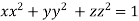 is an equation of unit sphere in 3 dimensional space]
is an equation of unit sphere in 3 dimensional space]
By Lagrange’s Method
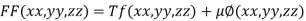
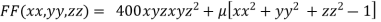 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
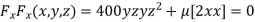 or
or 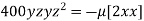 …(ii)
…(ii)
 or
or 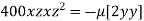 …(iii)
…(iii)
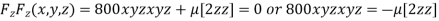 …(iv)
…(iv)
Dividing (ii) and (ii) by (iv) we get
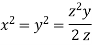
Using given relation 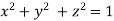
Or 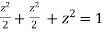 Or
Or 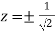
So that 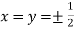
Or 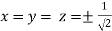
Thus points are 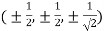
The maximum temperature is 
Example3 If 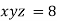 ,Find the value of x and y for which
,Find the value of x and y for which 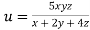 is maximum.
is maximum.
Given function is 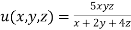
And relation is 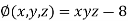
By Lagrange’s Method
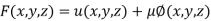
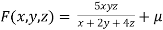 [
[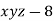 ] ..(i)
] ..(i)
Partially differentiating (i) with respect to x, y and z and equate them tozero
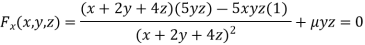
Or 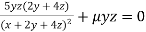 …(ii)
…(ii)
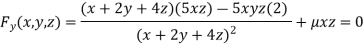
Or  …(iii)
…(iii)
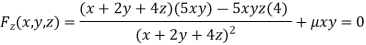
Or 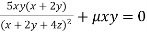 …(iv)
…(iv)
On solving (ii),(iii) and (iv) we get

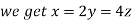
Using the given relation we get 

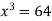
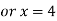
So that 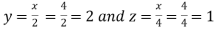
Thus the point for the maximum value of the given function is 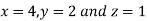
Example4 Find the points on the surface  nearest to the origin.
nearest to the origin.
Let 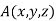 be any point on the surface, then its distance from the origin
be any point on the surface, then its distance from the origin  is
is
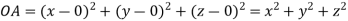
Thus the given equation will be
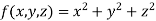
And relation is 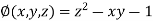
By Lagrange’s Method
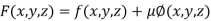
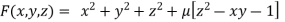 ….(i)
….(i)
Partially differentiatig (i) with respect to x, y and z and equate them to zero
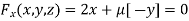
Or 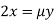 …(ii)
…(ii)
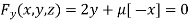
Or 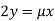 …(iii)
…(iii)

Or 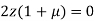
Or 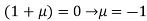
On solving equation (ii) by (iii) we get

And 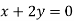
On subtracting we get 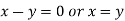
Putting in above 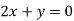
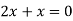 Or
Or 
Thus 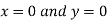
Using the given relation we get
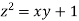 = 0.0 +1=1
= 0.0 +1=1
Or 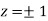
Thus point on the surface nearest to the origin is