UNIT-5
Partial differentiation
First order partial differentiation-
Let f(x , y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as 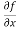 and defined as follows:
and defined as follows:
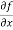 =
= 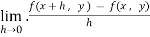
Now the partial derivative of f with respect to f can be written as 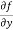 and defined as follows:
and defined as follows:
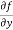 =
= 
Note: a. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating, as constant.
b. We apply all differentiation rules.
Higher order partial differentiation-
Let f(x , y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives.
These are second order four partial derivatives:
(a)  =
= 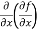
(b) 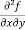 =
= 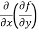
(c) 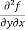 =
= 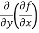
(d) 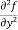 =
= 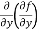
b and c are known as mixed partial derivatives.
Similarly we can find the other higher order derivatives.
Example-1: - Calculate 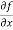 and
and 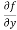 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate 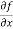 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
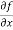 =
= 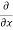 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 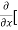 3x³] -
3x³] -  5y²] +
5y²] + 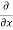 [2xy] -
[2xy] -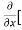 8x] +
8x] +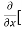 4y] -
4y] - 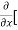 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
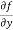 =
= 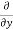 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 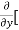 3x³] -
3x³] - 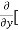 5y²] +
5y²] + 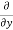 [2xy] -
[2xy] -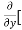 8x] +
8x] +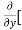 4y] -
4y] - 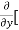 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Example-2: Calculate  and
and 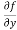 for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Sol. To calculate 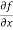 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
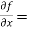
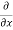 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)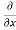 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50) cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
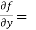
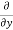 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)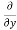 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Example-3: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Sol. 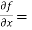 3x²y² - y⁵,
3x²y² - y⁵, 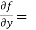 2x³y – 5xy⁴,
2x³y – 5xy⁴,
 =
= 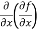 = 6xy²
= 6xy²
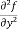 =
= 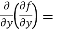 2x³ - 20xy³
2x³ - 20xy³
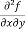 =
= 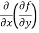 = 6x²y – 5y⁴
= 6x²y – 5y⁴
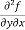 =
= 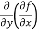 = 6x²y - 5y⁴
= 6x²y - 5y⁴
Example-4: Find
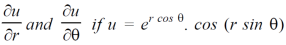
Sol. First we will differentiate partially with respect to r,
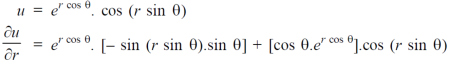
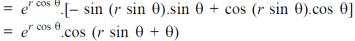
Now differentiate partially with respect to θ, we get
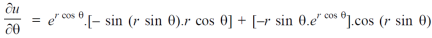
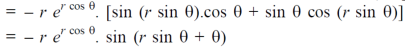
Example-5: if,
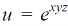
Then find.
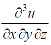
Sol-
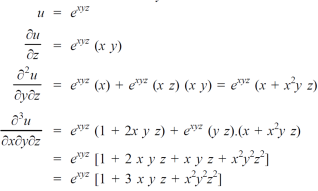
Example-6: if  , then show that-
, then show that- 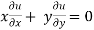
Sol. Here we have,
u = 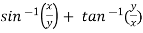 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get
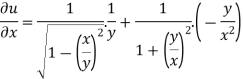
= 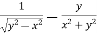
Or
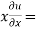
 ………………..(2)
………………..(2)
And now,


= 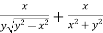
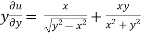 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
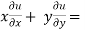
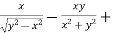
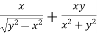 = 0
= 0
Hence proved.
When we measure the rate of change of the dependent variable owing to any change in a variable on which it depends, when none of the variable is assumed to be constant.
Let the function, u = f( x, y), such that x = g(t) , y = h(t)
ᵡ Then we can write,
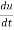 =
= 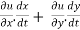
= 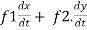
This is the total derivative of u with respect to t.
Change of variable-
If w = f (x, y) has continuous partial variables fx and fy and if x = x (t), y = y (t) are
Differentiable functions of t, then the composite function w = f (x (t), y (t)) is a
Differentiable function of t.
In this case, we get,
 fx (x (t), y (t)) x’ (t) + fy (x(t), y (t)) y’ (t).
fx (x (t), y (t)) x’ (t) + fy (x(t), y (t)) y’ (t).
Example-:1 let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find 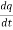 .
.
Sol. :  . =
. = 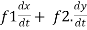
Where, f1 = 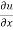 , f2 =
, f2 = 
In this example f1 = 4 , f2 = 3
Also, 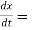 3t² + 2t ,
3t² + 2t , 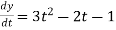
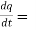 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(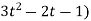
= 21t² + 2t – 3
Example-2: Find 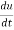 if u = x³y⁴ where x = t³ and y = t².
if u = x³y⁴ where x = t³ and y = t².
Sol. As we know that by definition, 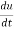 =
= 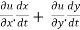
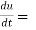 3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
Example-3: if w = x² + y – z + sin t and x + y = t, find
(a) 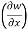 y,z
y,z
(b) 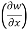 t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x² + y - z + sin (x + y).
Therefore,
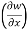 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)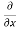 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
Thus 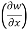 t, z = 2x - 1
t, z = 2x - 1
Example-4: If u = u( y – z , z - x , x – y) then prove that 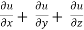 = 0
= 0
Sol. Let,
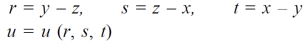
Then,
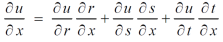
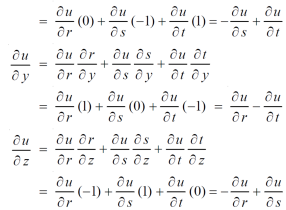
By adding all these equations we get,
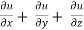 = 0 hence proved.
= 0 hence proved.
Example-5: if φ( cx – az , cy – bz) = 0 then show that ap + bq = c
Where p =  q =
q = 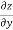
Sol. We have,
φ( cx – az , cy – bz) = 0
φ( r , s) = 0
Where,
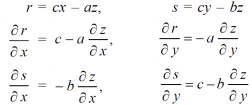
We know that,

Again we do,

By adding the two results, we get


Example-6: If z is the function of x and y , and x = 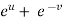 , y =
, y = 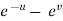 , then prove that,
, then prove that,
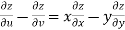
Sol. Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
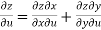 ……………….(1)
……………….(1)
And,
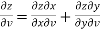 ………………..(2)
………………..(2)
Also there is,
x = 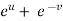 and y =
and y = 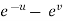 ,
,
Now,
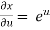 ,
, 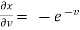 ,
, 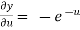 ,
, 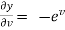
From equation(1) , we get
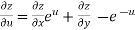 ……………….(3)
……………….(3)
And from eq. (2) , we get
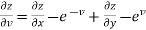 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
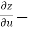
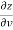 =
= 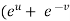 )
) 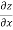 – (
– (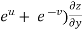
= x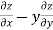
Hence proved.
Before Euler’s theorem, we will go through homogeneous functions,
(a) Homogeneous function - A function f(x,y) is said to be homogeneous of degree n if,
f( kx, ky) = kⁿf(x, y)
Here, the power of k is called the degree of homogeneity.
(b) Euler’s theorem-
Statement – if u = f(x, y) be a homogeneous function in x and y of degree n , then
x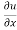 + y
+ y  = nu
= nu
Proof: Here u is a homogeneous function of degree n,
u = xⁿ f(y/x) ----------------(1)
Partially differentiate equation (1) with respect to x,
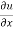 = n
= n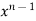 f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(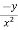 )
)
Now multiplying by x on both sides, we get
x = n
= n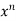 f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(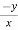 ) ---------- (2)
) ---------- (2)
Again partially differentiate equation (1) with respect to y,
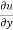 = xⁿ f’(y/x).
= xⁿ f’(y/x).
Now multiplying by y on both sides,
y 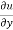 = xⁿ f’(y/x).
= xⁿ f’(y/x). ---------------(3)
---------------(3)
By adding equation (2) and (3),
x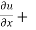 y
y 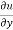 = n
= n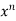 f(y/x) + + xⁿ f’(y/x).(
f(y/x) + + xⁿ f’(y/x).(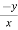 ) + xⁿ f’(y/x).
) + xⁿ f’(y/x).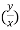
x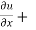 y
y 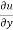 = n
= n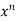 f(y/x)
f(y/x)
Here u = f( x, y) is homogeneous function, then - u = 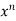 f(y/x)
f(y/x)
Put the value of u in equation (4),
x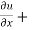 y
y 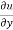 = nu
= nu
Which is the Euler’s theorem.
Lets understand Eulers’s theorem by some examples:
Example1- If u = x²(y-x) + y²(x-y), then show that 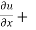
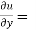 -2 (x – y)²
-2 (x – y)²
Solution - here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
Now differentiate u partially with respect to x and y respectively,
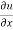 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
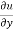 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
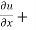
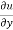 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Example2- If u = xy + sin(xy), show that 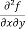 =
= 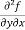 .
.
Solution – u = xy + sin(xy)
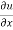 = y+ ycos(xy)
= y+ ycos(xy)
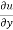 = x+ xcos(xy)
= x+ xcos(xy)
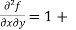 x (- sin(xy).(y)) + cos(xy)
x (- sin(xy).(y)) + cos(xy)
= 1 – xysin(xy) + cos(xy) -------------- (1)
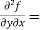 1 + cos(xy) + y(-sin(xy) x)
1 + cos(xy) + y(-sin(xy) x)
= 1 – xy sin(xy) + cos(xy) -----------------(2)
From equation (1) and (2),
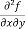 =
= 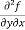
Example-3: If u(x,y,z) = log( tan x + tan y + tan z) , then prove that ,
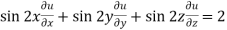
Sol. Here we have,
u(x,y,z) = log( tan x + tan y + tan z) ………………..(1)
Diff. Eq.(1) w.r.t. x , partially , we get
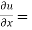
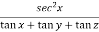 ……………..(2)
……………..(2)
Diff. Eq.(1) w.r.t. y , partially , we get
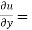
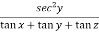 ………………(3)
………………(3)
Diff. Eq.(1) w.r.t. z , partially , we get

 ……………………(4)
……………………(4)
Now multiply eq. 2 , 3 , 4 by sin 2x , sin 2y , sin 2z respectively and adding , in order to get the final result,
We get,
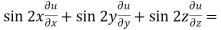
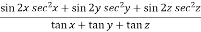
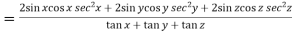
= 
So that,
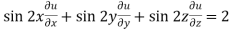 hence proved.
hence proved.
Let us suppose we have,
z = f(x , y)
Where, x = g(u , v)
And y = h(u , v)
Then,

And
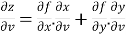
Let’s do some examples-
Example-1: If u = u(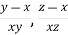 ), then prove that
), then prove that 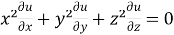 .
.
Sol. We are given that,
u = u (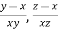 ) = u( r , s)
) = u( r , s)
Where r = 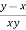 and s =
and s = 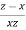
Or we can write as-
r = 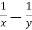 and s =
and s = 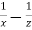
Differentiate them partially with respect to x , y and z. , we get
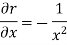

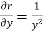

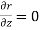

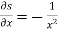

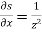

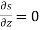
As we know that-

Then,
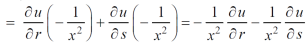


Adding all these results, we get
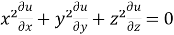 .
.
Example-2: If u = x³ + y³ where x = a cos t and y = b sin t , then find du/dt.
Sol. Given,
u = x³ + y³
x = a cos t and y = b sin t
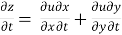
= (3x²)(-a sint) + (3y²) (b cost)
= -3a³cos²t sint + 3b³sin²t cost