UNIT-4
Successive Differentiation
Successive differentiation-
The successive differential coefficients of y are denoted as follows-
……………….
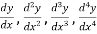The 
differential coefficient is- 
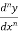
Other notations to denote n’th differential coefficients-
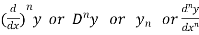
The process of applying differentiation again and again is called successive differentiation.
nth derivative of standard functions-
1. nth derivative of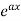 
–
Suppose y =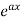 
,
Differentiate with respect to x successively, we get
.
.
.
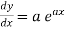
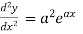
For n times differentiation, we get-
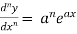
So we can say that its n’th derivative will be
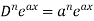
2. nth derivative of log(ax + b)-
Suppose y = log (ax + b)
Differentiate with respect to x successively, we get
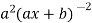
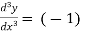(-2)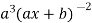 
.
.
.
For n times differentiation, we get-
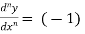(-2)…………….(-n + 1) 
= 
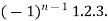…………….(n - 1)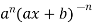 
= 
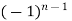(n - 1)
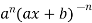
So we can say that its n’th derivative will be
3. nth derivative of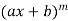 
-
Suppose y =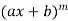 
Differentiate with respect to x successively, we get
.
.
.
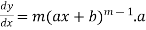
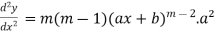
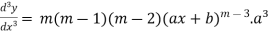
For n times differentiation, we get-
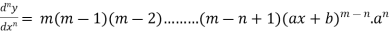
So we can say that its n’th derivative will be
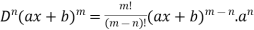
4. nth derivative of sin(ax + b)-
Suppose y = sin(ax + b)
Differentiate with respect to x successively, we get
.
.
.
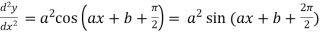
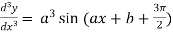
For n times differentiation, we get-
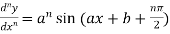
So we can say that its n’th derivative will be
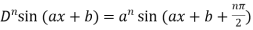
Similarly we can find the ‘n’ derivatives of such functions-
Example-1: Find the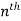 
derivative of the following function-
Sol. Partial fraction of the function y after splitting-
Suppose x – 1 = z, then
= 
= 
= 
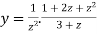
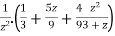
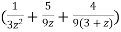
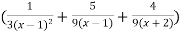
Here we can find its n’th derivative-
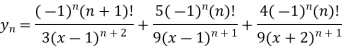
Example-2: If y =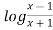 
, then show that-
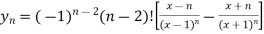
Sol. We have,
y =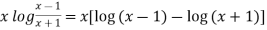 
Differentiate y with respect to x, we get
= 
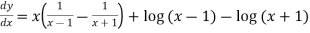
Again diff. (n – 1) times w.r .t x , we get-
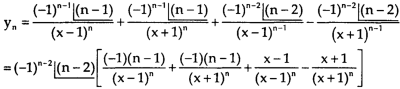
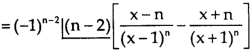
Leibnitz Theorem-
If u and v are the functions of x, then-
+……….+
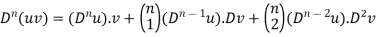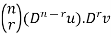+…….+ u.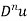
Example-3: If 
, then prove that-
Sol. Here it is given that-
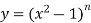
On differentiating-
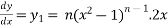
Or
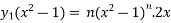
= ny.2x
Differentiate again with respect to x, we get-
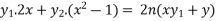
Or
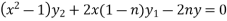…………………. (1)
Differentiate each term of (1) by using Leibnitz’s theorem, we get-
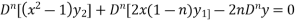
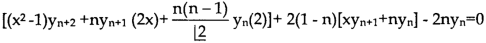
Therefore we get-
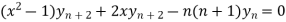
Hence proved.
Example-4: If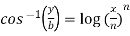 
, then prove that-
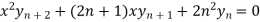
Sol. Here we have-
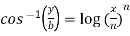
Or
Or
y = b cos[ n log(x/n)]
On differentiating, we get-
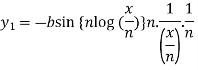
Which becomes-
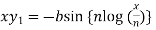
Differentiate again both sides with respect to x, we get-
It becomes-
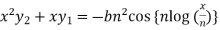
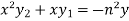
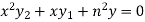……………….. (1)
Differentiate each term n times with respect to x, we get-
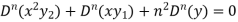
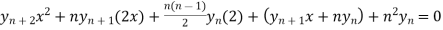
Which is-
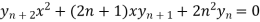hence proved,
Taylor’s Theorem-
If f(x + h) is a function of h which can be expanded in the ascending powers of h and is differentiable by any number of times with respect to h, then-
+ …….+ 
+ ……..
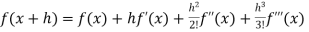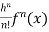Which is called Taylor’s theorem.
If we put x = a, we get-
+ …….+ 
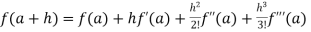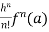+ …….. (1)
Maclaurin’s Theorem-
If we put a = 0 and h = x then equation(1) becomes-
+ …….
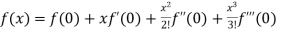Which is called Maclaurin’s theorem.
Note – if we put h = x - a then there will be the expansion of F(x) in powers of (x – a)
We get-
+ …….
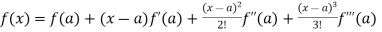Example-1: Express the polynomial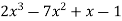 
in powers of (x-2).
Sol. Here we have,
f(x) =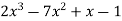 
Differentiating the function w.r.t.x-
f’(x) =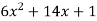 
f’’(x) = 12x + 14
f’’’(x) = 12
f’’’’(x)=0
Now using Taylor’s theorem-
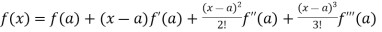+ ……. (1)
Here we have, a = 2,
Put x = 2 in the derivatives of f(x), we get-
f(2) =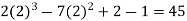 
f’(2) =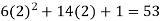 
f’’(2) = 12(2)+14 = 38
f’’’(2) = 12 and f’’’’(2) = 0
Now put a = 2 and substitute the above values in equation(1), we get-
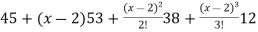
Taylor’s theorem for functions of two variables-
Suppose f(x , y) be a function of two independent variables x and y. Then,
+ ……………
Maclaurin’s series is the special case of Taylor’s series-
When we put a = 0 and b = 0 (about origin) in Taylor’s series, we get-
+ ……………
Example-2: Expand f(x , y) =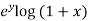 
in powers of x and y about origin.
Sol. Here we have the function-
f(x , y) =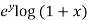 
Here , a = 0 and b = 0 then
f(0 , 0) = 
Now we will find partial derivatives of the function-
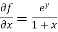
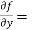
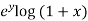
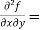
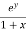
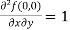
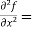
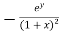
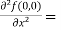
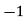
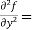
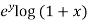
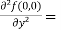
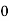
Now using Taylor’s theorem-
+………
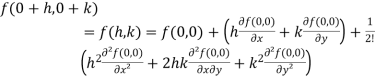Suppose h = x and k = y , we get
+…….
= 
+……….
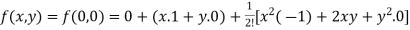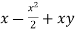Example-3: Find the Taylor’s expansion of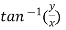 
about (1 , 1) up to second degree term.
Sol. We have,
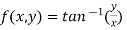
At (1 , 1)
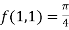
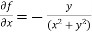
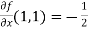
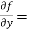
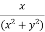
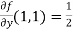
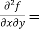
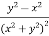
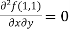
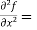
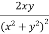
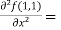
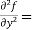
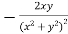
Now by using Taylor’s theorem-
……
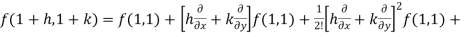Suppose 1 + h = x then h = x – 1
1 + k = y then k = y - 1
……
= 
……..
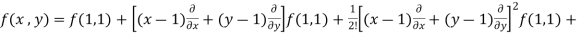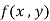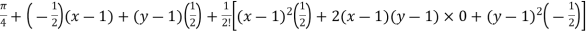
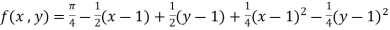Example-1: Calculate log [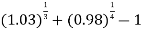 
]approximately by using Taylor’s expansion.
Sol. Suppose- f(x , y) = log [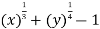 
]
f(1 , 1) = log 1 = 0
Now we will find out the derivatives- take a = 1 and b = 1
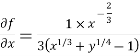
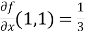
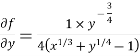
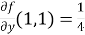
Using Taylor’s theorem-
+ ……………….
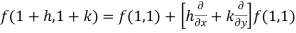But here,
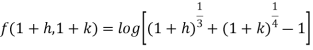
So that-
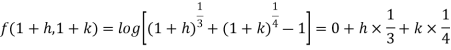
Put h = 0.03 and k = -0.02 , we get
Example-2: Expand 
near the point (1 , π/4) by using Taylor’s theorem.
Sol. Let f(x , y) =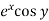 
We know that,
+ ……………
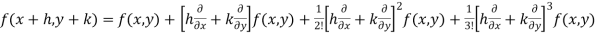Then,
f(x , y) =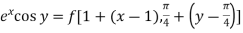 
Where h = x – 1 and k =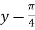 
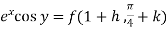
So that,
f(x , y) =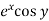 
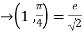
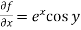
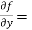
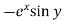
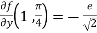
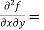
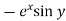
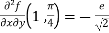
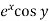
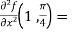
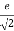
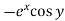
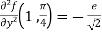
Put the above values in Taylor’s expansion-
+………
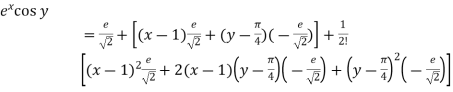Let we have two functions f(x) and g(x) and-
Then-
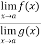is an expression of the form 
, in that case we can say that f(x)/g(x) is an indeterminate for of the type 
at x = a.
Now, Let we have two functions f(x) and g(x) and-
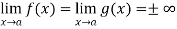
Then-
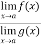is an expression of the form 
, in that case we can say that f(x)/g(x) is an indeterminate for of the type 
at x = a.
Some other indeterminate forms are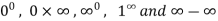 
L’Hospital’s rule for 
form-
Working steps-
1. Check that the limits f(x)/g(x) is an indeterminate form of type 
.
(note- we cannot apply L’Hospital rule if it is not in indeterminate form)
2. Differentiate f and g separately.
3. Find the limits of the derivatives. If the limit is finite,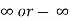 
then it is equal to the limit of f(x)/g(x).
Example-1: Evaluate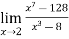 
Sol. Here we notice that it is an indeterminate form of 
.
So that , we can apply L’Hospital rule-
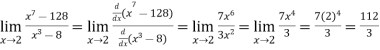
Example-2: Evaluate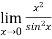 
.
Sol. Let f(x) =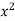 
and g(x) = 
.
Here we see that this is the indeterminate form of 0/0 at x = 0.
Now by using L’Hospital rule, we get-
= 
= 
= 
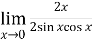
= 1
Note- Suppose we get an indeterminate form even after finding first derivative, then in that case , we use the other form of L’Hospital’s rule.
If we have f(x) and g(x) are two functions such that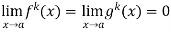 
.
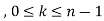If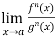 
exist or (∞ , -∞), then
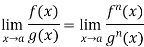
Example-3: Evaluate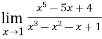 
Sol. Let f(x) =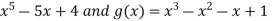 
, then
And
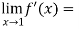
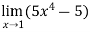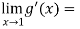
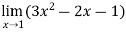= 0
= 0
But if we use L’Hospital rule again, then we get-
Example-4: Evaluate 
Sol. We can see that this is an indeterminate form of type 0/0.
Apply L’Hospital’s rule, we get
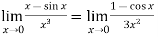
But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-
We get
= 
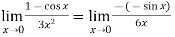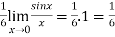
L’Hospital’s rule for 
form-
Let f and g are two differentiable functions on an open interval containing x = a, except possibly at x = a and that
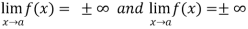
If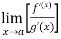 
has a finite limit, or if it is 
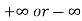, then
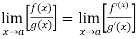
Theorem- If we have f(x) and g(x) are two functions such that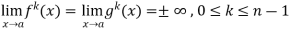 
.
If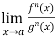 
exist or (∞ , -∞), then
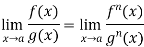
Example-5: Find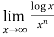 
, n>0.
Sol. Let f(x) = log x and g(x) =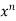 
These two functions satisfied the theorem that we have discussed above-
So that,
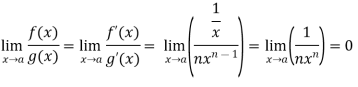
Example-6: Evaluate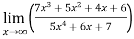 
Sol. Apply L’Hospital rule as we can see that this is the form of 
= 
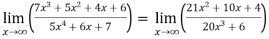Example-7:
Note- In some cases like above example, we can not apply L’Hospital’s rule.
Other types of indeterminate forms-
Example-8: Evaluate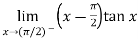 
Sol. Here we find that-
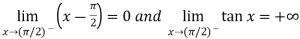
So that this limit is the form of 0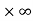
.
Now,
Change 
to obtain the limit-
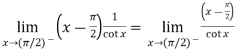
Now this is the form of 0/0,
Apply L’Hospital’s rule-
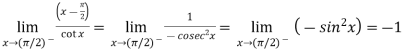
Power series-
The following series in x is called power series -
……..
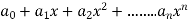Here a’s are the independent of x.
Ratio test-
Statement- suppose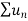 
is a series of positive terms such that 
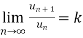then,
1. If k<1 , the series will be convergent.
2. If k>1 , then the series will be divergent.
Proof: Proof:
Case-1:
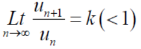
We know that from the definition of limits ,it follows,
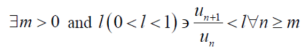
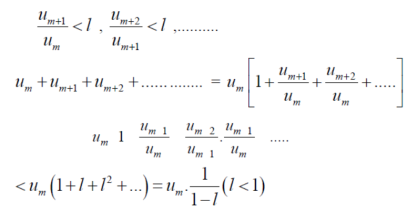
But,
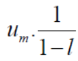
Is the finite quantity. So 
is convergent.
Case-2:
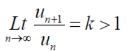
There could be some finite terms in starting which will never satisfy the condition,
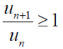
In this case we can find a number ‘m’,
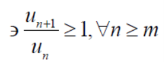
Ignoring the first ‘m’ terms, if we write the series as
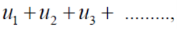
We have , in this case
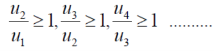
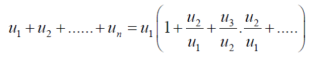
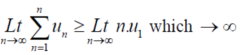
So that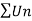 
is divergent.
Example: Test the convergence of the series whose n’th term is given below-
n’th term = 
Sol. We have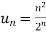 
and 
By D’Alembert ratio test,
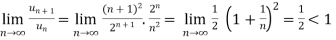
So that by D’Alembert ratio test , the series will be convergent.
Example: Test for the convergence of the n’th term of the series given below-
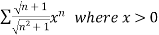
Sol. We have ,
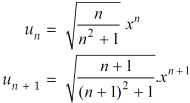
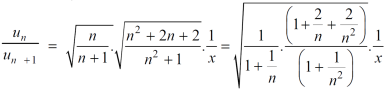
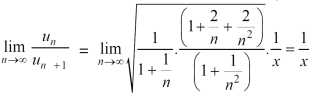
Now , by D’Almbert ratio test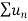 
converges if 
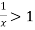and diverges if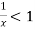 
At x = 1 , this test fails.
Now , when x = 1
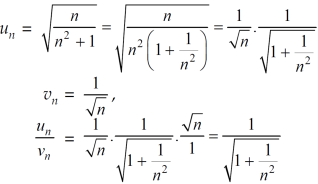
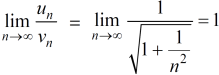
The limit is finite and not zero.
Then by comparison test,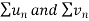 
converges or diverges together.
Since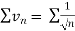 
is the form of 
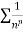, in which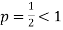 
Hence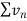 
diverges then 
will also diverge.
Therefore in the given series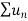 
converges if x<1 and diverges if x≥1.
(Note- please read about p-test before comparison test)
Positive term series- if all the terms in an infinite series are positive after few negative terms , then the series said to be a positive term series.
Suppose ,
-22-65+ 55 +69 99+125+………….is a positive term series.
If we remove these negative terms , then the nature of the series does not change.
Comparison test-
Statement-
Suppose we have two series of positive terms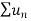 
and 
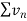then,
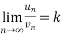, where k is a finite number , then both series converges or diverges together.
Proof- we know that by the definition of limits, there exist a positive number epsilon(ε)
Which is very small. Such that
According to definition( comparison test)
|
|< ε for n>m , that means
k-ε <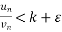 
for n>m
Ignoring the first m terms of the series,
We get
k-ε < 
for n>m for all n ………………..(1)
There will be two cases-
Case-1: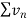 
is convergent , then
(
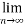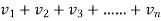) = r (say) , where r is finite number
From (1),
(
)<
(
) = 
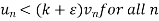
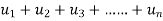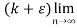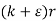
Therefore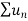 
is also convergent.
Case-2: : 
is divergent, then
(
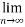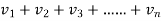)→∞ …………………………..(2)
From eq. (1)
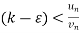
Then
(
)<
(
)
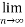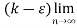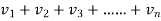From(2)
(
)→∞
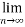Hence,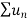 
is also divergent.
Example: Test the convergence of the following series.
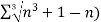
Sol. We have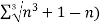 
First we will find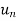 
and the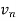 
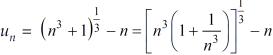
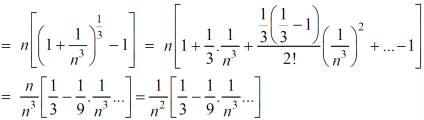
And
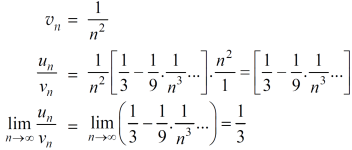
Here, we can see that, the limit is finite and not zero,
Therefore,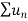 
and 
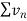converges or diverges together.
Since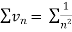 
is of the form 
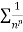where p = 2>1
So that , we can say that,
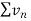is convergent , so that 
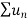will also be convergent.
Example: Test the convergence of the following series-
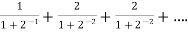
Sol. Here we have the series,
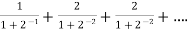
Now,
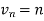
Now comapare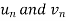 
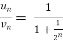
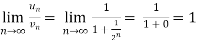
We can see that the limit is finite and not zero.
Here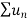 
and 
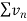converges or diverges together since ,
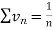is the form of 
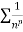here p = 1,
So that,
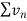is divergent then 
is also divergent.
Example: Show that the following series is convergent.
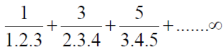
Sol.
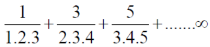
Suppose,
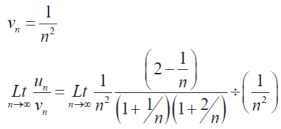
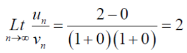
Which is finite and not zero.
By comparison test 
and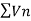 
converge or diverge together.
But,
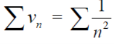
Is convergent. So that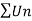 
is also convergent.
Example: Test the series:
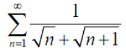
Sol. The series is,
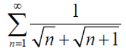
Now,
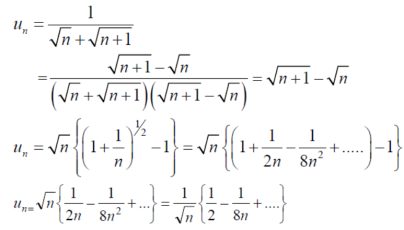
Take,
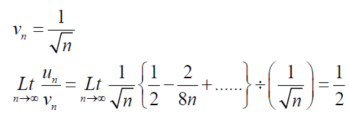
Which is finite and not zero.
Which is finite and not zero.
By comparison test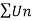 
and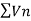 
converge or diverge together.
But,
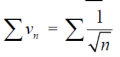
Is divergent. ( p = ½)
So that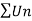 
is divergent.
4.7. Cauchy’s 
root test
Let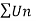 
be a series of positive terms and let
Then 
is convergent when l<1 and diverges when l >1.
Proof: case-1:
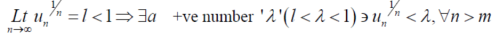
Or
Since,
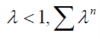
Is a geometric series with common ratio < 1 so that the series will be convergent.
Case- 2:
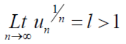
By the limit concept, we can find a number,
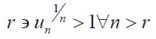
That means
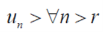
After 1st ‘r’ terms , each term is > 1
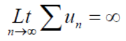
So that the series is divergent.
Example: Test the convergence of the series whose nth term is given below-
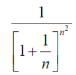
Sol.
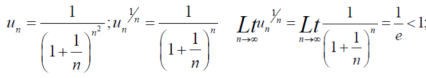
By root test 
is convergent.
Example: Test the convergence of the series whose nth term is given below-
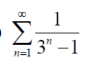
Sol.
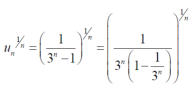
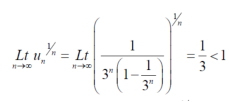
By root test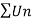 
is convergent.
Example: show that the following series is convergent.
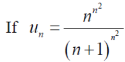
Sol.
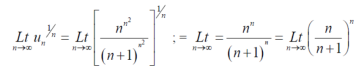
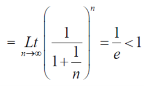
By root test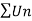 
is convergent.
Example: Test the convergence of the following series:
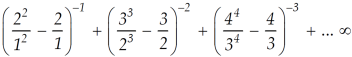
Sol. Here, we have,
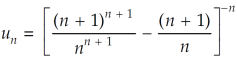
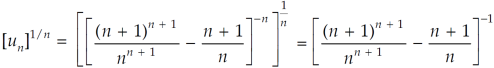
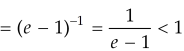
Therefore the given series is convergent.
References:
1. A Text book of Engineering mathematics (Volume-I, II), P.N. Wartikar and J.N.
Wartikar, Pune Vidyarthi Girha Prakashan, Pune.
2. Higher Engineering Mathematics by B.S. Grewal, Khanna Publications, New
Delhi.
3. Advanced Engineering Mathematics by Erwin Kreyszig, Wiley Eastern Ltd.
4. Engineering Mathematics by Babu Ram, PEARSON.
5. Engineering Mathematics A Tutorial Approach by Ravish R Singh, Mukul Bhat,
McGraw Hill
6. A Textbook of Engineering Mathematics by N.P Bali and Manish Goyal
