UNIT-2
Matrices II
Suppose we have A = 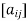 be an n × n matrix, then
be an n × n matrix, then
Characteristic equation- The equation |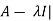 = 0 is called the characteristic equation of A , where |
= 0 is called the characteristic equation of A , where |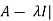 is called characteristic matrix of A. Here I is the identity matrix.
is called characteristic matrix of A. Here I is the identity matrix.
The determinant |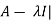 is called the characteristic polynomial of A.
is called the characteristic polynomial of A.
Characteristic roots- the roots of the characteristic equation are known as characteristic roots or Eigen values or characteristic values.
Important notes on characteristic roots-
1. The characteristic roots of the matrix ‘A’ and its transpose A’ are always same.
2. If A and B are two matrices of the same type and B is invertible then the matrices A and 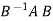 have the same characteristic roots.
have the same characteristic roots.
3. If A and B are two square matrices which are invertible then AB and BA have the same characteristic roots.
4. Zero is a characteristic root of a matrix if and only if the given matrix is singular.
Solved examples to find characteristics equation-
Example-1: Find the characteristic equation of the matrix A:
A = 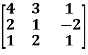
Sol. The characteristic equation will be-
|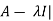 = 0
= 0
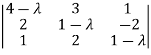 = 0
= 0
On solving the determinant, we get
(4-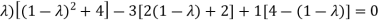
Or 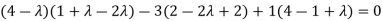
On solving we get,
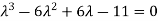
Which is the characteristic equation of matrix A.
Example-2: Find the characteristic equation and characteristic roots of the matrix A:
A = 
Sol. We know that the characteristic equation of the matrix A will be-
|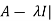 = 0
= 0
So that matrix A becomes,
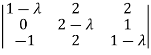 = 0
= 0
Which gives , on solving
(1-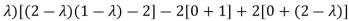 = 0
= 0
Or 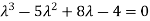
Or (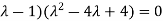
Which is the characteristic equation of matrix A.
The characteristic roots will be,
(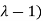 (
(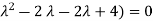
(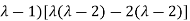
(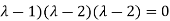
Values of 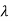 are-
are-
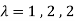
These are the characteristic roots of matrix A.
Example-3: Find the characteristic equation and characteristic roots of the matrix A:
A = 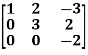
Sol. We know that, the characteristic equation is-
|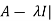 = 0
= 0
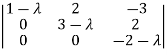 = 0
= 0
Which gives,
(1-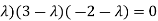
Characteristic roots are- 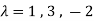
Let A is a square matrix of order n. The equation formed by
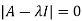
Where I is an identity matrix of order n and 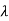 is unknown. It is called characteristic equation of the matrix A.
is unknown. It is called characteristic equation of the matrix A.
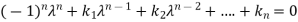
The values of the 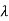 are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
Corresponding to each Eigen value there exist vectors X,
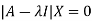
Called the characteristics vectors or latent vectors or Eigen vectors of the matrix A.
Note: Corresponding to distinct Eigen value we get distinct Eigen vectors but in case of repeated Eigen values we can have or not linearly independent Eigen vectors.
If 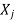 is Eigen vectors corresponding to Eigen value
is Eigen vectors corresponding to Eigen value 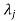 then
then 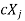 is also Eigen vectors for scalar c.
is also Eigen vectors for scalar c.
Properties of Eigen Values:
- The sum of the principal diagonal element of the matrix is equal to the sum of the all Eigen values of the matrix.
Let A be a matrix of order 3 then 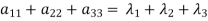
2. The determinant of the matrix A is equal to the product of the all Eigen values of the matrix then 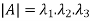 .
.
3. If 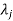 is the Eigen value of the matrix A then 1/
is the Eigen value of the matrix A then 1/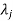 is the Eigen value of the
is the Eigen value of the 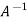 .
.
4. If 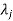 is the Eigen value of an orthogonal matrix, then 1/
is the Eigen value of an orthogonal matrix, then 1/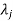 is also its Eigen value.
is also its Eigen value.
5. If 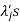 are the Eigen values of the matrix A then
are the Eigen values of the matrix A then 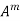 has the Eigen values
has the Eigen values 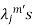 .
.
Example1: Find the sum and the product of the Eigen values of 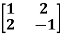 ?
?
Sol. The sum of Eigen values = the sum of the diagonal elements
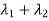 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
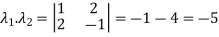
On solving above equations we get 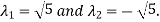
Example2: Find out the Eigen values and Eigen vectors of 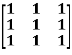 ?
?
Sol. The Characteristics equation is given by 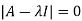
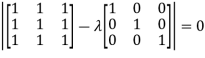
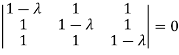
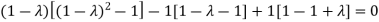
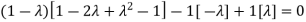
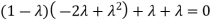
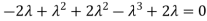
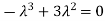
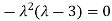
Or 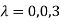
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 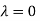 is
is
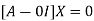
Where X is the column matrix of order 3 i.e.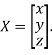
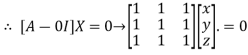
This implies that 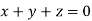
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1)=2 linearly independent solutions.
Let 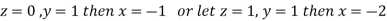
Thus the Eigen vectors corresponding to the Eigen value 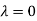 are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 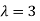 is
is
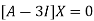
Where X is the column matrix of order 3 i.e.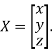
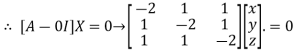
This implies that 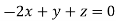
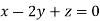
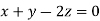
Taking last two equations we get
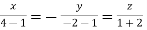
Or 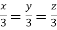
Thus the Eigen vectors corresponding to the Eigen value 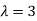 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Example3: Find out the Eigen values and Eigen vectors of 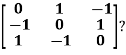
Sol. Let A =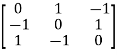
The characteristics equation of A is 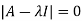 .
.
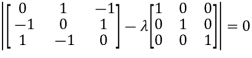
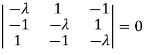
Or 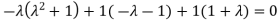
Or 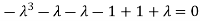
Or 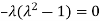
Or 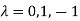
The Eigen vector corresponding to Eigen value 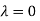 is
is
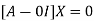
Where X is the column matrix of order 3 i.e.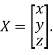
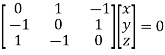
Or 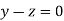
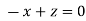
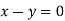
On solving we get 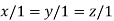
Thus the Eigen vectors corresponding to the Eigen value 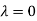 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 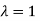 is
is
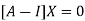
Where X is the column matrix of order 3 i.e.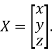
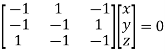
Or 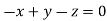
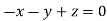
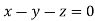
On solving 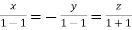 or
or 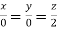 .
.
Thus the Eigen vectors corresponding to the Eigen value 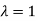 is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 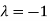 is
is
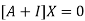
Where X is the column matrix of order 3 i.e.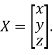
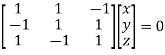
Or 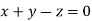
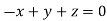
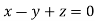
On solving we get 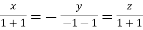 or
or 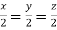 .
.
Thus the Eigen vectors corresponding to the Eigen value 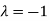 is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Cayley-Hamilton theorem states that every square matrix A when substituted in its
Characteristic’s equation, will satisfies it.
Let A is a square matrix of order n. The characteristic equation of the matrix A.
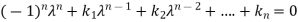
Then according to Cayley-Hamilton theorem
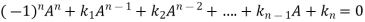
We can also find the inverse of A ,
Multiplying 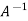 on both side of above equation we get
on both side of above equation we get
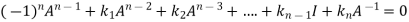
Or 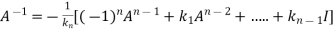
Example1: Verify the Cayley-Hamilton theorem and find the inverse.
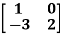 ?
?
Sol. Let A =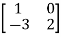
The characteristics equation of A is 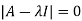
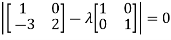
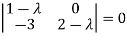
Or 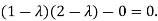
Or 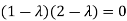
Or 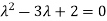
By Cayley-Hamilton theorem 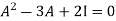
L.H.S: 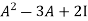
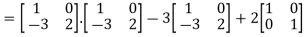
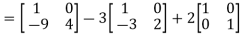
= 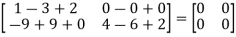 =0=R.H.S
=0=R.H.S
Multiply both side by 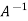 on
on 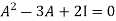
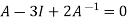
Or 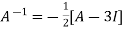
Or 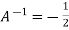 [
[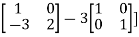
Or 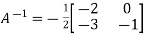
Example2: Verify the Cayley-Hamilton theorem and find the inverse.
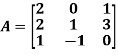
Sol. The characteristics equation of A is 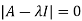
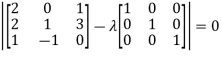
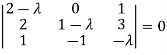
Or 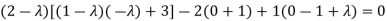
Or 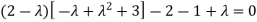
Or 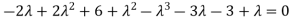
Or 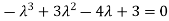
Or 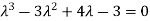
By Cayley-Hamilton theorem 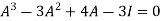
L.H.S. 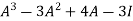
=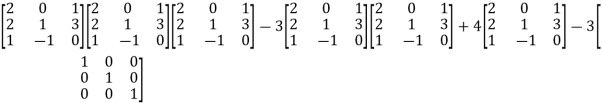
=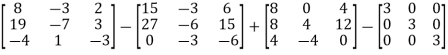
=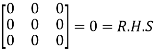
Multiply both side with 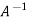 in
in 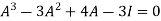
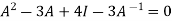
Or 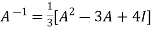
Or 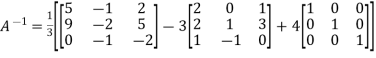
=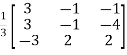
Example-3: Verify Cayley-Hamilton theorem for matrix A:
A = 
Sol. Characteristic equation of matrix A will be, 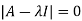
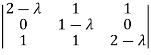 = 0
= 0
(2-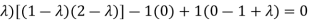
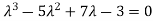
According to Cayley-Hamilton theorem,
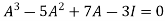 …………..(1)
…………..(1)
Here we need to verify eq.(1)-
First we will find A² -
A² = 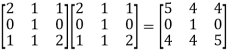
Now,
A³ = A².A = 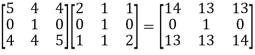
Equation (1) becomes,
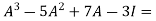
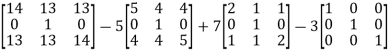
= 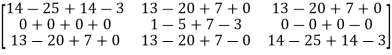
= 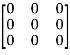
Hence the Cayley-Hamilton theorem is verified.
Example-4: Using Cayley-Hamilton theorem, find 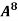 , if A =
, if A = 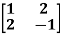 ?
?
Sol. Let A =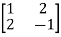
The characteristics equation of A is 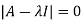
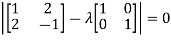
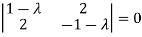
Or 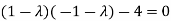
Or 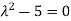
By Cayley-Hamilton theorem 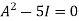
L.H.S. 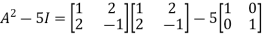
=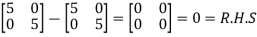
By Cayley-Hamilton theorem we have 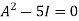
Multiply both side by 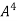
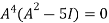 .
.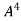
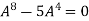
Or 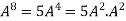
=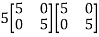
=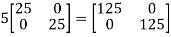
Suppose we have n matrices(vectors) - 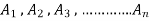
Then these matrices said to be dependent if-
1. All the rows or columns are of the same order.
2. n scalars 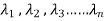 exists such as-
exists such as-
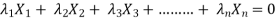
Otherwise they are linearly independent.
Example-1: Examine the following vectors to check whether they linearly dependent or independent and find the relationship if it exists.
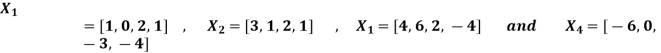
Sol. Let us consider the following matrix equation-
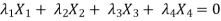 ………………..(1)
………………..(1)
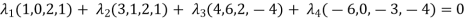
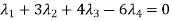
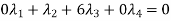
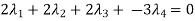
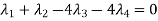
Matrix form of the above equations-
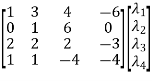 =
= 
Apply 
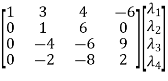 =
= 
Apply 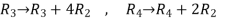
 =
= 
Apply 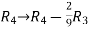
 =
= 
Now,
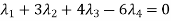
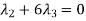
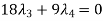
Suppose 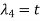 then
then
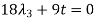
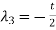
And, 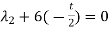
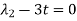
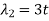
And, 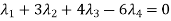
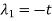
Put these values in equation (1), we get
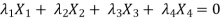
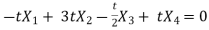
t is common here, so that
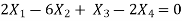
Linearly dependence and independence by rank method-
Working steps-
1. If the number of vectors are equal to the rank of the matrix, then vectors are linearly independent.
2. If the rank of the matrix of the given vectors is less than the number of vectors, then the vector are linearly dependent
Example: Check whether the set of vectors is linearly dependent or independent.
X = [1,2,-3,4] , Y = [3,-1,2,1] , Z = [1,-5,8,-7]
Sol. We have,
X = [1,2,-3,4] , Y = [3,-1,2,1] , Z = [1,-5,8,-7]
Write these vectors in matrix form,
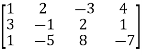
Apply 
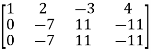
Apply 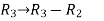
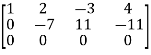
Rank of the matrix = 2 , which is less than the number of vectors.
Hence the vectors are linearly dependent.
Determinant test for linear dependence-
If the determinant of the given matrix(vectors) is zero, then we can say that the given matrix or vectors are linearly dependent.
Example: Check whether the vectors (3 , 1 , 6) , (2 , 0 , 4) and (2 , 1 , 4) are linearly dependent or independent.
Sol. Rows are the given vectors, so that we will find the value of its determinant, and if determinant is zero then we can conclude that, these vectors are linearly dependent.
 = 3( 0-4) - 1( 8-8) + 6( 2 – 0) = -12 – 0 + 12 = 0
= 3( 0-4) - 1( 8-8) + 6( 2 – 0) = -12 – 0 + 12 = 0
Since the value of determinant is zero, these vectors are linearly dependent.
Linear transformation-
Suppose that ‘A’ is a m× n matrix. Then a function f(x) = Ax is a linear transform of matrix A. Where f: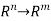 .
.
For examples,
Suppose we have a 2×3 matrix as below,
A = 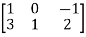 , now if we multiply this matrix with vector X = (x,y,z)
, now if we multiply this matrix with vector X = (x,y,z)
Then,
AX = 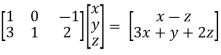 = (x – z ,
= (x – z , 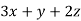 )
)
Example: suppose you have a matrix A = 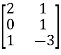 , then find the linear transformation of A.
, then find the linear transformation of A.
Sol. Here we have,
A = 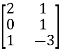
Multiply matrix A by vector (x,y).
X = (x,y)
Ax = 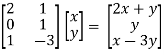
We get, f(x,y) = (2x + y , y , x – 3y)
Which is the linear transformation of matrix A.
Example: find the linear transformation of the matrix A.
A = 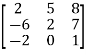
Sol. We have,
A = 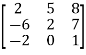
Multiply the matrix by vector x = (x , y , z) , we get
Ax = 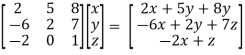
= (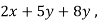
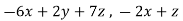 )
)
f(x , y , z) = (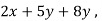
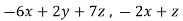 )
)
Which is the linear transformation of A.
Orthogonal transformation-
When a transformation from one set of rectangular coordinates to another set of rectangular coordinates, then this is called ‘orthogonal transformation’.
In other words-
A linear transformation Y = AX is said to be orthogonal, if matrix A is orthogonal that means,
AA’ = I = A’A
We have,
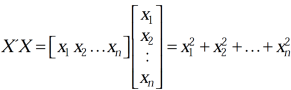
And similarly,
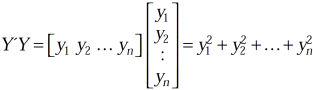
If Y = AX is an orthogonal transformation , then we have
X’X = Y’Y = (AX)’AX = X’A’ AX = X’(A’A)X
Which is only possible , if
A’A = I = AA’ and 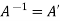
Therefore the square matrix A is said to be orthogonal if AA’ = A’A and 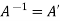
Example: Check whether the matrix A is orthogonal or not?
A = 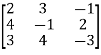
Sol. To check the orthogonality of this matrix , first we need to find AA’
So that,
AA’ = 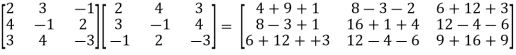
= 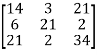
Here AA’ ≠ I
So , we can say that matrix A is not an orthogonal matrix.
Example: If the matrix A defines an orthogonal transformation , then show that
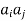 +
+ 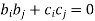 ( i≠j) i,j = 1 , 2 , 3.
( i≠j) i,j = 1 , 2 , 3.
Where A = 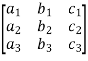
Sol. As we know that an orthogonal matrix A ,
AA’ = I = A’A and 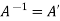
We will find AA’,
AA’ = 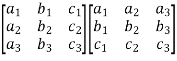 =
=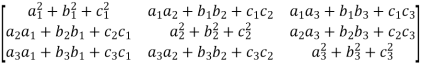
A will be orthogonal only if - AA’ = I
In that case, it is only possible when,
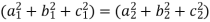 =
= 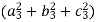 = 1
= 1
And,
(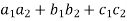 ) = (
) = (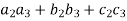 ) = (
) = (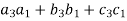 ) = 0
) = 0
NOTES-
1. The inverse and transpose of an orthogonal matrix is also orthogonal.
2. A linear transformation preserves length if and only if its matris is orthogonal.
3. The product of two or more than two orthogonal matrices is also orthogonal.
4. The determinant of an orthogonal matrix will always be ±1.