UNIT-1
MATRICES 1
A matrix is said to be of rank r when
1. It has at least one nonzero minor of order r,
2. Every minor of higher order than order r vanishes.
Equivalently the rank of a matrix is the largest order of any Non-vanishing minor of the matrix.
1. Elementary transformation n of a matrix:
2. The interchange of any two rows (columns).
3. The multiplication of any row (column) by a nonzero number.
The addition of a constant multiple of the elements of any row(column)to the corresponding elements of any other row(column).
Echelon form of a matrix:
The echelon form of a matrix consist of row echelon form and any matrix can be reduced into row echelon form with help of elementary transformation. The row echelon form consists of:
1. The first Non-zero in each row i.e. leading element is 1.
2. Each leading entry is in a column to the right of the leading entry of the previous row.
3. Rows with all zero elements, if any, are below to the rows with Non-zeros entries.
Example: 
Example1: Find the rank of the following matrix?
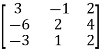
Sol.
Let A = 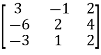
Applying 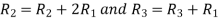
A 
Applying 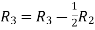
A 
Applying 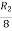
A 
Applying 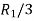
A 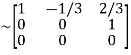
It is clear that minor of order 3 vanishes but minor of order 2 exists as 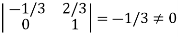
Hence rank of a given matrix A is 2 denoted by 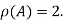
Example-2: Find the rank of the following matrix?

Sol.
Let A = 
Applying 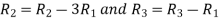

Applying 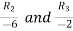
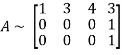
Applying 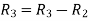
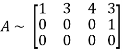
The minor of order 3 vanishes but minor of order 2 non zero as 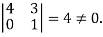
Hence the rank of matrix A is 2 denoted by 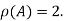
Example-3: Find the rank of the following matrix?

Sol.
Let A = 
Apply 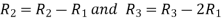

Apply 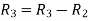

Apply 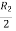
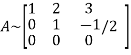
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as 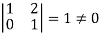
Hence the rank of given matrix is 2 i.e. 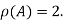
Rank of a matrix by triangular form-
This is the another method to find the matrix-
In this method, first we convert the matrix into its triangular form.
Then,
Rank = number of non-zero row in upper triangular matrix.
Example-4: Find the rank of the following matrix A-
A =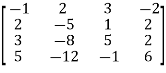
Sol. We have,
A =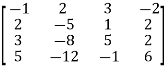
Apply 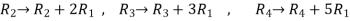
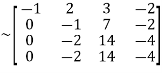
Apply 

In this matrix, 4th order and 3rd order minors are zero. But a minor of second order,
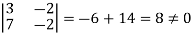
Hence,
Rank = number of non-zero rows = 2.
Example-5: Find the rank of the following matrix A by triangular form-
A =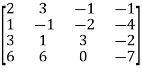
Sol. We have,
A =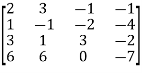
Apply 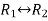
A =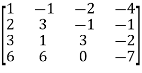
Apply 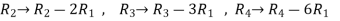
A =
Apply 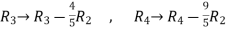
A =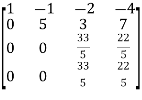
Apply 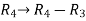
A =
Rank = number of non-zero rows.
Rank= 3.
Any non-zero matrix ‘A’ can be reduced to one of the following 4 forms by using elementary transformation-
1. 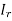
2. 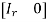
3. 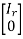
4. 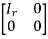
These forms are called the Normal form ( Canonical form) of ‘A’.
Here , the number of ‘r’ we get is called the rank of matrix ’A’.
The first canonical form of ‘A’ can be written as-
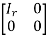
Example-1: Reduce the matrix ‘A’ to Normal form.
A =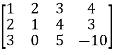
Sol. We have,
A =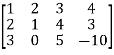
Apply 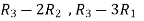
A = 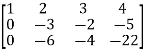
Apply 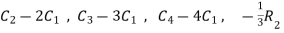 ,
, 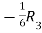 ,
, 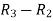
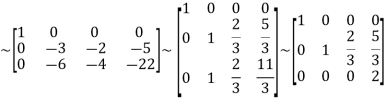
Apply 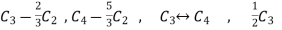

Which is the form of,
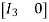 - this is the normal form of A.
- this is the normal form of A.
Example-2: Reduce the matrix ‘A’ to it’s normal form.
A = 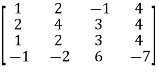
Sol. We have ,
A = 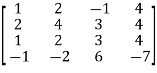
Apply 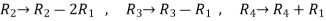
A = 
Apply 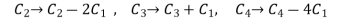
A = 
Apply interchange column-3 by column-2,
A = 
Apply 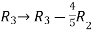 ,
, 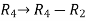
A = 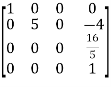
Apply 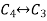
A = 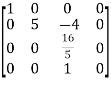
Apply 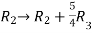 ,
, 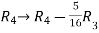
A = 
Apply 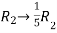 ,
, 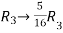
A = 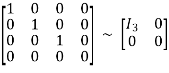
This is the normal form of matrix ‘A’.
There are two types of linear equations-
1. Consistent 2. Inconsistent
Let’s understand about these two types of linear equations
Consistent –
If a system of equations has one or more than one solution, it is said be consistent.
There could be unique solution or infinite solution.
For example-
A system of linear equations-
2x + 4y = 9
x + y = 5
Has unique solution,
Whereas,
A system of linear equations-
2x + y = 6
4x + 2y = 12
Has infinite solutions.
Inconsistent-
If a system of equations has no solution, then it is called inconsistent.
Consistency of a system of linear equations-
Suppose that a system of linear equations is given as-




This is the format as AX = B
Its augmented matrix is-
[A:B] = C
(1) consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n (no. Of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
(2) inconsistent equations-
If Rank of A ≠ Rank of C
Now we will understand how to solve the system of homogeneous and non-homogeneous linear equations.
Solution of homogeneous system of linear equations-
A system of linear equations of the form AX = O is said to be homogeneous, where A denotes the coefficients and of matrix and O denotes the null vector.
Suppose the system of homogeneous linear equations is,



It means,
AX = O
Which can be written in the form of matrix as below,
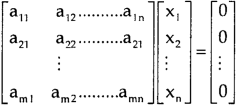
Note- A system of homogeneous linear equations always has a solution if
1. r(A) = n then there will be trivial solution, where n is the number of unknown,
2. r(A) < n , then there will be an infinite number of solution.
Example: Find the solution of the following homogeneous system of linear equations,
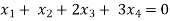
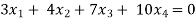
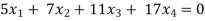
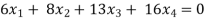
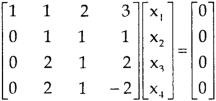
Sol. The given system of linear equations can be written in the form of matrix as follows,
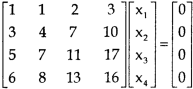
Apply the elementary row transformation,
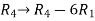 , we get,
, we get,
 , we get
, we get
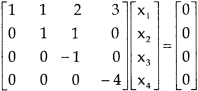
Here r(A) = 4, so that it has trivial solution,
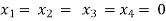
Example: Find out the value of ‘b’ in the system of homogeneous equations-
2x + y + 2z = 0
x + y + 3z = 0
4x + 3y + bz = 0
Which has
(1) trivial solution
(2) non-trivial solution
Sol. (1)
For trivial solution, we already know that the values of x , y and z will be zero, so that ‘b’ can have any value.
Now for non-trivial solution-
(2)
Convert the system of equations into matrix form-
AX = O
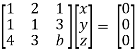
Apply 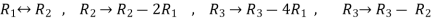 respectively , we get the following resultant matrices
respectively , we get the following resultant matrices
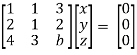
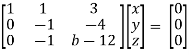
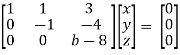
For non-trivial solutions, r(A) = 2 < n
b – 8 = 0
b = 8
Solution of non-homogeneous system of linear equations-
Suppose we have a system of linear equations-



The matrix form of the system of linear equations can be written as- AX = B

And,
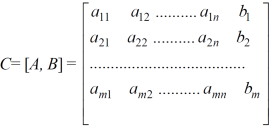
This is the augmented form matrix.
[ A:B] = C
Then
Consistent equation-
1. If Rank A = Rank C –
(a) Unique solution- Rank A = Rank C = n
(b) Infinite solution- Rank A = Rank C = r , r<n
Inconsistent equations-
If Rank A ≠ Rank C.
Example-1: check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
Sol. Write the above system of linear equations in augmented matrix form,
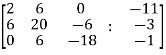
Apply 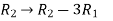 , we get
, we get
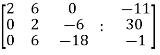
Apply 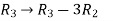
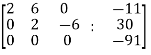
Here the rank of C is 3 and the rank of A is 2
Therefore both ranks are not equal. So that the given system of linear equations is not consistent.
Example: Check the consistency and find the values of x , y and z of the following system of linear equations.
2x + 3y + 4z = 11
X + 5y + 7z = 15
3x + 11y + 13z = 25
Sol. Re-write the system of equations in augmented matrix form.
C = [A,B]
That will be,
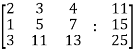
Apply 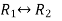
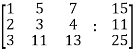
Now apply , 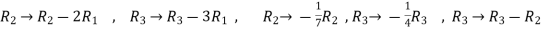
We get,
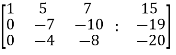 ~
~ 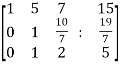 ~
~ 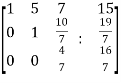
Here rank of A = 3
And rank of C = 3, so that the system of equations is consistent,
So that we can can solve the equations as below,
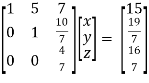
That gives,
x + 5y + 7z = 15 ……………..(1)
y + 10z/7 = 19/7 ………………(2)
4z/7 = 16/7 ………………….(3)
From eq. (3)
z = 4,
From 2,
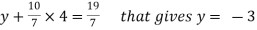
From eq.(1), we get
x + 5(-3) + 7(4) = 15
That gives,
x = 2
Therefore the values of x , y , z are 2 , -3 , 4 respectively.
Adjoint method to solve linear equations-
Suppose we have the system of linear equations –
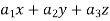 =
= 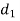
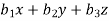 =
= 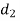
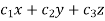 =
= 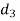
These equations can be written in the matrix form as-
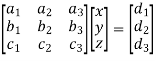
Or AX = B ………………….(1)
Where
A = 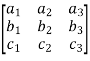 , X =
, X = 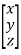 and B =
and B = 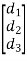
Multiply equation (1) by 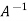 , we get
, we get
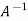 AX =
AX = 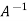 B or I X =
B or I X = 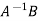 or
or
X = 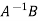
Example-1: Solve the system of linear equations-
x + y + z = 3
x + 2y + 2z = 4
x + 4y + 9z = 6
Sol. These eq. Can be written in the form of matrix,
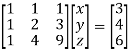
AX = B
Where, A = 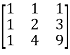 , X =
, X = 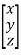 and B =
and B = 
Now we need to find out 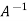
We know that ,
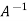 =
= 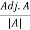
Matrix of co-factors = 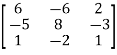
And
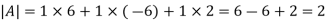
Then , 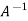 will be,
will be,
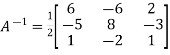
We know that,
X = 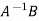
X = 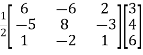
X = 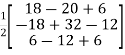 =
= 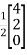 =
= 
So that,
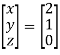
Here, x = 2 , y= 1 and z = 0.