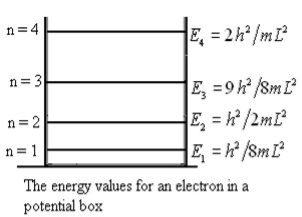
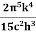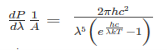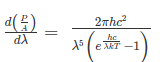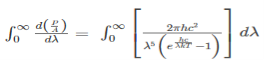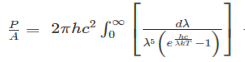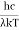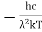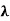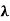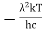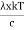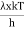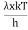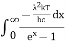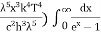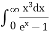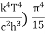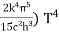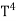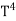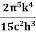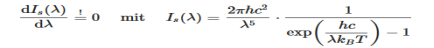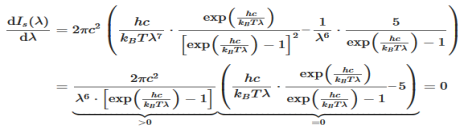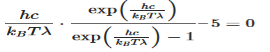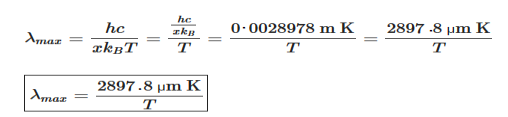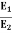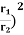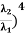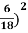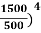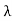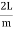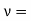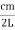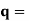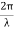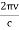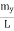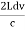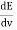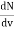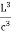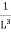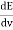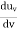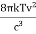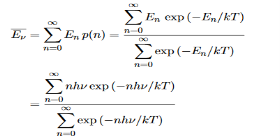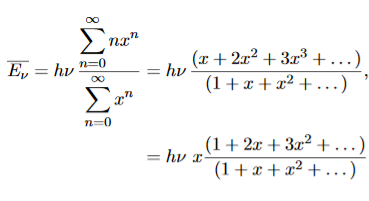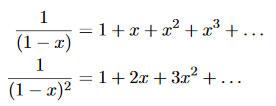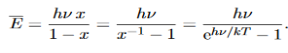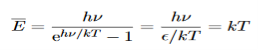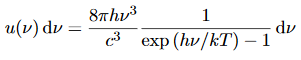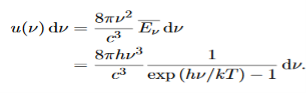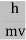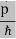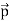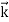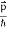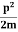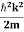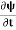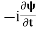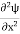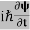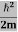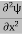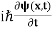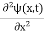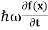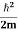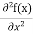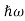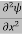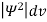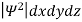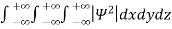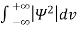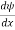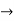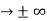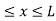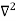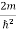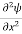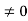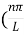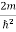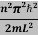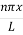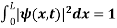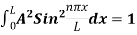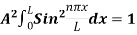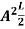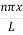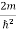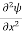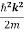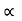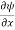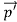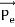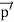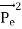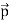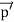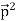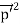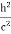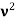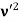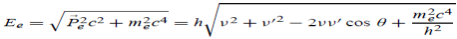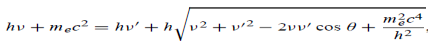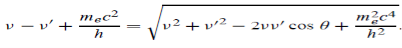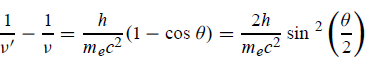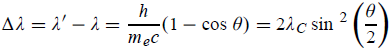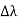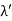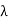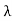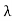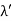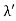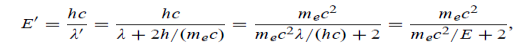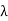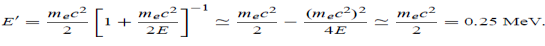Unit - 3
QUANTUM MECHANICS
A hot body emits thermal radiations which depend on composition and the temperature of the body. The ability of the body to radiate is closely related to its ability to absorb radiation.
A Body which is capable of absorbing almost all the radiations incident on it is called a black body.
A perfectly black-body can absorb the entire radiations incident on it. Platinum black and Lamp black can absorb almost all the radiations incident on them.
Emissive power of a black body:
It is defined as the total energy radiated per second from the unit surface area of a black body maintained at certain temperature.
Absorptive power of a black body:
It is defined as the ratio of the total energy absorbed by the black body to the amount of radiant energy incident on it in a given time interval. The absorptive power of a perfectly black body is 1.
One of the major ideas of quantum physics is quantization, measuring quantities in discrete, not continuous units.
The problem of black-body radiation one of the earliest challenges to classical physics.
When you heat an object, it begins to glow. Even before the glow is visible, it’s radiating in the infrared spectrum. The reason it glows is that as you heat it, the electrons on the surface of the material are agitated thermally, and electrons being accelerated and decelerated radiate light.
Physics in the late 19th and early 20th centuries was concerned with the spectrum of light being emitted by black bodies. A black body is a piece of material that radiates corresponding to its temperature — but most ordinary objects you think of as black, such as charcoal, also absorb and reflect light from their surroundings.
Well, it was hard to come up with a physical black body after all, what material absorbs light 100% and doesn’t reflect anything? But the physicists were clever about this, and they came up with the hollow cavity with a hole in it.
As discussed the blackbody is an idealization, because no physical object absorbs 100% of incident radiation, we can construct a close realization of a blackbody in the form of a small hole in the wall of a sealed enclosure known as a cavity radiator, as shown in Figure.
|
Figure: Black Body
The inside walls of a cavity radiator are rough and blackened so that any radiation that enters through a tiny hole in the cavity wall becomes trapped inside the cavity. At thermodynamic equilibrium (at temperature T), the cavity walls absorb exactly as much radiation as they emit. Furthermore, inside the cavity, the radiation entering the hole is balanced by the radiation leaving it. The emission spectrum of a blackbody can be obtained by analyzing the light radiating from the hole. Electromagnetic waves emitted by a blackbody are called blackbody radiation.
Spectral Distribution of energy in thermal radiation (Black Body radiation spectrum)
A good absorber of radiation is also a good emitter. Hence when a black body is heated it emits radiations. In practice a black body can be realized with the emission of Ultraviolet, Visible and infrared wavelengths on heating a body.
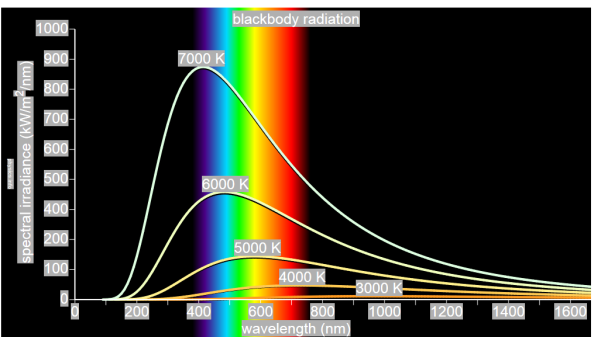
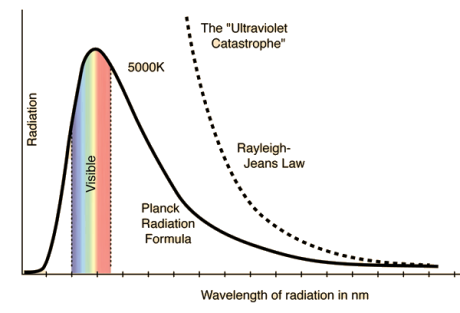
German physicists Lummer and Pringsheim studied the energy density as a function of wavelength for different temperatures of a black body using a spectrograph and a plot is made. This is called Black Body radiation spectrum.
|
You can see the spectrum of a black body (and attempts to model that spectrum) in the above figure, for different temperatures. one needs simply to analyse the spectral distribution of the radiation coming out of the hole. The radiation emitted by a blackbody when hot is called blackbody radiation.
The intensity I(λ,T) of blackbody radiation depends on the wavelength λ of the emitted radiation and on the temperature T of the blackbody.
The function I(λ,T) is the power intensity that is radiated per unit wavelength.
In other words, it is the power radiated per unit area of the hole in a cavity radiator per unit wavelength. According to this definition, I(λ,T)dλ is the power per unit area that is emitted in the wavelength interval from λ to λ+dλ.
The intensity distribution among wavelengths of radiation emitted by cavities was studied experimentally at the end of the nineteenth century. Generally, radiation emitted by materials only approximately follows the blackbody radiation curve. However, spectra of common stars do follow the blackbody radiation curve very closely.
Experimental data about blackbody radiation was obtained for various objects. Following results obtained,
- At equilibrium, the radiation emitted has a well-defined, continuous energy distribution.
- To each frequency there corresponds an energy density which depends neither on the chemical composition of the object nor on its shape, but only on the temperature of the cavity’s walls.
- The energy density shows a pronounced maximum at a given frequency, which increases with temperature; that is, the peak of the radiation spectrum occurs at a frequency that is proportional to the temperature. This is the underlying reason behind the change in colour of a heated object as its temperature increases, notably from red to yellow to white.
It turned out that the explanation of the blackbody spectrum was not so easy. The problem was that nobody was able to come up with a theoretical explanation for the spectrum of light generated by the black body. Everything classical physics could come up with went wrong.
The Stefan Boltzmann law describes the power radiated from a black body in terms of its temperature. Specifically, the Stefan Boltzmann law states that the total energy radiated per unit surface area of a black body across all wavelengths per unit time, is directly proportional to the fourth power of the black body's thermodynamic temperature T E is the total energy radiated per unit surface area T is the temperature of the object. e is the emissivity (how good of a radiator/absorber the object is). The emissivity e is a correction for an approximate black body radiator, where e = 1 – R, is the fraction of the light reflected (R) by the black body. For a true black body R = 0 and e = 1 or total absorption. Which is less than or equal to 1; in the case of a blackbody e =1. Derivation of Stefan Boltzmann Law The total power radiated per unit area over all wavelengths of a black body can be obtained by integrating Plank’s radiation formula. Thus, the radiated power per unit area as a function of wavelength is:
On simplifying Stefan Boltzmann equation, we get:
On integrating both the sides with respect to λ and applying the limits we get
The integrated power after separating the constants is:
This can be solves analytically by substituting: x = Therefore, dx= d Moreover h and c can also be written in terms of x as h = c = Substituting the above equation (3),(4),(5) and (6) in equation (2)
The above equation can be comparable to the standard form of integral:
So from equation (8) we can rewrite equation (7) as
On further simplifying we get, Thus, we arrive at a mathematical form of Stephen Boltzmann law: ⇒ E = σ Where, E = Where σ= So this is the mathematical derivation of Stefan’s Law. Example: A body of emissivity (e = 0.75), the surface area of 300 cm2 and temperature 227 ºC are kept in a room at temperature 27 ºC. Using the Stephens Boltzmann law, calculate the initial value of net power emitted by the body. Solution: E = P = eσA(T4 – T04) P = (0.75) (5.67 × 10-8 W/m2 – k4) (300 × 10-4 m2) × [(500 K)4 – (300 K)4] = 69.4 Watts. |
Wien’s law also called Wien’s displacement law. It is named after German physicist Wilhelm Wien, who received the Nobel Prize for Physics in 1911 for discovering the law. This law gives relationship between the temperature of a blackbody and the wavelength at which it emits the most light. Wien found that the radiative energy dW per wavelength interval dλ has a maximum at a certain wavelength λm and that the maximum shifts to shorter wavelengths as the temperature T is increased. He found that the product λmT is an absolute constant. Mathematical representation of the law: λmax =bT Where, b is the Wien’s displacement constant =2897.8 µm K T is the temperature in kelvins Wien’s constant: b (Wien’s displacement constant) Physical constant defining the relationship between the thermodynamic temperature of the black body and the wavelength is known as Wien’s constant. It is a product of temperature and wavelength of the black body which grows shorter as the wavelength reaches a maximum with temperature. The spectral distribution as a function of temperature is now to be examined more closely. It turns out that the maximum of the curve shifts with increasing temperature to ever shorter wavelengths. The dependence of this wavelength λmax. on the temperature is given by the following equation. This equation is also known as Wien’s displacement law. λmax. = 2897.8 µm K / T Wien’s displacement law
The Wien’s displacement law can be obtained by determining the maxima of Planck’s law. For this purpose, the function must be derived with respects to the wavelength λ. By using the product rule and setting the derivative equal to zero, we get
This equation will only be zero if the term in the round bracket becomes zero
This equation can only be solved numerically, e.g. with the Newton’s method. The result will be x = 4,9651. With this result the wavelength λmax can be determined as a function of the temperature by rearranging the equation.
The maximum of the spectral intensity can also be determined for the frequency form Is(f). For this the function Is(f) must be derived with respect to frequency f and setting the derivative equal to zero:
Example: A hot black body emits the energy at the rate of 16 J m-2 s-1 and its most intense radiation corresponds to 20,000 Å. When the temperature of this body is further increased and its most intense radiation corresponds to 10,000 Å, then find the value of energy radiated in Jm-2 s-1. Solution: Wein’s displacement law is, λm.T = b i.e. T so T1/T2 = λ2/λ1 so T1/T2 = 10,000/20,000 = 1/2 Here, λm becomes half, the Temperature doubles. Now from Stefan Boltzmann Law, e = sT4 e1/e2 = (T1/T2)4 ⇒ e2 = (T2/T1)4 . e1 = (2)4 . 16 = 16.16 = 256 J m-2 s-1
Example: Two spherical bodies A (radius 6 cm) and B (radius 18 cm) are at temperatures T1 and T2, respectively. The maximum intensity in the emission spectrum of A is at 500 nm and in that of B is at 1500 nm. Considering them to be black bodies, what will be the ratio of the rate of total energy radiated by A to that of B ?
Solution: Stefan-Boltzmann law gives the energy radiated per unit time by a spherical black body of area A=4πr2 and temperature T E=σAT4=4πσr2T4. The Wien's displacement law relates temperature of the black body to the wavelength at maximum intensity by λmT=b. Eliminate T from above equations to get, E=4πσb4(r2/λ4), which gives,
|
RAYLEIGH-JEANS LAW In his 1900 attempt, Rayleigh focused on understanding the nature of the electromagnetic radiation inside the cavity. He considered the radiation to consist of standing waves having a temperature T with nodes at the metallic surfaces. These standing waves, he argued, are equivalent to harmonic oscillators, for they result from the harmonic oscillations of a large number of electrical charges, electrons that are present in the walls of the cavity. When the cavity is in thermal equilibrium, the electromagnetic energy density inside the cavity is equal to the energy density of the charged particles in the walls of the cavity; the average total energy of the radiation leaving the cavity can be obtained by multiplying the average energy of the oscillators by the number of modes (standing waves) of the radiation in the frequency interval ν to ν +d ν.
The Rayleigh-Jeans Radiation Law was a useful, but this law is not completely successful attempt at establishing the functional form of the spectra of thermal radiation.
The energy density uν per unit frequency interval at a frequency ν is, according to the The Rayleigh-Jeans Radiation,
uν =8πν2kTc2 …………….(1)
Where k is Boltzmann's constant, T is the absolute temperature of the radiating body and c is the speed of light in a vacuum. This formula fits the empirical measurements for low frequencies, but fails increasingly for higher frequencies. The failure of the formula to match the new data was called the ultraviolet catastrophe. Derivation Consider a cube of edge length L in which radiation is being reflected and re-reflected off its walls. Standing waves occur for radiation of a wavelength λ only if an integral number of half-wave cycles fit into an interval in the cube. For radiation parallel to an edge of the cube this requires
Where m is an integer =
Between two end points there can be two standing waves, one for each polarization. In the following the matter of polarization will be ignored until the end of the analysis and there the number of waves will be doubled to take into account the matter of polarization. Since the frequency ν is equal to c/λ, where c is the speed of light
It is convenient to work with the quantity q, known as the wavenumber, which is defined as
and hence
In terms of the relationship for the cube, q =
and hence q2 = π2 (
Another convenient term is the radian frequency ω=2πν. From this it follows that q=ω/c. If mX, mY, mZ denote the integers for the three different directions in the cube then the condition for a standing wave in the cube is that q2 = π2 [(
This reduces to m2x + m2y + m2z =
Now the problem is to find the number of non-negative combinations of (mX, mY, mZ) that fit between a sphere of radius R and and one of radius R+dR. First the number of combinations ignoring the non-negativity requirement can be determined. The volume of a spherical shell of inner radius R and outer radius R+dR is given by dV=4πR2dR ……….(10) if R = then R = and hence dR = this means that dV = 4π(2Lν/c)2(2L/c) dν = 32π(L3v2/c3)dν ……….(14)
Now the non-negativity require for the combinations (mX, mY, mZ) must be taken into account. We know that the nonnegative combinations are in one quadrant of circle for the two dimensional case. The approximation arises from the matter of the combinations on the boundaries of the nonnegative quadrant. For the three dimensional case the nonnegative combinations constitute approximately one octant of the total. Thus the number dN for the nonnegative combinations of (mX, mY, mZ) in this volume is equal to (1/8)dV and hence dN = 4πv2dν ……….(15)
The average kinetic energy per degree of freedom is ½kT, where k is Boltzmann's constant. For harmonic oscillators there is an equality between kinetic and potential energy so the average energy per degree of freedom is kT. This means that the average radiation energy E per unit frequency is given by
and the average energy density, uν, is given by
The previous only considered one direction of polarization for the radiation. If the two directions of polarization are taken into account a factor of 2 must be included in the above formula; i.e.,
This is the Raleigh-Jeans Law of Radiation and holds empirically as the frequency goes to zero. The Rayleigh-Jeans Law was an important step in our understanding of the equilibrium radiation from a hot object, even though it turned out not to be an accurate description of nature. The careful work in developing the Rayleigh-Jeans law laid the foundation for the quantum understanding expressed in the Planck radiation formula. By Rayleigh-Jeans Law the energy density of radiation diverges at high frequencies. This is the famous result known as the ultraviolet catastrophe– the total energy in black-body radiation diverges. This expression for the spectral energy distribution of radiation is known as the Rayleigh-Jeans Law and, although it diverges at high frequencies, it is in excellent agreement with the measured spectrum at low frequencies and high temperatures.
Derivation of Planck’s law While Wien’s formula and the Rayleigh-Jeans Law could not explain the spectrum of a black body, Max Planck’s equation solved the problem by assuming that light was discrete. The photoelectric effect demonstrates that light waves have particle properties and that the light quanta or photons of a particular frequency v each have energy hv. We need to reconcile this picture with the classical picture of electromagnetic waves in a box. In the classical picture, the energy associated with the waves is stored in the oscillating electric and magnetic fields. We found it necessary to impose the constraint that only certain modes are permitted by the boundary conditions; the waves are constrained to fit into the box with whole numbers of half wavelengths in the x, y, z directions. Now we have a further constraint. The quantisation of electromagnetic radiation means that the energy of a particular mode of frequency v cannot have any arbitrary value but only those energies which are multiples of hν, in other words the energy of the mode is E(ν) =nhv, where we associate n photons with this mode. We now consider all the modes (and photons) to be in thermal equilibrium at temperature T. In order to establish equilibrium, there must be ways of exchanging energy between the modes (and photons) and this can occur through interactions with any particles or oscillators within the volume or with the walls of the enclosure. We now use the Boltzmann distribution to deter-mine the expected occupancy of the modes in thermal equilibrium. The probability that a single mode has energy En=nhv is given by the usual Boltzmann factor Where the denominator ensures that the total probability is unity, the usual normalisation procedure. In the language of photons, this is the probability that the state contains n photons of frequency ν. The mean energy of the mode of frequency ν is therefore
……….(20) To simplify the calculation, let us substitute x=exp(−hν/kT). Then (20) becomes
Now, we remember the following series expansions:
Hence, the mean energy of the mode is
This is the result we have been seeking. To find the classical limit, we allow the energy quanta hν to tend to zero. Expanding ehν/kT−1 for small values of hν/kT, ehν/kT−1 = 1 +hν/kT+ Thus, for small values of hν/kT, ehν/kT−1 =hν/kT. And also
Thus, if we take the classical limit, we recover exactly the expression for the average energy of a harmonic oscillator in thermal equilibrium, We have already shown that the number of modes in the frequency interval ν to ν+dν is (8πν2/c3) dν per unit volume. The Planck distribution in terms of the energy density of radiation per unit frequency interval
The energy density of radiation in this frequency range is
This is the Planck distribution function. |
As we know in the Photoelectric Effect, the Compton Effect, and the pair production effect—radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal.
In 1923, the French physicist Louis Victor de Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
All material particles should also display dual wave–particle behaviour. That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p = hν/c = h/λ. We can generalize this relation to any material particle with nonzero rest mass. Each material particle of momentum
λ =
Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation. λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment.
However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c. Therefore
Example: What is the frequency of a photon with energy of 4.5 eV? Solution: E = (4.5 eV) x (1.60 x 10-19 J/eV) = 7.2 x 10-19 J E = hf
h = 6.63 x 10-34 J x s |
De Broglie’s Hypothesis: Matter Waves Matter waves: According to De-Broglie, a wave is associated with each moving particle which is called matter waves.
As we know in the photoelectric effect, the Compton Effect, and the pair production effect radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal: all material particles should also display a dual wave–particle behaviour.
That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p = h ν /c = h/λ, we can generalize this relation to any material particle with nonzero rest mass: each material particle of momentum λ = Wave has wavelength λ here h is Planck's constant and p is the momentum of the moving particle. We have seen that microscopic particles, such as electrons, display wave behaviour. What about macroscopic objects? Do they also display wave features? They surely do. Although macro-scopic material particles display wave properties, the corresponding wavelengths are too small to detect; being very massive, macroscopic objects have extremely small wavelengths.
At the microscopic level, however, the waves associated with material particles are of the same size or exceed the size of the system. Microscopic particles therefore exhibit clearly noticeable wave-like aspects. The general rule is: whenever the de Broglie wavelength of an object is in the range of, or exceeds, its size, the wave nature of the object is detectable and hence cannot be neglected. But if its de Broglie wavelength is much too small compared to its size, the wave behaviour of this object is undetectable.
For a quantitative illustration of this general rule, let us calculate in the following example the wavelengths corresponding to two particles, one microscopic (electron) and the other macroscopic(ball).
Example: What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s? Solution: (a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s) p = 4.92 × 10–24 kg m/s de Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s λ= 0.135 nm (b)For the ball: Mass m’ = 0.150 kg, Speed v ’= 30.0 m/s. Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s) p’= 4.50 kg m/s de Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement. |
Characteristics of Matter waves:
Matter waves are the waves associated with matter in motion. Wavelength of the matter waves is given by λ=h/p.
- Matter waves are not progressive waves. They are localized waves.
- Matter waves are not single waves. They are group of waves (wave packet) assumed formed due to the superposition of two or more progressive waves.
- Matter waves called pilot waves and they represent the direction of propagation of matter.
- Unlike electromagnetic waves, matter waves will not have constant speed. The speed of matter waves depends on the mass of the particle.
- Vg x Vp=C2 shows that Vp, phase velocity of matter waves is greater than velocity of light. This shows that matter waves not physical waves
- Lighter the particle, greater is the De-Broglie wave length.
- The faster the particle moves, the smaller is its De-Broglie wave length.
- The De-Broglie wave length of a particle in independent of the charge or nature of the particle.
- The matter waves are not electromagnetic in nature. The electromagnetic waves are produced only by charged particle.
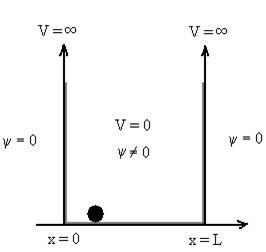
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory. Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x. So We have E= K+V =
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk. Using this equation (1) for the energy will become ℏω =
A wave with frequency ω and wave number k can be written as usual as ψ(x, t) =Aei(kx−ωt) ……….. (3)
the above equation is for one dimensional and for three dimensional we can write it as ψ(r, t) =Aei(k·r−ωt) ……….. (4) But here we will stick to one dimension only.
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain ℏ(ωψ) = This is the time-dependent Schrodinger equation. If we put the x and t in above equation then equation (7) takes the form as given below
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
We already know that E=
Eψ = -
This is called the time-independent Schrodinger equation. |
It is not possible to measure all properties of a quantum system precisely. Max Born suggested that the wave function was related to the probability that an observable has a specific value. In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2’. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’ . Thus Ψ2 is a measure of particle density. According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume( dv=dxdydz) is given by
Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space. i.e
Or This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function. The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as ψ(x, y, z, t) = a + ib and its complex conjugate as ψ*(x, y, z, t) = a – ib. The product of wave function and its complex conjugate is ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2 a2 + b2 is a real quantity.
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
Only wave function with all these properties can yield physically meaningful result. Physical significance of wave function
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation. All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics. |
In his 1923 experiment, Compton provided the most conclusive confirmation of the particle aspect of radiation.
By scattering X-rays off free electrons, he found that the wavelength of the scattered radiation is larger than the wavelength of the incident radiation. This can be explained only by assuming that the X-ray photons behave like particles.
According to classical physics, the incident and scattered radiation should have the same wavelength.
Also we know that the energy of the X-ray radiation is too high to be absorbed by a free electron therefore the incident X-ray would then provide an oscillatory electric field which sets the electron into oscillatory motion, hence making it radiate light with the same wavelength but with an intensity I that depends on the intensity of the incident radiation I0
But neither of these two predictions of classical physics is compatible with experiment.
|
Figure: Elastic scattering of a photon from a free electron
By experiment Compton reveal that the wavelength of the scattered X-radiation increases by an amount 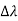 , called the wavelength shift, and that
, called the wavelength shift, and that 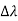 depends not on the intensity of the incident radiation, but only on the scattering angle.
depends not on the intensity of the incident radiation, but only on the scattering angle.
Compton succeeded in explaining his experimental results only after treating the incident radiation as a stream of particles—photons—colliding elastically with individual electrons.
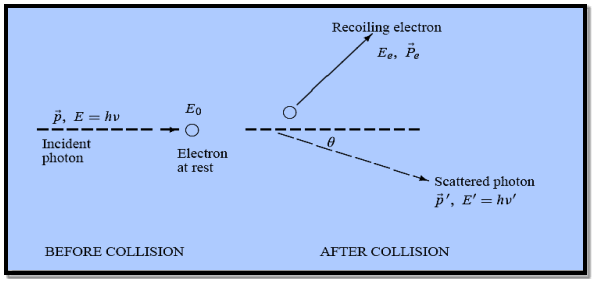
Here we will discuss elastic scattering of a photon from a free electron as shown in figure. Consider that the incident photon, of energy E =hν and momentum p = hν /c, collides with an electron that is initially at rest. If the photon scatters with a momentum
Which leads
Energy Conservation The energies of the electron before and after the collision are given, respectively, by E0 =mec2 ………..(3)
Since the energies of the incident and scattered photons are given by E = hν and E0 = hν’, respectively, conservation of energy dictates that E + E0 = E’ + Ee ………..(4)
Which leads to
Squaring both sides of (5) and simplifying, we get
Hence wavelength shift is given by
Where λC = h/mec = 2.426 x 10-12 m is called the Compton wavelength of the electron.
This relation connects the initial and final wavelengths to the scattering angle. |
Compton’s experimental observation:
- The wavelength shift of the X-rays depends only on the angle at which they are scattered and not on the frequency (or wavelength) of the incident photons.
- The Compton Effect confirms that photons behave like particles. They collide with electrons like material particles.
Example: High energy photons are scattered from electrons initially at rest. Assume the photons are back scattered and their energies are much larger than the electron’s rest-mass energy, E = mec2. (a) Calculate the wavelength shift. (b) Show that the energy of the scattered photons is half the rest mass energy of the electron, regardless of the energy of the incident photons. (c) Calculate the electron’s recoil kinetic energy if the energy of the incident photons is 150 MeV.
Solution: (a) In the case where the photons backscatter i.e. θ = π The wavelength shift becomes
(b) Since the energy of the scattered photons E’ is related to the wavelength
Where E = hc/
(c) If E = 150 MeV, the kinetic energy of the recoiling electrons can be obtained from conservation of energy Ke = E – E’
Example: X-rays with an energy of 300 keV undergo Compton scattering with a target. If the scattered X-rays are detected at 30° relative to the incident X-rays, determine the Compton shift at this angle, the energy of the scattered X-ray, and the energy of the recoiling electron. Solution: The Compton shift When it is scattered through an angle θ by an electron: λ′−λ= λe(1−cosθ) We know Compton wavelength of the electron λe= h/mec= 2.43 pm me mass of the electron = 511 keV/c2 θ = 30° Compton shift is λ′−λ= λe(1−cosθ) = 2.426 x 10-12 m (1−cos30◦.) = 0.325 pm The energy E′ of the scattered photon is E′=hc/ λ′ And λ=hc/E E=300 keV is the wavelength of the incoming photon. It follows that E′= 278 keV. By conservation of energy, the energy lost by the photon in the collision is converted into kinetic energy K of the recoiling electrons K= 22 keV |
Reference Books
1. Concepts of Modern Physics - AurthurBeiser (Mc-Graw Hill)
2. Introduction to Special Theory of Relativity- Robert Resnick (Wiley)
3. Optics - Brijlal& Subramanian (S. Chand )
4. Engineering Physics: Theory and Practical- Katiyar and Pandey (Wiley India)
5. Applied Physics for Engineers- Neeraj Mehta (PHI Learning, New)
6. Engineering Physics-Malik HK and Singh AK (McGrawHill)